基于高精度轨迹数据的车辆换道行为识别研究

徐文洁 赵 欣 酆 磊 陈 曦

(武汉理工大学交通与物流工程学院 武汉 430063)

0 引 言

换道与跟驰是驾驶人在道路交通环境中最基本的驾驶行为,随着大数据技术应用的兴起,基于车辆出行微观轨迹点数据的换道行为识别研究逐渐成为交通领域研究热点之一.

微观轨迹数据的采集方法有很多,如车载设备定时记录车辆GPS轨迹坐标.康军等[1]通过大规模的西安市出租车GPS轨迹数据挖掘城市出租车司机换道行为特征,设计了换道行为识别支持向量机模型.孙超等[2]提出了基于海量秒级GPS轨迹数据的驾驶行为评价方法,给出了超速、急变速、频繁换道等行为的判定方法和阈值.

也有部分研究通过模拟驾驶器进行模拟驾驶试验获得车辆轨迹数据,黑凯先等[3]基于车辆多自由度驾驶仿真平台,采集车辆运行状态参数的相关数据,在不同维度的特征集和多个样本时窗状况下,运用随机森林决策树方法连续识别驾驶员的换道行为.Dogan等[4]基于驾驶模拟试验数据,分别构建了前馈神经网络、递归神经网络和支持向量机三种换道识别模型,通过对比分析发现支持向量机识别效果更理想.

以上轨迹数据提取方法,基于GPS车辆定位的轨迹数据精度不足,记载时间间隔相对较长造成数据离散,调用数据量大,计算和渲染轨迹时间长;基于模拟仿真平台的驾驶试验始终处于虚拟的驾驶环境中,驾驶数据的真实性、可靠性程度无法与实车试验比拟.这些缺点导致得到的车辆行驶轨迹不准确,无法用于精准分析驾驶人换道行为.文中依托高精度定位技术的BDS北斗卫星导航系统,其定位精度可分为dm、cm级别,测速精度0.2 m/s,授时精度10 ns,为名副其实的车道级定位,能有效的辅助道路交通领域的科学研究.本次研究的数据采样频率选定为10 Hz.

1 换道行为识别模型

1.1 基本参数定义与计算

图1为车辆行驶微观轨迹点任意两点之间的方位角α示意图,以正北为起点,顺时针为正,0°≤α≤360°.

图1 方位角示意图

地球上任何区域任意两点的普适的求方位角的方法如下[5].

已知地球球面上两点A,B的经纬度,A为当前位置,B为目标位置,求B点相对于A点的方位角,引入任意一点C:

cos (C)=cos(90°-Bw)×cos (90°-Aw)+

sin (90°-Bw)×sin (90°-Aw)×cos (Bj-Aj)

(1)

(2)

(3)

式中:Aw,Aj,Bw,Bj分别为A点的纬度,A点的经度,B点的纬度,B点的经度.北纬为正,南纬为负;东经为正,西经为负.

假设A点固定为原点,B点相对于A点的位置在四个象限上进行讨论(本文不讨论B相对于A的位置在两个坐标轴上),B相对A的方位角α计算公式见表1.

表1 方位角计算方法

每个时间粒度点均有角速度,这里将相邻时间粒度点的方位角变化率作为其角速度,轨迹点j的角速度公式为

(4)

由图1可知:ΔT为数据采集的时间粒度,即0.1 s.

地球上任意两点A,B的距离为

dA,B=2arcsin[sin((Bw-Aw)/2)2+cosAw×

(5)

式中:Aw,Aj,Bw,Bj分别为A点的纬度,A点的经度,B点的纬度,B点的经度;R为地球半径,6 371 km.

1.2 初始坐标系建立

车辆在某直线路段上行驶,从路段最左截面开始进行轨迹点数据记录,以时间为X轴,横向位置为Y轴,以最左截面与最下车道的交点为原点,建立平面坐标系.车辆进入路段最左截面的点记为截面入口点,车辆离开路段最右截面的点记为截面出口点.图2中α0为截面入口点相对于原点的方位角,α为任意轨迹点相对于原点的方位角.车辆行进方向相对于大地坐标系的正北方向可能存在图2中的四种情形.本文主要以第一种情形为研究对象,其余情形只需改变任意轨迹点与原点连线相对于Y轴的夹角的表达式再带入横向偏移距离计算公式即可.

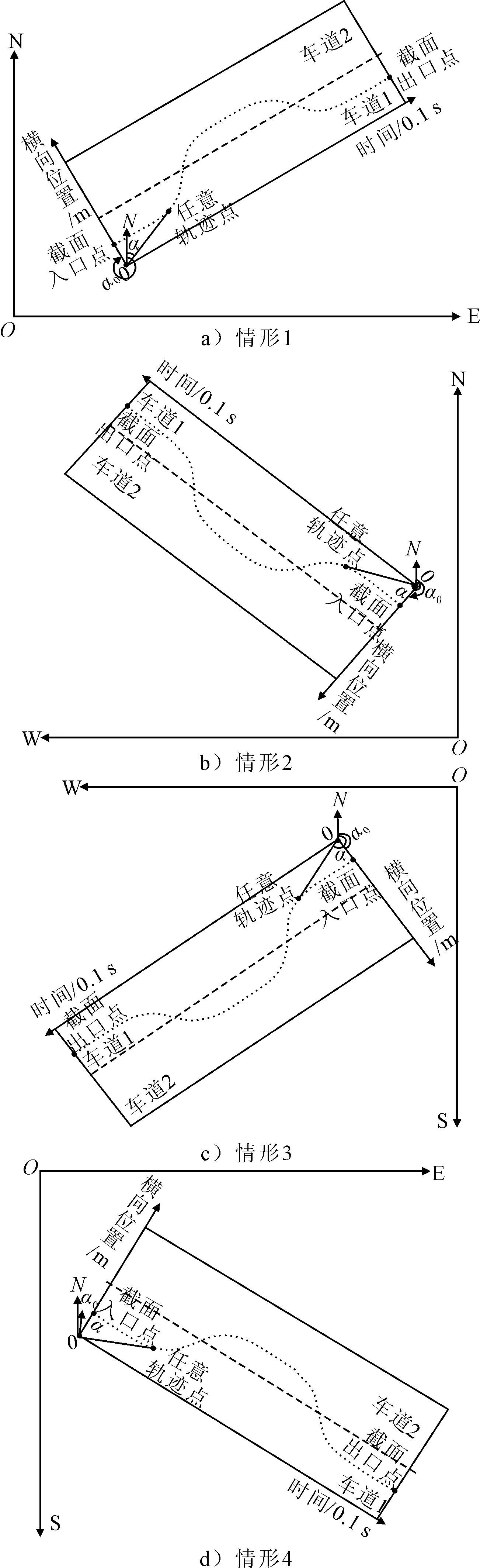
图2 车辆四种行进方向

1.3 车辆换道分阶段

文献[6]将车辆换道分为换道决策阶段和换道执行阶段.将换道执行阶段定义为车辆发生单向连续横向偏移的持续时间段.其研究中统计了537辆车的换道执行阶段持续时间的分布状况,见表2.

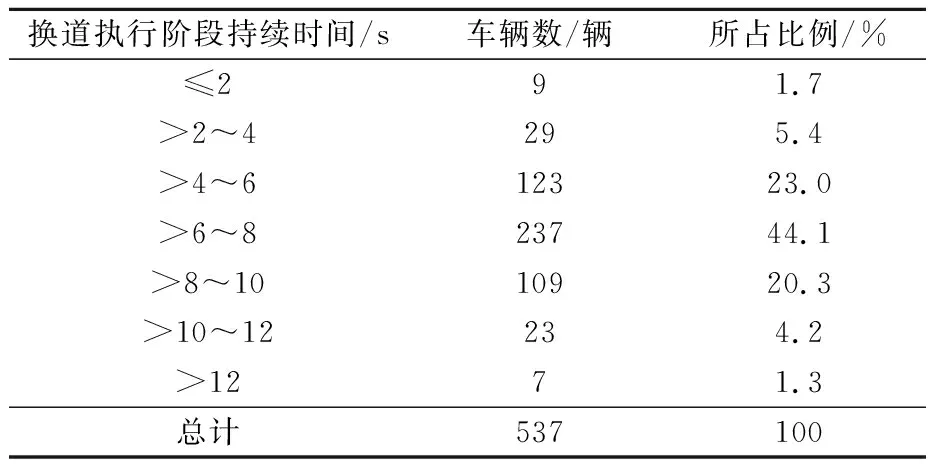
表2 换道执行阶段持续时间分布状况

将换道执行阶段划分为两个子阶段:换道开始阶段、换道结束阶段.取置信水平为95%,换道执行阶段持续时间的置信区间取整为[2,12].

车辆换道执行阶段两子阶段的横向位移轨迹近似S形,定义换道开始阶段轨迹点角速度开始连续为正(或连续为负)的第一点为换道开始时刻点St,定义换道结束阶段轨迹点角速度开始连续为负(或连续为正)的最后一点为换道结束时刻Ft,定义车辆微观轨迹点角速度为0,其左右邻域内轨迹点的角速度正负相反的时间粒度点为换道时刻点Mt,见图3,换道开始阶段、换道结束阶段具体表现为:

图3 车辆换道各阶段示意图

1) 换道开始阶段 在具备换道条件后,车辆开始执行换道,从车辆向左(或向右)打转向盘到微观轨迹点连续横向移动到换道时刻点.在这一阶段,理想状态下,车辆微观轨迹点应具有相同方向的角速度.

2) 换道结束阶段 即为车辆开始向右(或向左)回转向盘至安全完成换道,开始进入跟驰前车状态.在这一阶段,车辆微观轨迹点继续横向移动到换道结束时刻点,车辆微观轨迹点应具有相同方向的角速度并与前一阶段的角速度方向相反.

设备采集数据受驾驶员操作特性、设备本身的稳定性等诸多因素影响,实际换道微观轨迹点的数据不可避免地存在异常值和测量误差,两阶段的角速度不可能全部为正值或全部为负值.对多次换道试验数据进行统计对比分析得出,换道开始阶段或换道结束阶段有50%以上的轨迹点的角速度方向一致,为正或为负,且分布较为均匀.

1.4 临界点标定

1) 换道时刻点Mt的标定 换道时刻点Mt理论上应为角速度为0的时刻点[7].由于本研究是基于工作频率为10 Hz的定位系统下所得到的轨迹数据,其获取到的轨迹数据并不是连续的而是时间粒度为0.1 s的离散数据,在搜索过程中可能无法找到角速度为0的点,考虑到该点左右相邻点角速度方向必定一正一负,以其左右相邻点中角速度最接近0的轨迹点替代该点.利用式(4)计算每个轨迹点j的角速度ω(tj) ,定义:

(6)

计算各轨迹点的G(tj),搜索G(tj-0.1)×G(tj+0.1)=-1且|ω(tj)|≤min{|ω(tj-0.1)|,|ω(tj+0.1)|}的点,即为换道时刻点的替代点,记为jd1,jd2,…,jdN,各点对应的时刻记为tjd1,tjd2,…,tjdN,将一次出行的轨迹数据分为[tjd1-6,tjd1+6],[tjd2-6,tjd2+6],…,[tjdN-6,tjdN+6]N段,作为后续研究的搜索区间.

2) 换道开始时刻点St及换道结束时刻点Ft的标定 换道开始阶段必须有50%以上的轨迹点的角速度方向一致,为正(或为负),且分布较为均匀.在本研究中,定义了换道开始阶段最长持续时间为6 s,最短持续时间为1 s.数据采集频率为10 Hz,1 s为一个判断时段,每秒10个微观轨迹点中至少存在六个角速度为正(或为负)的轨迹点,至多有4个角速度为负(或为正)的轨迹点,故1 s内∑G(t)≥2(或∑G(t)≤-2),换道结束阶段同理.按照前文确定的换道时刻点jd1,jd2,…,jdN及搜索区间[tjd1-6,tjd1+6],[tjd2-6,tjd2+6],…,[tjdN-6,tjdN+6],依次对各个搜索区间进行搜索,寻找每个搜索区间的换道开始时刻点St及换道结束时刻点Ft.

1.5 横向偏移距离

1) 换道横向偏移距离范围 车辆完成一次变道产生的横向偏移距离与车辆横向安全距离相关,车辆横向安全距离表示两车并行时的最小横向安全间距,由车辆实时速度确定,为

dsafe(v)=a+b×vc

(7)

式中:a取0.6;b取0.06;c取0.5.

假定在交通量饱和的道路上,车辆正常行驶在车道中心位置,车道宽度为H0,车辆宽度为D,车辆到车道线的安全距离为h0,那么

2h0=dsafe(v)

(8)

可以推算得到车辆到车道线的安全距离随车辆速度变化函数:

h0(v)=0.5a+0.5b×(v)c

(9)

见图4.

图4 车辆换道横向偏移范围

车辆安全换道最大的横向偏移距离为

xmax(v)=2H0-2h0(v)-D

(10)

车辆安全换道最小的横向偏移距离为

xmin(v)=2h0(v)+D

(11)

2) 车辆实际横向偏移距离 车辆截面入口点与原点连线相对于正北方向的方位角α0,换道开始时刻最早点tjdn-i与原点连线相对于正北方向的方位角αSt及距离d0,St,换道结束时刻最晚点tjdn+i与原点连线相对于正北方向的方位角αFt及距离d0,Ft.则该段换道轨迹最大横向偏移距离为

Xmax=|d0,Ft×cos(αFt+360°-α0)-

d0,St×cos(αSt+360°-α0)|=

|d0,Ft×cos(αFt-α0)-d0,St×cos(αSt-α0)|

(12)

(13)

见图5.

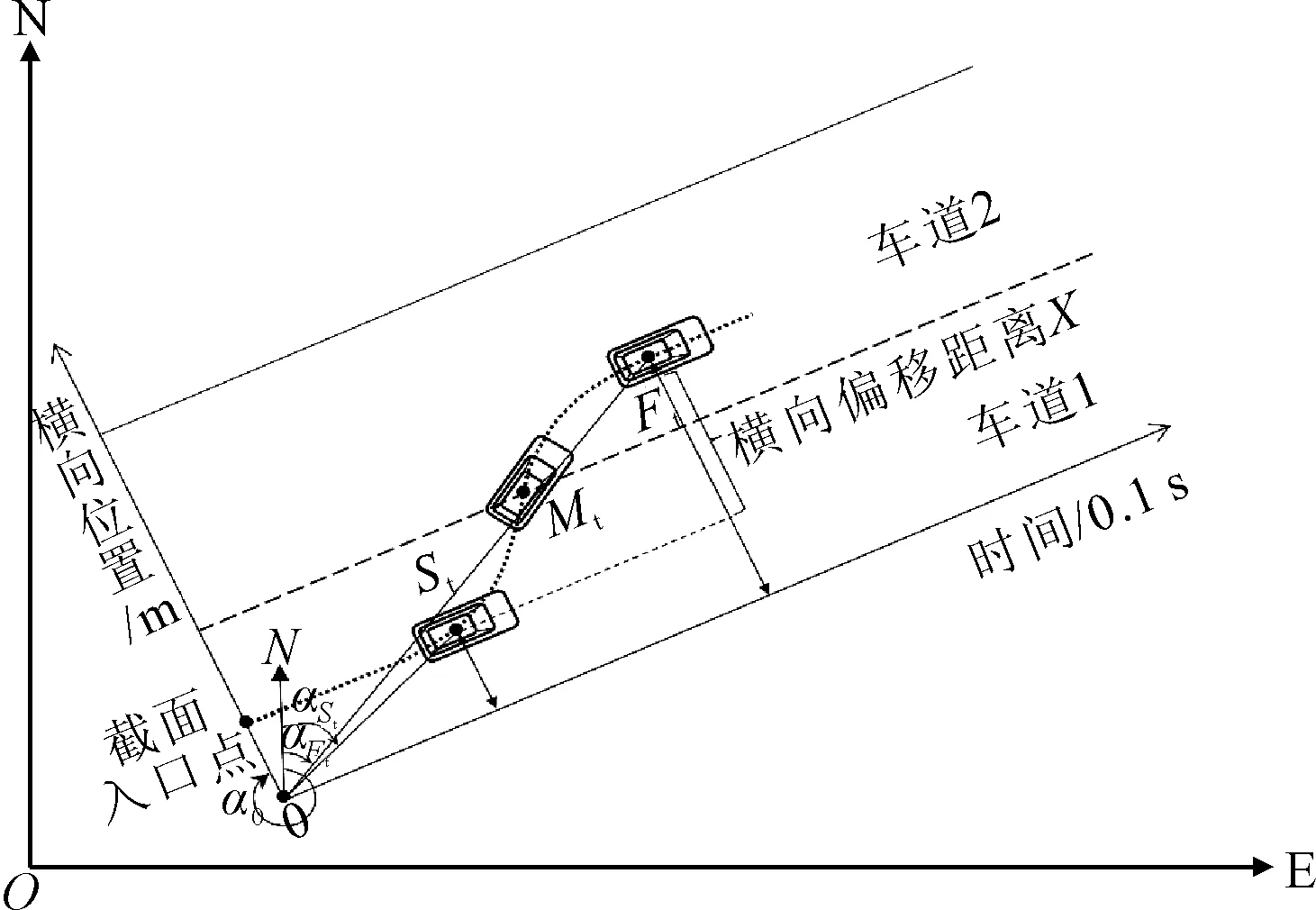
图5 车辆换道横向偏移距离

3) 车辆换道安全横向偏移距离X∈(xmin(v),xmax(v))与车辆实际横向偏移距离比较,若满足:

Xmin≥xmin(v)

Xmax≤xmax(v)

(14)

则表示该段轨迹为一次安全换道行为.

1.6 算法流程图

在进行临界点的搜索后,可初步标定出换道时刻点Mt、换道开始时刻点St、换道结束时刻点Ft,此时仍然无法有效区分换道行为与车辆在一条车道上S形波动,因此添加1.5换道横向偏移距离这一约束条件,最终可得到每次出行车辆发生换道行为的次数、车辆的行驶速度、每次换道持续时间范围、每次换道横向偏移距离范围.算法流程图见图6.

图6 车辆换道识别算法流程图

2 案例分析

2.1 试验说明

实车试验地点为武汉市临江大道某路段,全线为直线段,共4.8 km.选取40名驾龄各异(取整)的驾驶员,依据驾龄从小到大的顺序将其编号为1～40,驾驶时车载平板自动采集高精度定位数据并实时传送到服务器后台.

2.2 数据获取及预处理

基础数据为实测的出行轨迹点经纬度坐标数据,算法运行前,首先将原始经纬度数据转化为标准格式,还须对标准格式数据进行以下几个方面处理:①错误数据处理,将超出武汉市经纬度范围(东经113°41′～115°05′、北纬29°58′～31°22′)的数据判定为错误数据,予以剔除;②缺失数据处理,对于连续时间点中存在部分坐标数据缺失的情况,利用插值法结合上下坐标数据进行补齐,当存在大段坐标数据缺失的情况,弃用该条出行轨迹数据[8].

2.3 试验结果及分析

1) 试验结果 将清洗后的数据输入至换道识别模型中,模型可输出每位驾驶员一次出行的换道次数、行驶速度、每次换道的持续时间范围、每次换道的横向偏移距离范围.对模型的输出结果进行二次处理,统计出每位驾驶员在同一直线路段上一次出行的换道次数、行驶速度、平均换道持续时间、平均换道横向偏移距离,并附上每位驾驶员的编号和驾龄,见表4.

表4 换道行为识别结果统计表

2) 试验结论分析 为观察试验数据分布特征规律,利用spss统计分析软件进行层次聚类分析,将驾驶员换道次数、行驶速度作为变量,将驾驶员编号作为聚类样本,按照变量对不同编号的驾驶员进行Q型聚类,见表5,将40名驾驶员分为两组.

表5 层次聚类分布情况

图7为1组、2组的驾驶员换道次数分布图和驾驶员行驶速度分布图.

由图7可知:归为1组的驾驶员的换道次数与行驶速度大部分高于平均值,归为2组的驾驶员行驶速度与换道次数大部分低于平均值.从驾驶员编号分布上看,换道次数分布图和行驶速度分布图存在相似特征,即1组的分布较为居中,代表1组成员的驾龄属于中间层,2组的分布两侧成员较集中,代表驾龄分布在低层级和高层级的成员较为集中.因此结合以上特征,进行如下定义:将1组的驾驶员的驾驶行为定义为活跃类型,这类驾驶员有一定的驾驶经验,在路段上行驶时通过频繁变换车道以提升行驶速度,因此换道次数及行驶速度都相对较高.将2组的驾驶员的驾驶行为定义为稳重类型,这类驾驶员在路段上行车稳重,多处于跟驰状态,主动换道行为较少,行驶速度相对不高,多为驾驶经验不足、行车谨慎和有多年驾驶经验、操作平稳的人群.

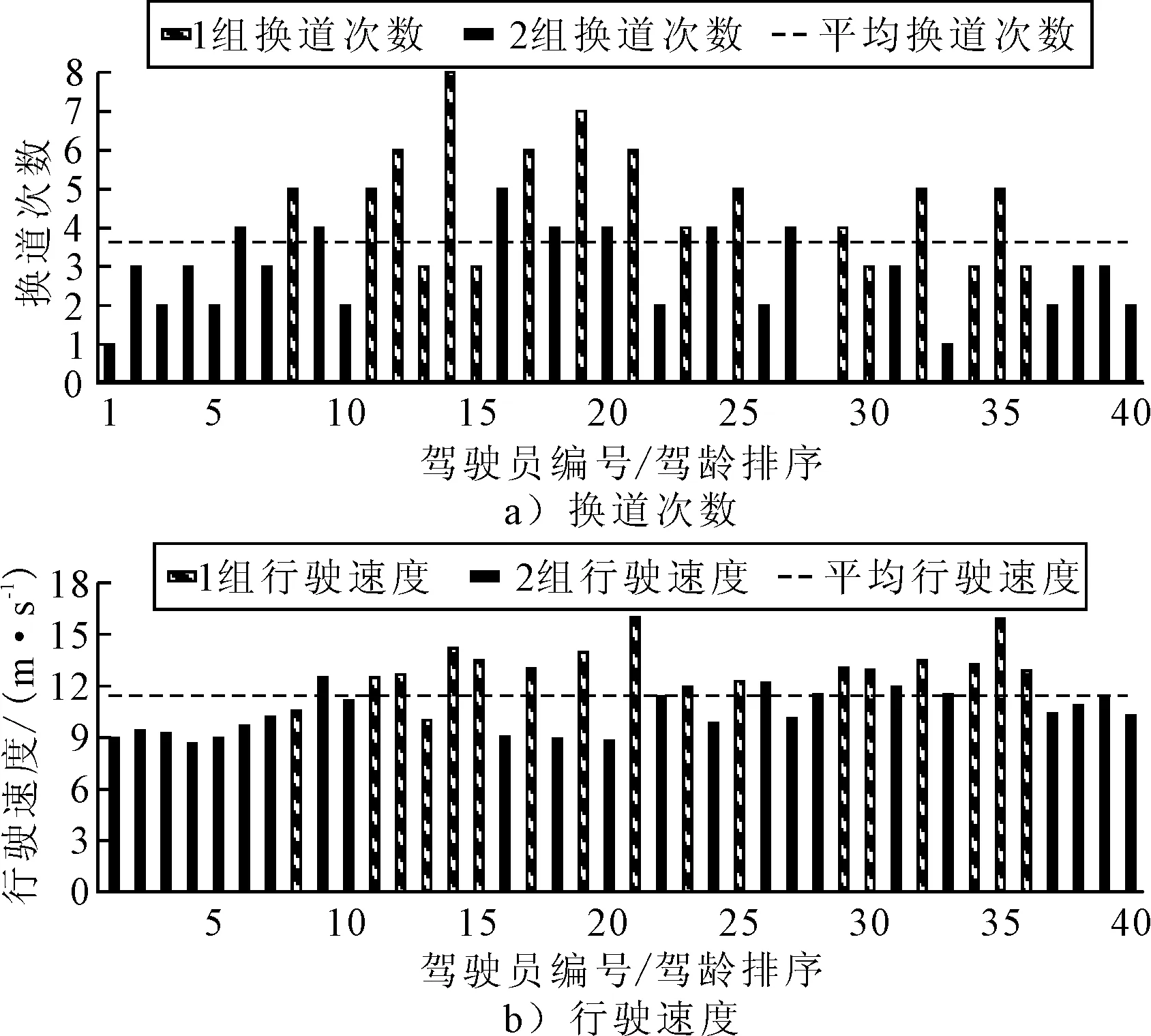
图7 驾驶员换道次数和行驶速度分布图

对驾驶员的平均换道持续时间进行分析,图8a)为40名驾驶员的平均换道持续时间分布频率图,由图8a)可知:驾驶员平均换道持续时间基本处于2～12 s,其中42.5%的驾驶员平均换道持续时间为4～6 s,32.5%的驾驶员平均换道持续时间为6～8 s,该结论与参考文献[6]的研究结论近似相符.图8b)为1组和2组的驾驶员平均换道持续时间分布图,由图8b)可知:2组稳重类型的驾驶员平均换道持续时间主要为4～6 s和6～8 s,占2组总数的82.6%.1组活跃类型的驾驶员平均换道持续时间分布较为分散,没有特定规律,2～4 s快速换道的驾驶员主要为1组成员.

图8 平均换道持续时间频率和分布图

对驾驶员的平均换道横向偏移距离进行分析,图9为40名驾驶员的平均换道横向偏移距离分布图.

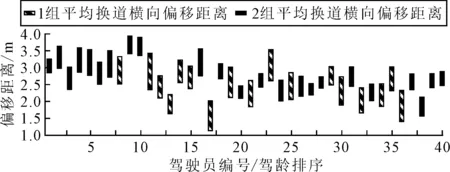
图9 平均换道横向偏移距离分布图

由图9可知:1组活跃型驾驶员平均换道横向偏移距离区间跨度普遍较长,说明该类驾驶员横向偏移距离没有特定分布趋势,换道时间与换道横向位移表现出随机性.2组稳重型驾驶员平均换道横向偏移距离区间跨度普遍较短,表现出明显的个人驾驶行为习惯,换道位移趋于区间中间值,其中低驾龄的成员平均换道横向偏移距离普遍比高驾龄的成员大.

3 结 论

1) 基于北斗高精度定位技术获得车辆出行的若干个轨迹点数据,构建了换道行为识别模型,最终输出直线路段上车辆换道次数、行驶速度、换道持续时间、换道横向偏移距离四类数据.

2) 利用spss软件对输出数据进行层次聚类分析,将驾驶员换道次数、行驶速度作为变量,将驾驶员编号作为聚类样本,按照变量对不同编号的驾驶员进行Q型聚类,聚类算法将驾驶员分为稳重型和活跃型两组类别.

3) 分类别对模型输出数据进行分析,发现活跃型驾驶员换道次数较频繁,行驶速度较快,换道时间和横向偏移距离较为随机,快速换道多为活跃型驾驶员,该类型驾驶员多处于中间层驾龄.稳重型驾驶员主动换道行为较少,行驶速度相对不高,换道时间与横向偏移距离表现出明显的驾驶习惯特征,这类驾驶员平均换道持续时间主要分布在4～6 s和>6～8 s,多为低驾龄、行车谨慎和高驾龄、操作平稳的人群.

4) 模型建立前期仅依据相关参考文献和现有换道轨迹样本数据对换道各阶段的行为特征进行总结、归纳和分析.由于样本量有限,所得到的换道持续时间范围、角速度相同轨迹点数量等阈值仅基于参考文献和有限样本的结论,其普适性可能无法保障.未来研究需进一步扩大样本数量,并通过变换道路等级、试验车类型、终端定位精度等多重变量,开展换道行为阈值的有关研究.