考虑车辆跟车及换道交互参数的驾驶风格识别
柳祖鹏 罗陈怡 严运兵
(武汉科技大学汽车与交通工程学院 武汉 430065)
0 引 言
驾驶风格指一个人选择开车的方式或习惯性的驾驶方式[1],包括驾驶员注意力、自信的习惯性水平,对驾驶速度、行车间距的选择等[2],受到同驾驶有关的态度和信念的影响[3],也受到驾驶员的一般需要水平和价值观的影响[4].
Li等[5]提出采用驾驶模式转移概率评测驾驶风格的方法,比采用传统的驾驶模式频率方法识别准确率更高.Munoz等[6]指出如果在驾驶模式转移概率的基础上加入对驾驶人眼动行为的分析,驾驶风格评测效果会更好.邓涛[7]提出通过节气门开度、节气门开度变化率,以及制动减速度对驾驶风格进行识别.吴振昕等[8]认为驾驶员的驾驶风格主要反应在车速、纵向加速度、油门踏板开合度、侧向加速度、横向角速度、航向角、转向盘转角及其角速度等八个方面.Langari等[9]通过平均加速度和加速度标准差与平均加速度的比值进行驾驶风格识别.Iván等[10]选用车辆在行程过程中的平均加速度、平均减速度,以及突然加速与制动事件发生的总次数作为特征参数用以区分驾驶员的驾驶风格.
上述研究大多基于车辆自身的运动参数特征来识别驾驶员的驾驶风格,较少考虑不同车辆驾驶员之间的交互因素对于驾驶员风格的影响.而驾驶员的跟驰与换道行为又受到道路中其他车辆的制约,驾驶员在其他车辆影响下采取的行动也是驾驶风格的一个重要反映.故本文进行驾驶风格识别时,考虑驾驶员自身运动参数同时,加入驾驶员的跟车时距和换道允许间距,作为车辆跟驰和换道行为中受道路中实行车辆影响的交互参数,提高驾驶风格识别指标的全面性.
1 数据集
文中使用美国开源数据下一代仿真(the next generation simulation, NGSIM)数据集,该数据集记录了车辆运行过程中车辆编号、车辆类型、位置信息、车辆速度、车辆加速度、车头时距、车头间距,以及前后车编号.
文中用NGSIM子集US101路段数据集进行研究.US101数据集是从美国101号高速公路上采集到得到的,测量区域长度为640 m,包含5条主线车道和一条集散车道,见图1,集散车道位于Ventura Boulevard入口和Cahuenga Boulevard出口之间.共8台同步摄像机安装在紧邻高速公路的一个36层楼高的顶部,记录车辆进出入测量区域的情况.并以0.1 s的时间间隔采集通过测量区域的车辆的时空信息,数据具有较高的精确性.

图1 US101数据采集区域示意图
检测路段内小汽车占比较多,约为总数据量的97.3%,文中将小汽车选为研究对象,只考虑小汽车的运动状态参数.
将下载的csv格式数据导入,对数据进行初步处理,剔除摩托车和大型车数据,写入车辆横向速度与加速度,将英制单位转换为国际单位并提取车辆换道时长及其换道时的车间间隙.完成数据的筛选之后,对满足要求的车辆数据进行重新编号,按照相应编号对车辆数据进行存储.
2 驾驶风格参数选择及模糊评价
2.1 参数选择
驾驶员的驾驶风格同驾驶员操纵车辆的行为表现之间存在一定联系[11].相应的,驾驶员操纵车辆的行为表现也能反应出驾驶员的驾驶风格[12].基于各驾驶参数对驾驶员的影响,结合文献[13-14],选择平均车速、速度标准差、横向加速度最大值、横向加速度标准差、跟车时距比例作为评估驾驶员激进程度的指标.同时考虑车辆换道参数对驾驶风格的影响,增加换道时间及换道时目标车道的允许间隙两个指标来评估驾驶员的激进程度.
2.2 模糊矩阵构建
在模糊集合涉及的论域U上,给定一个映射.
(1)
式中:qij为第i个评价对象关于第j个评价指标的隶属度.
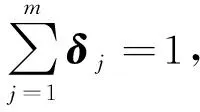
(2)
对数据进行模糊处理时,首先确定其隶属度函数.模糊分布的论域为实数域,一般常用的隶属度函数为梯形和半梯形的形式,见图2.
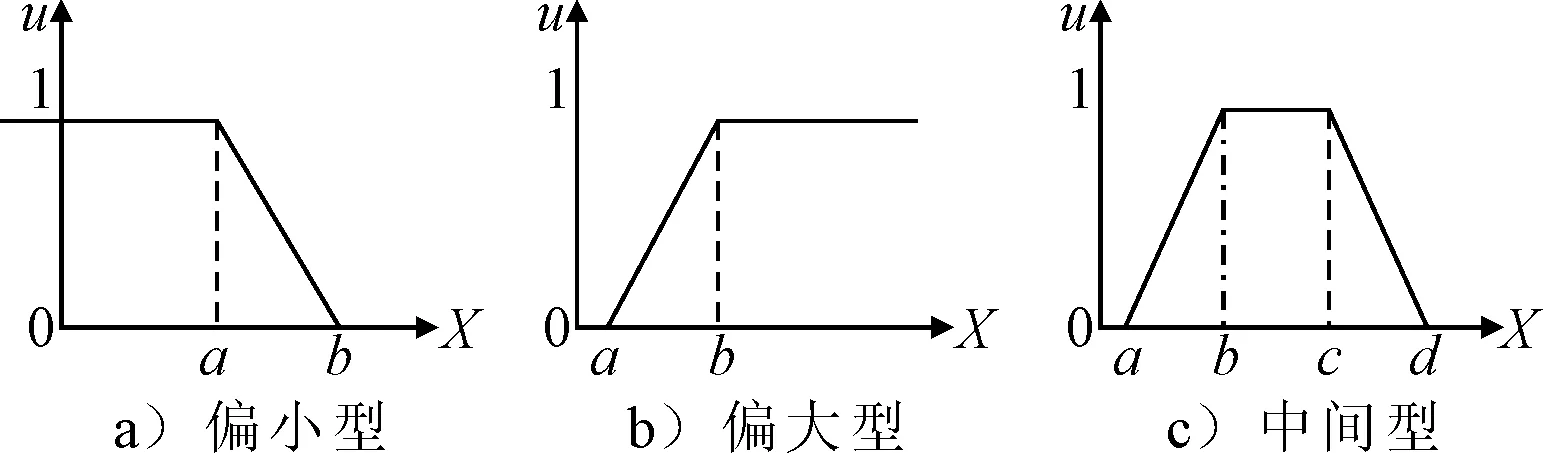
图2 梯形分布
2.3 隶属度函数确定
车辆在区域的行驶速度受交通环境影响,参考车辆限速设置,基于车辆速度分布特点,采用半梯形分布方法确定车辆平均速度的隶属函数,参考车道限速设置,取局部区域速度值的15%和85%分位数作为隶属度函数的分段阈值.车辆平均速度越大,表明该驾驶员相对于其他驾驶员更为激进,故选取偏大型隶属函数,其中,a=4.56 m/s,b=13.71 m/s.
车辆在一段行程中,其纵向速度标准差越大,表明驾驶员在行驶过程中驾驶状态越不稳定,相比较而言其行为波动更大,激进程度也会更大,故选取偏大型的梯形分布作为其隶属函数,其中,a=2.06 m/s,b=4.54 m/s.
横向加速度最大值是驾驶员横向操作的重要参数,驾驶员越激进,其对于车辆的横向行为操纵幅度越大,故选取偏大型的梯形分布作为其隶属函数.其中,a=2.33 m/s2,b=3.95 m/s2.
横向加速度标准差表征驾驶员在车辆横向操纵上的稳定性,驾驶员驾驶风格越保守,其横向操纵行为就会越趋向于平稳,横向加速度标准差也会越小,基于此,选取偏大型的梯形分布作为其隶属函数.其中,a=0.38 m/s2,b=0.56 m/s2.
车头时距表征的是驾驶员在跟车过程中对于安全距离及前向碰撞风险的把握,驾驶员跟驰过程中车头时距越小,表明其驾驶行为越危险,驾驶风格也更加激进.计算驾驶员在整个测量区间中,跟车时距小于1.5 s的时长占整个测量时长的比例,以此比例作为驾驶员在车头时距的评判标准下对于激进程度的隶属度.表1为跟车时距比例.

表1 跟车时距比例
换道时间是车辆换道行为的重要体现,表明了车辆在换道过程持续情况,换道时间越短,表明驾驶员行为越激进,故选用偏小型梯形分布表示换道时间的隶属函数.其中,a=1.9 s,b=6.1 s.
目标车道换道间隙为在本车换道开始前一时刻,目标车道前后车之间的空间距离,换道间隙越小,本车同目标车道前后车碰撞可能性越大,相对应的驾驶员也更加激进,故选取偏小型梯形分布作为换道间隙的隶属函数.其中,a=25.98 m,b=58.61 m.
2.4 特征权重确定

(3)
根据自适应权重算法得知,当满足方差最小时所对应的最优加权因子为
(4)
方差近似估计算法为
(5)
式中:Rii为Xi的自协方差函数;Rij为Xi和Xj的互协方差函数,其值可由其时间阈估计值得到.
(6)
(7)
式中:k为测量次数.
基于自适应权值估计算法得到的各特征参数的权重见表2.
2.5 驾驶风格分类
根据式(1),计算出每个驾驶员的综合评价指数,见表3.

表3 驾驶员评价指数表
2.6 与k-means聚类方法的比较
由特征值权重的确定可以知道,本文所选参数相关性较低,近似可看作相互独立,故不用对其进行降维处理.基于数据边界,对数据进行归一化,将数据映射到0~1,消除单位对于数据分布的影响.
k-means算法是一种基于数据点空间特性进行分类的无监督分类方法,以欧氏距离作为衡量样本空间上聚集性的指标,将空间上聚集性相近的点划分为一个类别,然后计算每个类中样本的平均值作为新的聚类中心,进行下一次迭代,直到聚类中心不再变化或者达到迭代次数达到上限,确定最终的分类结果.
k-means聚类完成后,其三簇的聚类中心见表4.

表4 k-means聚类中心
3 分类结果分析
依据车辆驾驶员驾驶激进值的分布情况,以0.4和0.6为阈值划分不同激进程度驾驶员所属的驾驶类别.保守型、普通型、激进型的驾驶员实例数分别为37、83、69.k-means算法分类得到保守型、普通型、激进型的驾驶员的实例数分别为57、75、57.两种分类方法分类结果的一致性为40.21%.
驾驶员特性雷达图见图3~6.由图3~6可知:同时存在换道与跟驰行为的车辆中,车辆的换道时间大多较为迅速.
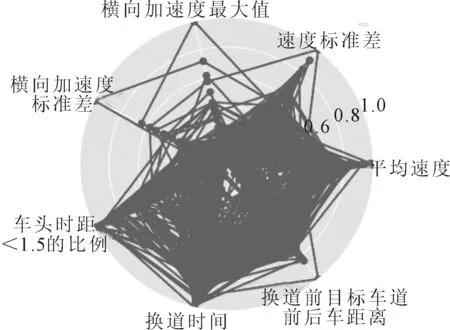
图3 所有驾驶员特性雷达图

图4 保守型驾驶员驾驶特征雷达图

图5 普通型驾驶员驾驶特征雷达图
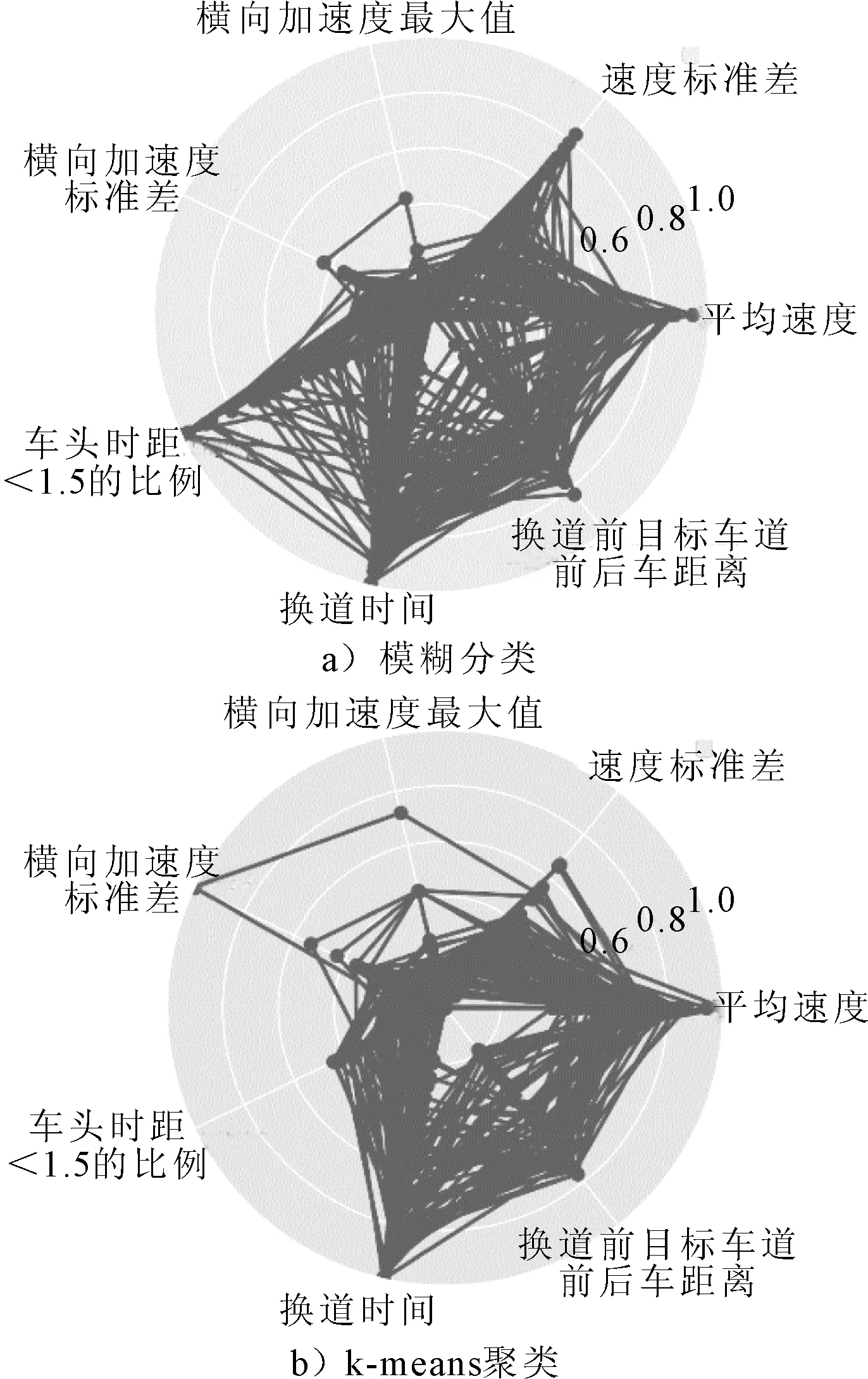
图6 激进型驾驶员驾驶特征雷达图
分别采用k-means聚类和模糊数学的方法对驾驶员驾驶风格进行分析,对于前者的分类结果而言,保守型驾驶员的纵向速度标准差和换道时的允许换道间距在分类中存在明显的聚集,其允许换道距离较小且纵向速度标准差较大,车辆在行驶过程中速度变化相较而言更为剧烈;普通型的驾驶员则在纵向平均速度上表现出聚集,由较大的平均速度;激进型驾驶员则在车头时距和纵向速度上表现出聚集,跟车时距小于1.5 s所占的行程时间较多,在跟车行为上存在更大的危险性.采用模糊数学方法对车辆驾驶员进行驾驶风格划分,划分为保守型的驾驶员驾驶特征的聚集性更多的表现在雷达图的右下侧,普通型的驾驶员比较起来,分布与保守型的驾驶员相类似,但各方面的值都要大于保守型的驾驶员,激进型的驾驶员特征参数同其他类型的驾驶员类似,但相应数值会更大,在整个雷达图中所占面积也最大.
将标准化的数据还原到原始数据中,见表5,采用模糊分类的方法对驾驶员的驾驶风格进行识别时,随着驾驶员激进程度的增加,驾驶员各项指标值都呈现递增状况,而k-means聚类则无该规律,直观上而言,模糊分类结果比k-means聚类结果更能体现驾驶员的激进程度,更适合于车辆跟车及换道等行为的安全性评估.

表5 不同类型驾驶员类间均值
4 结 束 语
本文目前所用的数据集只收集了各个驾驶员较短的一段时间内的驾驶参数特征,对于描述驾驶员的驾驶风格而言数据时长较短,只能表征驾驶员在观测路段的风格,对于驾驶员常态风格的识别与分类能力还是较弱,后续研究将考虑扩大使用的数据量,标定驾驶员的激进程度,用于评估驾驶员在操纵车辆中的碰撞风险.

