基于动态排队论的大型邮轮舾装物料拣货资源配置鲁棒优化模型研究
周 杨 杨家其 丛 喆
(武汉理工大学交通与物流工程学院 武汉 430063)
0 引 言
邮轮建造具有单船定制性强、物流集配层级复杂、多专业多地域协同、生产全过程控制难及工作量大的特点,在现代造船模式下,其物流作业具有多批次、小批量、多品种的特点.舾装物料的配送是邮轮建造的基础,并影响邮轮建造的进度和成本[1].拣货作业作为配送的关键环节,其作业效率过慢,导致物料供给不及时;其作业效率过高,要求作业资源较多,导致拣货作业成本过高,因此对其作业资源的配置显得十分重要.
在建造物资集配方面,邮轮具备较一般船舶物资出入库更频繁、种类更繁多且数量更庞大的特点,其过程更为繁杂[2-3].邓硕等[4-6]针对现代造船模式提出了托盘化管理,分析了如何强化舾装物料的管理,并通过实例,利用程序分析法、MECE方法、层次分析法探讨了分段生产中的资源配置问题[4-6].
我国造船物流领域仍以劳动力结合机械设备作业为主,因此需要针对作业资源进行优化配置.排队论广泛应用于生产作业流程分析和资源配置决策领域,静态排队论在仓储作业资源、港航作业资源配置等领域均有应用[7-10].而静态排队论与实际生产作业情况相差较大,所以一些学者开始研究服务率和输入率不断变化的动态排队论方法[11-12].动态排队论模型能够根据实际状况调整服务效率和输入率,亟需将这一优势应用于舾装物料拣货作业这类复杂的作业流程分析上.另外以往有关作业资源配置的研究主要对人力、作业器械进行单方面的配置[13-15],没有考虑到边际报酬递减规律、设备类型及人力与设备配比对作业效率带来的影响.
邮轮建造工期较长,造船市场环境多变,不同情况下作业效率要求、人力成本等要素往往出现变化.因此需针对出现的扰动对决策模型进行鲁棒性优化,使得最优解对于突发情况具有一定的稳定性[16-17].文中在考虑边际报酬递减、设备配比、设备类型的同时,将动态排队模型与鲁棒优化模型进行结合,搭建基于单位时间总成本最小的拣货资源配置模型,对拣货作业的小组数量、设备类型、设备配比等进行鲁棒配置决策,为船舶制造厂舾装物料的拣货资源配置提供支持.
1 问题描述及假设
拣货作业是依据顾客的订货要求或配送中心的送货计划,尽可能迅速、准确地将商品从其储位或其他区域拣取出来,并在将其集中在配货区域等待配货的作业流程.
邮轮舾装物料的集配中心与电商物流配送中心一样具备小批量、多批量次的特点,但货物品类更繁杂,包括各类价值、体积、重量差异较大的物料,加之舾装物料主要以舾装托盘为作业单元,处理起来较为繁琐,所以其作业设备也主要为叉车、行车等,同时还需控制作业订单总量,防止因订单过多导致作业紊乱,影响物流进程.在舾装物料集配中心往往存在设备不能满足工人作业需求的问题,即存在配比不合理,另外不同型号设备的作业成本、作业效率和碳排放量等均不相同,不同配比导致的作业成本和效率也不同,因此需要考虑作业设备的选型和配比问题.
在邮轮舾装物料的拣货作业当中,将集配系统分配的订单视为顾客源,作业小组及相应设备视为排队系统中的服务台.同时提出如下假设.
1) 拣货部门按照先到先处理的规则进行处理,在处理先到的订单时,其他订单只能处于等待状态,且不存在紧急订单.
2) 拣货作业成本主要包括人力成本和机械固定成本、碳排放成本、与处理订单量相关的变动本,每个小组分配相同数量的机器.
3) 各个作业小组的订单处理时间相互独立.
2 模型构建
2.1 物料拣货的动态排队论分析
1) 舾装物料订单的动态输入率 当至少有一个拣货组空闲时,输入率保持不变;而所有拣货组都繁忙时,为保证舾装物料的拣货质量,输入率与系统中的物料订单数量呈负相关;当订单数量达到最大订单容量时,其输入效率应该暂时为0,一旦降低后就会立刻继续输入,为
(1)
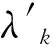
2) 服务台的动态服务率 当舾装物料拣货系统中堆积的订单变多时,拣货组会逐渐提高作业速度,当拣货系统中的订单数量达到最大时,小组作业速度也会到达最大值,为
(2)
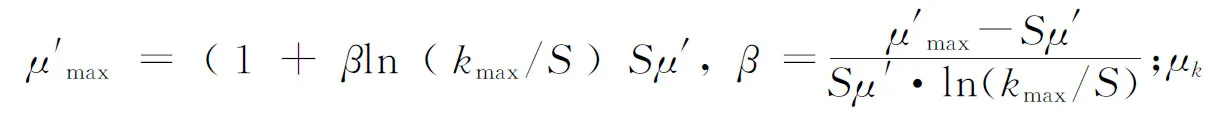
3) 动态排队论的相关指标 不同的资源配置将会得到不同拣货作业排队系统参数,得到此动态排队系统中的状态概率为
(3)
式中:P为此排队系统空闲的概率.
(4)
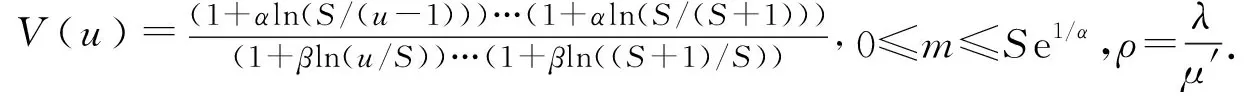
根据式(1)~式(4)算得排队系统平均输入效率为
(5)
排队系统平均队长为
(6)
排队系统平均处理效率为
(7)
由Little公式,根据式(5)~式(6)计算单个订单平均逗留时间为
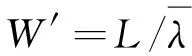
(8)
2.2 确定型模型构建

(9)
(10)
(11)
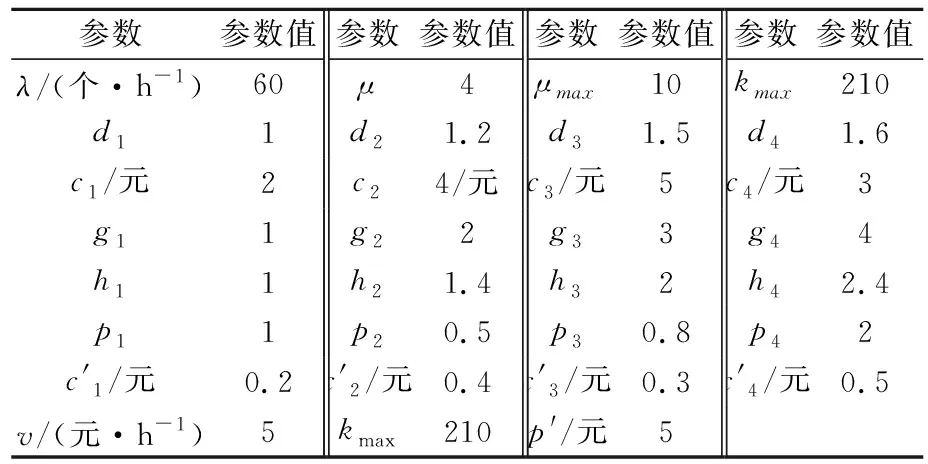
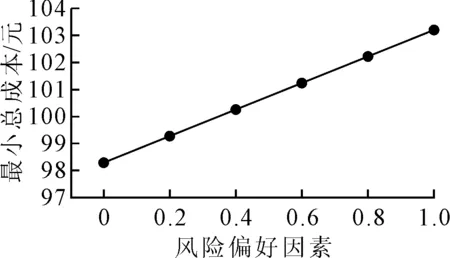
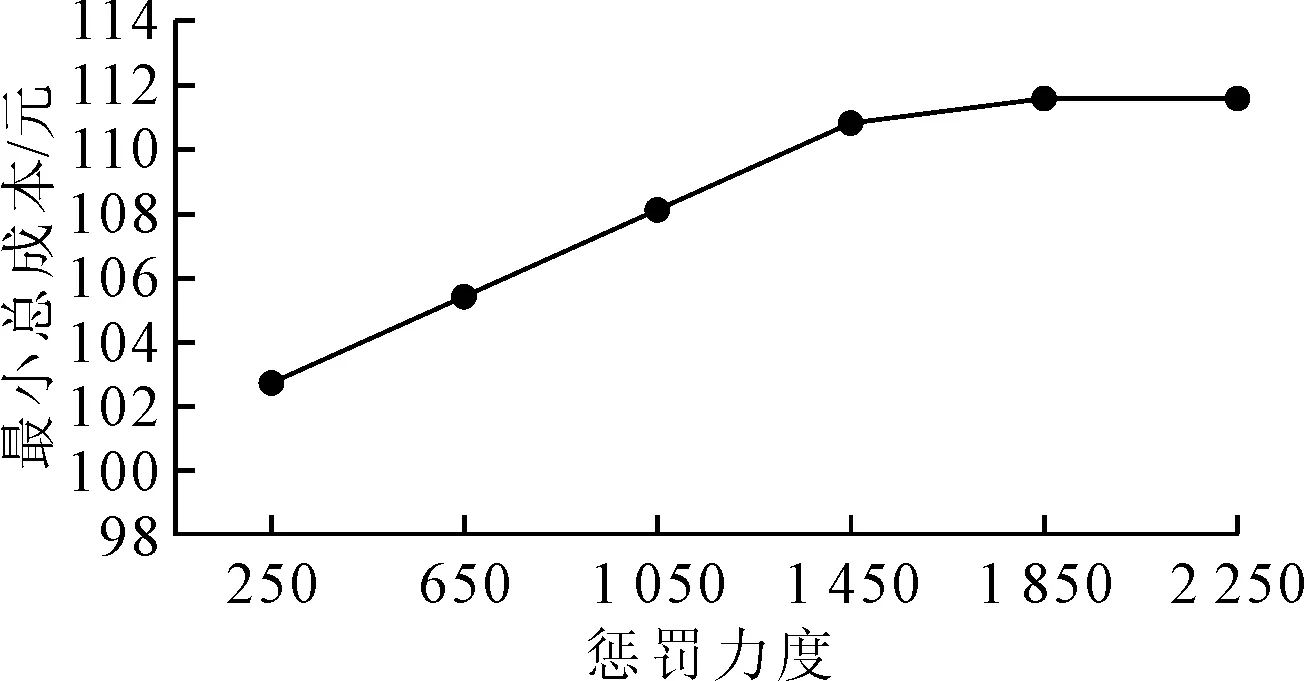
W′ (12) S∈D且为整数 (13) (14) (15) (16) (17) gj≥1且为整数 (18) di>0hj>0μ>0μmax>0kmax>0 (19) 邮轮建造不同时期面临的生产环境不同,人力成本的波动、舾装物料供应商供给能力变化以及船舶交货期延期等因素影响,对于拣货效率要求也会变化,作业时间要求也会相应调整.当有关参数发生变化时,需要对作业资源进行调整. minσ(u,y1,y2,…,ys)+wγ(ε1,ε2,…,εs) 约束为 Asu+Bsys+εs≤bs Ey≤e x,ys≥0 式中:E为确定参数;u为结构型变量;As、Bs为不确定参数.目标函数中第一项σ(·)为解的鲁棒性,第二项为控制性约束被违反的惩罚成本;w为加权系数,表示模型的鲁棒性及解的鲁棒性之间的权衡. (20) (21) (22) (23) (24) 基于某造船厂物流中心舾装件拣货的调研数据,设置拣货作业系统参数见表1. 表1 拣货作业系统参数 另外假设该船厂舾装物料配送中心存在6种可能的情景(可根据实际情况调整情景数量),见表2. 表2 不同情景的概率、人力成本及作业时间要求 利用Gurobi求解器进行求解,模型中的参数τ取值为0.9,ω为250,求解得到单个订单处理的总成本最小为102.71元,此时S=2,x1=0,x2=0,x3=1,x4=0,y1=0,y2=0,y3=1,y4=0,订单的平均逗留时间为0.102 h,能够满足多数情景下的作业效率要求,即安排了2个小组,且每个小组配备3套第3种设备. 利用确定型模型对每个情景进行求解,求出每个情景的最优值和配置方案,见表3. 表3 不同情景下的配置方案及最小成本 由表3可知:鲁棒模型的结果在满足多数情景作业效率要求的同时,与五种情景的最小成本相差在10%以内,其得到的配置方案与各确定情景的方案都较为接近.由于情景6作业效率要求严格且人力成本高,导致其总成本过高,但这类情况出现较少.这说明在一定的风险偏好和惩罚力度下,鲁棒优化模型做出的资源配置方案及其产生的最小成本和作业效率,都较为接近多数情景的最优解且满足多数情景的作业效率要求. 1)τ的敏感性分析 当τ越大决策者越希望规避风险.当ω保持250不变时,现分别对参数τ取0、0.2、0.4、0.6、0.8、1,绘制图1.随着τ的增加,单位时间的最小成本也随之增大.因为当τ越大,说明决策者越保守,因此为规避风险而得到做出的决策会导致成本更高. 图1 τ敏感性分析 2)ω的敏感性分析ω为时间约束被违反时的惩罚力度,是用来衡量鲁棒性的一个重要权重,其值越大代表违反约束的成本越高.当τ保持0.9不变时,现对ω分别取250、650、1 050、1 450、1 850、2 250,绘制图2.当ω越大,那么其惩罚成本越大,如果想避免惩罚成本,那么需要提升作业资源配置,也可能会导致成本增加,见表4.由表4可知:反映了未满足作业时间约束时的惩罚成本,当ω足够大时,由于惩罚力度过大,那么提升资源配置更合理,惩罚成本为0,说明鲁棒性随着的ω增大而变强. 图2 ω的敏感性分析 表4 惩罚成本随ω变化的情况 文中利用动态排队论对邮轮舾装物料拣货作业进行拟合,在考虑边际报酬递减、设备型号、设备配比等因素的基础上,搭建了以最小总成本为目标的拣货资源配置确定型模型.考虑建造环境的不稳定性,结合鲁棒优化理论,搭建了拣货资源配置鲁棒优化模型.根据调查数据设置算例,假设存在6种不同情景,设定风险偏好和约束违反惩罚力度,利用Gurobi求解,得到最小总成本及对应的作业资源配置方案,并与6种确定型情景下的最小成本进行对比,除情景6较为极端外,成本相对差均在10%以内.对τ、ω进行敏感性分析,以及对成本及鲁棒性的影响.本研究在模型中对于作业收益以及人力资源边际报酬递减规律进行了简化处理,后续研究将搭建更符合实际的邮轮舾装物料拣货资源配置决策模型.

2.3 资源配置的鲁棒性
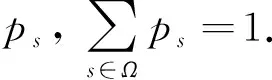
2.4 鲁棒优化模型

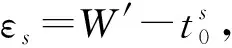
3 算例分析
3.1 算例设置
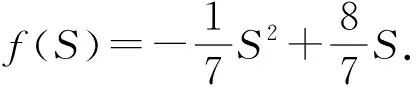

3.2 算例求解

3.3 敏感性分析

4 结 束 语

