内置式开关阀液压减振器阻尼力模型构建

杨华 李尚荣 殷吕 游致远

（1.上海保隆汽车科技（安徽）有限公司，合肥 230061；2.合肥学院，合肥 230601）

1 前言

汽车减振器是影响车辆行驶平顺性、操控性、舒适性与安全性的重要部件，主要经历了干摩擦式减振器、鼓式减振器、臂式减振器、双筒液压减振器和单筒预充气式减振器等阶段[1-3]。受结构和成本的影响，双筒电流变减振器和磁流变减振器还处于研发和推广阶段[4]。传统液压减振器主要依靠工程师的经验实现其性能调优，驾乘的平顺性与安全性难以兼顾。为解决该问题，阻尼可调减振器应运而生，电磁阀式阻尼可调减振器是典型的阻尼可调减振器[5-11]。根据调节原理，阻尼可调减振器可分为节流口面积可调式和减振油液粘度可调式，其中节流口面积可调式减振器最为常用。本文以一种节流口面积可调式减振器——内置式开关阀液压减振器为研究对象，分析其结构与工作原理，建立其阻尼力模型，并通过仿真和试验验证其准确性。

2 内置式开关阀液压减振器的基本结构与工作原理

内置式开关阀减振器与传统双筒液压减振器结构相似，二者的主要区别为内置式开关阀减振器复原阀内部设有电磁线圈控制的阀门。开关阀芯的电磁线圈断电时，开关阀芯由预紧弹簧固定在位移极限处，开关阀芯流通孔被遮挡，此时减振器相当于传统双筒液压减振器，将复原阀与压缩阀预设成高阻尼状态，可以提高行驶安全性，如图1a所示。当电磁线圈通过一定大小的电流时，线圈产生电磁吸引力，压缩预紧弹簧，开关阀芯接触电磁线圈铁芯，此时开关阀芯流通孔联通油液，相当于减振器增加了流通旁路，阻尼力降低，提高了车辆行驶的平顺性，如图1b所示。

图1 内置式开关阀减振器结构与工作原理

3 减振器阻尼力模型

基于缝隙流动、管嘴流动、薄壁小孔流动、细长孔流动，运用串联流体和并联流体的计算理论，将复原阀系内部、压缩阀系内部、开关阀内部的油液流动视为串联的液压管路油液流动，将经过复原阀系、压缩阀系及开关阀的油液流动视为并联的管路油液流动。管路特点为[12]：

a.油液在串联管路中的压差等于各分段流动产生的压差总和。

b.油液在串联管路中流经各分段的流量相等。

c.油液在并联管路各分支段产生的压差相等。

d. 油液在并联管路中的总流量等于各分支段流量的总和。

根据上述设定条件，分别在电磁线圈断电和通电条件下分析内置式开关阀液压减振器复原行程与压缩行程的阻尼特性。

3.1 电磁线圈断电时

当电磁线圈断电时，开关阀芯受预紧弹簧作用，限定在位移极限处，此时开关阀芯流通孔被遮挡，内置式开关阀液压减振器相当于传统双筒液压减振器。复原行程中，当活塞速度未达到开阀速度时，复原腔的油液通过活塞上的复原节流阀片、复原常通节流孔流入压缩腔，当活塞速度达到复原阀开阀速度时，复原阀打开，油液增加了经过复原阀座节流孔在复原阀片处形成的环状缝隙路径，即复原行程根据活塞速度分为复原阀关闭与打开2个阶段。压缩行程中，活塞相对工作缸向下运动，压缩腔的一部分油液通过活塞上的复原常通节流孔、复原节流阀片流入复原腔，一部分油液通过压缩阀座节流孔、压缩节流阀片、压缩阀进入储油腔。压缩阻尼较复原阻尼小，所以压缩行程只对压缩阀开阀后进行分析。

3.1.1 复原阀关闭时

设经过活塞阀系处的总流量为Q1、压差为p1，经过复原节流阀片的流量为Q11、压差为p11，经过复原常通节流孔的流量为Q12、压差为p12，如图2 所示。根据串联流动理论[2]，有：

图2 复原阀关闭时油液流动示意

其中，经过复原节流阀片的流量Q11为薄壁小孔流量，经过复原常通节流孔的流量Q12为细长孔流量：

式中，c1为薄壁小孔流量系数；A1为复原节流阀片开口总面积；ρ为油液密度；n1为复原常通节流孔数量；d1为复原常通节流孔直径；μt为绝对粘度；l1为复原常通节流孔长度；v为活塞运动速度。

设减振器充气压力为pg，复原行程开阀前的阻尼力为Freb1，由式（1）～式（5）可得：

式中，AV为活塞有效面积；AP为活塞杆横截面积。

3.1.2 复原阀打开时

设复原阀开阀后增加的流量为Qlop、压差为plop，经过复原阀座节流孔的流量为Q13、压差为p13，经过复原阀片处的环状缝隙流动流量为Q14、压差为p14，如图3所示。根据串联流动理论[12-13]可得：

图3 复原阀打开后油液流动示意

其中，Q13为细长孔流量，Q14为环状缝隙流量：

式中，n2为复原阀座节流孔数量；d2为复原阀座节流孔直径；l2为复原阀座节流孔长度；δf为阀片开度；r1bf为复原阀片外半径；r1kf为复原阀片阀口位置半径。

设复原行程开阀后总流量为Qreb2、总压差为p′reb，记此状态经过复原节流片、复原常通节流孔处的总流量为Q′1、压差为p′1，根据并联流动理论[14]可得：

设复原行程开阀后的阻尼力为Freb2，由式（7）～式（13）可得：

3.1.3 压缩阀开启后

设经过活塞上的复原常通节流孔、复原节流阀片进入复原腔的总流量为Q2、压差为p2，经过复原常通节流孔的流量为Q21、压差为p21，经过复原节流阀片的流量为Q22、压差为p22，如图4 所示。根据串联流动理论[12-13]可得：

图4 压缩行程中活塞处的流动示意

其中，Q21为细长孔流量，Q22为薄壁小孔流量：

设经过压缩阀系处的总流量为Q3、压差为p3，经过压缩阀座节流孔的流量为Q31、压差为p31，经过压缩节流阀片的流量为Q32、压差为p32，经过压缩阀的流量为Q33、压差为p33，如图5 所示。根据串联流动理论[13-14]可得：

图5 压缩阀油液流动示意

其中，Q31为短孔流量，Q32为薄壁小孔流量，Q33为环状缝隙流量：

压缩阀系处的压差p3为：

式中，c2为短孔流量系数；A2为压缩阀座节流孔总流通面积；A3为压缩节流阀片开口总面积；r2bf为压缩阀片外半径；r2kf为压缩阀片阀口位置半径。

设压缩行程阻尼力为Fcom，由式（15）～式（24）可得：

3.2 电磁线圈通电时

当电磁线圈通过一定大小电流时，开关阀芯受到电磁线圈的吸引力，压缩预紧弹簧，最终接触电磁线圈铁芯，开关阀芯流通孔完全露出。油液经过电磁阀外壳流通孔进入流通阀体与电磁线圈形成的腔室中，再经开关阀芯流通孔进入流通阀体与活塞连接杆形成的腔室，最后经活塞连接杆流通孔进入压缩腔，此时减振器相当于增加了流通旁路，阻尼力降低。

3.2.1 复原阀关闭时

电磁线圈通电前、后复原阀系处的流动相似，故设此状态经过复原节流片、复原常通节流孔处的总电流量为Q″1、压差为p″1。设由电磁阀经过的总流量为Q4、压差为p4，经过电磁阀外壳流通孔的流量为Q41、压差为p41，进入流通阀体与电磁线圈形成的腔室流量为Q42、压差为p42，经过开关阀芯流通孔的流量为Q43、压差为p43，进入流通阀体与活塞连接杆形成的腔室流量为Q44、压差为p44，经过活塞连接杆流通孔进入压缩腔流量为Q45、压差为p45，如图6所示。

图6 电磁阀通电、复原阀关闭时油液流动示意

根据串联流动理论[12-13]可得：

其中，Q41、Q43为短孔流量，Q42、Q44为过流端面突然扩大的流量，Q45为细长孔流量：

式中，A4为电磁阀外壳流通孔的总流通面积；ξ为局部阻力系数；A5为开关阀芯流通孔的总流通面积；d3为活塞连接杆流通孔直径；l3为活塞连接杆流通孔长度；v42为油液流过流通阀体与电磁线圈形成的腔室的速度；v44为油液流过流通阀体与活塞连接杆形成的腔室的速度。

设此状态下由复原腔进入压缩腔的总流量为Q5、压差为p5，根据并联流动理论，有：

设电磁线圈通电后、复原阀关闭时复原行程阻尼力为F″reb1，由式（26）～式（35）可得：

3.2.2 复原阀打开时

电磁线圈通电前、后复原阀系处的流动相似，设复原阀开阀后增加的流量为Q'lop、压差为p'lop，记此状态经过复原节流片、复原常通节流孔处的总流量为Q‴1、压差为p‴1，由电磁阀经过的总流量为Q'4、压差为p'4，设此状态下由复原腔进入压缩腔的总流量为Q'5、压差为p'5，如图7所示。

图7 电磁阀通电、复原阀打开时油液流动示意

根据并联流动理论[12-13]可得：

设电磁线圈通电后、复原阀开阀后复原行程阻尼力为F'red2，由式（37）～式（39）可得：

3.2.3 压缩阀打开时

电磁线圈通电前、后流经压缩阀系处的油液流动相似，设经过活塞上的复原常通节流孔、复原节流阀片进入复原腔的总流量为Q'2、压差为p'2，经过压缩阀系处的总流量为Q'3、压差为p'3，经过电磁阀的总流量为Q'4、压差为p'4。

在教育现代化的进程中，信息技术在教学中得到了广泛应用和飞速发展，促进了大学英语课堂教学效果的提升。然而，信息技术在课堂中发挥越来越重要的作用的同时，也对大学英语教学带来了挑战和问题。现代化信息技术介入后，课堂生态中的各类生态因子之间的相互作用受到了影响，加剧了大学英语课堂生态平衡-不平衡-再平衡的循环过程，课堂生态结构和作用上的失衡日益突出。因此，研究信息化语境下大学英语课堂生态的失衡现象，分析其原因，并提出重构大学英语生态课堂的实践策略已经成为必然。

设压缩行程阻尼力为F'com，与式（24）、式（25）类似，可得：

4 减振器阻尼性能仿真

根据内置式开关阀减振器的结构与工作原理和不同工况下阀系的阻尼作用，利用ADAMS/Hydraulics建立该减振器的计算模型，如图8所示。

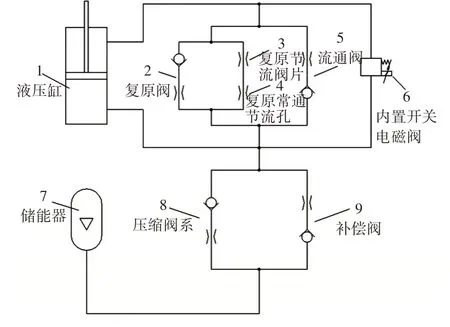
图8 内置式开关阀减振器液压模型

模型中用开启压力较小的单向阀和直径较大的节流孔串联来模拟开启压力较小的流通阀5 与补偿阀7；用开启压力较大的单向阀和直径较小的节流孔串联来模拟开启压力较大的复原阀2 与压缩阀系8；用串联的2 个节流孔模拟复原节流阀片3 和复原常通节流孔4；用电磁控制的可变节流孔模拟内置开关电磁阀6；用液压缸1 模拟活塞、活塞杆与工作缸；用储能器9 模拟储油腔。运用该模型可以将减振器内部结构特征与外特性联系起来，仿真模型主要参数如表1所示[12-14]。

表1 仿真模型各关键参数取值

5 仿真结果与试验数据对比分析

根据QC/T 491—2018《汽车筒式减振器台架试验方法》[15]，减振器试验行程为±30 mm，试验样品温度为20±2 ℃，在MTS 减振器试验台上进行试验，得到速度为0.5 m/s 时不同活塞连接杆流通孔直径条件下内置式开关阀减振器的仿真示功图及试验示功图，如图9所示。

图9 不同活塞连接杆流通孔直径条件下内置式开关阀减振器仿真与试验示功图

由图9可知：

a.电磁线圈断电时，减振器复原与压缩的阻尼力较大；电磁线圈通电时，减振器复原与压缩的阻尼力较小。由式（28）～式（32）可知，改变d3对阻尼力影响最明显：d3=1.2 mm时能使复原阻尼力从700 N变化到2 600 N，压缩阻尼力从600 N变化到1 800 N；d3=1.1 mm 时能使复原阻尼力从1 200 N 变化到2 600 N，压缩阻尼力从900 N变化到1 800 N；d3=1.0 mm时能使复原阻尼力从1 600 N 变化到2 600 N，压缩阻尼力从1 100 N变化到1 800 N。

b.减小d3，当电磁线圈通电时，减振器复原阻尼和压缩阻尼均上升，当电磁线圈断电时，减振器复原阻尼和压缩阻尼几乎无变化。

内置式开关阀减振器阻尼力-活塞位移曲线的仿真与试验结果趋势一致，证明了该模型的正确性。

6 结束语

本文分析了内置式开关阀液压减振器的基本结构及原理，利用串联流体、并联流体等计算理论，建立了内置式开关阀液压减振器的数学模型，利用ADAMS/Hydraulics 对所述减振器进行仿真，并进行了试验验证。结果表明：所建立的仿真模型正确可靠；改变电磁阀内部流动通道的有效面积，特别是活塞连接杆流通孔直径，能增加复原阻尼力和压缩阻尼力，故可通过改变活塞连接杆流通孔直径实现所需的阻尼力变化。