无预紧力变摩擦阻尼器的研发与简谐激励下的动力特性分析

陈家川,赵桂峰,马玉宏,陈舒坪,刘 伟

(1. 广州大学 土木工程学院,广东 广州 510006; 2. 广州大学 工程抗震研究中心,广东 广州 510006; 3. 广东省地震工程与应用技术重点实验室, 广东 广州 510006; 4. 工程抗震减震与结构安全教育部重点实验室,广东 广州 510006)

0 引言

消能减震技术[1-2]是一种行之有效的减震手段,其种类繁多并在我国得到了普遍的运用。消能减震装置一般被称为阻尼器或消能器,能够有效地减小结构地震响应,发挥保障结构安全的作用。摩擦阻尼器是通过2个界面之间的滑动和摩擦耗散能量,具有对荷载及加载频率不敏感、耗能能力稳定、环境适应能力强、构造简单和容易拆卸等优点,因此具有优异的工程应用价值。PALL等[3]在20世纪80～90年代首先提出了Pall摩擦阻尼器,采用X形支撑的方式布置在框架柱之间[4]。在此基础上,各国学者开发了一系列的摩擦阻尼器来满足工程上的各种需求,常见的有平动型摩擦阻尼器[5-11]和转动型摩擦阻尼器[12-17]。现有的摩擦阻尼器无摩擦力放大功能,多数通过预紧力螺栓来施加预紧力[18-19],存在一定的起滑力,若摩擦阻尼器的起滑力较大,阻尼器无法发挥耗能作用,反而导致增加了结构的刚度;起滑力较小则无法充分发挥耗能效果,难以得到理想的减震效果。此外,长期处于预紧力下的摩擦材料间容易出现冷粘结、冷凝固和预紧力易松弛等问题,会导致其力学性能无法准确预测[20]。

针对现有摩擦阻尼器存在的不足,文中基于滚珠丝杠的放大机理和摩擦阻尼器的优点,提出了一种无预紧力变摩擦阻尼器(non-preload variable friction damper,NVFD),该阻尼器具有无需施加预紧力即可提供变化的摩擦力的特点,且具有摩擦力、位移和惯性质量放大效应。文中介绍了该装置的构造及作用机理;通过推导NVFD的恢复力计算公式,给出了其恢复力模型,并开展拟静力试验,验证了恢复力公式和作用机理的正确性,推导了简谐荷载作用下NVFD单自由度减震体系的位移解析解,将4阶Runge-Kutta法计算的数值解结果与解析解进行对比分析,验证了解析解的正确性,同时分析了弹簧刚度和圆环形钢板质量这2个参数对2种解吻合程度的影响;最后根据位移解析解表达式,推导了动力放大系数计算公式,并进行相关参数分析,可用于指导此类阻尼器的设计。

1 NVFD作用机理和恢复力模型

1.1 NVFD作用机理

无预紧力变摩擦阻尼器由滚珠丝杠、圆环形钢板、摩擦片、弹簧、滚珠螺母等构件组成。整体示意图如图1(a)所示。方形钢板1和2上有套筒,用以安装弹簧,方形钢板1通过螺母固定在丝杠的螺纹段,随丝杠一起水平运动,方形钢板2和方形钢板3通过圆环形钢管相连,侧板固定在外框上,摩擦片放置在外框底板上。现以滚珠丝杠向右运动为例(如图1(b)中外力向右所示),介绍NVFD作用机理。丝杠向右水平运动,带动圆环形钢板转动,同时左边方形钢板1推动左边弹簧压缩变形,弹簧压力通过方形钢板2传递给方形钢板3,从而摩擦片与圆环形钢板之间产生正压力,使摩擦片与转动的圆环形钢板摩擦耗能。弹簧压缩量随着丝杠位移的增大而变大,促使正压力增大,摩擦力也随之增大;而在丝杠向右水平运动时,右边方形钢板1会远离右边弹簧,右边圆环形钢板和摩擦片无正压力,此时右边摩擦片不产生摩擦力。若丝杠向左运动,则如图1(b)中外力向左所示。

图1 NVFD示意图Fig. 1 Schematic diagram of NVFD

NVFD的极限位移取决于丝杠预留空间距离或弹簧的有效压缩距离(一般均可远大于设计需求),当丝杠前进或者后退一个螺距(导程),圆环形钢板旋转一周,具有位移放大效应。同时,NVFD具有质量放大和摩擦力放大效应,是因为滚珠丝杠水平运动时会带动圆环形钢板旋转,圆环形钢板旋转产生的转动惯性矩和摩擦片与圆环形钢板摩擦产生的摩擦力矩会导致摩擦力和圆环形钢板质量放大,同时将丝杠转动的切向力转化为轴向运动时丝杠轴向力,会进一步放大质量和摩擦力。

1.2 NVFD恢复力模型

NVFD圆环形钢板受力分析如图2所示,滚珠与丝杠的力学分析如图3所示,参数符号表如表1所示。

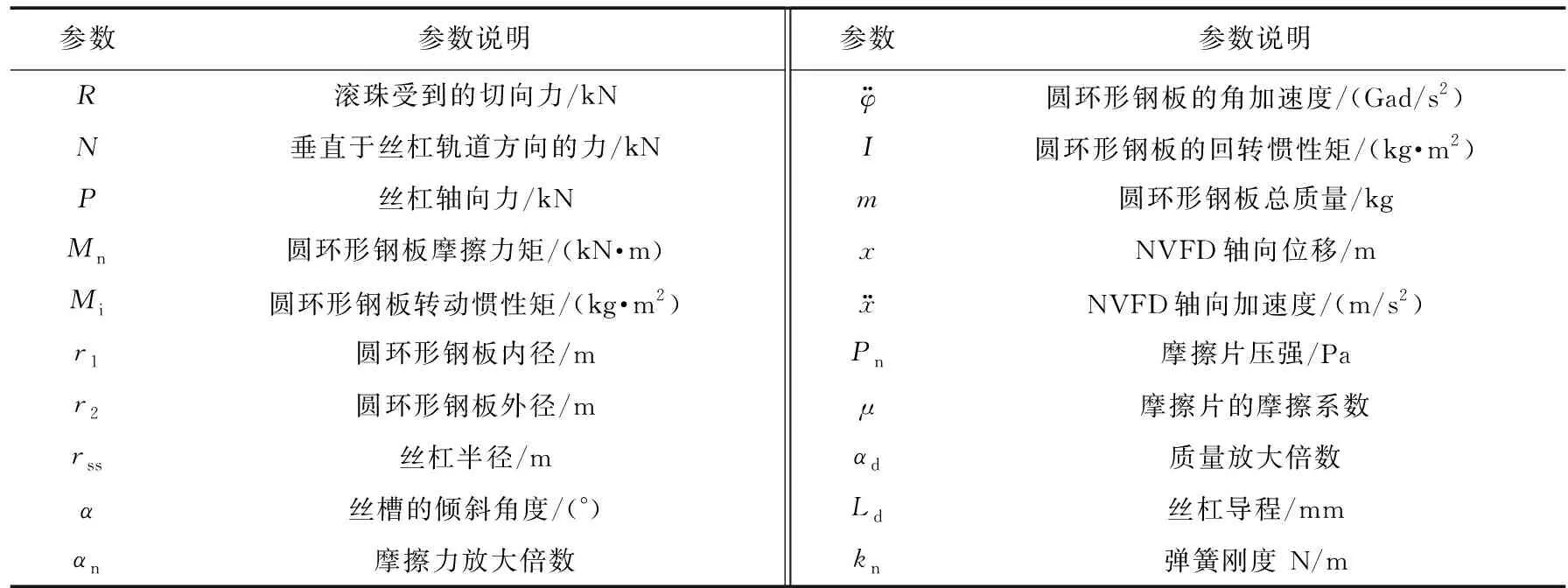
表1 参数符号表Table 1 Parameter symbols

图2 圆环形钢板受力分析图 图3 滚珠与丝杠力学分析图

参考文献[21]的公式推导,根据图2,对滚珠丝杠轴心点取力矩平衡有:

Rrss=Mn+Mi

(1)

根据旋转惯性质量单元的惯性矩进行计算,有:

(2)

(3)

(4)

摩擦片受到的压力为knx,则压强为:

(5)

微圆环切线方向上的摩擦力为:

(6)

微圆环的上摩擦力对圆心取矩,摩擦力矩为:

(7)

对r1-r2上积分得:

(8)

根据图3中的力学分析,可以得到:

(9)

式中:tanα=Ld/2πrss;η为滚珠螺母的实际工作传动效率,通过可达到90%～98%。

联立以上各式,得到丝杠轴向力的总表达式为:

(10)

(11)

(12)

摩擦力放大倍数为:

(13)

质量放大倍数为:

(14)

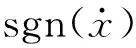
根据式(10)得出NVFD的恢复力模型,如图4(a)所示。NVFD往复滞回时,按照箭头所示的路径形成黑色实线所示的恢复力模型,由放大摩擦力形成的“蝴蝶型”曲线与正刚度效应的弹簧弹性力和负刚度效应的放大惯性力3个部分叠加而成。这是因为质量放大的倍数通常为成百上千倍,乘以实际加速度后得到负刚度效应的惯性力大于正刚度效应的弹性力,NVFD的恢复力模型在放大后的摩擦力形成的红色虚线恢复力模型基础上表现为负刚度效应加强,正刚度效应削弱,所以得到NVFD的理论完整恢复力模型如黑色实线所示。考虑到后续拟静力试验中,加载装置的加速度非常小,导致放大惯性力接近零,因此与拟静力试验对应的恢复力模型会表现为正刚度效应有所加强,负刚度效应有所削弱,如图4(b)所示。

图4 NVFD恢复力模型图Fig. 4 NVFD restoring force model diagram

2 拟静力试验研究

为了验证NVFD作用机理和恢复力公式的正确性,开展了拟静力试验研究,试验采用多通道电液伺服加载试验系统中的10 t级伺服作动器加载试验系统。该加载系统最大推压力量程为±100 kN,行程为±0.25 m,NVFD丝杠的位移和水平推压力可以通过作动器头自带的位移和力传感器进行自动记录。NVFD安装图如图5所示,为了保证作用器加载到丝杠上的水平推力为轴向力,本次试验在伺服作动器与NVFD之间连一个抗扭支座,圆环形钢板采用的材质为不锈钢,摩擦片为非石棉摩擦片,摩擦系数为0.35,弹簧刚度为15 kN/m,滚珠丝杠规格尺寸表见表2。

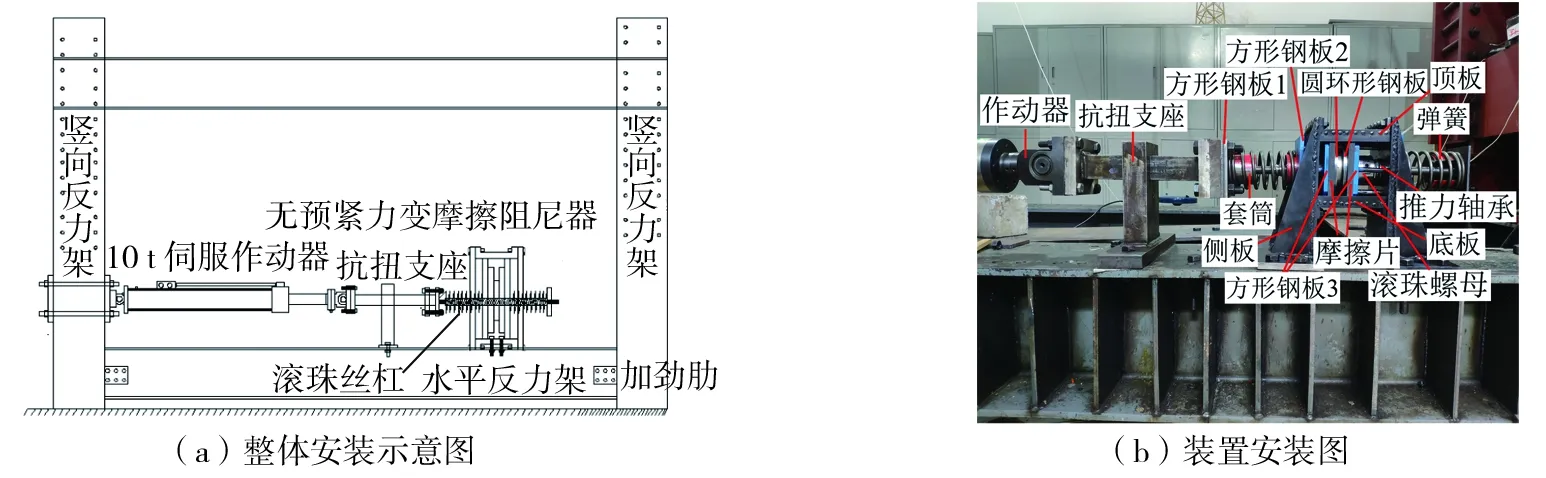
图5 试验安装图Fig. 5 Test installation drawing

表2 滚珠丝杠规格尺寸表Table 2 Specifications and dimensions of ball screw

试验采用正弦波位移控制加载,保持加载频率为0.003 Hz不变,加载幅值分别为40、60 mm,对应工况分别为S15-40-0.003和S15-60-0.003,每个工况循环加载3圈。因为滚珠螺母压紧推力轴承,圆环形钢板才能转动,导致试验加载力反向时,存在微小的滑移间隙,利用式(10)编制相同工况下考虑间隙的MATLAB程序,理论值和试验值对比如图6所示。各工况NVFD均呈“蝴蝶型”,理论值与试验值基本吻合,验证了NVFD作用机理和恢复力公式的正确性。丝杠力随弹簧的压缩量增加而增加,体现了其具有放大变摩擦力的特点。

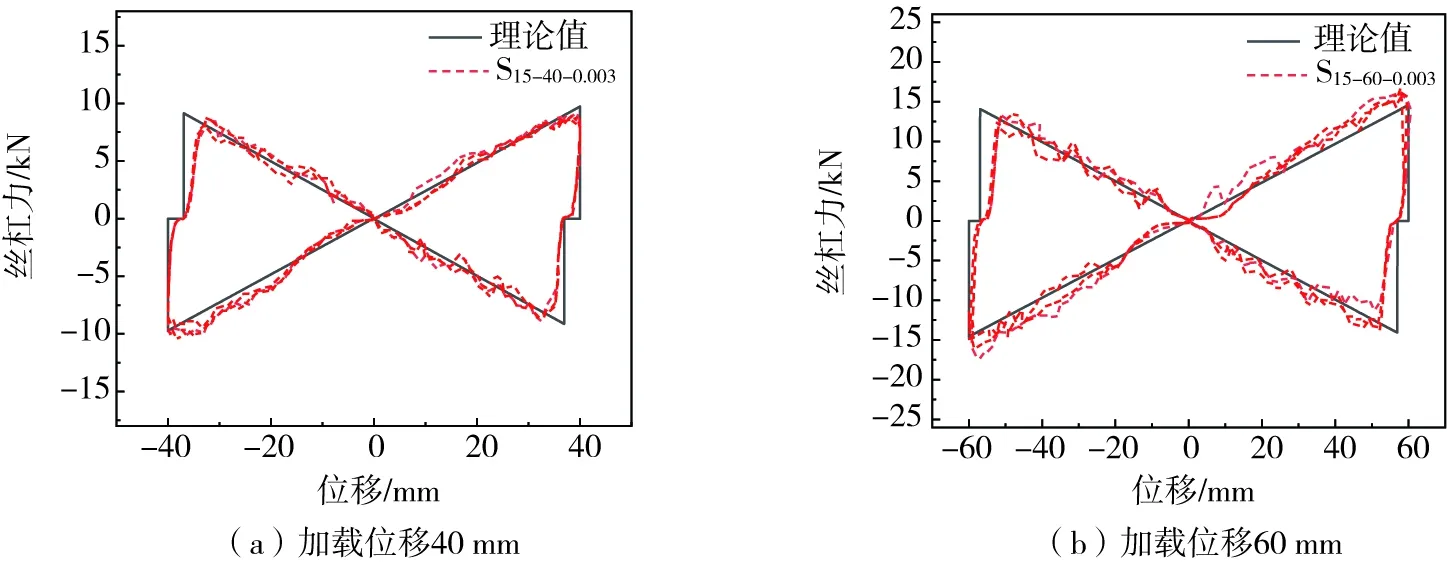
图6 理论与试验结果对比Fig. 6 Comparison of theoretical and experimental results

3 简谐激励下NVFD的SDOF动力特性分析

3.1 NVFD的SDOF位移解析解理论推导

附加NVFD的单自由度体系的分析简图如图7所示。

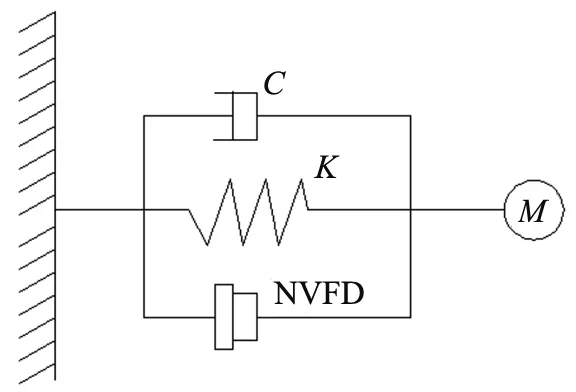
图7 NVFD单自由度体系简化分析模型Fig. 7 Simplified analysis model of NVFD single degree of freedom system

单自由度体系中附加NVFD,在外荷载作用下的运动方程为:

(15)

式中:M、K、C、x分别为单自由度结构的质量、刚度、阻尼系数和水平位移;P(t)为外部激励。在简谐激励下,假设NVFD处于连续滑动状态时,可以利用谐波平衡法求解NVFD单自由度系统的解析解。

令:

(16)

(17)

代入式(15)可得:

(18)

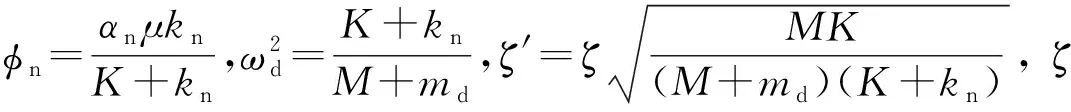
3.2 SDOF位移解析解的数值检验

通过采用四阶Runge-Kutta法编制的MATLAB单自由度程序对3.1节解析解进行数值检验。单自由度结构的模型参数如下:单层框架结构质量为M=40×104kg,刚度为K=5×106N/m,结构阻尼比为ζ=0.05;外部简谐激励荷载幅值P0=2M=80×104kN。NVFD的参数取值如下:μ=0.1,r1=0.1 m,r2=0.2 m。定义刚度比为γ=kn/K(弹簧刚度比结构刚度),质量比为β=md/M(放大后的圆环形钢板质量比结构质量),由式(10)知,刚度比和质量比的大小会直接影响NVFD的出力。下面将通过解析解和数值对比验证所推导的解析解的正确性,并分析刚度比和质量比变化对数值解和解析解吻合度的影响。

1)刚度比变化

取激励频率ω取值为2πrad/s,保持质量比为β为0.03不变,刚度比γ分别为0.06,0.09,0.12,0.18时,刚度比变化下数值解和解析解的位移时程曲线对比如图8所示。从图8中可以看出,在刚度比γ较小时,如γ=0.06、0.09时,解析解和数值解吻合的比较好,验证了解析解的正确性,随着γ的增大,二者结果的差别会逐渐变大。这是因为:随着γ的增大,NVFD的出力逐渐变大,外激励幅值保持不变的情况下,NVFD间歇性停止状态会变频繁,而位移解析解是基于NVFD一直处于滑动状态推导出来的,这种间歇性的停止状态增加了结构响应的高次谐波成分,影响了谐波平衡法的求解精度,导致二者结果的差别会逐渐变大。因此,只要NVFD参数取值合理,使得NVFD一直处于滑动状态,谐波平衡法推导的解析解具有较高的精度。

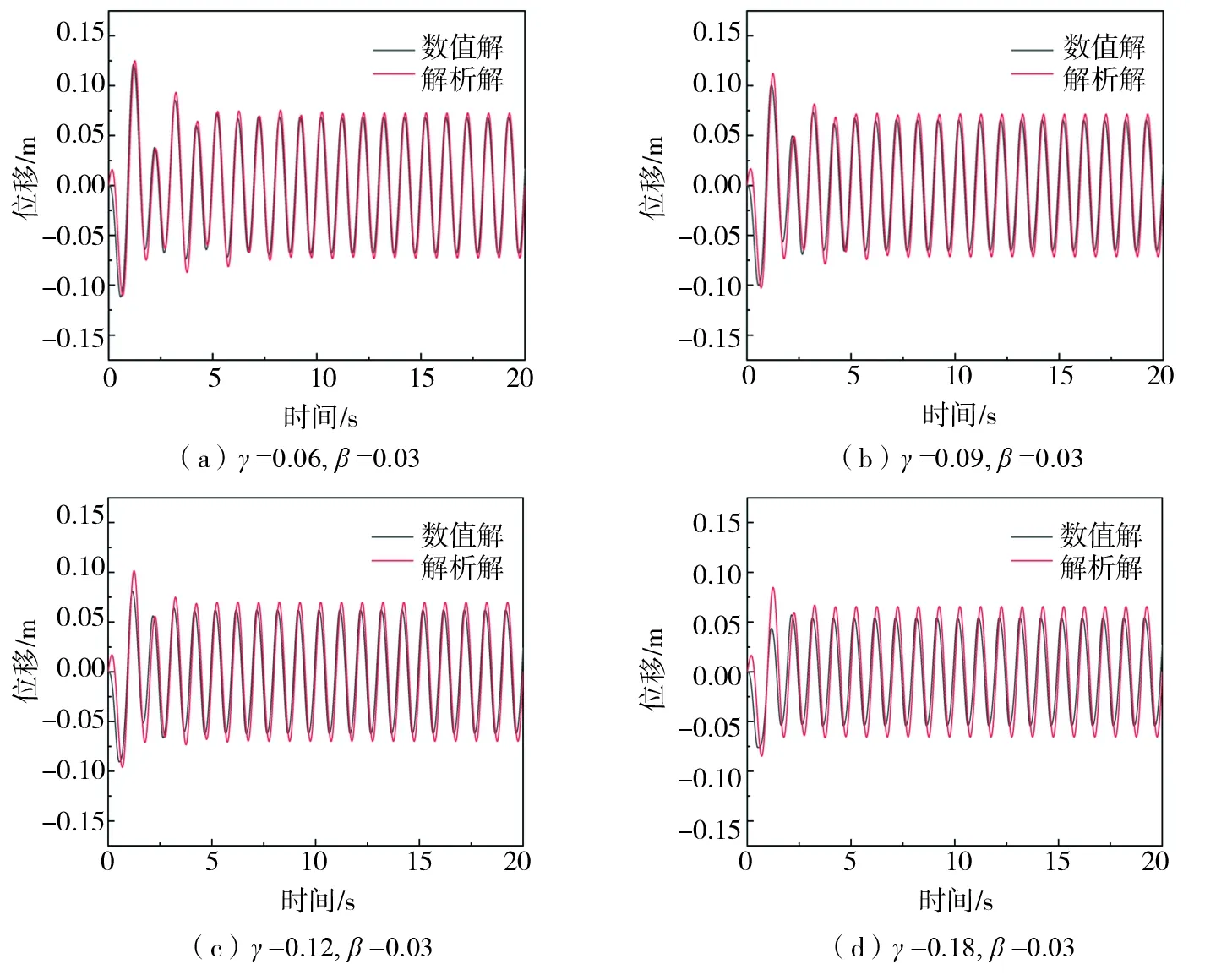
图8 不同刚度比下的数值解与解析解的对比Fig. 8 Comparison of numerical and analytical solutions under different stiffness ratios

由于以上的时程曲线是在特定外界激励频率下进行验证,为了避免偶然性,下面将进一步进行SDOF体系位移解析解和数值解的幅频响应分析。取激励频率ω取值为[0.5π, 4π],保持质量比为β为0.01不变,刚度比γ分别为0.01、0.02、0.03和0.06,取每个频率比下稳态反应对应的位移幅值,数值解和解析解的幅频响应曲线对比如图9所示。从图9中可以看出,和位移时程曲线结果类似,只要外界激励使得NVFD一直处于滑动状态,SDOF体系位移解析解和数值解的幅频响应曲线吻合得非常好,位移解析解误差很小。

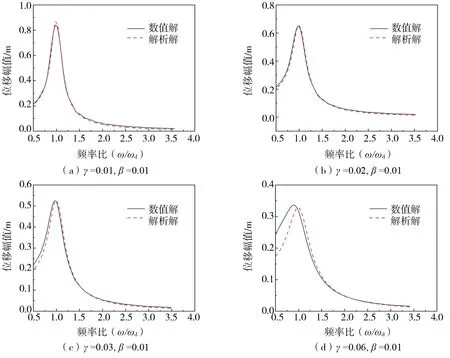
图9 不同刚度比下的幅频响应曲线对比Fig. 9 Comparison of amplitude-frequency response curves under different stiffness ratios

2)质量比变化

取激励频率ω取值为[0.5π, 4π],保持刚度比为γ为0.01不变,质量比β分别为0.01、0.03、0.06和0.12,质量比变化的数值解和解析解幅频响应曲线对比如图10所示。从图10中可以看出,在保持γ不变的情况下,在质量比较小时,如β=0.01、0.03时,位移解析解和位移数值解吻合的比较好,而当β=0.06、0.12时,解析解和数值解的误差越来越大,原因和改变刚度比相同,这里不再进行阐述。

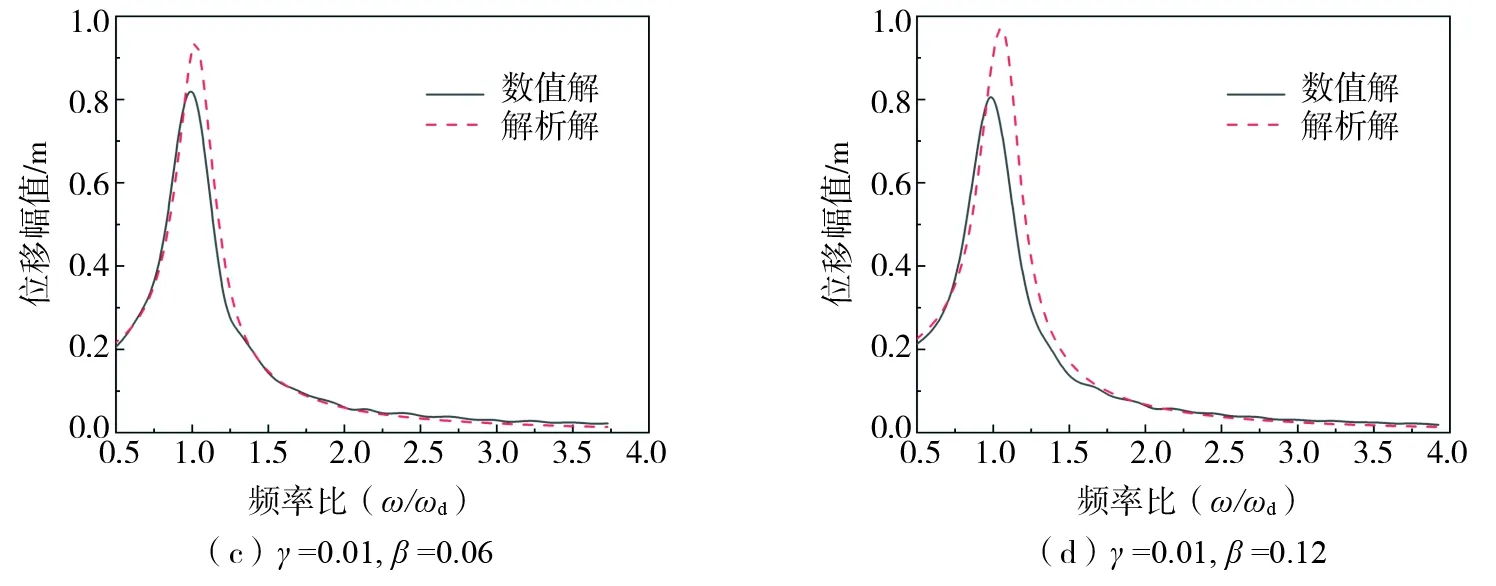
图10 不同质量比下的幅频响应曲线对比Fig. 10 Comparison of amplitude-frequency response curves under different mass ratios

3.3 NVFD的SDOF动力放大系数分析

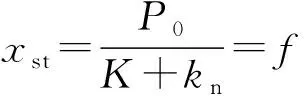
(19)

则动力放大系数为:

(20)

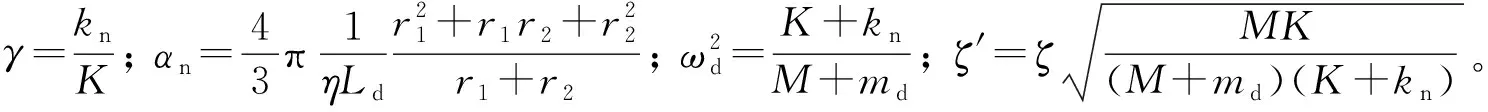
从式(20)可以看出,动力放大系数与NVFD的圆环形钢板质量、弹簧刚度、摩擦力放大倍数有关。下面将分别研究动力放大系数与这3个参数的关系。

1)动力放大系数与弹簧刚度和摩擦力放大倍数的关系

保持μ=0.2,αn=54.5,β=0.03不变,弹簧刚度kn=0、50、100、150、300 kN/m,对应的刚度比γ分别为0、0.01、0.02、0.03和0.06,得到不同刚度比下的动力放大系数,如图11(a)所示;保持γ=0.01,β=0.03不变,改变摩擦力放大倍数αn,得到不同摩擦力放大倍数下的动力放大系数,如图11(b)所示。从图11可以看出:在其它参数相同的情况下,频率比小于1.5时,附加NVFD单自由度结构的动力放大系数随着弹簧刚度和摩擦力放大倍数的增大而减小,在频率比大于1.5时,基本不受两者的影响,在频率比为1时减小效果最明显。

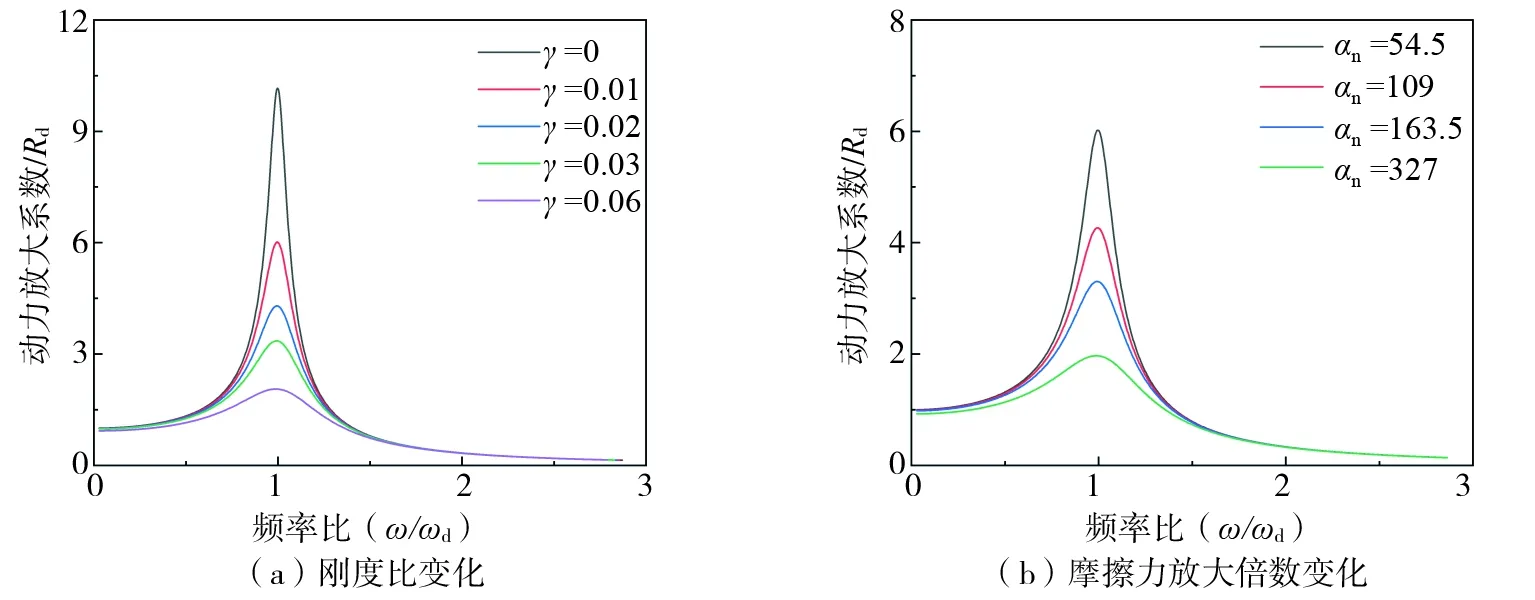
图11 刚度比和摩擦力放大倍数变化对动力放大系数的影响Fig. 11 Influence of stiffness ratio and friction damping force amplification on dynamic amplification coefficient

2)动力放大系数与放大后的质量的关系

保持μ=0.2,αn=54.5,γ=0.03不变,md=12×103、24×103、36×103、60×103kg,对应的质量比为0.03,0.06,0.09,0.15。从图12可以看出:在其它参数相同的情况下,在共振区域(ω/ωd=1)附近,动力放大系数Rd随圆环形钢板质量的增大而增大,其它部分基本不受NVFD圆环形钢板质量变化的影响。

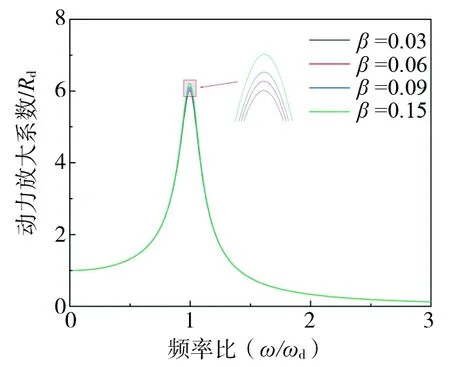
图12 质量比变化对动力放大系数的影响Fig. 12 Influence of mass ratio variation on dynamic amplification coefficient

4 结论

文中提出了一种无预紧力变摩擦阻尼器,具有无需施加预紧力即可提供变化的摩擦力的特点,且具有摩擦力、位移和惯性质量放大效应。通过工作机理介绍、恢复力公式推导和开展拟静力试验、位移解析解和动力放大系数的推导及相关参数分析,得出主要结论如下:

1)通过理论推导,给出了NVFD的恢复力计算公式和恢复力模型。

2)通过拟静力试验验证了无预紧力变摩擦阻尼器作用机理和恢复力公式的正确性。试验表明NVFD是一种位移相关型阻尼器,摩擦力随弹簧压缩量的增加而增大,具有放大变摩擦力的特点。由于拟静力试验无法体现放大质量的影响,后续将开展拟动力试验研究放大质量对NVFD摩擦力的影响。

3)利用谐波平衡法给出了在简谐激励作用下的位移解析解,利用4阶Runge-Kutta法推导数值解与解析解进行对比,并研究刚度比和质量比对2种解吻合程度的影响。结果表明:只要NVFD参数取值合理,在外激励作用下处于滑动状态,则2种解基本吻合,谐波平衡法推导的解析解具有较高的精度;反之,如果选取的参数让NVFD处于滑动和停止状态切换得较多,间歇性的固定状态增加了结构响应的高次谐波成分,则二者相别将会比较大。

4)推导了动力放大系数公式,并进行相应参数分析,结果表明:频率比小于1.5时,NVFD单自由度体系的动力放大系数随着弹簧刚度和摩擦力放大倍数的增大而减小,基本不受圆环形钢板质量变化的影响。