高桩承台桥梁概率洪水冲刷风险及时变抗震性能

吴文朋,药永娇,吴志伟,2,肖洋椰

(1. 湘潭大学 土木工程学院,湖南 湘潭 411105; 2. 保利长大工程有限公司,广东 广州 510620)

0 引言

对于跨越水域的桥梁结构,洪水冲刷引起基础侧向支撑变弱甚至失效是导致结构承载能力下降或垮塌的最常见原因[1]。例如,美国1966—2005年统计的1 502座倒塌损毁桥梁,其中有878座是由于冲刷导致的[2];哥伦比亚1986—2001年统计的63座桥梁事故,其中24%是由于洪水冲刷导致的[3]。我国在2000—2012年统计的157座桥梁垮塌事故,有45.86%是由于洪水冲刷导致的[4]。桥梁冲刷的实质是洪水对桥墩或桥台基础周边土层冲蚀剥离的动态过程,基础周围一旦形成局部冲刷坑洞,就会在桥梁的剩余使用寿命期内产生持续影响。如果未来发生更大的洪水,冲刷坑洞可能会变得更深,同时会进一步放大其它自然灾害对桥梁工程的不利影响,例如船撞、台风、地震等等[5-6]。

由于洪水冲刷的发生概率要远高于地震的发生概率,然而公路或铁路桥梁往往是地震灾难发生以后维持交通网络正常运行的枢纽。因此,国内外很多学者开始研究冲刷效应对桥梁抗震性能的影响。WANG等[7]通过振动台试验研究了基础冲刷对桩柱式桥墩抗震性能的影响;周敉等[8]建立了冲刷与地震联合作用下桥梁失效概率模型,研究了震区连续刚构桥冲刷作用组合的分项系数。PRASAD等[9]分析了不同大小洪水冲刷条件下的基础深度变化情况,并且针对4座不同规模的钢筋混凝土桥梁进行易损性分析。WANG等[10]指出应在桥梁抗震设计中考虑基础冲刷效应影响。以上研究均表明,洪水冲刷和地震作为2种常见的极端灾害事件,桥梁设计中要考虑二者联合作用的可能性,忽视冲刷效应会导致抗震性能评估结果不准确。

然而,需要指出的是,目前大量跨水域桥梁工程采用高桩承台式桥墩结构。一方面,这类多构件组合式桥墩结构的冲刷深度计算与传统简单独柱式桥墩的冲刷计算有所不同[11],因此,如何量化各构件对复杂桥墩冲刷深度的影响仍值得探讨。另一方面,洪水冲刷和地震2类灾害事件在同一时间发生的概率很小,既往研究中直接将多灾害联合作用施加于新建桥梁工程进行性能评估[10],主要是为了强调抗震设计中考虑洪水冲刷的必要性。然而,洪水冲刷和地震2类灾害事件相继发生的情况在历史上真实出现过[6],由于洪水冲刷是一个动态发展的过程,过程中涉及诸多不确定性,例如,桥址处河流水文信息和桩-土相互作用模型的不确定性等。因此,如何在分析桥梁服役期间的抗震性时考虑冲刷不确定性因素的影响仍然值得探讨。

文中首先介绍了高桩承台式桥墩的局部冲刷概率风险分析框架,以我国西部地区某跨河连续刚构桥为例,对桥址处河流的概率洪水危险性进行分析,基于冲刷分量叠加法构建了高桩承台式桥墩在不同年份洪水事件下的概率冲刷深度风险评估曲线;然后,建立OpenSees桥梁有限元分析模型,采用不断更新p-y土弹簧的方法模拟洪水冲刷对桩-土相互作用的影响,探讨了桥梁服役期间桥墩局部冲刷对算例桥梁动力特性和抗震性能的影响规律。

1 高桩承台式桥墩局部冲刷计算

1.1 确定性冲刷计算方法

桥墩局部冲刷是指由水流冲蚀基础周围土壤形成冲刷坑的过程,大量学者对桥墩局部冲刷进行试验研究[12-13]。基于水槽试验的冲刷研究多是针对简单桥墩,冲刷机理如图1(a)所示。对此各国学者分别提出过不同的冲刷深度计算式[11,14-15],其中应用较广泛的是美国HEC-18报告[11]推荐的基于CSU方程修正后的公式(简称“HEC-18公式”),该公式可被用来计算简单桥墩的最大冲刷深度:

(1)

式中:Ys、y0和V0分别为局部冲刷深度(m)、上游水深(m)和流速(m/s);a为垂直于水流方向桥墩宽度(m);K1、K2、K3分别为与桥墩形状、流水夹角以及流场条件相关的修正系数,HEC-18报告中[11]分别给出不同修正系数的建议取值;g为重力加速度(取g=9.8 m/s2)。

高桩承台式桥墩往往由墩身、承台和群桩等构件组成,通常是将下部结构简化成一个整体来计算局部冲刷效应[15]。由于墩身、承台和群桩等子构件均会以不同方式阻碍水流前进,美国规范建议采用冲刷分量叠加法(superposition of the scour components, SSC)[11]计算。实际上,SSC方法是在HEC-18公式基础上,通过对河道流速和深度、墩身和承台宽度、群桩高度和宽度等进行修正,然后单独计算墩身、承台、群桩3个分量的冲刷深度,最后相加得到冲刷总深度,如图1(b)所示。由于SSC方法有计算参数较少、过程简单且公式适用范围较广等优势,下面首先对墩身、承台、群桩3个子构件的冲刷深度分量计算方法分别进行介绍。

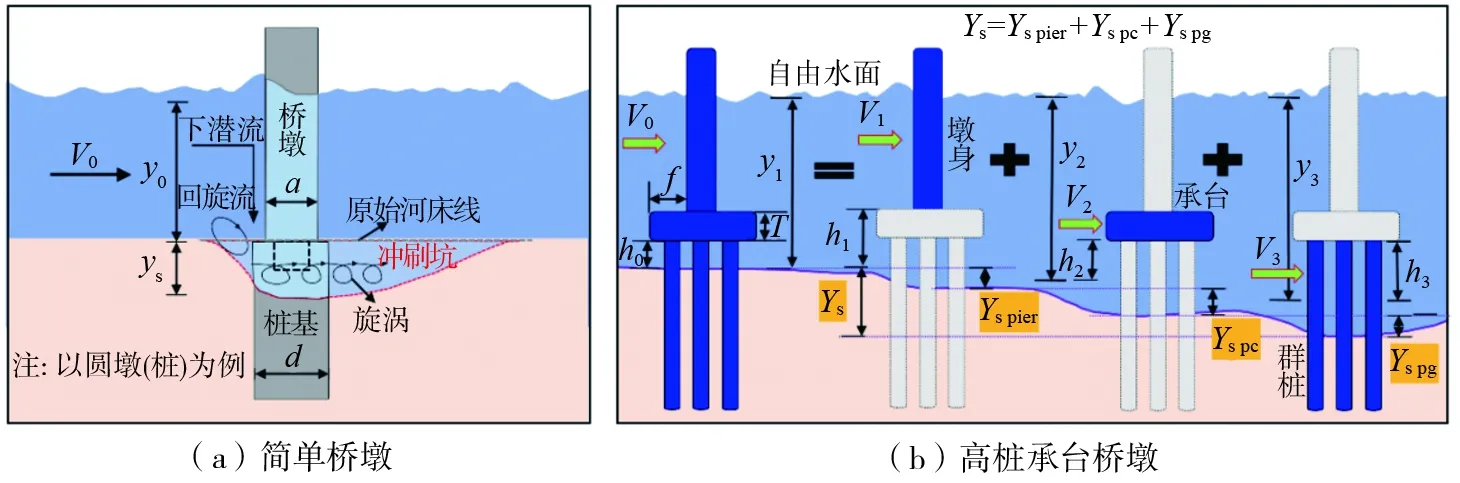
图1 桥墩冲刷机理及冲刷分量叠加法示意图Fig. 1 Diagram of simple pier scour mechanism and the SSC method

1.1.1 墩身部分局部冲刷分量

墩身部分局部冲刷分量是在HEC-18公式基础上引入修正系数Kh pier实现的:

(2)

式中:Ys pier为墩身局部冲刷深度分量(m);V1和y1分别为开始计算时桥墩上游流速(m/s)和深度(m);apier为迎水面墩身宽度(m),分别对应式(1)中V0、y0和a;Kh pier为墩身影响修正系数,HEC-18[11]直接给出了Kh pier与多组h1/apier和f/apier比值对应的曲线,一般情况下可通过式(3)计算:

Kh pier=(0.407 5-0.066 9f/apier)-(0.427 1-0.077 8f/apier)(h1/apier)

+(0.161 5-0.045 5f/apier)(h1/apier)2-(0.026 9-0.012f/apier)(h1/apier)3

(3)

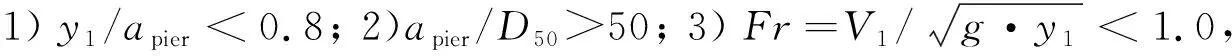
(4)

式中:Fr为水流弗劳德数;D50为河床颗粒中值粒径(m);Vc为D50泥沙临界启动流速(m/s)。

1.1.2 承台部分局部冲刷分量

承台底面始终高出河床和考虑墩身部分冲刷深度后导致承台底面高出河床,都属于高桩承台情况,分别如图2所示,此时可采用式(5)计算承台部分局部冲刷深度分量:

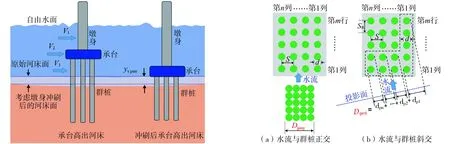
图2 底面高于河床情况的示意图 图3 不同水流情况下群桩投影宽度

(5)

(6)

1.1.3 群桩部分局部冲刷分量

群桩对冲刷的影响可分为水流与群桩正交和斜交2种情况,冲刷深度分量计算过程如下:

1)计算群桩的投影宽度Dproj

水流与群桩正交时,桩径d×群桩列数n便是群桩的投影宽度Dproj,如图3(a)所示。水流与群桩斜交时,先计算各桩投影宽度之和,再减去重叠区域宽度,如图3(b)所示。

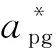
(7)

式中:Dproj为群桩投影宽度之和(m),见图3;Ksp为桩距系数;Km为群桩行数修正系数。一般情况下,Ksp与Km可通过式(8),式(9)计算得到:

Ksp=1-4/3[1-1/(Dproj/d)][1-(S/d)-0.6]

(8)

Km=0.9+0.1m-0.0714(m-1)[2.4-1.1(S/d)+0.1(S/d)2]

(9)

式中,S、d和m分别为桩间距(m)、直径(m)和行数,见图3。采用式(9)计算Km时需要注意的是,当m≥6时,Km不再随m变化而增加,且当水流与群桩斜交或者群桩交错排列时Km=1.0。

3)调整群桩的水流深度y3和来流流速V3

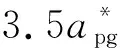
4)确定群桩高度调整系数Khpg

群桩高度调整系数Khpg可以表示为与h3/y3相关的函数,计算公式为:

(10)

5)计算群桩部分的冲刷深度分量Ys pg

修正后可得到群桩部分局部冲刷深度分量计算公式:

还有人说我们中国人爱嫉妒，美国人不这样。我20世纪80年代做访问学者到美国，发现美国人也嫉妒，男人、女人、黑人、白人、西方人、东方人都有嫉妒心理。

(11)

式中,各参数意义同前,修正系数K2=1.0是因为计算群桩宽度时考虑的是投影面积。

1.2 概率性冲刷计算方法

尽管以上公式为桥梁工程师提供了一种评估高桩承台式桥墩最大局部冲刷深度的确定性计算方法。然而,JOHNSON等[16]对多种桥墩局部冲刷方程计算的冲刷深度预测值进行对比后发现,HEC-18公式预测值与实测冲刷值相比较过于保守,主要原因是计算用到的水流流速、水深、河床泥沙粗糙度等参数具有很大不确定性。BOLDUC 等[17]的研究结果所表明,HEC-18公式计算得到的冲刷深度预测值与试验结果间存在41.3%～60.4%的误差。冲刷预测中存在的不确定性主要包括模型不确定性、水文不确定性和参数不确定性等[18]。目前,桥梁基础冲刷预测过程中的不确定性分析方法主要包括概率分析方法和可靠性分析方法[16,18]。其中,概率分析方法可以使用任何概率分布来表示冲刷效应,即可用一个具有均值、标准差的概率冲刷估计值来表示。实际桥梁设计中的其它类型的荷载,如船舶和车辆撞击、地震、风荷载等,均可作为概率荷载进行处理。因此,文中采用概率分析方法来评估和预测复杂桥墩基础局部冲刷深度是比较合适的。JOHNSON等[18]在HEC-18公式中引入模型修正系数,并假定部分参数为服从一定概率分布特征的随机变量,以此考虑各类不确定性对冲刷深度预测的影响,调整后的概率性冲刷深度预测公式如式(12):

(12)

式中:λs为模型修正系数;K4为与河床泥沙粒径相关的修正系数,其它参数意义同前。概率性冲刷分析中一般将水文信息的未来风险视为最主要的不确定性来源[17]。对于河流同一河道断面处,在不同流量的情况下,曼宁公式可以用来计算相应流量下的水深和流速,在给定流量和河流断面的情况下,文中假定河流断面为矩形时,则上游水流平均流速为:

(13)

式中:Q为河流流量(m3/s);W为河流宽度(m);上游水流深度y0可根据式(14)计算[19]:

(14)

式中:n为曼宁系数,自然河流取值通常为0.035;s为河道纵向坡度。式(12)～式(14)主要适用于简单桥墩,对文中的复杂桥墩,变换后的概率性冲刷深度预测公式如式(15)所示:

(15)

式中各参数的意义、单位以及各参数之间的关系同前文说明一致,可参照理解,此处不再赘述。

综上所述,只需要提供桥梁所在河道的几何参数和年洪水流量信息,就可以利用式(13)～式(15)计算得到指定洪水流量下的最大平衡冲刷深度。当式(13)～式(15)中的参数表示成随机变量时,可采用蒙特卡罗方法计算得到冲刷深度的概率估计。实际应用中可以根据具体情况来确定需要考虑的随机变量,文中参考既有的研究成果[10,18,20],共选取6个参数作为随机变量来进行概率冲刷深度评估,包括模型修正系数λs、流水夹角修正系数K2、河场条件修正系数K3、河流宽度W、曼宁系数n和河道纵向坡度s。以上6个参数的概率分布特性如表1所示,其它计算参数在文中均假设为定值。

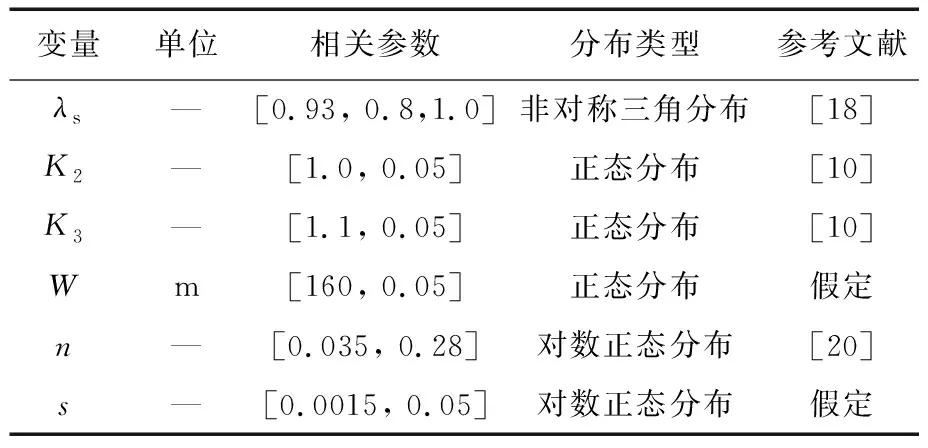
表1 用于冲刷深度评估的随机变量统计参数Table 1 Statistical parameters of the random variables used for the evaluation of scour depth

2 桥梁冲刷概率风险分析

2.1 算例桥梁介绍

算例桥梁为我国西部地区某跨河公路桥,桥梁全长310 m,总体跨径布置为(4×30)m+(50+90+50)m。引桥为四跨连续T梁桥,主桥为预应力变截面混凝土连续刚构桥,主梁截面为单箱双室,根部梁高6 m,跨中梁高2.3 m,为 C55全预应力混凝土结构;主墩为30 m高的双肢薄壁墩,承台尺寸19 m×9.6 m×4 m,材料C40;下部采用8根直径2.2 m的高桩承台群桩基础,材料C30。算例桥梁其它详细参数如图4所示,由于桥址处历史最高洪水位尚没有到达过渡墩位置,因此,文中主要以主桥结构为分析对象,即只考虑洪水对5#和6#主墩下部结构的冲刷情况。

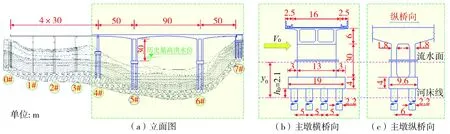
图4 算例桥梁结构布置图Fig. 4 Schematics of case-study bridge structure

2.2 洪水危险性分析

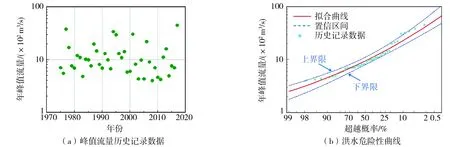
图5 桥位河流洪水危险性分析Fig. 5 Flood hazard analysis of the river crossing the bridge

log(Q)=μ+Kσ

(16)

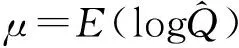
(17)

(18)

(19)

基于图5(a)中的历史水文数据,首先利用式(17)～式(19)计算μ、σ和g值,再利用这些统计参数估算洪水事件的发生概率K值,最后根据式(16)计算得到相应的年峰值流量Q值,从而可得到算例桥梁桥位处河流的洪水危险性曲线,如图5(b)所示。一般情况下,百年一遇洪水事件被认为是较严重的洪水事件,从图5(b)中所示的洪水危险性曲线中可以估算出100 a洪水(年超越概率为0.01)对应的流量为5 300 m3/s。此外,文中还考虑了1、5、10、20、50 a等发生频率更高的5次洪水事件,其年超越概率分别为0.99、0.50、0.10、0.05和0.02。从图5(b)中可以算出相应的年峰值流量Q分别为270、930、2 260、3 000、4 200 m3/s。需说明的是,由于文中的冲刷预测公式主要用于计算由单次峰值洪水流量决定的最大冲刷深度,无法考虑历年洪水冲刷的逐步冲刷累加效应,因此,文中给出的年份时间参数并非绝对的桥梁服役时间,而是采用桥址处河流洪水年超越概率对应的重现期来表示。

2.3 桥墩冲刷风险分析

利用表1中6个不确定性参数的统计特征,基于式(15)进行10 000次Monte-Carlo模拟计算和统计分析,可以得到在算例桥梁在不同年份的桥墩冲刷深度概率风险分析结果。

图6(a)以100 a 洪水为例,给出了桥墩冲刷深度的柱状图分布,包括墩身冲刷分量、承台冲刷分量、桩基冲刷分量和总冲刷的深度统计结果。由图6(a)可知,墩身对冲刷深度的影响很小,承台和群桩基础对冲刷深度的影响较大,这是由于算例桥梁所在河流100 a 的洪水流量并不大,导致高桩承台墩身淹没在水中的深度较小,即墩身与河床距离较远,对河床面冲刷的影响较小,因此,墩身局部冲刷深度的分量相对较小。针对其它不同年份的洪水冲刷深度分别进行Monte Carlo模拟计算,对超过给定冲刷深度的计算结果进行统计,然后除以总的模拟次数,可计算得到不同冲刷深度处的冲刷超越概率,即冲刷深度风险评估曲线,如图6(b)所示,分别给出了1、5、10、20、50、100 a的总冲刷深度风险曲线。由图可知,前20 a 内总冲刷深度的增加较明显,之后总冲刷深度的增加开始减慢。同时,以50%年超越概率对应的冲刷深度作为均值,表2列出了桥梁在不同年份各冲刷分量和总冲刷深度的均值。

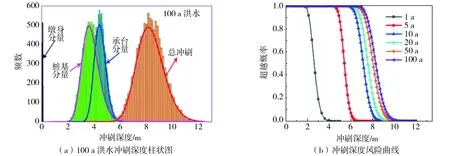
图6 冲刷危险性分析Fig. 6 Scour risk assessment

表2 主桥墩在不同时间的冲刷深度均值Table 2 Mean values of the scour depth for bridge pier at different years

3 OpenSees有限元建模

为分析概率冲刷作用对桥梁动力特性和抗震性能的影响,基于OpenSees程序建立了算例桥梁主桥的有限元分析模型,如图7所示。由于地震作用下主梁、盖梁和承台等构件一般不会发生破坏,故采用弹性梁柱单元模拟。水平地震力作用下桥墩和冲刷后群桩基础可能进入弹塑性阶段,故桥墩和桩基采用非线性纤维单元模拟,混凝土采用Concrete 04模拟,钢筋采用Steel 02模拟。同时,为准确反映地震作用下桥梁的真实受力,还对算例桥梁的支座、挡块、碰撞以及桥台系统的非线性效应进行了模拟,具体建模方法参考文献[22]。此外,文中采用OpenSees中的Py-simple1材料模拟桩-土非线性相互作用的影响。值得指出的是,上述建模过程没有考虑冲刷影响,当桥墩基础处河床土体逐渐被流水冲蚀剥落时,文中OpenSees模型中采用将冲刷深度(Hs)范围内p-y土弹簧移除的方法来模拟,如图8所示。

图7 算例桥梁计算模型Fig. 7 Analytical model of the case-study bridge

根据3.3节建立的桥墩基础冲刷深度风险评估曲线的均值结果,分别建立了7组OpenSees有限元分析模型,如表3所示。表中模型OSM1为对照组,为不考虑桥墩基础冲刷的情况,模型OSM2～OSM7分别对应不同年份冲刷情况下的OpenSees模型。需要指出的是,桥墩基础冲刷是动态发展的,由于冲刷导致的基础埋深不断减小(图8中h1,h2,h3的取值),而桩-土弹簧(p-y模型)的计算与弹簧所在的深度有关,因此,每次建立不同年份冲刷情况下的有限元模型时,需重新计算下部土层的水平约束,即考虑基础冲刷的每个分析工况模型都需重新调整和更新相应的桩-土弹簧模型。如图8所示,图中“0”表示基础尚未冲刷的情况,“i”表示第i个年份基础遭受洪水冲刷的情况,如表3所示,冲刷前桥梁有限元模型中采用(p-y)0弹簧模型,冲刷后桥梁有限元模型中则采用(p-y)i弹簧模型(i=1、5、…、100)。

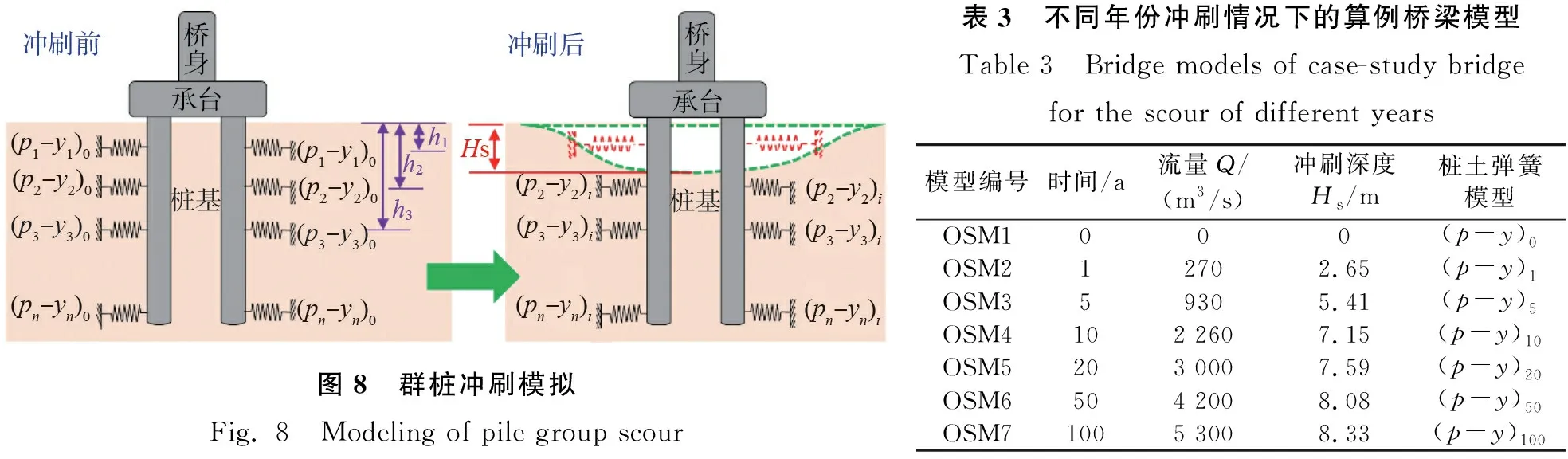
图8 群桩冲刷模拟Fig. 8 Modeling of pile group scour表3 不同年份冲刷情况下的算例桥梁模型Table 3 Bridge models of case-study bridge for the scour of different years模型编号时间/a流量Q/(m3/s)冲刷深度Hs/m桩土弹簧模型OSM10 00(p-y)0OSM212702.65(p-y)1OSM359305.41(p-y)5OSM4102 2607.15(p-y)10OSM5203 0007.59(p-y)20OSM6504 2008.08(p-y)50OSM71005 3008.33(p-y)100

4 冲刷桥梁动力特性分析

对不同年份冲刷情况下的桥梁模型分别进行动力特性分析,可得到前12阶模态周期如图9所示。由图可知,算例桥梁结构各模态振型对应的周期随着冲刷年份的增加而逐渐增大。

以图9中前3阶主要的模态振型为例进行说明。第1阶模态为全桥1阶纵向振动,结构周期由无冲刷时(OSM1)的T1=1.546 s增加到100 a一遇洪水冲刷时(OSM7)的T1=1.709 s,增幅为9.5%;第2阶振型为全桥一阶横向振动,结构周期由无冲刷时(OSM1)的T2=1.004 s增加到100 a一遇洪水冲刷时(OSM7)的T2=1.282 s,增幅达到21.6%;第3阶模态为全桥2阶横向振动,结构周期由无冲刷时(OSM1)的T3=0.976 s增加到100 a一遇洪水冲刷时(OSM7)T3=1.171 s,增幅为17.4%。在前12阶的模态振型中,第8阶模态的相对增幅最大(35.02%),这是由于群桩基础在该阶模态振型中的参与度最高。由图9还可发现,从0～10 a期间结构的周期变化幅值较大,而从10～100 a期间周期变化幅值较小,这是由于前10 a桥墩基础冲刷深度从0 m增大至7.15 m,相对增幅较明显,而随后90 a冲刷深度仅由7.15 m增大至8.33 m,相对增幅并不大。总体而言,随着桥梁服役时间增长,桥墩基础冲刷深度随之增加,桥梁模型各主要振型的周期也逐渐增大,且与基础冲刷深度大小呈正相关性。

图9 桥梁前12阶模态的周期变化比较 图10 地震波反应谱曲线

5 冲刷桥梁地震响应分析

5.1 地震波输入

文中按照我国现行的JTGT 2231-01—2020《公路桥梁抗震设计规范》[23]的建议,选取了7组地震波进行桥梁非线性动力分析,分析模型中采用纵向和横向同时输入地震记录的方法进行输入。7组地震波记录对应的反应谱曲线如图10所示。需要指出的是,后文均以7组地震波响应结果的平均值作为地震响应代表值,以分析桥墩基础冲刷对算例桥梁地震响应的影响规律。

5.2 主梁地震响应分析

图11(a)给出了主梁端节点最大位移随基础冲刷年份变化的关系曲线。由图可知,随着基础冲刷年份增加,主梁最大位移会随之而增加。从0增至100 a冲刷时,主梁纵、横桥向位移分别增加了5.5 mm和13.1 mm,冲刷前后最大增幅为9.58%,冲刷对主梁横桥向位移的影响大于纵桥向。

图11 桥梁位移比较Fig. 11 Comparison of bridge displacement

5.3 主墩地震响应分析

图11(b)给出了5#墩的墩顶和墩底节点最大位移随基础冲刷年份变化的关系曲线。由图可知,随着基础冲刷年份的增加,桥墩峰值位移也随之增大。从0增至100 a冲刷时,墩顶纵、横桥向位移峰值分别增加了5.6、21.9 mm, 冲刷前后最大增幅为19.38%;墩底纵、横向位移峰值分别增加了24.1、32.1 mm,冲刷前后最大增幅为130.98%。对于高桩承台桥墩基础,冲刷对桥墩横桥向位移的影响大于纵桥向,同时沿桥墩高度方向这种影响会逐渐变小。

图12给出了5#墩的墩顶和墩底截面最大内力(弯矩、剪力)随基础冲刷年份变化的关系曲线。由图可知,墩顶截面纵桥向的弯矩和剪力均随桥墩基础冲刷年份的增加而略有增加,例如,从0增长至100 a冲刷时,墩顶截面纵向弯矩增加了2 940.3 kN·m,增幅为4.8%,同时剪力增加了9.8%;然而,墩底截面纵桥向的弯矩和剪力均随基础冲刷年份的增加而有所减小,例如,从0增长至100 a冲刷时,墩底截面纵向弯矩减小了4.3%,剪力减小了11.1%。在桥墩墩底截面的横桥向,弯矩和剪力均表现为先增加后减小的规律,而且截面弯矩的这种变化规律更加明显。

图12 冲刷下桥墩内力比较Fig. 12 Comparison of pile internal force

5.4 桩基地震响应分析

图13给出了桥梁桩基沿深度方向各节点的最大位移随基础冲刷年份变化的关系曲线。由图可知,随着基础冲刷年份的增长,桩基0～20 m范围内的桩基变形有较明显的增加。从0增至100 a冲刷时,墩顶纵、横向位移峰值分别增长了20.2、31.7 mm,增幅为141%和113%。桥墩基础冲刷效应对于桩-土相互作用非线性效应的影响也十分明显。以主墩承台下的单根桩基距桩顶11 m处的土弹簧为例,在1#地震波作用下,其p-y滞回响应曲线随基础冲刷年份增长时的变化情况如图14所示。由图可知,随着桥墩基础冲刷年份增加,该深度处桩侧土体水平抗力随之减小,且土体变形逐渐增大,桩-土弹簧逐渐由弹性进入非线性。例如,从1增长至100 a冲刷时,土体抗力减小了28%,位移增加了265%。这主要是由于洪水冲刷效应使得土体被剥离冲走,冲刷线以上桩基失去侧向约束的同时,冲刷线以下的桩基由于埋深相对冲刷前有所降低,桩侧土体对桩基侧向约束减弱,从而导致桩周土体水平抗力下降,桩基变形增大。因此,跨水域桥梁进行抗震设计时有必要考虑冲刷效应对桩-土相互作用的影响。

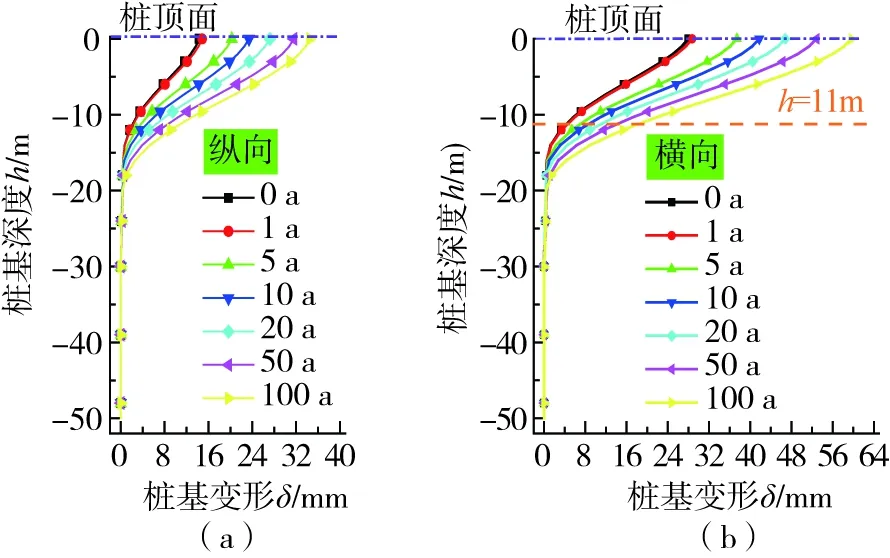
图13 桩基变形比较Fig. 13 Comparison of pier deformation

图14 1#地震波作用下桩基p-y土弹簧响应(h=11 m)Fig. 14 Seismic response of p-y soil spring under 1# ground motion (h=11 m)

6 结论

1)提出的概率性分析框架可以考虑各类不确定性的影响来建立高桩承台式桥墩基础的冲刷深度风险评估曲线。算例桥梁墩身冲刷分量对总冲刷深度影响很小,承台和群桩分量对总冲刷深度影响较大,且总冲刷深度变化在前10 a的增长较显著,随后的增长开始减慢。

2)随着桥墩基础冲刷年份的增长,高桩承台式桥梁结构前12阶振型周期、主梁和墩柱位移、以及墩顶截面最大内力均会逐渐增大,但桥墩墩底截面最大内力反而有所减小。

3)随着桥墩基础冲刷年份的增长,桩基0～20 m范围内桩基的变形会明显增加。桩侧土体的水平抗力随着冲刷深度的增加而减小,桩-土弹簧的非线性效应表现也会愈加明显,因此跨水域桥梁进行抗震设计时有必要考虑冲刷效应对桩-土相互作用的影响。

4)文中复杂桥墩局部冲刷深度概率分析方法主要考虑的不确定性因素是河道和水文参数的随机性,如何考虑其它类型不确定性的影响仍有待进一步研究。