爆炸荷载多尺度分析方法在仿真计算中的应用

陈龙明，李述涛，陈叶青，宝鑫

（1.军事科学院 国防工程研究院, 北京 100036；2.清华大学 土木工程系, 北京 100084）

研究岩土介质中爆炸对深埋地下结构的动力作用以及水中爆炸对舰船、大坝等装备或工程目标的破坏作用时，均涉及到介质中封闭爆炸问题研究，爆炸荷载产生的强冲击作用及介质动力响应涉及多材料、非线性的复杂耦合作用[1-3].相关理论研究较为复杂，目前多采用显式有限元方法进行数值模拟研究[4-5].爆炸近区产生的几何大变形是高频爆炸冲击波直接作用的结果[6]，数值计算需要设置满足截止频率的精细化网格来捕捉爆炸荷载中的高频成分，以提高计算精度.而显式时域逐步积分的最小时间步长受模型中最小单元尺寸限制，因此整体模型的计算效率较低.

随着大当量深钻地武器技术[7]的不断发展，越来越多的研究人员开展了爆炸荷载作用下的大范围工程场地动力反应研究[8].张月辉等[9]使用有限元方法对滨海软土中的爆炸过程进行了动力响应分析，总结了软土中不同爆炸量和埋深时爆炸冲击波的传播规律.YANG 等[10]通过建立全耦合的大规模欧拉-拉格朗日模型研究地表爆炸作用下土-结构-水的动力作用，研究发现地表爆炸将对浅埋引水箱涵的整体安全性造成极大威胁，并且水位会显著影响箱涵的动态特性.爆炸荷载作用下的大范围工程场地数值模拟研究中，爆源近区的精细化网格与大尺度整体模型尺度不协调[11]，存在着复杂异形网格过渡的难题.另一方面，较小尺寸的单元降低了满足显式时域逐步积分稳定性条件的临界时间步长[12]，导致计算成本增加，从而使得整体模型的数值计算难以高效完成.为解决该问题，李述涛等[13]提出了一种爆炸荷载多尺度分析方法，利用波场分解理论[14]及爆源子结构实现等效爆炸荷载的提取和输入，分步完成爆炸作用下大范围中远场地的动力响应分析，在保证计算精度的前提下大幅提高了计算效率.该方法需要在近爆源自由场模型计算基础上，构建爆源子结构模型，加载自由波场位移荷载，求解等效爆炸荷载并施加到大尺度中远场模型中.虽然在有限元软件中可以手动完成以上操作，但工作量较大且极易出错，也不便重复实施，不利于该方法的推广应用.

本文简要介绍爆炸荷载多尺度分析方法的基础理论，研究该方法在仿真计算中的应用技术.基于Python 语言环境自行开发一种k 文件处理程序，辅助完成建模和后处理工作，最后使用该方法对单爆源和多爆源2 种算例进行比对分析，给出适用性结论.

1 爆炸荷载多尺度分析方法

爆炸荷载多尺度分析方法基于波场分解理论，利用爆源子结构模型，将爆炸近区的自由场节点运动转化为节点反作用力，提取并施加于大尺度目标模型中，在完成等效爆炸荷载加载的同时实现网格尺寸过渡[13].操作流程主要分为3 个步骤，具体见图1.

图1 爆炸荷载多尺度分析方法示意图（1/2 模型）Fig.1 Schematic diagram of multi-scale analysis method of explosion load (1/2 model)

步骤1 求解近爆源区域的节点运动.建立爆源小尺度模型，设置精细化网格，获取近爆源区域节点位移时程数据，并在爆源小尺度模型中选取一定间隔的节点构建爆源子结构模型.最后提取子结构模型外2 层节点所对应的近爆源区域节点位移数据.

步骤2 通过爆源子结构将位移荷载转化为节点反作用力荷载.将位移数据按空间对应位置加载到爆源子结构节点上，进行动力分析后提取内侧2层节点的节点反力（reaction force）.

步骤3 对大尺度目标模型进行动力计算.建立大尺度网格目标模型，在空间坐标与子结构重合的节点上施加上一步提取到的节点反力，即爆源产生的等效爆炸荷载.通过动力计算获得大尺度模型在爆炸荷载下的动力响应.

2 爆炸荷载多尺度分析方法应用

爆炸荷载多尺度分析方法理论清晰、方法简便，可在仿真计算中应用.以岩土中封闭爆炸为例，以下详细介绍多尺度分析方法在仿真计算中的应用方法.

2.1 黏弹性人工边界单元的设置

应用多尺度分析方法研究岩土中的封闭爆炸问题时，首先需获得爆源附近的自由场节点位移荷载，合理地解决爆源小尺度模型的边界反射问题是实现多尺度方法的基础.本节主要介绍一种无反射边界-黏弹性人工边界在仿真计算中的设置方法.

在模拟半无限岩土地下封闭爆炸过程中可通过在截断边界位置施加人工边界条件，防止四周外行的地冲击波在边界处反射影响计算结果.常见的人工边界方法包括边界元方法、透射边界[15]、黏性边界及黏弹性边界[16-17]等.基于柱面波理论和球面波动理论[18]，刘晶波等[19]及谷音等[20]提出的一致黏弹性人工边界和等效边界单元提供了一种操作简便、效果良好的无反射人工边界方法.利用普通有限元单元在边界截断处构造黏弹性边界单元模拟黏弹性边界，该人工边界单元具备良好的吸波效果.李述涛等[21]详细介绍了黏弹性人工边界单元在ABAQUS中的实现方法，在仿真计算中使用可以参考此文献.李述涛等[12，22]介绍了黏弹性人工边界单元显式时域逐步积分稳定性的分析和改善方法，给出了边界单元厚度和最小时间步长的确定方法.在近爆源小尺度模型中，通常包含炸药、空气和岩土介质.炸药和空气域使用欧拉网格建模，空气域边界设置为无反射边界；岩土介质采用拉格朗日网格建模，在截断边界处设置人工边界单元.建立黏弹性人工边界时需在模型最外层延伸一层网格，二维和三维的人工边界单元如图2 所示.

图2 人工边界单元示意图Fig.2 Schematic diagram of artificial boundary element

黏弹性人工边界单元的具体设置如下：

①建立实体模型，划分网格后选中模型截断边界处的最外层网格单元，将其划分到单独的集合.人工边界单元应尽量划分为规则的四边形/六面体单元.

②选中人工边界的最外层节点，建立节点集合，对该节点的所有运动自由度进行约束.

③在线弹性材料模型中设置边界单元的等效弹性模量、密度以及泊松比.有限元计算中，若边界单元质量为0，会导致显式算法稳定性下降[12，22]，因此将边界单元的材料密度设置为较小的值，设置泊松比为0，同时输入等效弹性模量.在阻尼设置模块下输入等效阻尼，此处采取以时间为单位的瑞利阻尼形式.等效弹性模量和等效阻尼的计算方法可参考文献[19 - 20].

2.2 多尺度方法实施步骤

以LS-DYNA 为例，多尺度分析方法的实施步骤如下：

①建立小尺度的近爆源模型，如图3 所示.模型包含4 个PART，分别为炸药、空气、介质（土）和人工边界单元，流体和固体介质使用流固耦合算法实现力学参量的传递.

图3 近爆源模型Fig.3 Near-source model

近爆源模型建立完成后，再确定爆源子结构的空间位置：在炸药四周选择一个适当的正方形（二维）/正方体（三维）区域，“跳跃”式选取近爆源自由场模型中的节点，建立一个由2 层单元和3 层节点组成的爆源子结构模型，见图4.找到近爆源模型中与子结构外2 层节点空间坐标一致的节点编号，按k 文件格式写入关键字*DATABASE_HISTORY_NODE 模块下，并在代码中储存为列表Node1.该步骤旨在建立需要提取位移的节点集合，便于在计算输出文件中快速获取以上节点位移数据.

图4 爆源子结构模型Fig.4 Substructure model of explosion source

②处理近爆源模型输出的位移数据.对近爆源模型进行动力流固耦合计算后，将记录着Node1 中节点位移数据的结果输出文件转化输入到Excel 文件中.分别将各个分量的位移数据储存在不同的工作表（Sheet）中，二维时每个Excel 文件中有x、y2 个工作表，三维时每个Excel 文件中则有x、y、z3 个工作表.每个工作表中第一列数据为时间，其余列则为各个节点与时间相对应的位移，节点数据按节点编号递增排列.

③确定子结构节点与近爆源模型对应节点的空间对应关系.在近爆源模型k 文件*NODE 模块下，记录列表Node1 中节点的坐标值.然后在爆源子结构模型k 文件的*NODE 模块下，找到与Node1 中节点坐标值相同的节点，记录其编号，储存为列表NodeSet1.此步骤为后续加载节点位移数据做准备.

④在爆源子结构模型中加载自由波场运动.固定最内侧一层节点，将近爆源自由场中提取的节点位移数据（Node1）按对应关系加载到列表NodeSet1中的节点上.二维模型每个节点有x、y2 个方向分量，三维模型则有x、y、z3 个方向分量.使用关键字*BOUNDARY_PRESCRIBED_MOTION_NODE 对指定编号节点加载位移数据，通过关键字*DEFINE_CURVE 定义数据的时程曲线.首先将Excel 文件中的节点时程数据按规则转化到*DEFINE_CURVE_TITLE 模块中.例如写入第1 889 593 号节点x和y方向位移时程曲线的语句如下：

随后按照步骤③建立的节点对应关系写出*BOUNDARY_PRESCRIBED_MOTION_NODE_ID 关键字及其内容.例如对第1 889 593 号节点加载x方向和y方向位移语句如下：

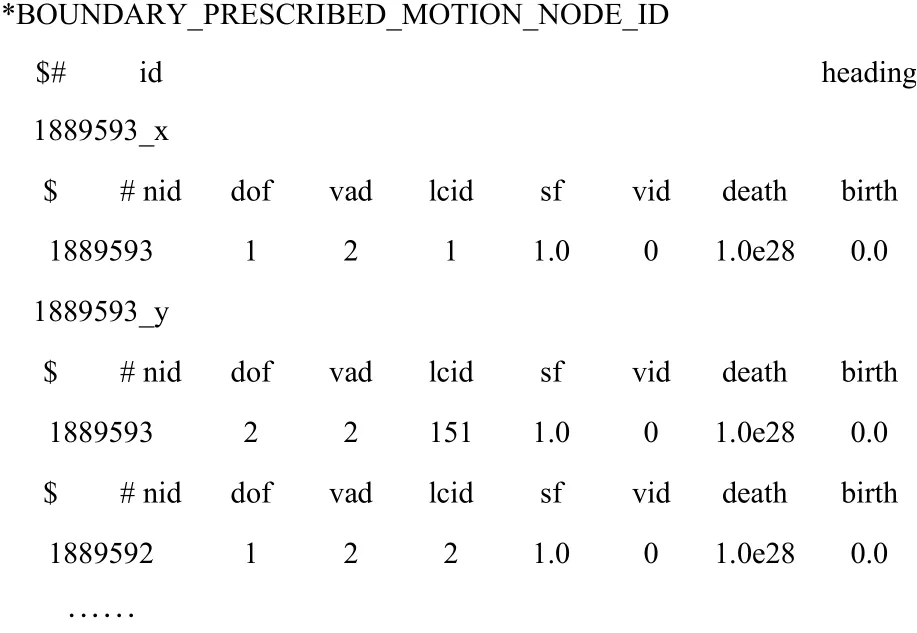
将2 个模块输出为单独的k 文件，最后在爆源子结构k 文件中利用关键字*INCLUDE 调用以上2 个模块即可实现位移加载.

⑤设置子结构模型中的节点力输出.选取子结构内2 层节点，定义为新的节点集*SET_NODE.利用关键字*DATABASE_NODAL_FORCE_GROUP 定义输出节点力的集合与坐标系.最后在*DATABASE_NODFOR 中定义节点力的输出间隔，完成节点反力的输出设置.求解内侧2 层节点的反作用力时，因读写的数据量较大，应设置合理的数据输出间隔，在保证输出曲线光滑的同时减少处理的数据量.

⑥处理子结构模型输出的节点反力数据.对爆源子结构模型开展动力计算后，利用后处理软件将记录着节点集*SET_NODE 模块中节点反力的数据文件转化输入到Excel 文件中，将*SET_NODE 中的节点储存为列表Node2.分别将各分量的节点力数据储存在不同的工作表（Sheet）中，二维时每个Excel 文件中有x、y2 个工作表，三维时每个Excel 文件中则有x、y、z3 个工作表.每个工作表中第一列为时间，其余列则为各个节点的节点反力.此节点反力即下一步加载于介质-目标模型的等效爆炸荷载.

⑦确定大尺度模型中加载等效爆炸荷载的节点与子结构节点的空间对应关系.根据子结构单元尺寸建立大尺度介质-结构模型，如图5 所示，并在截断位置处设置人工边界单元.介质-结构模型的网格尺寸与子结构网格尺寸需保持一致.在介质-结构模型中寻找与子结构模型内侧2 层节点坐标值相同的节点以加载节点反力.具体流程如下：首先在子结构模型k 文件的*NODE 模块下，记录列表Node2 中节点的坐标值.然后在大尺度介质-结构模型文件的*NODE 模块下，找到与Node2 中节点坐标值相同的节点，记录其编号并储存为列表NodeSet2.此步骤是为后续加载节点反力数据做准备.⑧在大尺度介质-结构模型中加载等效爆炸荷载.通过关键字*LOAD_NODE_POINT 对列表Node-Set2 中的节点加载力-时程数据.通过关键字*DEFINE_CURVE 定义数据的时程曲线.首先将Excel 中的节点时程数据按k 文件格式写入*DEFINE_CURVE_TITLE 模块中.例如写入第1 888 886 号节点x和y方向位移时程曲线的语句如下：

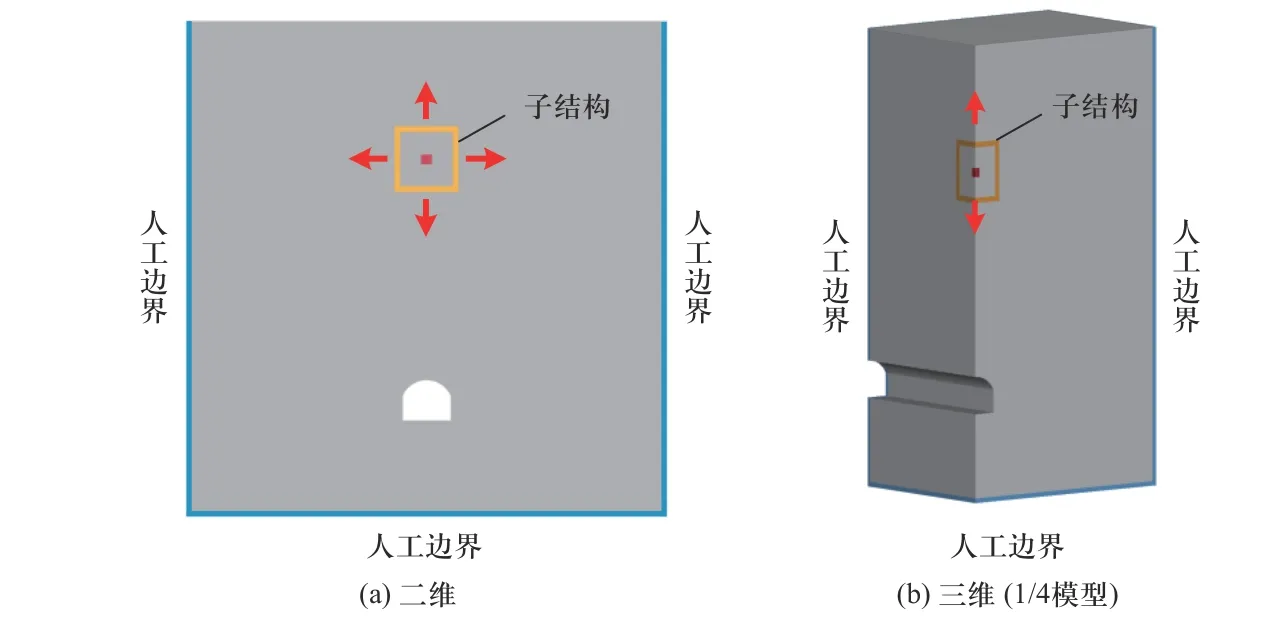
图5 介质-结构目标模型Fig.5 Medium-structure model

随后按照步骤⑦建立的节点对应关系写出*LOAD_NODE_POINT 关键字及其内容.例如对第1 888 886 号节点加载x方向和y方向节点力语句如下：

将2 个模块输出为单独的k 文件，最后在大尺度介质-结构k 文件中利用关键字*INCLUDE 调用以上2 个模块即可实现等效爆炸荷载加载.

2.3 编程的处理流程

由于多尺度方法需要比对和读写大量空间节点数据信息，如2.2 节中的步骤③④⑦⑧，特别是三维模型，涉及的数据量庞大，若全部由人工手动操作难度极大.Python 语言简单易读、功能强大，因此利用该语言自编程序对仿真计算关键字文件进行自动改写，可简单快捷实现上述步骤.为便于理解实施流程的逻辑关系，结合上一节的实施步骤，本节给出了编程的处理流程，如图6 所示.

图6 编程处理流程图Fig.6 Programming process flow chart

处理流程大致分为3 部分，各部分的标志环节分别为近爆源模型、爆源子结构模型和大尺度模型的有限元分析.在处理流程中，工作量较大的环节分别为比对节点坐标值、写入数据以及输出加载位移/节点反力的关键字.通过自编程序来解决这些问题，例如可通过条件循环语句来比对节点坐标值，使用循环语句批量输出加载位移/节点反力的关键字模块.给出的处理流程中，仍有部分环节需手动操作，例如设置指定节点的集合等，但这些环节的工作量和操作难度都较小.图6 中人工操作难度大的环节都通过自编Python 程序进行处理，极大地降低了多尺度分析方法在有限元软件中应用的操作难度.同时也应当指出，除Python 语言外，也可利用其他程序语言进行编程处理，例如C 语言、Fortran 语言等，本节仅提供编程处理的思路.

3 多尺度方法的应用算例

隧道开挖等工程实践中需分析地下封闭爆炸对深部地下结构和地表建筑的影响，本节应用多尺度方法分别研究地下结构在单个爆源荷载作用下的动态响应和地表桥梁结构在多个爆源荷载作用下的动态响应.

3.1 算例1：单个爆源作用于地下隧道

应用本文的实现方法建立二维半空间单爆源地下封闭爆炸计算模型，计算区域为180 m×180 m 的平面，如图7 所示.对模型进行均匀网格划分，网格尺寸为25 cm，单元总数为51.6 万个.同时使用普通建模方法建立了同规模的对比计算模型，近爆源区域采取网格过渡，炸药与介质之间采取流固耦合方法实现相互作用.爆源区域进行网格细化，远离爆源区域采用均匀网格划分，两者之间采取渐变网格过渡，最小网格尺寸为2 cm，最大网格尺寸为25 cm，单元总数为74.8 万个.爆源位于地下66 m 深处，装药为TNT，使用JWL 状态方程，材料模型选取为*MAT_HIGH_EXPLOSIVE_BURN.介质为弹性材料，材料模型选取为*MAT_ELASTIC，并按2.1 节的方法设置人工边界.具体材料参数参考文献[13].

图7 单爆源地下封闭爆炸二维模型示意图Fig.7 2D model of a single-source underground closed explosion

在相同计算条件下完成计算，普通方法计算耗时322 min，多尺度方法耗时44 min.图8 为多尺度方法算例和普通建模方法算例的位移场演化云图.在使用多尺度方法的算例中，应力波刚开始传播时，子结构对应的内部方形区域的节点位移为0，随着应力波向外传播，两者位移云图趋于一致.当t= 0.130 s时，除爆心区域外，应力波的位移云图结构基本相同.当t> 0.130 s 时，位移云图的结构差异已不明显.

图8 二维介质-结构模型位移云图Fig.8 Displacement of 2D medium-structure model

图9 为测点A和B在2 种建模方法下测到的节点位移曲线.图9 中，两者的位移时程曲线基本吻合，在单爆源的情况下多尺度分析方法可获得与普通建模方法相同的计算精度.

图9 测点A、B 位移时程曲线对比Fig.9 Comparison of displacement curves of A and B

3.2 算例2：多个爆源作用于地表桥梁

应用本文的实现方法建立二维半空间多爆源地下封闭爆炸计算模型，计算区域为110 m×340 m 的平面，地表处为桥梁横截面，如图10 所示.对模型进行均匀网格划分，网格尺寸为25 cm，单元总数为60.6万个.同时使用普通建模方法建立了同规模的对比计算模型.爆源区域进行网格细化，远离爆源区域采用均匀网格划分，两者之间采取渐变网格过渡，最小网格尺寸为2 cm，最大网格尺寸为25 cm，单元总数为130.3 万个.桥梁结构材料模型为*MAT_RHT，其余材料模型及计算条件同算例1.

图10 多爆源地下封闭爆炸二维模型示意图Fig.10 2D model of multiple sources underground closed explosion

在相同计算条件下完成计算，普通方法计算耗时537 min，多尺度方法耗时31 min.图11 为分别为多尺度方法算例和普通建模方法算例的位移场演化云图.在使用多尺度方法的算例中，应力波刚开始传播时，子结构对应的内部方形区域的节点位移为0，随着应力波向外传播，两者的位移云图差异减少.应力波作用于桥梁结构时，产生反射、绕射等现象，桥梁结构因爆炸荷载作用而产生不均匀的位移分布.由图11（c）和11（f）可知，桥梁产生的位移响应结果基本一致，表明在多爆源的算例中多尺度方法与普通方法的计算效果吻合得较好.

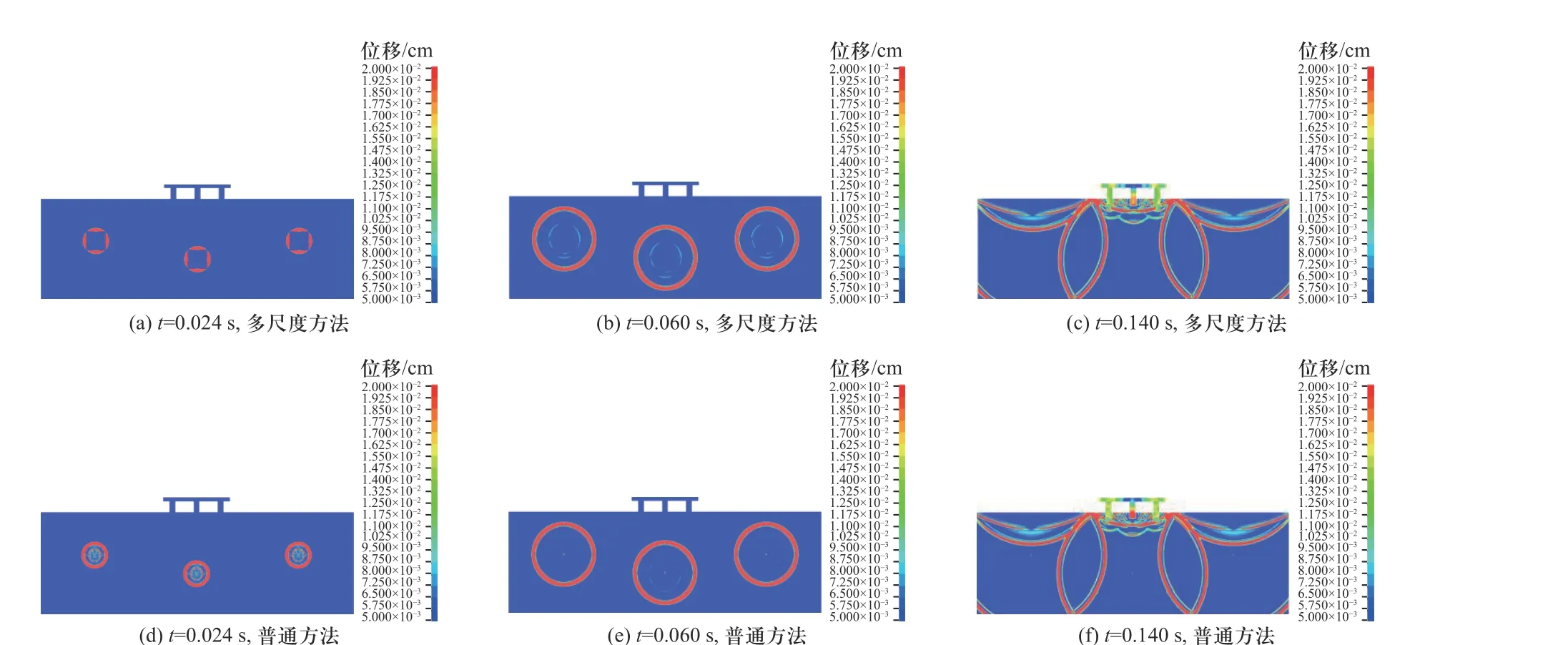
图11 二维介质-结构模型位移云图Fig.11 Displacement of 2D medium-structure model

图12 为测点C和D在2 种建模方法下测到的节点位移曲线.图12 中，两者的位移时程曲线基本吻合，在多爆源的情况下多尺度分析方法可获得与普通建模方法相同的计算精度.

图12 测点C、D 点位移时程曲线对比Fig.12 Comparison of displacement curves of C and D

多尺度方法在单爆源和多爆源的算例中均能获得与普通方法基本相同的计算效果，且计算效率远高于普通建模方法.爆源条件相同时，利用本文提出的操作方法可避免重复计算近场爆炸荷载，便于获得大批次相似算例的计算结果.以上的研究结果表明，与普通建模方法相比，在有限元软件中应用多尺度方法计算地下封闭爆炸模型具有突出的优势.

4 结 论

针对基于爆源子结构的爆炸荷载多尺度分析方法在仿真计算中存在一定的应用困难问题，本文简要介绍了该方法的基本理论，研究了该方法在仿真计算中的应用技术，对单爆源和多爆源2 种算例进行了对比分析.具体结论如下：

①基于爆源子结构的爆炸荷载多尺度分析方法可以较好地应用于大当量爆炸荷载作用下的大范围工程场地动力响应计算.在保证计算精度的前提下，计算效率显著优于炸药-介质-目标整体计算模型.

②对小尺度爆源模型进行一次计算，即可形成一个参数化的标准荷载，快速加载到介质中的任意位置.对于爆炸荷载位置变化或多爆源情况下的大范围工程场地动力计算问题，不必重复建模，避免对炸药爆炸过程进行低效率的流固耦合计算，大幅提高计算效率.

③建模计算中，需要应用基于Python 的自编程序实现空间节点坐标和数据信息的比对和读写.该程序逻辑清晰，可快速读写大批量数据文件，减少了人工操作可能带来的数据错误，极大地提高了模型前处理效率.