顺层高边坡双平面破坏分析方法研究
于群群,孙朝燚
(1.中电光谷建筑设计院有限公司,湖北 武汉 430000;2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,湖北 武汉 430071)
0 引 言
岩质边坡受原生作用或构造作用,坡内存在节理、断层等不连续结构面。在结构面的切割作用下,岩质边坡被分为块状边坡、层状边坡、碎裂状边坡和散体状边坡[1]。顺层边坡是指节理产状和坡面产状近似一致的一类层状边坡,广泛存在于交通、水电和矿山等基本工程建设领域。
顺层高边坡由于坡内结构面发育,在降雨、地震或人工开挖条件下[2-8],顺层节理和缓倾节理容易贯通,产生双平面滑动破坏,形成大型滑坡,如天台乡、千将坪和鸡尾山滑坡等[8-10]。
顺层高边坡双平面滑动破坏深度深、规模大,潜在危害巨大。陈晓磊[11]利用极限平衡原理推导了双滑面边坡在水力条件、坡顶堆载和地震效应综合作用下的稳定性系数表达式,但公式形式较为复杂;陈龙龙[12]采用极限平衡方法分析了两组结构面交作用下的节理边坡稳定性;C.Sun等[13]和M.Havaej等[14]对顺层高边坡的双平面贯通全过程进行了数值演化,并提出了双平面滑坡的柱状力学模型;L.R.Alejano等[15]通过理论分析、物理模型、数值模拟等手段开展了露天矿下盘顺层边坡的破坏机理探究,并提出了一种计算边坡安全系数的建议方法;L.Chen等[16]提出了双平面岩质边坡稳定性图表分析方法,并研究了边坡安全系数在不同影响参数下的变化规律;C.Sun等[17-18]基于顺层岩质高边坡主动块和被动块力学作用原理,提出了极限平衡分析方法,并研究了坡脚堆积物的稳定性影响规律。
这些文献促进了顺层高边坡双平面滑动研究的发展,增加了相关学者和工程实践者对该类破坏的认识和思考。但是多数学者提出的边坡安全系数计算公式或图表分析均较为复杂,不利于工程实践的使用和推广。
1 双平面滑体模型
基于顺层高边坡双平面滑动机制,滑体可分为主动块和被动块[15-18]。本文假设条块分界面方向竖直,根据主动块和被动块底滑面交点与坡肩点的位置关系,其几何模型可分为三类,如图1所示。

图1 双平面滑体几何模型
由图1可得主动块l1和被动块l2的底滑面长度为:
式中:α1和α2分别为层理和缓倾节理的倾角,°;d为滑体厚度,d=nt1(t1为层理厚度),m;h为坡高,m。
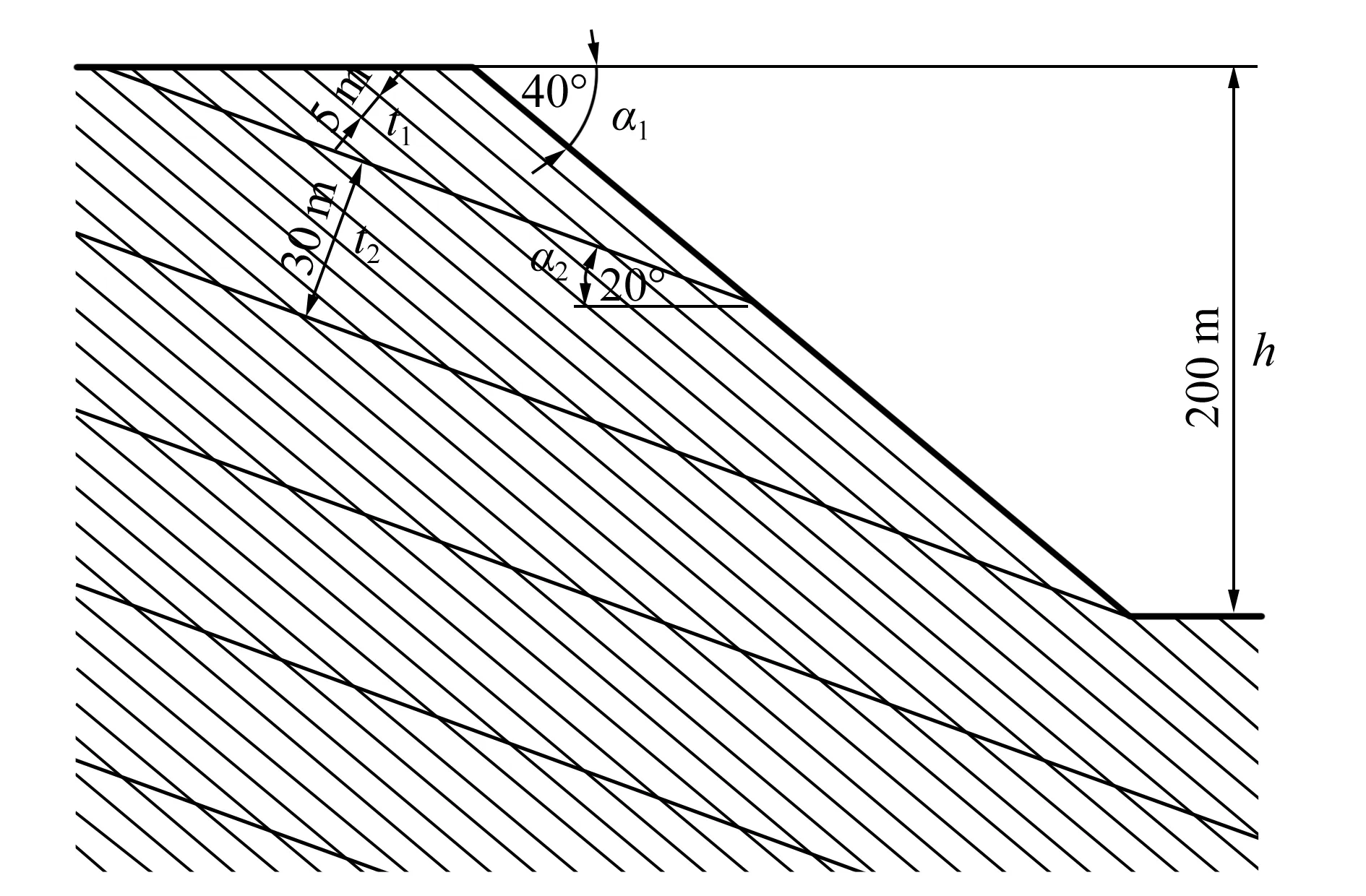
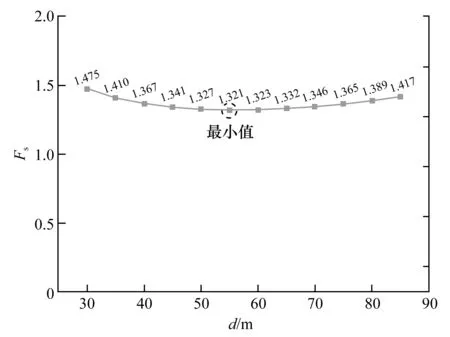
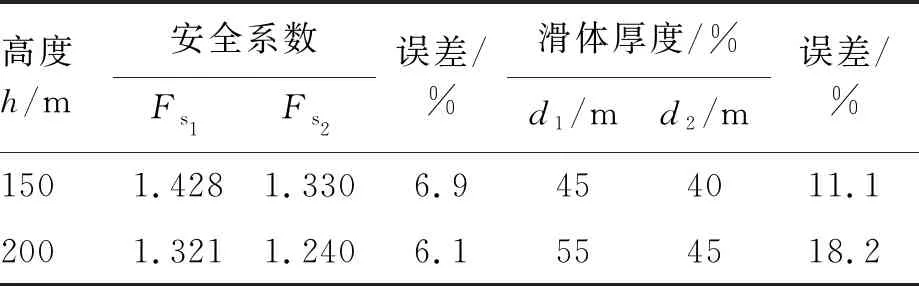
1)当l2cosα2 (3) (4) 2)当l2cosα2=hcotα1,几何模型为类型Ⅱ,主动块l1和被动块l2的重力为: 3)当l2cosα2>hcotα1,几何模型为类型Ⅲ,主动块l1和被动块l2的重力为: 从图1中可以看出,三类双平面滑体几何模型中主动块和被动块的力学作用机理相同,根据两者的受力特征建立了双平面滑体力学模型,如图2所示。 假设:1)主动块和被动块之间的相互作用力沿层理方向;2)主动块和被动块的底滑面满足莫尔-库仑强度准则,两者安全系数相等,均等于边坡安全系数。 由图2(a)中主动块的受力可得力平衡方程如下: 图2 双平面滑体力学模型 W1sinα1=S1+T (9) W1cosα1=N1 (10) 式中:S1和N1分别为层理上的切向力和法向力,N;T为主动块和被动块之间的作用力,N。 由图2(b)中被动块的受力可得力平衡方程如下: W2sinα2+Tcos(α1-α2)=S2 (11) W2cosα2+Tsin(α1-α2)=N2 (12) 式中:S2和N2分别为缓倾节理上的切向力和法向力,N。 由假设(2)可得: S1=(N1tanφ1+c1l1)/Fs (13) S2=(N2tanφ2+c2l2)/Fs。 (14) 联立式(9)~式(14),可得只含安全系数Fs的方程,如式(15)所示。整理式(15),可得含安全系数Fs的一元二次方程标准形式,如式(16)所示。 (15) (16) 其中: 采用一元二次方程求根公式即可求得Fs的值,将两个值分别代入式(9),舍掉使T为负值的Fs值,可得最终Fs的公式: (17) 对于给定几何参数和力学参数的顺层高边坡,可通过式(17)搜索顺层高边坡双平面滑动的潜在滑动面。具体方法为:取一定范围的滑体厚度d=nt1,分别计算不同d对应的Fs,其中最小Fs对应的d即为双平面滑动的潜在滑动面位置。 本节采用离散元分析程序Universal Distinct Element Code(UDEC)对一个典型的顺层高边坡进行双平面滑动机理及边坡稳定性分析,验证所提分析方法的合理正确性。 边坡高度通常指坡脚到第一个坡肩(或分水岭)的垂直高度[2]。高边坡的定义在不同领域和不同工业部门不尽相同,其中水利水电领域的高边坡定义高度最高,称天然边坡大于200 m或人工边坡大于100 m的边坡为高边坡。 顺层边坡的层理倾角一般在30°~60°之间[8-10,13-15],坡面在河流下切或人工开挖作用下往往沿层理面演化,形成了坡面近似和层理面产状近似一致的边坡。因此本文采用一个顺层高边坡概化模型进行探讨分析,模型如图3所示,边坡高度200 m,层理和缓倾节理倾角分别为40°和20°。坡内层理一般比缓倾节理发育,为计算方便,将两者间距都等效放大,层理和缓倾节理间距分别取为5 m和30 m。建立了离散元数值模型(UDEC模型),如图4所示。 图3 顺层高边坡地质几何模型 图4 顺层高边坡数值模型 在UDEC模型中,采用常用的边坡模型边界约束条件[19-20],即模型底边界固定X和Y方向速度,侧边界固定X方向速度。岩块采用莫尔-库仑本构模型,结构面采用库仑滑移模型。 边坡模型中岩体基本质量级别为Ⅲ~Ⅳ级,节理类别为2级,计算参数依据工程岩体分级标准(GB/T 50218—2014)[21]进行取值。具体基本计算参数见表1~表2。 表1 岩块计算参数 表2 节理计算参数 离散元数值计算中采用强度折减技术[22-23],同时折减岩块和节理的强度参数,折减系数为1.240时边坡临界破坏,所得计算结果如图5所示。 从图5中位移间断面特征可以看出,滑体呈明显的双平面滑动特征,上部滑体沿层理向下滑动,下部滑体沿缓倾节理向外滑出。 图5 位移分布图 双平面滑体的底滑面主要由层理和缓倾节理组成。上部滑体可称为主动块,下部滑体称为被动块[14-15,17-18],被动块在主动块的挤压推力作用下,层理和缓倾节理相互贯通,形成双平面滑动面,边坡发生双平面滑动破坏。 对概化案例边坡进行滑动面搜索,结果如图6所示。可以看出,边坡安全系数随滑体厚度增加呈先减小后增加的特征,存在一个最小安全系数,这个安全系数对应的滑体厚度即为边坡潜在滑动面位置。 图6 双平面潜在滑动面位置分析 从图6中可以看出案例边坡采用本文所提理论分析方法计算可得边坡安全系数(Fs1)为1.321,对应滑体厚度(d1)为55 m。采用UDEC强度折减法计算边坡安全系数(Fs2)为1.240,滑体厚度(d2)为45 m。结果见表3,两种方法计算所得安全系数误差为6.1%,结果近似一致;滑体厚度误差为18.2%,结果可被工程实践接受,该误差可以通过采用更精确的t1值分析得以降低。 此外,本节新增了一个150 m高度的顺层高边坡模型辅以验证分析方法的准确性,结果如表3所示。两种方法计算所得该边坡的安全系数误差为6.9%,滑体厚度误差为11.1%。因此本文所提顺层高边坡双平面滑动分析方法具有合理性和正确性。 表3 边坡安全系数和滑体厚度对比分析 本文基于顺层高边坡双平面滑动机理和极限平衡原理建立了双平面力学模型并提出了边坡稳定性分析方法,得到了主要结论如下: 1)顺层高边坡双平面滑体可分为上部主动块和坡脚被动块,在主动块对被动块的挤压推力作用下,层理和缓倾节理相互贯通,形成双平面滑动面,发生双平面滑动破坏。 2)边坡安全系数随滑体厚度增加呈先减小后增加的特征,存在一个最小安全系数对应的最危险滑动面位置。 3)本文所提分析方法与数值模拟强度折减法所得边坡安全系数和滑体厚度近似一致,可以准确便捷地用于边坡稳定性分析。2 稳定性分析方法
2.1 力学模型
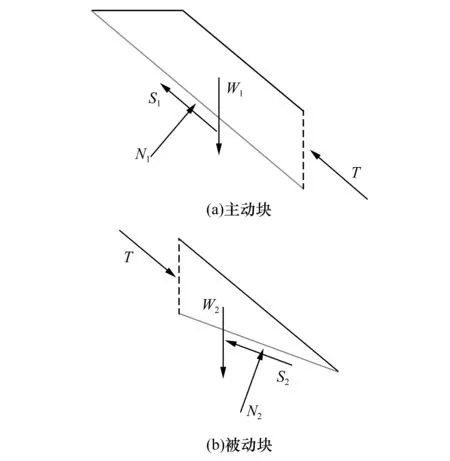
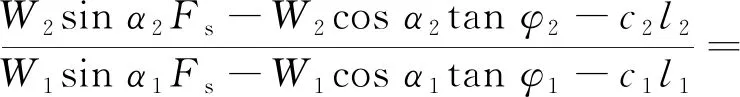
2.2 滑动面搜索方法
3 离散元数值模拟
3.1 计算模型及参数


3.2 双平面滑动破坏

3.3 对比分析
4 结 论

