二面体群D4pq的连通3度Cayley图的正规性

池建成

(安徽三联学院 基础部,安徽 合肥 230601)

Cayley图的正规性问题[1]一直是群与图的热点问题,取得的成果也颇为丰硕。文献[2]确定了除两类特殊群外,其余有限群皆有正规Cayley图。文献[3-4]解决了2p阶、pq阶Cayley图的正规性问题。文献[5-8]证明了除少数外,有限非交换单群的连通3度Cayley图皆是正规的。文献[9]给出了32p阶二面体群的3度Cayley图的分类。本文主要对4pq阶二面体群的连通3度Cayley图的正规性进行了分类,给出了除同构类S～{a,ab,apqb}不正规外,其余Cayley图皆是正规的结论,从而将二面体群阶的素因子个数推广到三个的情形。

1 预备知识

对于图X,本文用V(X),E(X)分别表示其顶点集与边集。若图自同构Aut(X)在V(X)上作用传递,则图X称为点传递。

设G为有限群,S为G的不含单位元的子集,定义群G关于S的Cayley图X如下:顶点集V(X)=G,边集E(X)={(g,sg)|g∈G,s∈S},记为X=Cay(G,S)。

由上述定义知:若S自逆,即S-1=S,则图X为无向图;若S为G的生成子集,即G=,则图X为连通图。图X的右正则表示R(G)包含在图自同构Aut(X)中,故而图X是点传递图。当R(G)◁Aut(X)时,称X=Cay(G,S)为正规Cayley图。

文中所涉及的图皆为无向、连通图,Xi(v)表示顶点v的i(i=1,2,3…)步邻域点集。

2 主要引理

引理1[1]X=Cay(G,S)为正规Cayley图⟺Aut(X)=R(G)·Aut(G,S)⟺Aut(X)关于单位元1的点稳定子群A1≤Aut(G)。

引理2[9]设Aut(X)关于1的点稳定子群是A1,X=Cay(G,S)非弧传递,若A1作用忠实且|A1|≤2,则X为正规Cayley图。

引理3[2]设X=Cay(G,S)为连通Cayley图,则X正规,若以下两个条件成立:

1)∀φ∈A1,若φ|X1(1)=1|X1(1),则φ|X2(1)=1|X2(1);

2)∀φ∈A1,∃α∈Aut(G),使得φ|S=α|S。

由文献[8]定理1易得引理4。

引理4设2n阶二面体群G=〈a,b|an=1,b2=1,b-1ab=a-1〉,X=Cay(G,S),其中S={aib,ajb,akb},i,j,k∈Zn,若n≥10且为偶数,则X=Cay(G,S)非弧传递。

引理5设2n阶二面体群G=〈a,b|an=1,b2=1,b-1ab=a-1〉,则群自同构Aut(G)中的任一元素σ满足σ:{a→ai

b→ajb,(i,n)=1。

引理6设二面体群G=〈a,b|a2pq=1,b2=1,b-1ab=a-1〉,其中p,q为互异的奇素数,S为群G的不含单位元的三元生成子集,且S-1=S,则在Aut(G)作用下,S同构于下列几种类型:

1)S1={a,a-1,b}

2)S2={apq,aib,b},其中i=1,2

3)S3={aib,ab,b},其中i≠0,1(mod2pq)

4)S4={aib,ajb,b},其中gcd(i,j)=1,gcd(m,2pq)∈{2,p,q,2p,2q,pq},m=i,j

证明因为S是群G不含单位元的三元生成子集,且S-1=S,所以,S中必然存在2阶元aib,同构意义下,可设其为b。

情形1S中仅有一个2阶元b,另外两个非2阶元,则这两个非2阶元互逆,从而这两个元素的同阶,且都是2pq阶元,在同构的意义下,可设为{a,a-1,b},即为S1。

情形2S中三个皆为2阶元,且2阶元apq包含其中,可设其为{apq,aib,b}。考虑到aib·b=ai,所以〈apq,ai〉=〈a〉,即〈pq,i〉=2pq,则i=2,或者i与2pq互素,同构的意义下,可设i=1,从而S={apq,aib,b},其中i=1,2,与S2相同。

情形3S中三个皆为2阶元,除b外,另两个2阶元形式为aib,ajb。由于aib·b=ai,ajb·b=aj,从而〈ai,aj〉=〈a〉,即〈i,j〉=2pq,所以即gcd(i,j,2pq)=1。若i,j有一个和2pq互素,同构意义下,可设j为1,即S={aib,ab,b},其中i≠0,1(mod2pq),与S3相同。若i,j都不和2pq互素,则i,j互素,从而S={aib,ajb,b},其中gcd(i,j)=1,gcd(m,2pq)∈{2,p,q,2p,2q,pq},m=i,j,与S4相同。

3 主要结论

定理1设二面体群D4pq=〈a,b|a2pq=1,b2=1,ab=a-1〉,其中p,q为互不相同的奇素数,S1={a,a-1,b},则X=Cay(G,S1)皆为正规的。

证明首先,∀φ∈A1,若φ固定了X1(1)={a,a-1,b}中的每个点,过点1,a,b的最小的圈仅有1个4圈{1,b,a-1b,a},过点1,a-1,b的最小的圈仅有1个4圈{1,b,ab,a},从而φ固定了点a-1b,ab。又过点a-1b,a的4圈仅有{a,a-1b,a-2b,a2},过点ab,a-1的4圈仅有{a-1,ab,a2b,a-2},从而又固定点a2,a-2,而X2(1)={a2,a-2b,ab,a-1b},所以φ|X2(1)=1|X2(1)。

其次,由上述可知,过1,a的4圈和过1,a-1的4圈都仅有一个,而过1,b的4圈有两个,所以∀φ∈A,都有{a,a-1}φ={a,a-1},取α:a→a-1,b→b,则α∈Aut(G),且{a,a-1}α={a,a-1},所以φ|S1=α|S1。由引理3知,X=Cay(G,S1)正规。

定理2设二面体群D4pq=〈a,b|a2pq=1,b2=1,ab=a-1〉,其中p,q为互不相同的奇素数,S2={apq,aib,b},i=1,2,则X=Cay(G,S2)皆为正规的。

证明与定理1的证明类似。

定理3设二面体群D4pq=〈a,b|a2pq=1,b2=1,ab=a-1〉,其中p,q为互不相同的奇素数,S3={aib,ab,b},i≠0,1,则除i=pq或i=pq+1非正规之外,X=Cay(G,S3)皆为正规的。

证明分下列几类情况证明。

情形1i=2时

过的4圈仅有{1,b,a,ab}和{1,a2b,a-1,ab},同定理1证法类似,此时可证明X=Cay(G,S3)正规。

情形2i=3时

经过点1,a3b的6圈共有3个,分别是{1,a3b,a-2,a2b,a-1,ab},{1,a3b,a-3,a4b,a-1,ab},经过点1,b的6圈共有4个,分别是{1,b,a3,a-2b,a2,ab},{1,b,a,a-1b,a2,ab},{1,b,a,a2b,a-2,a3b},{1,b,a,a2b,a-1,ab},经过点1,ab的6圈共有5个,分别是{1,ab,a2,a-2b,a3,b},{1,ab,a2,a-1b,a,b},{1,ab,a-1,a2b,a,b},{1,ab,a-1,a4b,a-3,a3b},{1,ab,a-1,a2b,a-2,a3b},任意φ∈A1,φ固定了X1(1)中的每个点,即φ=1,从而A1=1,得图X正规。

情形3当p,q中有一个是3,不妨设q=3,i=2p时

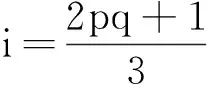
情形5i=pq,pq+1时

先证i=pq,取φ=(b,apqb)(a,apq+1)(a-1,apq-1)(a2b,apq+2b)。易检验φ∈A1,但φ∉Aut(G),由引理1知,此时图X非正规。当i=pq+1时,取

σ:{a→a-1

b→ab

知σ=Aut(G),而{b,ab,apq+1b}σ={ab,b,apqb},即i=pq+1时的图与i=pq时的图同构,图X也是非正规的。

情形6i非上述5种情形时

定理4设二面体群D4pq=〈a,b|a2pq=1,b2=1,ab=a-1〉,其中p,q为互不相同的奇素数,S4={aib,ajb,b},gcd(i,j)=1,gcd(m,2pq)∈{2,p,q,2p,2q,pq},m=i,j,则除i=2,j=pq非正规之外,X=Cay(G,S4)皆为正规的。

证明由组合关系,只需证下列几种情况:

1){a2b,apb,b},2){a2b,aqb,b}

3){apb,aqb,b},4){a2pb,aqb,b}

5){apb,a2qb,b},6){a2b,apqb,b}

情形1S4={a2b,apb,b}

情形2,3,4,5

与情形1证明类似,皆正规。

情形6取S4={a2b,apqb,b}

σ:{a→apq+2

b→apqb

知σ∈Aut(G),而{b,ab,apqb}σ={apqb,a2b,b},而由定理3知,当S={b,ab,apqb}时,图X非正规,从而当S4={a2b,apqb,b}时,图X也是非正规的,两图在同构意义下,是相同的。