粒计算的覆盖模型

王国朋,王永昭

(1.南京工程学院 数理学院,江苏 南京 211167;2.安阳师范学院 数学与统计学院,河南 安阳 455000)

粒计算最早由Zadeh于1979年提出[1],随后Pawlak与Hobbs也对这一问题进行了研究[2-3]。粒计算主要包含了信息的粒化和基于粒化信息的计算两个问题。粒化即基于相似关系、邻近关系或不分明关系等将问题空间进行划分得到粒层。粒计算则是基于划分得到的粒层求解问题,包含了不同粒层间信息的交互,以及相同粒层内部的运算等问题。1998年,Lin首次提出了邻域系统,讨论了关系数据库与领域系统的关系[4]。2004年,Yao在文献[4]的基础上对粒计算进行了进一步的研究,给出了一种基于划分的粒计算模型[5]。值得注意的是,文献[5]中的粒计算模型是基于等价关系给出来的。随后,Ma等将这一模型进行推广,仅保留等价关系中的自反性,得到了一类基于集合论覆盖原理的粒计算模型[6-7]。Sha等对粒计算模型做了进一步推广,得到了基于覆盖的近似空间上的粒计算模型,并详细研究了其性质[8-12]。

文章在文献[9]的基础上,进一步研究论域和粒化论域上由Zoom-in算子与Zoom-out算子复合得到的近似算子的性质,并讨论了所得近似算子与拓扑空间及Galois联络之间的关系。

1 预备知识

文献[9]给出了一种基于覆盖的粒计算模型,该模型放宽了文献[8]中的Zoom-in算子,从而得到了一种新的在不同粒层上粒子之间转换的模型。

定义1[9]设U为一个非空论域,C为U上的一个有限覆盖,若一元算子μ:2C→2U满足

∀X∈2C,μ(X)=∪{K|K∈X}

(1)

则称μ为一个Zoom-in算子。

该算子有如下性质:

1)μ(∅)=∅,μ(2C)=2U

2)X⊆Y⟹μ(X)⊆μ(Y)

3)μ(X∪Y)=μ(X)∪μ(Y)

4)μ(X)C⊆μ(XC)

(2)

2 主要结果

2.1 2U上的近似算子

文献[9]通过将Zoom-in算子与Zoom-out算子进行复合得到了论域空间上的一对近似算子,并证明了其就是基于覆盖的第二型上、下近似算子。下面将继续讨论其性质及其与拓扑空间和Galois联络之间的联系。

定义3[9]设U为一个非空论域,C为U上的一个有限覆盖,∀A⊆U,有

由Zoom-in算子与Zoom-out算子性质不难验证以下结论。

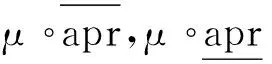
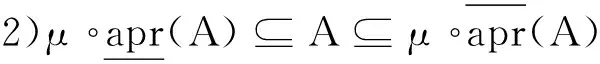
众所周知,拓扑空间与基于覆盖的粗糙集之间存在着一定的联系。由此不难想象,基于覆盖的粒计算模型也与拓扑空间之间存在着一定的联系。在讨论这一内在联系之前,先来看一元覆盖的拓扑刻画。

若B⊆P(X),∪B=X,且对任意的B1,B2∈B,∀x∈B1∩B2,存在B3∈B使得x∈B3⊆B1∩B2,称B是集合X上的拓扑J的一个基。

定理1设C为非空集U的一个覆盖,则C是一元覆盖当且仅当C为U上某个拓扑的基。

证明设C是一元覆盖,∀K1,K2∈C,x∈K1∩K2,则

x∈K1∩K2=∪y∈K1∩K2Md(y)

所以,∃y∈K1∩K2使得x∈Md(y)⊆K1∩K2,故C为U上某个拓扑的基。

反过来,设C为U上某个拓扑的基,假设存在x∈U使得Md(x)中至少有两个元K1,K2,显然x∈K1∩K2,所以应该存在K∈C使得x∈K⊆K1∩K2,这与K1,K2∈Md(x)矛盾,所以C是一元覆盖。

定义4设U为一个非空论域,称映射i:2U→2U为U上的一个拓扑的内部算子,若其满足:

1)i(U)=U, 2)i(A∩B)=i(A)∩i(B),

3)i(i(A))=i(A),4)i(A)⊆A

对偶地我们可以定义拓扑的闭包算子。

若一个算子满足定义4中的1)、2)、4),则称为一个内部算子;若该算子同时满足3)则称为一个拓扑内部算子。

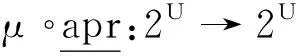
定义5设U为一个非空集合,U上的一个Galois连接为满足如下条件的映射对(f,g),f,g:2U→2U:

1)A1⊆A2⟹f(A1)⊆f(A2),g(A1)⊆g(A2)

2)f(g(A))⊆A,g(f(A))⊇A

由定义5可得如下结论:

证明必要性: 要证明C是U上的一个划分,只需证明:

∀Xi,Xj∈C,Xi∩Xj≠∅⟹Xi=Xj

=∪{X|X∩Xk≠∅}

因为x∈Xk且x∈Xi∩Xj,所以

从而Xi=Xj=Xk。

2.2 2C上的近似算子

定义6设U为一个非空论域,C为U上的一个有限覆盖,∀X⊆2C有

事实上,由Zoom-in和Zoom-out的定义可知, ∀X⊆2C有

={S∈C|∃Ki∈X,S∩Ki≠∅}

={S∈C|S⊆∪Ki,Ki∈X}

同样,由Zoom-in算子与Zoom-out算子性质不难证得以下结论成立。

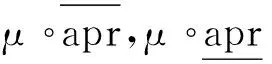
4)∀X,Y∈2C,

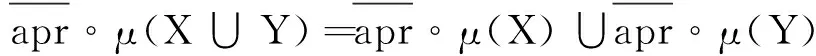
证明易证得1)～3)成立。

4) ∀X,Y∈2C

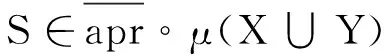
⟺∃Ki∈X∪Y,S∩Ki≠∅

⟺∃Ki∈X,S∩Ki≠∅

或∃Ki∈Y,S∩Ki≠∅

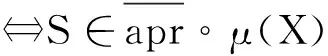
5) ∀X∈2C

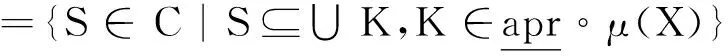
={S∈C|S⊆∪K,K⊆∪M,M∈X}

={S∈C|S⊆∪M,M∈X}

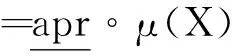
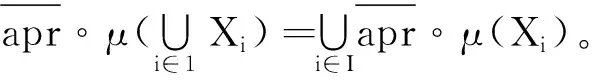
⟺∃K∈Xi,S∩K≠∅

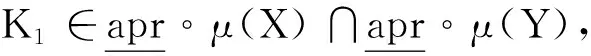
定义7设U为一个非空论域,称映射i:2C→2C为2C上的一个预拓扑内部算子,若其满足:

1)i(2C)=2C

2)X⊆Y⟹i(X)⊆i(Y)

3)i(i(X))=i(X)

由推论1可以得出以下结论:

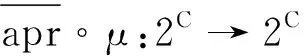
定义8设U为一个非空论域,称映射cl:2C→2C为2C上的一个预拓扑闭包算子,若其满足:

1)cl(∅)=∅

2)cl(X∪Y)=cl(X)∪cl(Y)

3)X⊆cl(X)

由此,不难得出以下结论:

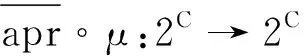
证明必要性:要证明C是U上的一个划分,只需证明:

∀Xi,Xj∈C,Xi∩Xj≠∅⟹Xi=Xj

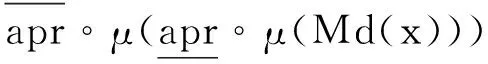
={S∈C|Ki⊆∪Mi,Mi∈Md(x),S∩Ki≠∅}

={S∈C|∃Mi∈Md(x),S∩Mi≠∅}

⊆Md(x)

因为Md(x)={Xk}且x∈Xi∩Xj,所以

⊆Md(x)={Xk}

从而Xi=Xj=Xk。

3 结论

在问题空间及粒化了的问题空间上,基于文献[8-9]研究了由Zoom-in算子和Zoom-out算子复合得到的广义粗糙近似算子的性质,并讨论了其与拓扑内部算子、闭包算子及Galois联络之间的关系。