单轴虚拟振动试验技术研究

赵艳涛，陈耀，李健，贾俊杰

（航天科工防御技术研究试验中心，北京 100854）

在开展实物振动试验时，会有振动台推力不够、关心部位不易粘贴传感器而不能获得其振动情况、实物试验周期太长、实物试验验证滞后等局限。虚拟振动试验成本低，不受客观条件限制，获取数据全面，可以加快设计更新迭代、缩短设计周期、大型试验前优化试验方案等优点。虚拟试验可以弥补实物试验的种种不足而越来越受到重视。国外对虚拟振动的研究已经取得了不少成果，并在工程实际中开展应用。国内已经有多家单位开展了相关的研究，主要有有限元模型结合开环振动分析、建立振动台有限元模型结合闭环振动控制等，但应用还有频率范围、试验类别等诸多的限制。本文着眼于以有限元构建振动台平台的基础上，结合随机振动控制算法，搭建闭环随机振动虚拟试验系统，可以将经校准后的不同产品模型“安装”在该系统中，开展随机振动虚拟试验，具有一定的通用性。

1 闭环随机振动虚拟系统搭建

本文构建了闭环随机振动虚拟试验系统，虚拟振动整体系统如图1 所示。振动台系统简化为振动控制系统和振动台机械模型2 部分，其中功放系统和滤波放大电路可以分别测量各自的频响函数[1]，再和振动台机械部分的频响函数联合起来，构成系统的频响函数，控制仪根据系统的频响函数来进行振动控制。由PATRAN 建立振动台有限元模型，并生成系统频响函数文件，由MATLAB 读取后进行整个控制计算。

图1 虚拟振动整体系统Fig.1 Diagram of overall virtual vibration system

1.1 控制仪模型[2-4]

随机振动试验的控制过程如图2 所示。控制仪首先根据参考谱生成驱动谱，由驱动谱生成频谱，经逆傅里叶变换后，得到伪随机信号，并转化为真随机信号来驱动振动台。将传感器测量结果和参考谱进行比较后，生成下一次的驱动谱。

图2 随机振动虚拟试验控制过程Fig.2 Control process of virtual random vibration test

1）频响函数的估计[5]。频响函数可通过式（1）得到[6]：

式中：PSDCD为驱动信号和响应信号的互谱，g2/Hz；PSDDD为驱动信号自谱，g2/Hz；H为系统的频响函数。

2）随机振动试验控制中，由系统频响函数和参考谱可得到如下驱动谱：

式中：PSDR为参考谱，g2/Hz；PSDD为驱动谱，g2/Hz。

由参考谱和当前的驱动谱得到下一次的驱动谱，如式（3）所示[7]。

式中：(PSDD)i为当前驱动谱；(PSDD)i+1为下一次的驱动谱；(PSDC)i为当前控制谱。

这是随机振动的驱动谱（频域）均衡迭代的核心算法，当然也还有其他的随机振动控制算法，驱动谱转化为时域驱动信号来驱动振动台。

3）驱动谱（频域）转换为时域的驱动信号。由驱动谱可以得到驱动信号的幅值，单独幅值信息不能够转换得到时域信号，因此进行相位随机化后，将驱动信号的幅值再附加随机的相位信息后，进行逆傅里叶变换，可以得到时域的伪随机信号。伪随机信号还不可以直接作为时域的驱动信号，需进行时域随机化处理。对相位随机化后的伪随机信号经过延迟和反向后，得到多组时域信号，然后进行加窗叠加，就得到了可用于时域驱动信号的真随机信号[8-9]。

时域驱动信号经过功放系统放大后，驱动振动台中的运动部件运动，传感器将加速度信号通过滤波放大电路传递给控制仪。控制仪根据当前传感器测试得到的当前控制谱，结合参考谱和当前驱动谱，按照式（3）做迭代计算后，输出下一次的驱动谱。

1.2 振动台机械模型建模

1.2.1 振动台几何模型

振动台主要包括动圈和台体，动圈通过上悬挂弹簧和下导向轴承固定在台体上，台体通过空气弹簧固定在底座上，如图3 和图4 所示。动圈是主要活动部件，产品通过夹具安装在动圈上，动圈带动产品运动。动圈主要包括骨架和线圈，线圈作为固定连接在动圈骨架上。通过建立有限元模型，并附加边界条件来模拟振动台。

图3 振动台整体模型Fig.3 Overall model of vibration table

图4 动圈模型Fig.4 Moving coil model

1.2.2 动圈的有限元模型

动圈是振动台的核心部件，采用有限元软件对动圈进行网格划分。划分网格时，既要保证网格精度，又要兼顾计算效率，对不规则部分采用四面体网格划分，对规则部分采用面单元进行网格划分，如图5 所示。

图5 动圈及台体的有限元模型Fig.5 Finite element model of moving coil (a) and platform (b)

动圈骨架和线圈之间连接的模态对应的特征频率都远在振动台的工作频率之外，对系统响应的影响比较小，将骨架与线圈间简化为刚性连接，将动圈作为一个刚性整体。骨架为各向同性材料的镁铝合金，线圈作为驱动力的来源，既要导电又要降温，其由铜导管绕制而成，铜导管本身导电，内部通过冷却水来降温，通过特种胶将铜导管粘接在一起，外部再通过钢片粘接固定。为了方便分析，将线圈材料简化为各向同性材料进行处理[10-12]。

在保证几何模型与实物相符的前提下，来调整密度和弹性模量这2 个材料参数[13]，使模态仿真结果与模态试验结果一致，即可认为此有限元模型可以用于虚拟振动。

1.2.3 动圈的边界条件

动圈上端四周有4 个间隔90°的悬挂弹簧将动圈悬挂在台体上，可以限制动圈的横向振动和扭转。另外，动圈中央竖直方向的刚性轴通过空气弹簧连接在台体上，上下悬挂系统都通过弹簧单元来简化，仅保留轴向平动自由度，保证动圈沿竖直方向运动。中心刚性轴对动圈的导向作用通过多点约束单元（MPC单元）的来进行模拟，并约束其他所有自由度，而只保留竖直方向运动[14-15]。

台体作为动圈的支撑系统，按照其几何模型进行网格划分。台体通过空气弹簧悬挂在底座上，如果工作频率比较高，可以忽略空气弹簧的影响；如果工作频率比较低，则需要考虑空气弹簧的影响，空气弹簧可采用弹簧单元来简化。

1.2.4 模态试验验证

分别对动圈、夹具、产品建立有限元模型，并结合模态试验进行有限元模型校准。模态试验中，分别对被试对象用橡皮绳悬挂后，采用锤击法开展模态试验，多次锤击获取有效数据后，通过PolyLSCF 法识别模态参数，再通过MAC 矩阵来验证获取的模态参数是否可信。在保证模态试验结果可信的基础上，修正有限元模型的过程如下：在几何模型与实物相符的前提下调整材料参数，在参考材料基本参数的基础上，首先微调密度来保证质量与实际质量一致[18]，再微调弹性模量，使模态仿真结果与模态试验结果比较接近，主要模态频率最大相对误差在5%以内，使得振动台各部分的材料参数能够反映真实的材料特性，可认为有限元模型是可信的[16]。夹具模态仿真和模态试验的主要模态频率比对见表1，振型如图6 所示。产品模态仿真和模态试验的主要模态频率比对见表2，振型如图7 所示。动圈模态仿真和模态试验的主要模态频率比对见表3，振型如图8 所示。

表1 夹具模态仿真和模态试验模态频率比较Tab.1 Comparison of modal frequencies of fixture modal simulation and modal test

图6 夹具各阶振型Fig.6 Various vibration modes of fixture: a) 1st order;b) 2ed order;c) 3rd order;d) 4th order;e) 5st order;f) 6th order;g) 7th order;h) 8th order

表2 产品模态仿真和模态试验模态频率比较Tab.2 Comparison of modal frequencies of product modal simulation and modal test

图7 产品各阶振型Fig.7 Various vibration modes of product: a) 1st order;b) 2ed order;c) 3rd order

表3 动圈模态仿真和模态试验模态频率比较Tab.3 Comparison of modal frequencies of moving coil modal simulation and modal test

图8 动圈各阶振型Fig.8 Various vibration modes of moving coil: a) 1st order(torsion);b) 2ed order (breathe);c) 3rd order (Telescoping)

实物试验中，夹具与产品、夹具与动圈通过螺栓连接。开展产品虚拟振动试验时，动圈与夹具、夹具与产品螺栓连接处，建模时通过刚性连接来代替螺纹连接。单元类型采用RBE2（刚体单元）[17]。将产品、夹具的有限元模型与振动台的动圈模型进行连接，构成振动台机械系统的有限元模型，结合随机振动控制仪模型，构建整个虚拟振动闭环控制系统，进行虚拟振动闭环控制，来确定振动试验控制方案、产品的振动量级等。

在进行模型修正时，首先根据模态试验结果，在修正密度使模型与实物质量相符后，再调整弹性模量，使虚拟试验和实物试验在模态频率和振型上一致，使模型的刚度矩阵、质量矩阵得到修正。其次，侧重对结构阻尼、结构件之间的连接关系、边界条件、弹性模量等参数进行反复修改，使测点的虚拟试验与实物试验结果一致。可参考文献[18]中的方法进行分区和参数修改，可以快速修正目标，满足工程需要，详细过程见该文献。

2 虚拟振动和实物试验结果的比对

目标谱为梯形谱，谱形如下，20～80 Hz：+3 dB/Oct；80～350 Hz：0.04g2/Hz；350～2 000 Hz：–3 dB/Oct。均方根值6.06g。夹具为正方形板状结构，产品通过夹具安装在振动台台面上。选取靠近夹具4 条边线的中点及中心点作为控制点（如图9 所示），采用多点平均值控制。

图9 振动控制点示意图Fig.9 Diagram of vibration control points

选取产品上测量点为1#（位于产品顶圈壁面，对应节点542200）、2#（位于产品中圈壁面，对应节点542883），如图10 所示。实物试验及虚拟试验结果比对分别如图11、图12 所示。

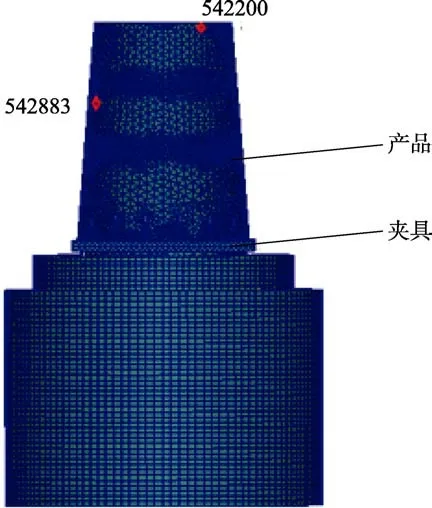
图10 振动系统有限元模型及测量点Fig.10 Finite element model and measuring points of vibration system

图11 1#实物与虚拟试验结果比对及仿真时域波形Fig.11 Comparison of 1# physical and virtual test results (a) and simulated time domain waveform (b)

图12 2#实物及虚拟试验结果比对及仿真时域波形Fig.12 Comparison of 2#(node542883) physical and virtual test results (a) and simulated time domain waveform (b)

从表4 可以看出，400 Hz 以前，虚拟试验和实物试验的均方根值误差明显小于全频段内的。另外，400 Hz 以内，1#的最大功率谱密度误差为0.034g2/Hz，2#的最大功率谱密度误差为0.038g2/Hz。在400Hz以上的高频段内，功率谱密度误差远远超过400 Hz前的低频段。

表4 不同频段实物试验和虚拟试验均方根值比较Tab.4 Comparison of root mean square values of physical test and virtual test in different frequency bands

通过比对实物试验和虚拟试验结果，由曲线的趋势可以明显看出，二者在400 Hz 之前的低频段，整体趋势一致性相对较好，在高频段的一致性相对较差。这和高频段模态比较复杂、随机振动在高频段难控制是一致的。在建模过程中，由于很多细节进行了简化处理，会影响到高频部分的仿真结果。另外，网格划分受到计算机计算能力的限制，不能划分足够小的尺寸，也会影响到虚拟试验高频部分结果。同时，高频段在实物试验时难免会出现一定程度的非线性，但仿真计算是基于线性假设，这就难以保持二者在高频段的一致[22]。

3 结语

结合有限元和闭环随机振动控制方法搭建的随机振动虚拟试验系统在400 Hz 前的低频段有相对较好的可信度，高频段的虚拟试验结果精度还有待提高。这种方法搭建的随机振动虚拟振动系统的虚拟振动是一个比较复杂的过程，涉及到许多的技术细节，以上只是初步的工作，想要虚拟振动试验系统通用性更强，得到更准确的结果，则需要进一步进行详细建模和修正。另外，本文只进行了虚拟振动的初步探索，后续可结合工程实践进一步完善和推广应用。

1）单轴虚拟振动是双台振动和多维振动的基础，在单轴虚拟振动的基础上开展双台虚拟振动和多维虚拟振动。

2）虚拟振动还有很多局限，实物振动试验中，装备在振动载荷下，其动力学特性普遍存在变化，频响函数是实时变化的，但目前基于有限元方法获取频响函数不能实时变化，虚拟振动试验还和实物振动试验有差异，虚拟振动试验不能替代实物振动试验。可开展基于数字孪生的虚拟振动试验技术研究，根据实测试验数据，对有限元模型进行实时修正。

3）基于有限元模型开展的虚拟振动在低频段相对准确，结合产品经历振动环境的频段，高频段可结合统计能量法开展相关的研究。