考虑墙背倾角的挡土墙地震主动土压力研究

周 勇, 都浩男, 王正振

(1. 兰州理工大学 甘肃省土木工程防灾减灾重点实验室, 甘肃 兰州 730050; 2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050; 3. 兰州理工大学 土木工程学院, 甘肃 兰州 730050)

挡土墙作为一种可以有效防止墙后土体变形的支挡结构,被广泛地应用在建筑工程、道路交通、水利等工程建设中.土压力是其主要的受力来源,但是通过对地震中挡土墙的破坏统计研究发现,地震的动力作用对挡土墙所受到的土压力影响十分显著[1],因此研究地震土压力具有十分重要的实际意义.与此同时,挡土墙实际工作状态下的土体位移并不能达到经典的朗肯土压力理论和库伦土压力理论所假设的极限土体位移[2].因此土压力计算应考虑墙体位移和变位模式的影响.

传统的Mononobe-Okabe理论以库伦土压力理论为基础,采用拟静力法把动力问题转化为静力问题.该理论有计算地震情况下的土压力简单方便等优点,但同时也存在着仅适用于无粘性土、只能计算极限状态下的地震土压力等缺陷.Ichihara[3]、Morrison[4]等研究表明,Mononobe-Okabe法计算得到的地震土压力合力和实验所得的结果较为吻合,但是地震土压力合力的作用点高度并不是固定的H/3处.

朱彦鹏等[5]研究了有限土体主动土压力计算方法;宋征等[6]在Mononobe-Okabe理论基础上基于应力状态推导了粘性土的地震主动土压力计算方法,但未考虑墙背倾角、位移等因素的影响;杨剑等[7]将地震力按最不利工况下的静力考虑,利用水平层分析法推导得出了地震加速度沿墙高均匀分布时不同挡土墙倾角,填土内摩擦角,墙背摩擦角下的地震被动土压力系数、被动土压力强度及被动土压力合力的计算公式,但未考虑填土表面的坡角和填土表面荷载的影响及主动土压力计算方法;陈奕柏等[8]采用斜向条分法给出了粘性挡土墙地震土压力的解析解,但其并未考虑位移及变位模式对土压力的影响;宋飞等[9]基于拟静力和曲面中间滑楔体的概念,给出了挡土墙平动模式下滑裂面为曲面时的被动地震土压力计算方法,但未考虑绕墙底转动等其他位移模式;黄睿[10]在Mononobe-Okabe理论的基础上,考虑了土拱效应、挡土墙位移和二维渗流作用等复杂因素影响,推导了地震土压力计算方法,但其仅考虑了挡土墙多种位移模式中的平动位移;王学民等[11]考虑土拱效应和黏聚力推导了倾斜挡墙非极限主动土压力;林宇亮等[12]采用水平层分析法推导了地震作用下粘性土的动土压力计算公式,并采用图解法得到了临界破裂角的显式解答,但没有考虑位移对土压力的影响;俞缙等[13]改进了挡土墙非线性土压力的计算方法;李刚[14]等分析了不同变位模式下挡土墙的动土压力计算方法,但其建立在土体达到极限状态的基础上,未给出“中间状态”动土压力计算公式,且其假设墙背竖直且土体为无粘性土.

在实际工程中,挡土墙位移模式除了平动之外还有绕墙趾转动等其他位移模式[15].目前对于倾斜挡土墙绕墙趾转动位移模式下的地震土压力研究较少.本文以墙背倾斜的重力式挡土墙为研究对象,考虑绕墙趾转动的位移模式和位移对摩擦角发挥的影响,利用水平层分析法建立了该位移模式下地震主动土压力分析模型,推导了挡土墙地震土压力分布、土压力合力及合力作用点的理论公式.利用文献[1]挡土墙试验模型进行了计算分析,并进行了数值模拟,分析了地震系数对主动土压力强度、最危险滑裂面倾角、合力作用点高度及地震主动侧土压力系数等因素的影响.

1 地震主动土压力计算模型

如图1所示,挡土墙垂直高度为H,墙顶的均布荷载为q,与竖直方向的倾角为α,土体破坏时将沿过墙趾点且与水平面夹角为θ的平面OB发生滑动,假定墙后土体为无粘性土.设填土内摩擦角为φ,墙后土体与挡土墙的摩擦角为δ,由于本文考虑墙体位移对地震土压力的影响,故φ、δ按式(1)计算[16-17]:

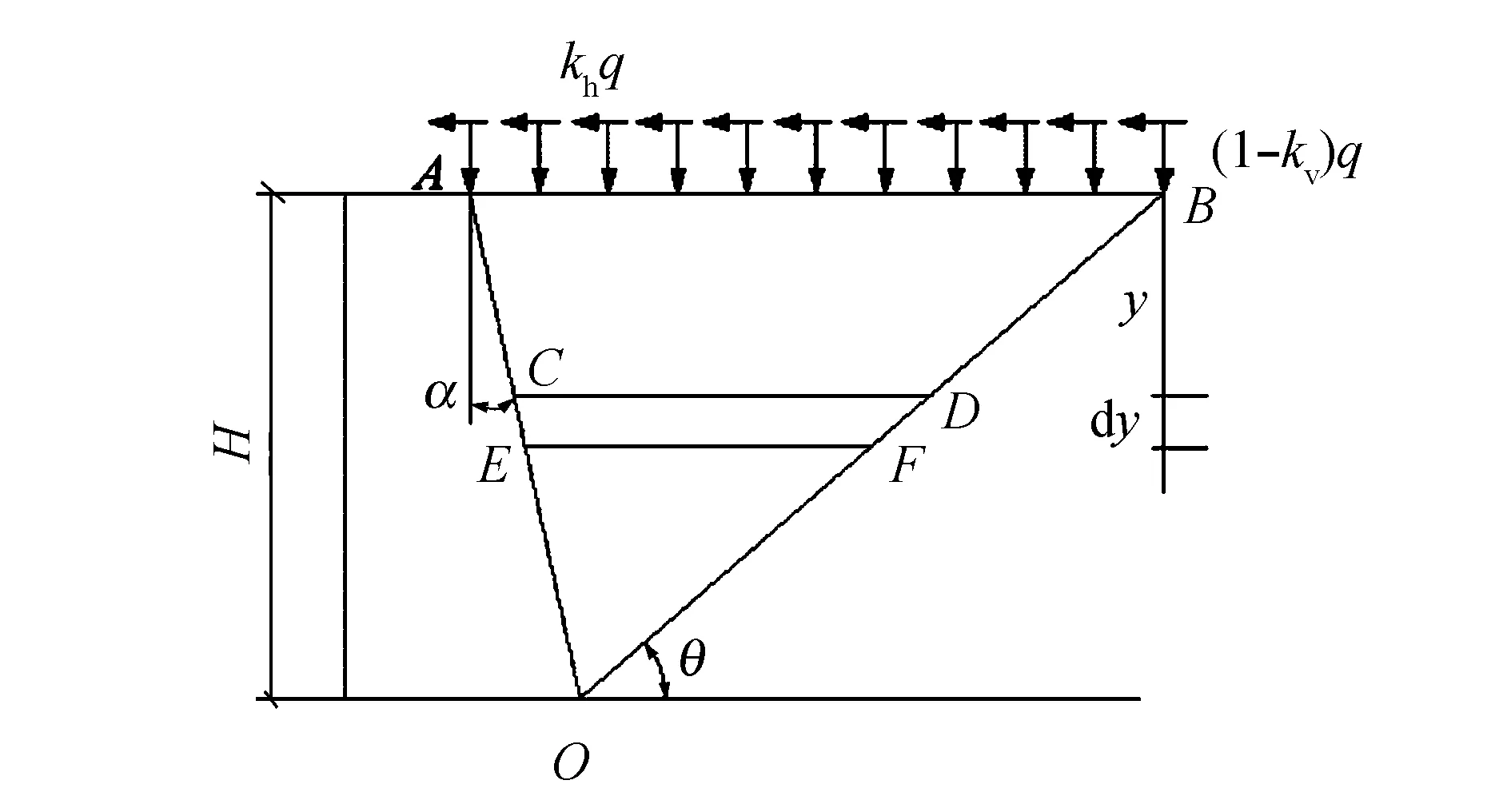
图1 挡土墙分析模型

(1)

式中:Kd=S(y)/Sa,Kd为土体位移对δ和φ的影响系数;S(y)为土体距墙顶y处的水平位移量;Sa为土体达到主动极限状态时的位移量,由挡墙绕墙底转动试验[13]取Sa为0.005H.φ0和δ0的取值参考文献[18].

如图2所示,从墙后土体y深度处取一厚度为dy的水平微元体,对微元体受力分析可得,微元体受到y顶面竖向压力py和水平剪切力pytanφ,底面竖向反力py+dpy和水平剪切力pytanφ+d(pytanφ),墙面作用有法向反力px和平行于墙面的墙土摩擦力pxtanδ,滑动面作用有土体反力R和摩擦力Rtanφ,竖直向下的微元体重力dw,水平地震力khdw和竖直地震力(1-kv)dw.由于地震加速度的大小和方向具有很大的随机性,本文考虑最不利工况下的地震力方向(即水平地震作用指向挡土墙方向,竖直地震作用竖直向下).

图2 水平微元体受力分析

2.1 土压力分布

由图2中几何关系可得

(2)

dw=γ(H-y)(tanα+cotθ)dy

(3)

对微元体进行受力分析,由作用于单元体上的水平方向力的平衡条件∑x=0得

(4)

联立式(2～4)并略去二阶微量得

(5)

由竖向力的平衡条件∑y=0可得

(6)

联立式(2,3,6)并略去二阶微量得

(7)

令px=kpy,式中k为填土侧向土压力系数,由式(5)可得

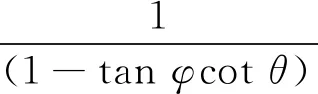
γkh(H-y)(tanα+cotθ)+

kpy(1-tanαtanδ)-

(8)

将式(8)代入式(7)化简得

(9)

式中:

求解式(8)可得地震主动土压力为

(10)

其中,C为积分常数,由边界条件确定,当y=0时,py=(1-kv)q,则

(11)

则联立式(10)和式(11)可得作用于挡土墙上的土压力为

(12)

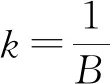
(13)

此时土压力为线性分布.

2.2 地震主动土压力合力

对式(11)沿墙的高度积分可得作用于挡土墙法向的地震土压力为

(14)

则此时地震主动土压力合力为

(15)

假设地震主动土压力系数为Ke,则Ke可以表达为

(16)

将式(14)进一步简化,所得地震主动土压力合力与Mononobe-Okabe公式是一致的[19].

2.3 地震主动土压力合力作用点

作用在挡土墙上的水平土压力对墙底取矩为

(17)

则挡土墙地震主动土压力合力作用点距墙趾的距离为

(18)

当地面荷载q=0时:

(19)

2.4 计算步骤

1) 根据不同的挡土墙位移量通过式(1)求得与位移量相对应的土体内摩擦角φ和墙土摩擦角δ,将其和墙背倾角、填土表面超载、土体物理力学参数等已知参数代入式(15).得到土压力合力Ea关于滑裂面倾角θ的函数表达式,根据库伦理论,令dEa/dθ=0,采用MATLAB解得最危险滑裂面倾角.

2) 将所有已知参数代入式(12)求解,得到沿墙高任一点的土压力强度.

3) 将已知参数及步骤一所求得θ值代回式(15)求解,得到土压力合力;代入式(18)求解,得到合力作用点高度;代入式(16)求解,得到地震主动侧土压力系数.

3 算例分析

挡土墙高H=8 m、土体内摩擦角φ=35°、墙背与填土摩擦角δ=2/3φ、土体重度γ=19.8 kN/m3、墙背倾角和墙后填土坡角α=β=0、填土表面均布超载q=0、土体粘聚力c=0、水平地震系数kh=0.2、竖向地震系数kv=0(汶川波)[1].

3.1 土压力的分布

图3为挡土墙绕墙趾转动时不同转角位移下沿墙高的地震土压力强度计算值曲线.从图中可以看出,当位移比S(y)/Sa=0时(静止土压力状态)土压力最大.随着位移的增大,土压力逐渐减小,当S(y)/Sa=1时(主动土压力状态)土压力最小,符合库伦土压力理论中静止土压力大于主动土压力的思想.分布曲线均呈现出沿墙高非线性分布的特点,随着深度增加,地震主动土压力强度逐渐增大,且增大幅度也随之增大,地震主动土压力最大值出现在墙体接近墙趾处.计算所得曲线形状与卢坤林等[20]所得绕墙底转动刚性挡土墙主动土压力曲线形状一致,为向下凹的递增曲线.

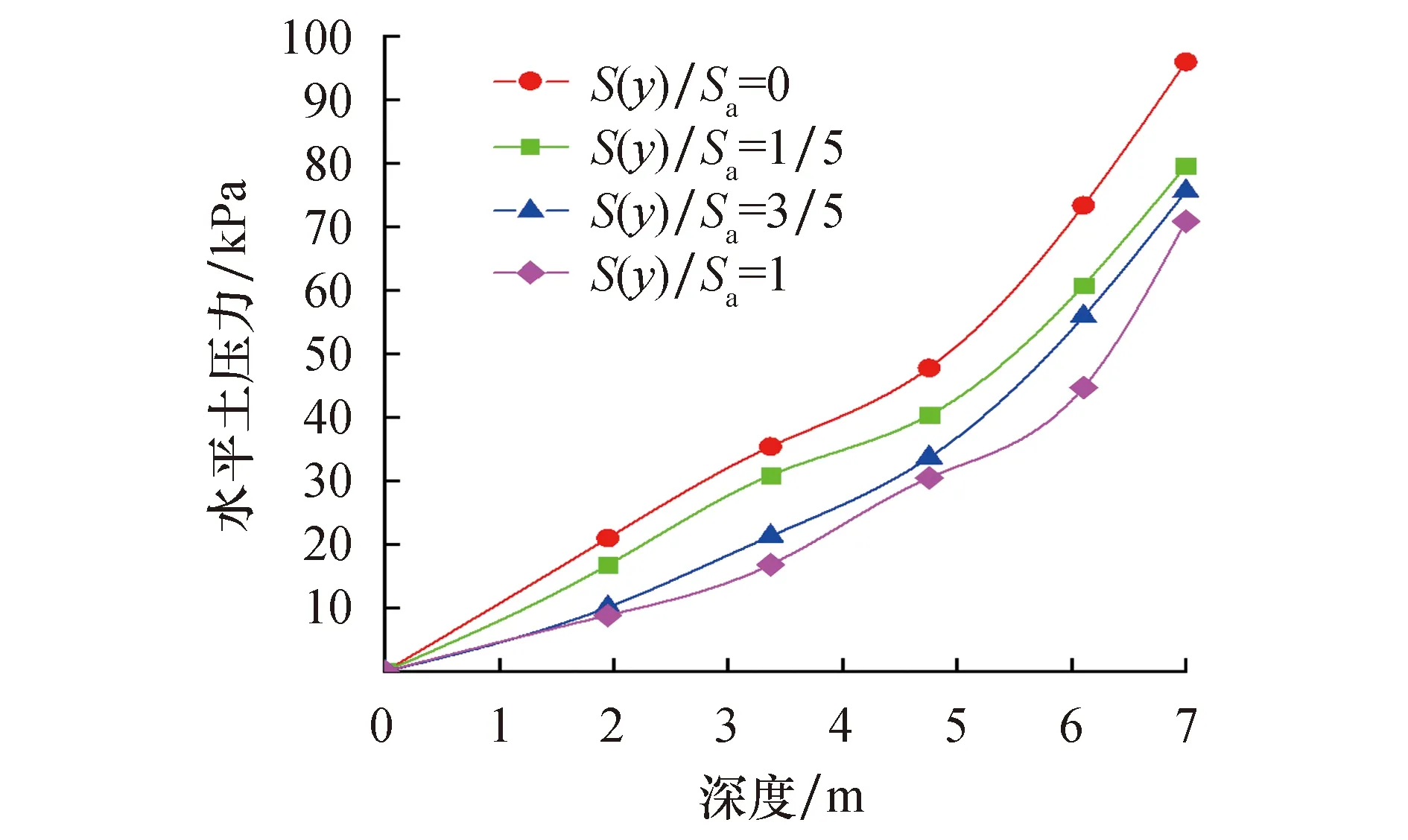
图3 土压力计算值随位移变化关系

图4为位移比为Smax/Sa=1/5时在不同水平地震系数下地震土压力强度沿墙高的分布图.当竖向地震系数kv不变时,随着水平地震系数kh增大,土压力强度也随之增大,且土压力增加幅度也逐渐增大.从土压力计算数值分布曲线中可以看出土压力在挡土墙下部增幅大于上部,即表现为随着地震系数的增大,土压力合力作用点下移.

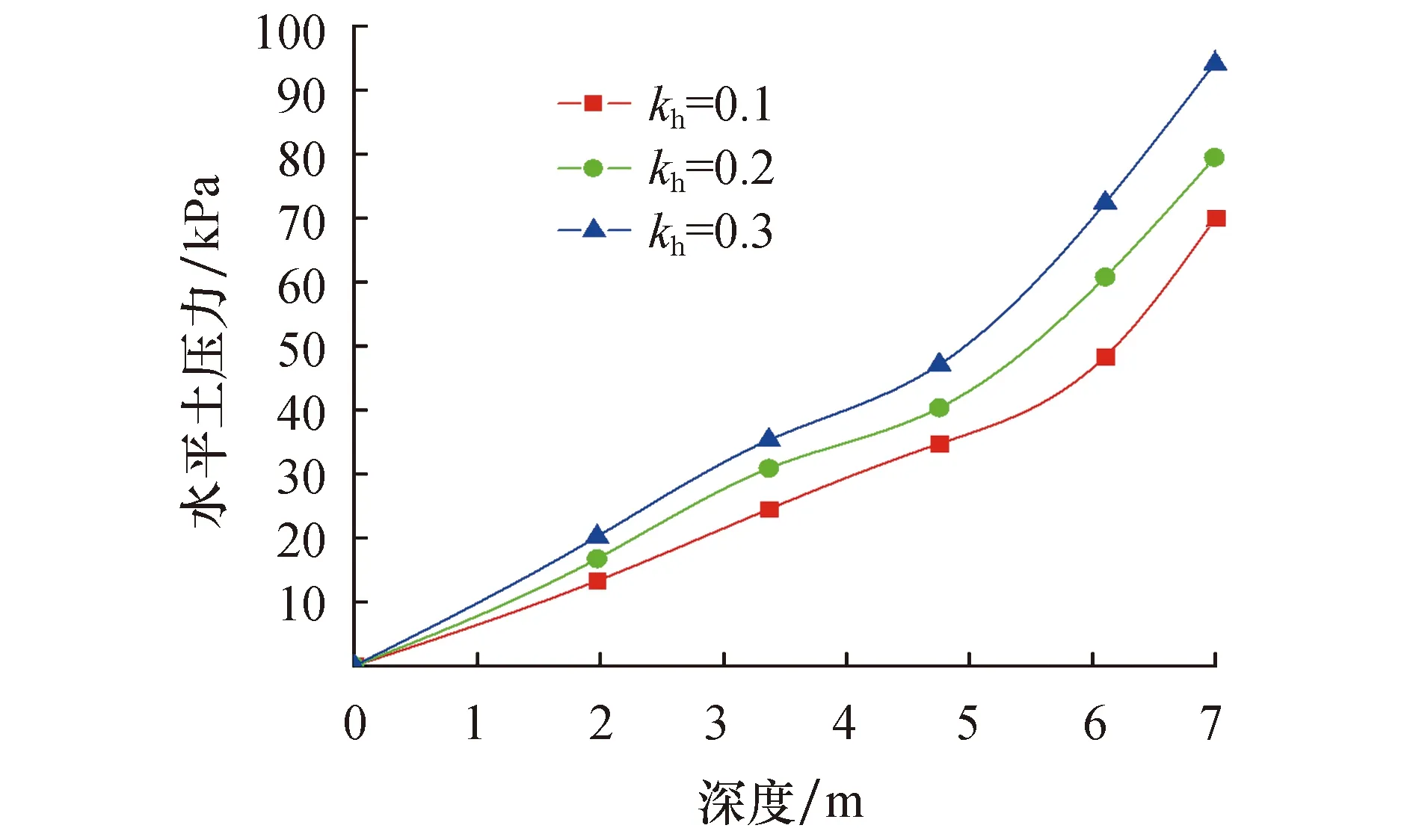
图4 土压力计算值随地震系数变化曲线

3.2 滑裂面倾角

根据库伦理论的思想,当挡土墙绕墙趾向外转动时,最危险滑动面上的地震主动土压力是最小的,所以对于式(15),令dEa/dθ=0即可求得最危险滑裂面倾角.图5为取δ=φ/3时滑裂面倾角θ随地震系数kv、kh的变化关系.由图5可以看出,当水平地震系数kh=0时,无论竖向地震系数kv值如何变化,滑裂面倾角θ的值大小基本保持不变.由此可以看出在水平地震系数为0时竖向地震系数对滑裂面倾角的影响很小,可以忽略不计.当kv、kh均不为0时,θ随水平地震系数kh的增大而减小,随竖向地震系数kv的增大而减小.

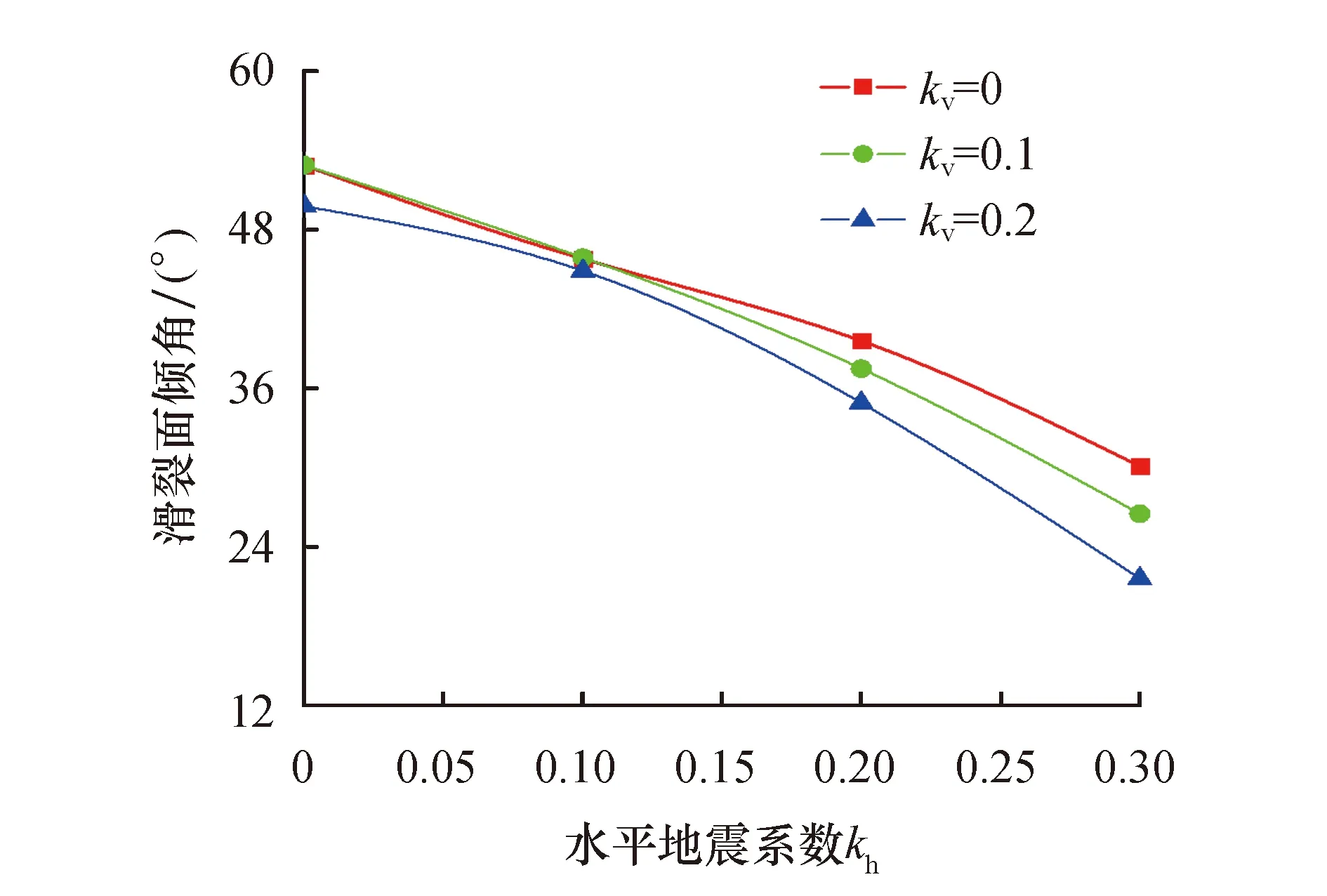
图5 滑裂面倾角随kv、kh的变化曲线

3.3 合力作用点

地震主动土压力合力作用点高度可由式(18)求得,当填土表面荷载q=0时,合力作用点高度由式(19)求得.图6为不同地震系数下的合力作用点高度.从图中可以看出,当kh=0时,合力作用点高度基本保持不变,为0.33H.kv保持不变时,合力作用点随kh的增大而减小,kh保持不变时,合力作用点高度随kv的增大而减小,且变化幅度随地震系数的增大而增大.当α=0时,与黄睿[7]计算所得结果变化趋势相一致,即当墙体位移量不变时,绕墙底转动位移模式下的地震主动土压力合力作用点高度随地震系数的增大而减小.

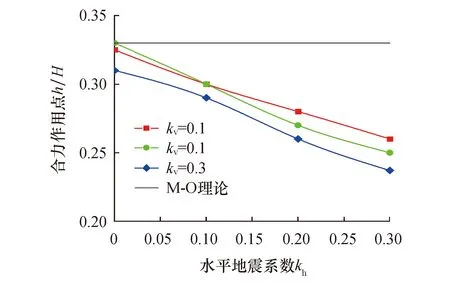
图6 合力作用点随kv、kh的变化曲线

3.4 主动侧土压力系数

图7为地震主动侧土压力系数随挡土墙的墙背倾角和地震系数的变化关系.从图中可以看出,当挡土墙的墙背倾角从-30°逐渐变化到30°时,挡土墙地震主动测土压力系数随之增大,且随着角度增大,主动侧土压力系数增大的幅度也随之增大.当挡土墙的墙背倾角保持不变时,随着地震系数的增大,挡土墙侧主动土压力系数增大.以kv=0.1、kh=0.2对应曲线为例,当墙背倾角α=-30°时,主动侧土压力系数ke为0.32;当α=0时,土压力系数ke为0.508;当α=30°时,土压力系数ke为0.87.由此可以看出,挡土墙设计为俯斜时所受法向地震主动土压力比仰斜时更小.

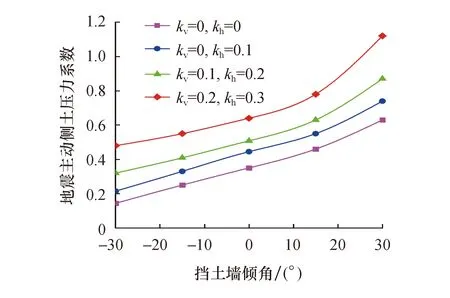
图7 主动侧土压力系数变化关系

4 数值模拟对比分析

4.1 模型的建立

为了进一步验证本文计算方法的可行性,用有限元软件建模对地震作用下挡土墙绕墙趾转动时的土压力分布情况进行模拟.考虑到挡土墙横截面形状、荷载等沿长度方向基本保持不变,因此建模时将其简化为平面问题,建立二维有限元模型.

该模型由重力式挡土墙、墙后填土和墙下地基三部分组成,墙后土体力学参数与算例分析相同.墙高H=8 m,墙顶面宽1.4 m,墙底面宽3.6 m,墙后土体的长度取5H;墙前地基长度取2H,墙底向下取5H.假设挡土墙为线弹性模型,土体本构关系采用Mohr-coulomb屈服准则.挡土墙和土体的接触采用ABAQUS系统中定义的黏结模型,在Interaction模块中Type选项选择Contact,在对话框定义粘结材料刚度系数.模型顶部设置为自由边界,底部为固定边界.共产生3 774个单元,3912个节点,挡土墙单元网格为CPE4单元,墙后及下部土体单元网格为CINPE4单元,模型及单元网格划分如图8所示.

图8 挡土墙模型单元网格划分

地震作用的施加通过ABAQUS的黏弹性模型来实现,黏性边界通过在边界上应用预定义好的无限单元实现.模型中为了模拟挡土墙绕墙底转动的位移模式,在边界条件中约束模型底部在y和x方向上的位移.在Load模块,导入已有的地震加速度数据,则可以将地震荷载作为边界条件施加在墙后土体与墙下土体的接触面上,所施加地震荷载加速度时程曲线如图9所示.

图9 地震荷载时程曲线

4.2 模拟结果分析

图10为地震作用下的挡土墙位移云图.从图中可以看出,挡土墙位移自底部到顶部逐渐增大,墙体顶部位移明显大于挡土墙底部位移,且墙趾点产生明显变形,即可以认为挡土墙的位移模式为绕墙趾转动.

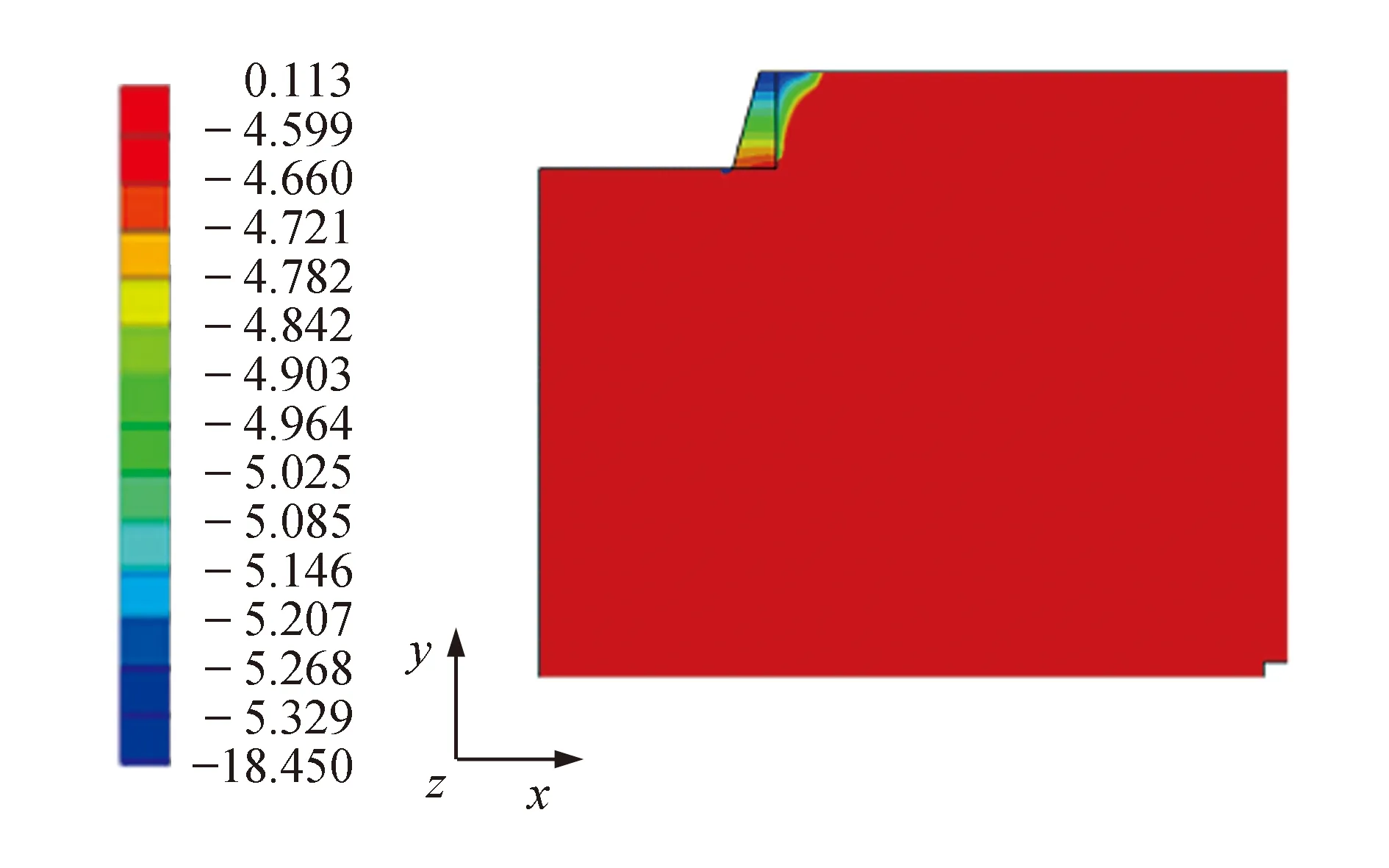
图10 挡土墙位移云图

图11为土压力分布的理论计算与数值模拟结果对比图.从图中可以看出,模拟所得土压力分布结果为沿墙高的非线性分布,在墙后填土表面超载为0的情况下,墙体顶面土压力为0,随着深度增加,土压力逐渐增大,数值模拟土压力值在6～6.5 m之间出现局部下降,从28.95 kPa减小至21.39 kPa,随后逐渐增大,在7 m处达到最大值45 kPa.分析其原因如下:在建模时为实现挡土墙绕墙趾转动的位移模式而限制了墙底水平与竖向两个方向的位移.其次,在有限元软件模拟地震荷载作用下的土压力时,将地震荷载视为一种边界条件,土体在地震荷载作用下由于土颗粒的重分布而出现塑性变形,土体强度刚度发生变化,而Mohr-coulomb模型中土体刚度和强度均为常数.因此导致挡土墙底部出现局部土压力的突变集中现象,表现为图11中模拟所得曲线中距墙顶6～7 m处土压力小范围下降后的急剧上升的现象.从图11可以看出,模拟所得土压力曲线整体变化趋势与计算值较为相近,结果较为理想.但土压力分布曲线峰值存在差异,模拟所得土压力强度分布曲线上土压力强度最大值比理论计算结果小,这与模拟过程中参数选取、网格划分和边界条件确定等因素有关.

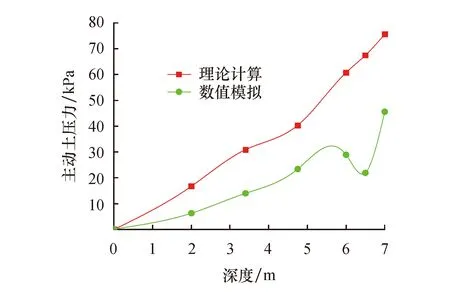
图11 模拟与理论计算对比

5 结论

本文基于水平层分析方法,通过摩擦角随墙体位移变化逐渐发挥的原理建立了绕墙趾转动位移模式下的地震主动土压力计算模型,推导了绕墙底转动位移模式下的地震主动土压力沿墙高的分布、土压力合力及合力作用点高度的理论计算公式.得出如下结论:

1) 挡土墙地震土压力强度分布呈非线性递增分布而并非现行规范规定的三角形分布.土压力分布强度随着地震系数增大而增大,且增幅也随之增大.

2) 最危险滑裂面倾角随着地震系数增大而减小,减小幅度随地震系数的增大而增大.主动侧土压力系数随挡土墙墙背倾角和地震系数的增大而增大.

3) 当水平和竖直两个方向的地震系数均为0时,本文方法计算所得土压力合力作用点高度为0.33H,与Mononobe-Okabe理论一致.但随着地震系数增大,绕墙趾转动位移模式下的土压力合力作用点高度会随之降低.