基于材料损伤演化的钛合金螺旋铣孔切削力仿真模型

李 伟, 周 兰*, 王林军, 安国升, 冯 力, 冯照和

(1. 兰州理工大学 机电工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 省部共建有色金属先进加工与再利用国家重点实验室, 甘肃 兰州 730050; 3. 杭州汽轮机股份有限公司, 浙江 杭州 310022)

钛合金因具有强度高、耐腐蚀性、耐高温的优异性能被广泛应用于航空、医疗、军事等领域[1].然而,由于钛合金材料导热率低,弹性模量小,采用传统钻孔加工钛合金时产生的轴向力大、切削温度高,所以加工孔的质量差、加工效率低,刀具磨损严重[2-7].螺旋铣作为先进的制孔方法可有效降低轴向力,大幅提高加工精度,目前已成为航空、航天领域制孔技术的研究热点之一[8].螺旋铣孔最显著的特点是刀具的进给轨迹呈螺旋线形[9-11],如图1所示.在螺旋铣过程中刀具的螺旋运动由3个不同方向的分运动组成,分别是刀具绕自身轴线的自转、刀具绕待加工孔轴线的公转以及沿刀具轴向的进给运动[12-14].螺旋铣孔与传统钻孔相比,切削力轴向分力减小是其主要优势,但由于偏心加工的方式,螺旋铣孔过程出现了径向力,所以其切削力的变化比传统钻孔更加复杂[15].

图1 螺旋铣孔运动学示意图

切削力对制孔精度、质量、加工损伤和刀具寿命等都有着重要影响.传统切削力的研究方法是通过大量实验构建经验模型[16-17]或解析模型[18-19],但当工件材料、工况条件和刀具结构等因素改变时需要重新构建模型,这大大限制了此类模型的适用范围.目前,有限元仿真技术已成为研究切削加工过程的有效方法[20-22],该方法不仅可以预测切削力的大小,还能够预测加工过程的应力场和温度场,进一步实现工艺参数的优化.然而,在对螺旋铣孔进行仿真的过程中,材料损伤演化和网格尺寸的有效控制成为构建有限元模型的难点.一方面,材料损伤的几何分离准则被广泛应用于分析切屑成型过程,但由于该分离准则对临界值的合理设置依赖于经验,且需要预设切屑与工件材料之间的分离线,并不适用于模拟螺旋铣孔加工过程[23],所以有学者提出将物理分离准则应用于螺旋铣孔仿真过程.其中,张恒[24]采用物理分离准则建立了螺旋铣孔有限元模型,通过对单齿刀具一次成屑过程进行模拟,并利用数学模型推导连续进刀后的切削力变化规律,实现了对螺旋铣孔过程切削力进行预测.Ji等[25]采用物理分离准则,进一步提出基于损伤演化与等效塑性位移之间的线性关系,构建三维螺旋铣有限元模型,从而实现切削力和加工应力的预测分析.另一方面,由于螺旋铣过程中轴向进给量和切向进给量皆很小,所以如果网格尺寸与进给量一致,将导致网格数量过多进而大幅增加仿真时间成本.为此,陈哲[26]通过对螺旋铣孔的加工区域网格进行细化,降低网格尺寸过大对切削力仿真结果的影响.刘倩[27]通过增大刀具进给量的方法提高切削力仿真结果的准确性,但仍无法避免由网格畸变引起的切削力大幅波动.

目前,已有的螺旋铣孔仿真模型对材料损伤演化过程涉及较少,且尚未明确给出损伤演化参数的计算方法.同时,由于工件网格尺寸过大,网格畸变严重,所以切削力仿真结果的准确性大幅降低.因此,本文通过分析螺旋铣孔过程中材料的损伤演化特征,改变断裂能的演化方式,计算断裂能参数并进行修正,对工件轴向网格进行细化,以切削力仿真结果为研究目标,对典型Ti6Al4V材料的螺旋铣孔过程进行仿真研究,并将该模型应用于不同齿数刀具的螺旋铣孔切削力预测,可以对不同齿数刀具的磨损和制孔质量研究提供参考.

1 构建有限元模型

1.1 刀具和工件的结构和材料

传统四齿立铣刀在螺旋铣加工中被广泛应用,该刀具在加工稳定性和制孔效率方面优势显著.因此,本文对四齿立铣刀的螺旋铣孔过程进行建模.该刀具主要结构参数如图2所示.其中,刀具直径为10 mm,前角为5°,后角为10°,螺旋角为30°,刀具材料为硬质合金.另外,图2所示的刀具结构也被应用于不同齿数(单齿、二齿和三齿)刀具的螺旋铣孔切削力仿真模型研究中.

图2 四齿立铣刀几何参数示意图

为实现网格细化,提高仿真效率,对工件的厚度进行简化,如图3所示.图中,H1为正常情况的工件厚度,H2为简化后的工件厚度.螺旋铣过程中刀具作周期性运动,刀具运动1个公转周期的螺距为ap,在仿真过程中刀具每公转的螺距ap最大值为0.3 mm.为了保障公转周期内螺旋铣孔切削力的稳定性,简化后的工件厚度大于刀具每公转的螺距ap.工件模型厚度H2为0.35 mm.

图3 工件厚度简化示意图

工件材料为Ti6Al4V,作为典型的高强度材料被广泛应用于航空、航天领域.刀具材料为硬质合金,其化学性质稳定,适用于加工钛合金材料.刀具和工件的材料属性如表1[28]所列.

表1 工件和刀具材料物理属性

1.2 工件材料本构模型

材料本构模型反映了材料在发生塑性变形时流动应力与应变、应变率、温度之间的关系,这也是构建螺旋铣孔有限元模型的基础.本文采用Johnson-Cook本构模型,该模型在金属切削过程中得到广泛应用,适合模拟钛合金切削过程的高温、高应变和高应变率[21,29-31].Johnson-Cook本构方程为

(1)

Zhang等[32]对3种不同本构参数进行切削力仿真,研究表明不同本构参数下切削力仿真结果差异较大,且与实验结果吻合程度不同.本文选择的Johnson-Cook本构参数是基于文献[24]中对Ti6Al4V材料螺旋铣孔的研究,并经过实验验证,参数如表2[25]所列.

表2 Ti6Al4V的Johnson-Cook本构模型参数

1.3 切屑分离准则

本文对材料损伤过程进行分析,采用定义损伤初始和损伤演化来描述材料的失效过程.

1.3.1损伤初始

本文采用Johnson-Cook剪切失效准则作为材料损伤的初始阶段,该准则可以用于模拟大应变条件下金属失效变形.损伤参数q是基于单元积分点的等效塑性应变定义的,当q=1时单元开始出现损伤,即

(2)

(3)

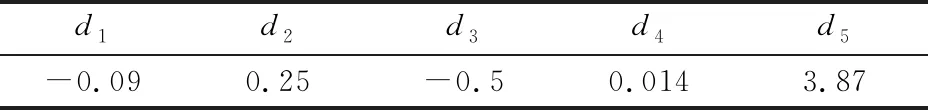
表3 Ti6Al4V的Johnson-Cook损伤参数

1.3.2损伤演化

图4 工件材料变形失效过程应力应变曲线

由图4可以看出,材料在损伤演化阶段的应力应变关系不同于弹塑性阶段,若继续采用弹塑性阶段的应力应变关系则仿真结果会出现较大误差.为了能够表达材料出现损伤失效的行为,Hillerborg等[33]建立应力-位移响应来描述材料出现损伤的软化现象,定义断裂能来表征单位面积材料出现裂纹所需的能量.在损伤演化阶段,以材料的应变能作为失效准则,材料从损伤初始至完全失效采用断裂能描述,即

(4)

基于断裂能的演化方式有线性dc形式和指数db形式,都通过给定演化关系和材料的断裂能Gf对损伤变量进行计算.Zhang等[34]在研究中发现刀具与切屑接触时材料的断裂能演化方式并不是简单的线性演化方式,采用指数演化方式不仅能降低模型对网格的依赖,而且能提高仿真结果的准确性.因此,本文将断裂能的演化方式定义为指数形式,即

在螺旋铣孔仿真过程中网格分离的依据是刀具刀尖能量是否达到所设置的断裂能.仿真过程中如果断裂能设置较小,网格在刀具作用下发生断裂时所需的能量小,网格易断裂且不会产生较大畸变,切屑形态会呈现粒状,切削力和切削温度仿真结果比实验结果低且相差较大,因此断裂能参数的合理选取对仿真结果有着重要影响[34].本文在仿真时对断裂能的设置采用式(7)进行初步计算,将切削力仿真结果与实验结果对比并修正断裂能Gf,直到切削力仿真结果与实验结果达到允许误差范围,即

(7)

式中:KIC为材料的断裂韧度.根据文献[35]Ti6Al4V的KIC为75 MPa/m,初步计算断裂能Gf为43 945 N/m.在此断裂能下切削力仿真结果比实验结果小30%,因此通过增大断裂能可缩小切削力仿真结果与实验结果的误差.经过对比仿真与实验结果对Gf进行修正,Gf最终值为44 350 N/m.若断裂能大于此数值切削力仿真结果会远大于实验结果,并且切削力会发生大幅波动.

1.4 网格划分

刀具接触工件时工件的网格会发生变形,断裂能的设置是网格分离的依据.在螺旋铣仿真过程中,工件网格尺寸的大小对螺旋铣切削力仿真结果具有重要影响[24].螺旋铣刀具轴向每齿进给量在10—3mm以下,切向每齿进给量在10—2mm以下,刀具轴向和切向的进给量小且差异大.图5为切向网格和轴向网格不同取值时网格畸变和应力图.由图5a可以看出:如果将切向网格和轴向网格尺寸同时划分为0.2 mm,那么由于刀具进给量小,在1个网格长度上刀具需要转几周才能删除网格,所以在仿真过程中网格发生严重畸变,从而影响仿真结果的准确性;钛合金螺旋铣孔的应力约为1 GPa[23],加工应力为1.7 GPa,远大于实际加工应力,说明该网格划分与实际工况不符.因此,要对网格进行细化.切向网格尺寸细化为0.1 mm;由于在对轴向网格的细化中发现,若将轴向网格设置小于0.03 mm则网格畸变与切削力仿真结果就会相差较小,但仿真时间大幅增加,所以轴向网格尺寸最终确定为0.03 mm.由图5b可以看出,将轴向网格尺寸划分为0.03 mm,切向网格尺寸划分为0.1 mm,仿真过程中畸变的网格数量明显减少,且加工应力约为1 GPa,符合实际加工情况.

图5 不同网格尺寸下网格畸变和应力图

图6为不同网格尺寸时切削力仿真曲线.可以看出:网格细化前切向和轴向网格尺寸为0.2 mm,网格发生畸变时切削力突变幅度大;与网格细化前相比网格细化后的切削力突变程度大幅减小.工件的网格由307 200个六面体单元组成,刀具的网格由75 000个楔形单元组成,单元类型为C3D4T.

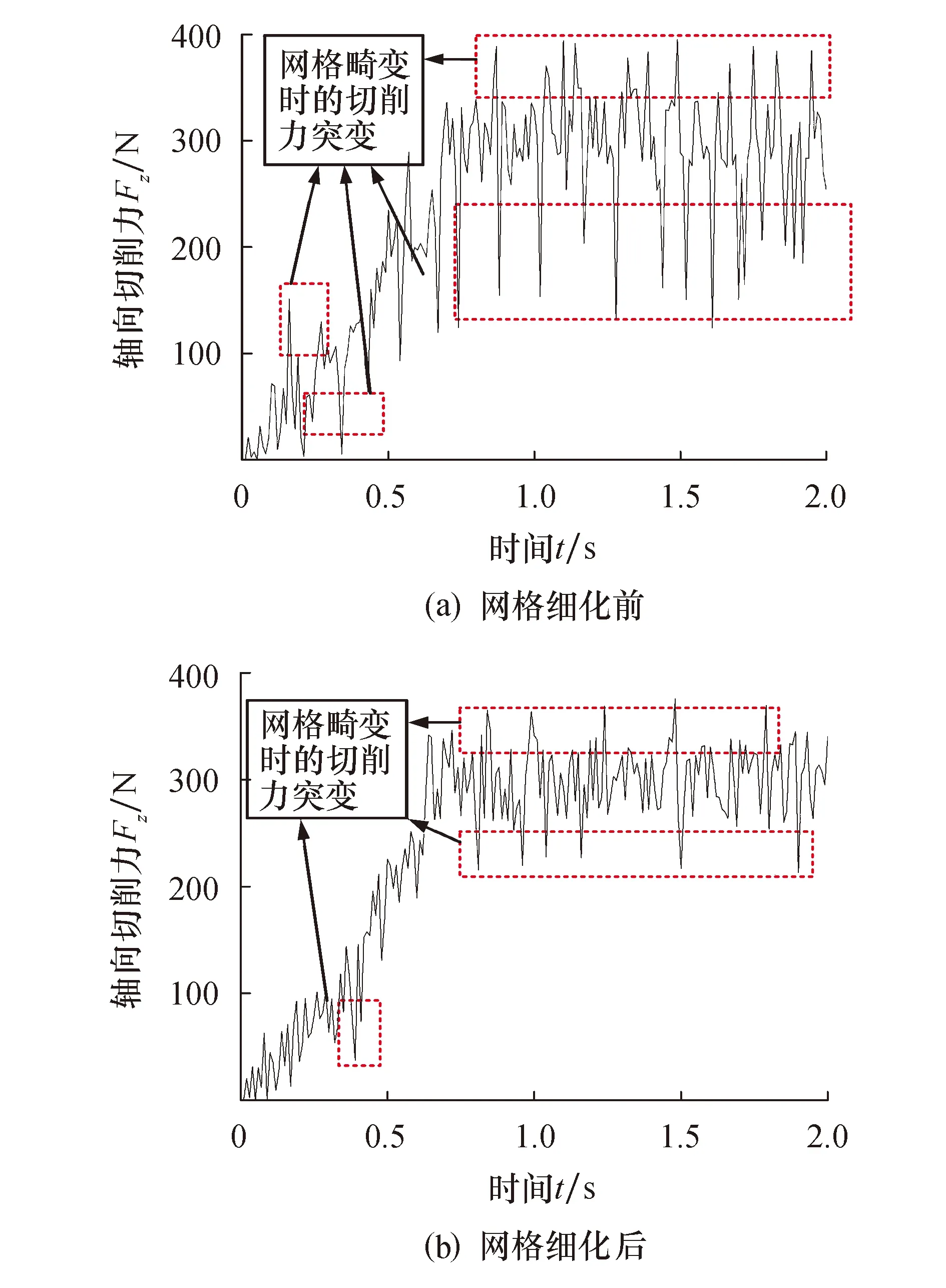
图6 网格细化前后的切削力曲线

1.5 边界条件和摩擦设置

在螺旋铣稳定加工阶段工件保持固定状态.仿真过程中工件的底面和侧面在x、y、z方向的移动被约束,保留刀具沿z方向的移动和旋转,刀具在x和y方向的旋转被约束.刀具在xoy平面的运动表达式为

(8)

式中:ω为圆频率;A0为初始幅值;t0为起始时刻;A1和B1分别为余弦函数和正弦函数的系数.

式(8)以周期性幅值曲线定义,在设置时输入ω、A0、A1、B1的数值即可完成刀具运动的定义.

由于螺旋铣的进给运动分为轴向进给运动和切向进给运动,所以刀具的底刃和侧刃同时发生摩擦.本文采用库仑摩擦模型[25],即

τn=μσn

(9)

式中:τn为摩擦应力;σn为法向应力;μ为摩擦系数.

该模型同时考虑了刀具底刃和侧刃的摩擦.假设刀具上的摩擦应力与法向应力成正比,摩擦系数大小为0.5.

图7为本文建立的三维螺旋铣模型的网格和装配图.图中,工件边长b1=b2=22 mm,加工孔直径D=14 mm,刀具偏心距e=2 mm,工件厚度H2=0.35 mm.

图7 四齿立铣刀加工的三维有限元模型

2 有限元模型对比分析和验证

为了验证本文所建钛合金螺旋铣孔模型的准确性,选择文献[24]的实验结果与线性演化方式仿真结果进行对比.该实验使用浙江大学研发的高精度螺旋铣孔终端执行器进行螺旋铣实验,加工孔直径为14 mm,偏心距为2 mm,刀具直径为10 mm,螺旋角为30°.仿真过程对应的实际加工参数如表4所列.主轴转速、公转速度和螺距对切削力影响的仿真结果与实验结果对比分别如图8～10所示.

表4 仿真过程参数

由图8可以看出:当主轴转速由1 500 r/min上

图8 主轴转速改变时不同断裂能演化方式的切削力仿真结果与实验结果对比

升到3 000 r/min时,指数演化方式的轴向力由144 N下降到98 N,切向力由71 N下降到42 N,轴向力和切向力分别下降32%和41%;螺旋铣孔轴向力和切向力实验值分别下降33%和40%;线性演化方式轴向力和切向力仿真值分别下降35%和24%.

轴向和切向每齿进给量分别为[26]

(10)

式中:fza为轴向每齿进给量;fzt为切向每齿进给量;z为刀具齿数.

根据式(10),随着主轴转速提高,单位时间内刀具轴向和切向每齿进给量同时减小导致切削力下降.然而,无论线性演化方式还是指数演化方式的仿真结果均小于实验结果,原因在于仿真过程中忽略了机床振动、刀具变形以及切屑生成等因素对加工过程的影响[26].基于指数演化方式的轴向力和切向力仿真结果分别达到实验结果的93%和91%,相比基于线性演化方式的85%和82%,主轴转速对切削力仿真的准确性得到明显提高.

由图9可以看出:公转速度由200 mm/min提高到320 mm/min时,指数演化方式的轴向力由117 N上升到150 N,切向力由65 N上升到82 N,轴向力和切向力分别上升28%和35%;螺旋铣孔轴向力和切向力实验值分别上升23%和22%;线性演化方式轴向力和切向力仿真值分别上升29%和16%.

图9 公转速度改变时不同断裂能演化方式的切削力仿真结果与实验结果对比

根据式(10),随着公转速度提高,单位时间内刀具切向和轴向每齿进给量增大导致切削力上升.由图9还可以看出:线性演化方式在240 mm/min时切削力突然下降,原因在于刀具与切屑刚接触时刀尖能量就达到所设置的参数从而导致切削力发生突变;指数演化方式的切削力仿真值变化趋势显然更加接近于实验值,分别达到实验值的91%和92%,而线性演化方式的轴向力和切向力仿真值为实验值的84%和80%.因此由仿真结果表明,本文所建立的模型仿真结果与实验结果契合度很高.

由图10可以看出:螺距由0.15 mm增大到0.3 mm时,指数演化方式的轴向力由82 N上升到181 N,切向力由39 N上升到68 N,轴向力和切向力仿真值分别上升120%和74%;螺旋铣孔轴向力和切向力实验值分别上升126%和69%;线性演化方式轴向力和切向力仿真值分别上升110%和40%.

图10 螺距改变时不同断裂能演化方式的切削力仿真结果与实验结果对比

根据式(10),随着刀具每公转的螺距增大,单位时间内刀具轴向每齿进给量急剧增大导致轴向切削力上升.而刀具轴向进给量增大也导致切向力上升,这表明螺旋铣孔切向力也受到轴向进给量的影响.由图10还可以看出:在刀具每公转的螺距增大时仿真结果与实验结果更接近,原因在于随着螺距增大指数演化方式的网格删除过程更加稳定;采用指数演化方式的轴向力和切向力仿真值分别为实验值的92%和91%.仿真结果与实验结果的对比表明,本文断裂能参数的设置和指数演化方式的仿真值相比线性演化方式更接近实验结果.

综上所述,通过改变加工参数(主轴转速、公转速度、螺距)对切削力仿真并将文献中实验结果与仿真结果对比可知,轴向切削力和切向切削力的平均值为实验值的91.7%和92%,且最大误差不超过9%,由此说明本文所建模型可以用于螺旋铣孔切削力的精准预测.

3 不同齿数下的切削力预测

采用本文构建的有限元模型对不同齿数刀具的切削力变化规律进行仿真.单齿、两齿、三齿、四齿刀具在主轴转速为1 500 r/min,公转速度为320 mm/min,螺距为0.35 mm时切削力仿真曲线如图11所示.图中,Fx和Fy为切向切削始力,Fz为轴向切削力.可以看出:在加工起始阶段(0～0.5 s),刀具开始与工件接触,单位时间内材料切削量迅速增大,因此不同齿数刀具的轴向力和切向力均呈现明显上升趋势;而在稳定加工阶段(0.5～2 s),轴向切削力变化较为平稳,切向切削力曲线存在90°相位差,原因在于刀具在公转运动时进给方向不断变化导致切向力在x和y方向呈现周期性波动,此时切削力的变化周期为刀具的公转周期.刀具齿数是影响切削力大小的重要因素,根据式(10),在相同加工条件下,刀具齿数与进给量呈反比,因此刀具齿数越多切削力越小.

图11中轴向力大小为稳定加工阶段切削力的平均值.为方便与切削量对比,用Fr表示Fx与Fy的合力,关系式为

图11 不同齿数刀具加工的螺旋铣孔切削力仿真曲线

(11)

螺旋铣孔过程中刀具每齿进给量与切削力大小呈线性关系[24].在相同加工条件下,单齿到两齿刀具时每齿进给量下降50%,两齿到三齿刀具时每齿进给量下降32%,三齿到四齿刀具时每齿进给量下降23%.同样,轴向力仿真值分别下降42%、24%、20%,切向力仿真值分别下降40%、22%、17%.不同齿数刀具切削力的大小与每齿进给量变化呈线性关系,由此说明本文建立的模型适用于预测不同齿数刀具的切削力.

4 结论

本文通过对材料的损伤演化过程进行分析,确定了断裂能参数;并对工件的轴向和切向划分不同尺寸的网格,建立三维螺旋铣孔有限元模型;通过改变加工参数对切削力进行仿真分析,并与相对应的螺旋铣孔实验结果进行对比.得到以下主要结论:

1) 定义损伤初始和损伤演化描述工件材料的失效过程,将断裂能演化方式设置为指数形式,计算并修正损伤演化参数,确定断裂能为44 350 N/m;通过对网格细化后发现,该模型可以有效降低网格畸变,且加工应力符合实际加工情况.

2) 采用该模型对螺旋铣孔切削力仿真,并与实验结果对比发现,在不同加工参数(主轴转速、公转速度、螺距)下采用指数演化方式的轴向切削力和切向切削力的仿真值比采用线性演化方式的更接近实验结果,指数演化方式的轴向力和切向力平均值为实验值的91.7%和92%,且最大误差不超过9%,由此说明该模型可以用于螺旋铣切削力预测.

3) 采用该模型在不同齿数刀具(单齿、两齿、三齿、四齿)下加工,刀具齿数增加而切削力下降,且刀具切削力的下降幅度与每齿进给量的减小幅度保持一致,切削力仿真结果可以为螺旋铣孔加工中不同齿数刀具的磨损和孔加工的质量提供参考.