思维培育有方法 数学模型记心间

文／王磊

从学习数学的时间轴上看，通透了解数学模型，深度掌握解题方法，有效培养数学思维，远比会解一道题重要得多。下面，我们通过几道例题，感受与三角形有关的四种数学模型。

一、“手拉手”模型的解题策略

“手拉手”模型的典型特征是两个三角形的一个顶点相互重合，通过旋转等图形变化后，可形成一些结论和规律。

例1如图1，在△ABC中，AB=CB，∠ABC=90°。D为AB延长线上的一点，点E在边BC上，连接AE、DE、DC，AE=CD。

求证：∠BAE=∠BCD。

图1

【解析】本题中，要证明∠BAE=∠BCD，我们只需证明出△ABE≌△CBD即可。题干已经告诉我们AB=CB、AE=CD、∠ABC=90°这三个条件，我们可以通过“HL”来证明。

其实，该模型可以探究的地方还有很多。比如AE与CD的位置关系（提示：AE⊥CD），这也是考试中常遇到的问题。同学们可以试着猜想和证明一下。

二、“动点”问题的解题策略

“动点”问题的难点就在于点位置的灵活性。遇到这类问题，只要根据“轴对称的性质”“两点之间，线段最短”等知识，将动态转变为静态，就可巧妙地解决这类问题。

例2如图2，在等边三角形ABC中，AB=4，P是BC边上的动点，Q是BA边上的动点，H是AC边上的动点，则△PQH周长的最小值为________。

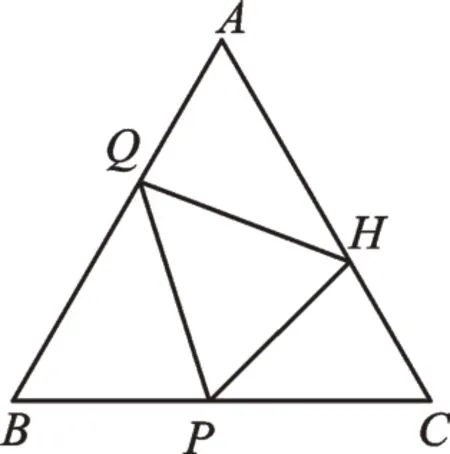
图2

【解析】△PQH三条边的长度在不断变化，这给我们的解题带来了极大的困难。我们可以作点P关于AB的对称点M，以及点P关于AC的对称点N，如图3，则根据轴对称的性质，得到QP=QM，HP=HN。根据“等量代换”，得QP+PH+QH=QM+QH+HN。连接MN，根据公理“两点之间，线段最短”，可知QM+QH+HN的最小值就是线段MN的长，所以△PQH周长的最小值为MN。当点P为BC的中点时，MN最小，MN=BC=6。

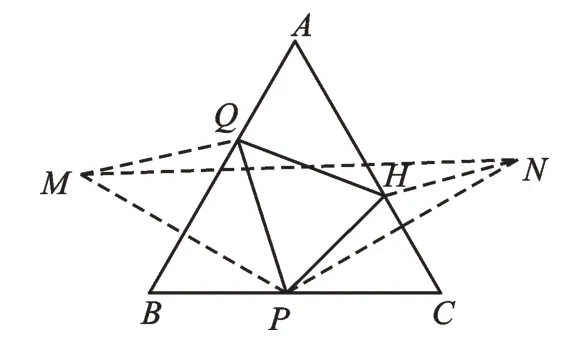
图3

三、“一线三等角”问题的解题策略

“一线三等角”问题的特征是在一条线的同侧或异侧，有两个全等或相似的三角形。在这样的组合图形中，蕴含了成比例、相等、互余等关系。

例3如图4，E是正方形ABCD的边AB上的动点，EF⊥DE交BC于点F。

（1）求证：△ADE∽△BEF。

（2）设正方形的边长为4，AE=x，BF=y。当x取什么值时，y有最大值？并求出这个最大值。

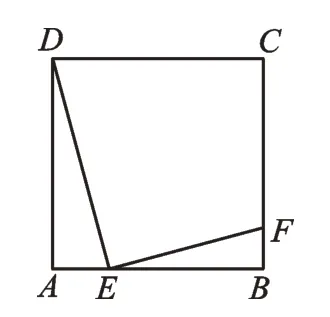
图4

【解析】（1）要证相似的这两个三角形中，已知的条件有∠DAE=∠EBF=90°，那么只要得出另外一组对应角相等即可。因为∠ADE+∠DEA=90°，而∠AED+∠FEB=90°，所以∠ADE=∠FEB，如此就满足了两个三角形相似的条件。在（2）中，可用x表示出BE的长，然后根据（1）中△ADE∽△BEF可得出比例关系式，然后就能得出一个关于x、y的函数表达式。根据函数的性质即可得出当x=2时，y有最大值，最大值为1。

四、“瓜豆”问题的解题策略

“瓜豆”问题的特征就是一个主动点，一个从动点。从动点受到某种条件的约束，跟着主动点动。当主动点发生运动时，从动点的轨迹与主动点的轨迹相同或相似，且运动轨迹长度的比和它们到定点的距离比相同。

例4如图5，△ABC中，∠ACB=90°，CA=CB=4，CD⊥AB于点D，P是CD上一个动点，以P为直角顶点向下作等腰直角△PBE，连接DE，求DE的最小值。

图5

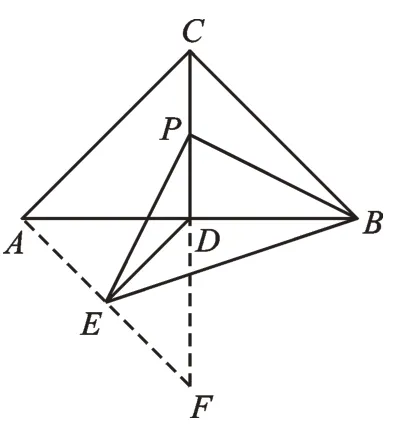
图6

【解析】通过观察和推理，我们可以发现，点E的运动轨迹是一条线段，也就是图6的AF。当点P在C点时，点E在A点；当点P到达D点时，点E在D的下方，且长度等于CD。因此，DE的最小值就是Rt△ADF斜边上的高，DE的最小值为2。