一道函数题的衍生与延展

文／姜鸿雁

再复杂的问题都是由简单的、基本的问题演变而来的。同学们只要立足基本知识和基本技能，把握基本数学思想，注意积累基本活动经验，便可以“以不变应万变”，下面以一个例子来说明。

【题根】在平面直角坐标系xOy中，有A（2，-3）、B（-1，0）、C（0，-3），分析并解决下面的系列问题。

一、三个定点完成“基本框架”

【要求1】提一个关于反比例函数的问题，并解决它。

【问题1】求过点A的反比例函数表达式。

【解析】反比例函数图像与坐标轴没有公共点，只能通过点A提相关问题。运用待定系数法，可得反比例函数的表达式为y1=-（为了后续研究的方便，记作函数“y1”）。

【要求2】运用其中两个点提出关于一次函数的问题，并解决它。

【问题2】求过A、B两点的一次函数表达式。

【解析】根据一次函数的概念，可以选择点A和点B或点B和点C，我们这里选择求过点A和点B的一次函数表达式。运用待定系数法，不难求得y2=-x-1。

【问题3】结合问题1、2的结论，试写出当y1＜y2时自变量x的取值范围。

【解析】联立两个函数表达式，求出两个函数图像的另一个公共点坐标为（-3，2），结合函数图像的相对位置（如图1），可得当x＜-3或0＜x＜2时，y1＜y2。

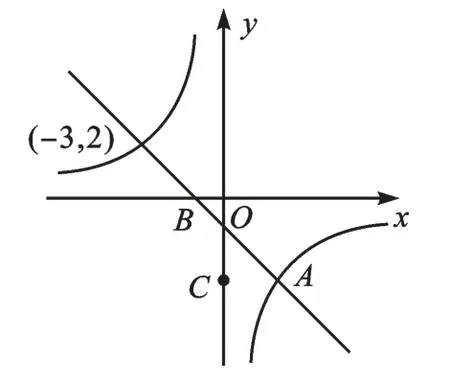
图1

【说明】同学们在问题2 中，如果选择过点B、C的一次函数表达式，除了可以提出类似的问题3，还可以提出与面积有关的问题，试试看吧！

【要求3】根据A、B、C三个点的坐标，提出一个关于二次函数的问题，解决之后，说说你对这个二次函数及其图像的认识。

【问题4】求过A、B、C三点的二次函数表达式，并说明该二次函数的图像及性质。

【解析】我们可以设一般式：y=ax2+bx+c（其中a、b、c是常数，a≠0），代入三个点的坐标，解关于a、b、c的方程组，即可求得函数表达式。仔细观察三个点的坐标特征，由A（2，-3）、C（0，-3）不难发现，此二次函数图像的对称轴是直线x=1，所以可以设顶点式：y=a（x-1）2+k，将点B、点C坐标代入即求得a=1，k=-4，所以二次函数的表达式是y=（x-1）2-4，即y=x2-2x-3。如图2，二次函数图像开口方向向上，顶点坐标为（1，-4），对称轴是直线x=1。当x＜1 时，函数值y随自变量x的增大而减小；x＞1 时，函数值y随自变量x的增大而增大；当x=1时，函数y有最小值为-4。进一步观察图像，我们还发现，方程x2-2x-3=0 的两个根分别为x1=-1，x2=3；当-1＜x＜3 时，y＜0，当x＞3或x＜-1时，y＞0；等等。

图2

【归纳】待定系数法是求函数表达式最基本、最重要的方法。求二次函数的表达式时，根据已知条件，选择最合适的表达形式，可以达到事半功倍的效果。利用函数图像分析函数的性质以及函数与函数、函数与方程、函数与不等式等之间的关系，可以让这些相对抽象的数量关系在函数图像的表征下，变得直观而又具象。

二、一个动点犹如“源头活水”

如图3，若问题4 中的二次函数y=x2-2x-3与x轴的另一个公共点为点D，设点M是第四象限图像上的一个动点，过点M作y轴的平行线，交直线CD于点N，连接DM、CM。

图3

【要求4】在点M的运动过程中，图3中有哪些量随之发生变化，由此，能提出什么问题并解决它？

【问题5】线段MN的长随M点位置的变化而变化，求它的最大值。

【解析】揭示MN的长与点M位置之间的变化规律是解决问题的根本。首先，不难求得直线CD的函数表达式为y=x-3；其次，设点M（m，m2-2m-3），则点N（m，m-3），得MN=-m2+3m（0＜m＜3）。MN的长与m之间是二次函数关系，配方，得，当m=时，MN取最大值，最大值为。

【问题6】△DMC的面积随M点运动变化而变化，求△DMC面积的最大值。

【变式1】以MN为直径的圆与CD相交于点P，求弦NP的最大值。

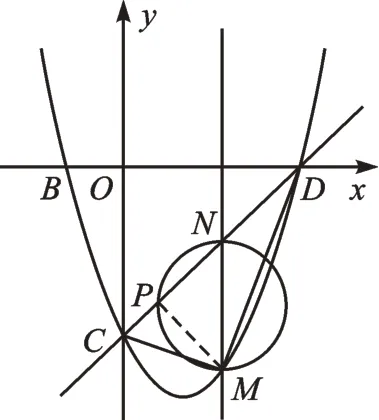
图4

【变式2】如图5，连接BM，交直线CD于点Q，求的最大值。

图5

【解析】因为△CQM与△CQB同高，所以。在平面直角坐标系中，常常将不平行或不垂直于坐标轴的线段向平行或垂直于坐标轴的方向转化（不妨称为“化斜为直”）。点B、直线CD分别为确定的点、确定的直线，则过点B作y轴的平行线交直线CD于G（如图6），不难有BG=4。易证△QNM∽△QGB，则，所以当MN取

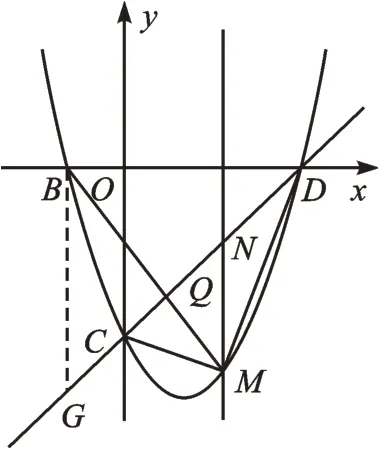
图6

【归纳】点M位置的变化，导致线段MN的长、△DMC的面积、弦NP的长、等的变化，由此可以分别建立点M的横坐标与这些量之间的二次函数关系，这就是建模的过程。随着解决问题的深入，结合相似三角形、三角函数等知识，我们不难发现，当MN取最大值时，相关的量随之取得最大值，这是化陌生为熟悉的过程，更是“会一题、通一片”的状态。

掌握扎实的基本知识（待定系数法求函数表达式、相似三角形、三角形函数等）和过硬的基本技能（识图、构造、运算等），灵活运用基本思想（建模、数形结合、转化等），注意积累基本经验（求MN的最大值的基本活动经验是本题系列变式的基础）是我们学好数学的强大后盾。同学们，本题还可以提出若干问题，去试试吧！