心电信号抑噪算法的研究

梁伯虎 石翠萍 于泓博

摘要：基于卡尔曼滤波和平滑滤波相融合的方式，获得滤除工频干扰和肌电干扰的解决方案。平滑滤波主要滤除工频干扰，将平滑滤波后的心电信号以自回归模型的方式进行心电信号建模，并且导入卡尔曼滤波的状态方程和观测方程，完成卡尔曼滤波，可以有效地滤除肌电干扰。根据仿真实验的结果，基本实现从心电信号中滤除工频干扰和肌电干扰。

关键词：心电信号；平滑滤波；卡尔曼滤波

一、前言

由于人们生活节奏的加快，心脏疾病成为威胁人类健康的一大杀手。心电信号能客观反映心脏的生理信息，因而成为诊断和治疗心脏疾病的重要参考依据。但是在采集心电信号时，往往受到患者身体状况、周边环境和采集仪器等因素的影响。这些干扰会使心电信号的信噪比被降低，发生信息丢失或产生虚假信息[1]。因此，本文研究基于卡尔曼滤波和平滑滤波的心电信号抑噪算法，以滤除噪声而又不失真的保留原始信号的细节特征为目标，设计相对高效的滤波系统。

二、抑噪算法的总体设计

选择心电信号的仿真数据。采用麻省理工学院和Beth Israel医院联合提供的MIT-BIH心律失常数据库的心电数据作为仿真数据。MIT-BIH库的心电数据权威而且充分[2]。

仿真心电观测信号。在分析心电信号的特点，以及对噪声和干扰充分认识的基础上，选择两种对心电信号影响较大而且较难滤除的噪声—工频干扰（一种幅频特性接近于频率是50Hz的正弦波干扰）[3]和肌电干扰（一种近似于白噪声的干扰）[4]，叠加在MIT-BIH库的心电数据上，仿真心电观测信号。

针对心电信号中存在的工频干扰，采用平滑滤波算法进行滤除。

建立心电信号的数学模型。将平滑滤波后的心电信号，基于递推最小二乘算法建立心电信号的自回归模型，推导出卡尔曼滤波算法的状态方程和观测方程。

针对心电信号中存在的肌电干扰，采用卡尔曼滤波算法进行滤除。

对卡尔曼滤波和平滑滤波后的心电数据进行分析。采用心电图各个波段的可识别度进行定性评价指标；采用信噪比、相关系数和均方误差作为定量评价指标。

（一）心电信号的仿真数据

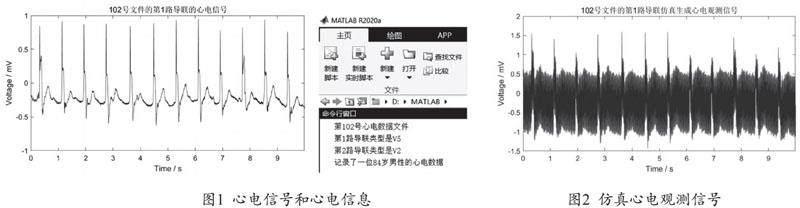
本文选取MIT-BIH库中第102号心电数据的第1路导联的前3600个采样点作为仿真数据，称为净信号。利用MATLAB软件仿真出心电信号和心电信息，如图1所示。

（二）仿真心电观测信号

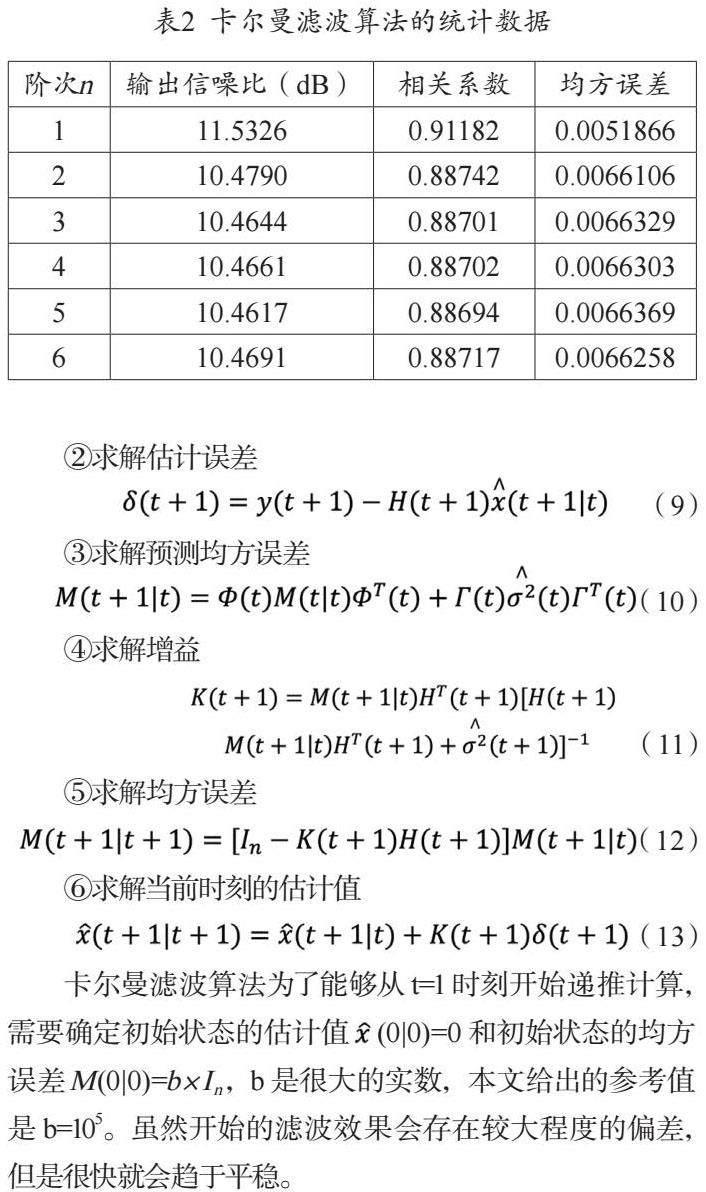
在充分掌握工频干扰和肌电干扰特点的前提下：以频率是50Hz，幅值是心电信号峰—峰值乘以0.5的正弦波作为工频干扰的仿真噪声源；以均值为零，方差为心电信号峰—峰值的平方乘以0.01的高斯噪声作为肌电干扰的仿真噪声源，将这两种噪声源同时叠加在净信号上，以实现心电观测信号的数学仿真，如图2所示。

（三）平滑滤波算法

平滑滤波算法的具体操作步骤如下：采用当前时刻的心电数据和当前时刻之后的M-1个时刻的心电数据，做数学期望，将得到的数据作为当前时刻滤波后的心电数据。

心电信号的采样频率是360Hz，工频干扰的频率是50Hz，所以工频干扰的一个周期影响心电信号的7～8个采样点。而在一个工频干扰的周期内，它的数学期望接近于零。因此，平滑滤波算法M值的参考取值范围在7～8之间。通过实验对比不同M值对平滑滤波后的心电信号的影响，根据表1进行定量分析：当M=7时，滤波后的心电信号输出信噪比和相关系数最高，均方误差最小，说明最接近于净信号。所以，当M=7时，平滑滤波效果最好。

（四）心电信号的自回归模型

将平滑滤波后的心电信号建立自回归模型。

心电信号的自回归模型表达式：

n是自回归模型的阶次。

在已知心电信号的情况下，求解心电信号的自回归模型参数就归结为求解自回归模型的阶次和加权系数以及系统噪声。

1.阶次的确定

通过仿真实验，在后文给出合适的阶次。

2.加权系数的确定

递推最小二乘算法能够根据输入数据进行自回归模型加权系数的调整和修正，使其最大限度地接近于真实值，它的收敛速度和健壮性都比较好，计算量和数据存储量也相对较小，而且对心电信号的先验统计特性要求不高。因此，本文采用递推最小二乘算法对心电信号的自回归模型进行加权系数的确定。递推最小二乘算法公式如下：

初值P（0）=a×In，a是很大的实数，本文给出的参考值是a=105，In是n阶的单位向量；θ （0）=0；y（t）=0 （t≤0）。

通过式（2）和式（3）的递推计算，可以得到各个时刻心电信号在自回归模型中的加权系数，并且截取收敛后的ai值作为所有心电信号的加权系数。

3.噪声方差的确定

综上所述，心电信号自回归模型的参数可以根据以上式子全部递推得到。完成整个建模的过程，为后续卡尔曼滤波计算奠定基础。

（五）卡尔曼滤波算法

本文采用卡尔曼滤波算法滤除肌电干扰。卡尔曼滤波算法将系统的状态方程和观测方程相结合，随着下一时刻心电信号的到来，能够比较准确地计算出下一时刻系统的估计值。状态方程是描述状态变化规律的方程，它记录了相邻时刻状态转移的变化规律。观测方程是描述不同时刻心电信号变化的方程。卡尔曼滤波算法不断地通过“预测—实测—修正”对带有噪声干扰的心电信号进行递推，得出每一时刻的最优估计值，可以有效地消除噪声的干扰。

1.卡尔曼滤波算法的状态方程和观测方程

心电信号的自回归模型可以通过推导，得到卡尔曼滤波算法的状态方程和观测方程。

2.卡尔曼滤波算法的步骤

利用得到的自回归模型、状态方程和观测方程，带入下面公式，完成卡尔曼滤波[5]。

卡尔曼滤波算法为了能够从t=1时刻开始递推计算，需要确定初始状态的估计值 （0|0）=0和初始状态的均方误差M（0|0）=b×In，b是很大的实数，本文给出的参考值是b=105。虽然开始的滤波效果会存在较大程度的偏差，但是很快就会趋于平稳。

根据常用自回归模型的阶次n=1～6的取值范围，分别用上述方法进行卡尔曼滤波仿真。滤波后的统计数据如表2所示。

从表2可以看出：当n=1时输出信噪比最大，相关系数最高，均方误差最小，说明此时对噪声的抑制能力最强，输出信号与净信号的相关程度最高，输出信号最接近于净信号。所以，由实验结果得出，当自回归模型的阶次等于1时，卡尔曼滤波效果最好。

（六）实验分析

为了说明滤波算法对不同的心电信号都有很好的滤波效果，本文利用MIT-BIH库中的心电数据，进行了充分的仿真实验。根据实验结果：图3左图是滤波后的心电信号，针对此波形与净信号（图1）进行定性的对比分析，可以得出滤波算法基本滤除了干扰造成的毛刺；图3右图是从滤波后的心电信号中任意截取一小段心电信号，可以看出较完整地保留了净信号各个波段的细节信息；从表3滤波前后性能指标统计的平均值，经过定量分析可以得出，滤波后的平均输出信噪比和相关系数得到明显的提升，说明滤波后的输出信号与净信号的相关程度比较高；滤波后的平均均方误差有明显的下降，说明滤波后的输出信号比较接近于净信号。因此本文所采用滤波算法的输出数据与净信号吻合度相对较高，证明滤波算法对噪声的抑制能力较强。综上所述，卡尔曼滤波和平滑滤波能够比较有效滤除工频干扰和肌电干扰。

三、结语

随着医疗技术的不断发展与革新，加强对心电信号抑噪算法的研究愈发显得格外重要。本文使用MIT-BIH库的心电数据作为仿真实验的数据，对心电图各个波段的可识别度作定性评价，并且以信噪比、相关系数和均方误差作为滤波算法的定量评价指标，充分验证了滤波算法的有效性。 同时也希望通过相关研究工作的开展，更好地助力于今后滤除工频干扰和肌电干扰工作的升级。

参考文献

[1]赵博特.心脏病史与首发卒中预后的相关性研究[J].中国临床保健杂志，2022，25（5）：619-623.

[2]梁伯虎.基于Matlab的MIT-BIH心电信号读取与波形显示的实现[J].中国电子商务，2011（11）：113.

[3]孙京霞.一种抑制心电信号50Hz工频干扰的改进Levkov方法[J].航天医学与医学工程，2000，13（3）：1-5.

[4]张长胜.AN-CEEMD算法对心电信号中肌电干扰的降噪研究[J].昆明理工大学学报（自然科学版），2020，45（6）：60-66.

作者单位：齐齐哈尔大学通信与电子工程学院