5G网络环境下的“无人机+车辆”应急物资配送优化方案

刘苏晴

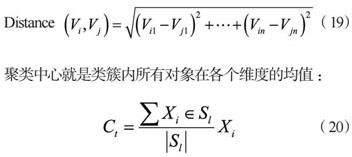
摘要：随着我国5G技术的高速发展，相较于以往的车辆运输，无人机在路面交通不畅的灾后现场配送能够有效降低灾区人员伤亡及财产损失，但同时其具有负载小、成本高等短板。因此配送车量与无人机联合配送模式下的路径优化问题将是研究重点。在满足车辆载重、无人机飞行距离和无人机载重的约束条件下，将完成一次整体配送所需时间作为衡量因素，建立分别在“配送车辆”运输模式和“配送车辆-无人机”运输模式下的最优路径模型对模型进行求解。

关键词：VRP模型；FSTSP模型；选址问题；K-means聚类算法；遗传算法

一、前言

近年来，国内外相关文献主要集中于数学建模和分配模型的求解优化两个方面。颜瑞[1]等根据车辆限行和空域禁飞的情况，将区域限制因素嵌入到模型的构建当中。彭勇[2]等在疫情背景下，以配送商品时间最短为优化目标，设计混合邻域搜索算法求解无人机为多个客户无接触配送的路径问题。为进一步求解数学模型，许多数学者均采用改进的优化算法进行求解。王新[3]等为提高客户的满意度，综合考虑无人机站点和客户时间窗要求，建立以总成本最小化为目标的问题模型，并设计自适应大规模邻域搜索算法进行求解。邓永蕤[4]等在自然灾害情境下建立配送车量与无人机联合配送冷链物流优化模型，采用进化逆转操作，并设计改进的遗传算法。李妍峰[5]等改进变邻域搜索算法求解需求可拆分的路径问题。曹英英[6]等利用遗传模拟退火两阶段算法求解集群下的配送车量与无人机联合配送问题。分为两步提出新型优化迭代算法进行路线的规划。

基于此，我们建立分别在“配送车辆”运输模式和“配送车辆—无人机”运输模式下的最优路径模型，并通过一系列算法对所建立的模型进行求解。

二、模型的建立与求解

（一）模型一的建立与求解

因为配送车辆必须给所有地点配送完应急物资后并返回出发地才是一次整体配送，所以配送车辆必须经过每个地点至少一次，故该问题可简化为：VRP模型。我们假设配送车辆行驶平均速度为50公里/时，为一定值，故可以将完成一次整体配送的时间最少通过：S=VT转化为路程最短。设配送路线连通图为G=（V，E）；顶点集为V={V1，V2，V3，V4…V14}；边集为E；各顶点间的最短距离为dij（i， j=1，2，3…14）；决策变量：                                           。由于我们将判定方案的最优条件从时间最短转化成了路程最短，故目标函数为：

模型中（2），（3）保证了对于每个地点而言，仅有一边进和一边出，（4）消除了子回路对模型的影响，（5）为决策变量的取值约束。对该模型我们使用MATLAB对其进行求解。由于我们需要先求出任意两个地点间的最短距离dij。所以我们采用Floyd算法对VRP模型的求解做好准备。通过Floyd算法计算图1中各个顶点的最短路径时，需要引入两个矩阵，矩阵S中的元素aij表示第i个顶点到第j个顶点的距离。矩阵P中的元素bij，表示顶点i到顶点j的中间点代数。由于模型一中顶点个数为14，则需要对矩阵D和矩阵P进行14次更新。在得到dij的距离矩阵之后，我们采用二边逐次修正法来计算最优路径。我们先设定一个任意的回路：

最短的路程之和为：582公里；所需的完成一次完整的配送工作的最短时间为：11.64小时；最优路径方案为：9—13—14—10—6—4—6—5—2—3—5—7—1—11—12—8—9

（二）模型二的建立与求解

模型一的最优方案会有路径重复，在采用了“配送车辆+无人机”的配送模式后最理想的情况为：配送车辆和无人机的配送路径无重复且完成一次整体配送的时间最短，把该模型看作对模型一的路径优化，但加入了第二种配送工具且两种配送工具之间存在约束关系，故我们可将模型二看作是FSTSP模型。对于无人机的最大路程而言：其平均飞行速度为75公里/小时，单次最长飞行时间为70分钟，所以无人机最长飞行距离为：                    公里。

因为本题采用“配送车辆+无人机”的配速模式，时间上存在重叠部分，所以不能使用最短路程作为方案设定的目标函数，应该采用完成一次整体配送所需的最短时间作为判定标准，假设：C={1，2…14}为顶点集；Cr={r1，r2…rn}为可由无人机配送的地点集；C0为配送车辆可达点+起始点C9；Cd为配送车辆可达点+终止点C9。

由于本模型中的起始点和终止点均为C9，故设C0，Cd对其进行区分。同时假设无人机的飞行路径为F={i，j，k}，其中i为无人机的出发点； j为无人机的配送点； k为无人机的回收点；e为无人机的续航时间；tij1为配送车辆从Ci到Cj所需时间；tij2为无人机从Ci到Cj所需时间；Tj1为配送车辆到达Cj的时间；Tj2为无人机到达Cj的时间。

通过上述分析，我们可以得到目标函数：

由于理想情况为配送车辆和无人机没有路径重复，故我们将其转化为配送车辆和无人机所服务的地点不重复，为了保证每一个地点都必须被配送到物资，故我们约束：

与模型一类似，我们需要先通过Floyd算法分别求出配送车辆和无人机到达任意两个地点之间的最短路程dij。我们在对无人机的路程求解时，考虑到无人机的最长飞行路程为87.5公里，所以我们将超过了87.5公里的路程设为一个无穷大的数。并且由于无人机需要返回到配送车辆上进行充电，这期间存在一段由无人机等待车辆或者由车辆等待无人机的时间，所以我们将无人机的配送路径进行筛选，进行子回路的消除，删除等待时间过长的无人机路径回路，最终得到无人机和配送车量的最佳配送地点范围。

在此之后，我们采用遗传算法对所建立的FSTSP模型进行求解。由于在求解的过程中，会存在局部最优解或者最优解不唯一的情况，所以我们假设种群数目为80，迭代数为5e2次，用提高迭代次数和种群数目的方法避免这种情况的发生。

完成一次完整的配送工作所需的最短时间为：6.28小时；配送车辆的路线为：9—8—7—5—2—5—6—10—9；无人机的路线为：9—13—8、8—12—7、7—11—1—2、6—3—4—10、10—14—9。即：配送车辆在地点9放出无人机后到达地点8，无人机从地点9经过地点13，在地点8被收回；配送车辆在地点8发出无人机后到达地点7，无人机经过地点12后在地点7被收回；配送车辆在地点7发出无人机后经过地点5到达地点2，无人机经过地点11、地点1后在地点2被收回；配送车辆带着无人机从地点2经过地点5到达地点6；配送车辆在地点6放出无人机后到达地点10，无人机经过地点3、地点4后在地点10被收回；配送车辆在地点10放出无人机后，回到物资集中点9，无人机经过地点14后返回到物资集中点9被收回。

（三）模型三的建立与求解

由于当日总需求量为762千克大于500千克，故在配送过程中配送车辆必须至少返回应急物资集中点一次，所以可以看作是对模型二的变形。模型二中，我们已经给出了一种不返回应急物资集中点条件下的最优路径方案，故我们选择将该方案中的各地点进行聚类，将这14个配送地点（包括应急物资集中点在内）分成两类，并且这两部分的总物资重量需要小于500千克。我们可以对传统的K-means聚类算法进行改进，对配送地点进行聚类，采用距离进行相似性评估。用Distance（Vi，Vj）表示两对象间欧式距离，计算公式如下，其中n为对象个数，本题中n为14。

聚类中心就是类簇内所有对象在各个维度的均值：

其中，Ct表示第l个聚类中心， | Sl |表示第l个类簇中对象的个数，Xi表示第i个对象。在对于该模型的求解过程中，由于本模型与模型二初始条件相同，所以同样需要先用Floyd算法求出配送车辆和无人机的最短路程，并对无人机的路径回路进行筛选，得到配送车辆和无人机的可行路径集合。

由于车辆的最大载重为500千克，通过一次运输无法完成配送，所以我们采用K-means聚类算法对已知地点进行分类。配送车辆只需返回到应急物资集中点一次即可完成所有物资配送。故令算法中的k=2，表示将其分为两类。采用遗传算法对其进行求解。通过第一次的求解，我们得到：配送车辆的路线为：9—10—9，无人机的路线为：9—6—10、10—4—3—4—10、10—14—9，具体路径如图1。

其中红色箭头代表无人机的路径，蓝色箭头代表配送车辆的路径。通过第二次的求解，我们得到：配送车辆第二次的路线为：9—5—2—5—7—8—9，无人机第二次的路线为：9—5—2、2—1—11—7、7—12—8、8—13—9。将两次配送路径结合起来，我们得到：

最短用时为7.73小时；配送车辆第一次的路线为：9—10—9，第二次的路线为：9—5—2—5—7—8—9；无人机第一次的路线为：9—6—10、10—4—3—4—10、10—14—9，第二次的路线为：9—5—2、2—1—11—7、7—12—8、8—13—9。

（四）模型四的建立与求解

由于各地当日总需求量：  12+90+24+15+70+18+150+50+30+168+36+44+42+13+41+76+12+16+19+12+33+15+27+13+85+74+120+48+35+180=1552（千克）。

若两辆配送车辆均不多次返回应急物资集中点装物资，则最多配送：500×2=1000（千克），小于1552千克。若两辆车只返回一次，即可装配：500×3=1500（千克），小于1552千克。故至少需要返回两次，即每辆车返回一次或某一车辆返回两次才可完成对所有地点的物资配送，但由于应急物资集中点的位置尚未确定，故我们需要先对其选址进行模型建立。本题采用P-Median Problem模型。假设：C为顶点集；dij为Ci到Cj之间的最短距离；决策变量：

上述模型中，式（21）表示所选取的应急物资点到其他配送点的距离之和最小；约束（22）（23）表示所选的集中点必须服务到所有配送点；约束（24）表示在30个地点中选取2个地点作为应急物资集中点；约束（25）是对决策变量的约束。通过MATLAB对选址模型进行简化运算，我们可以得到应急物资集中点的地址为：地点9、地点20。再通过K-means聚类方法对其进行分类，并对每一部分的FSTSP模型通过遗传算法进行求解，得到结果如表1。

所以在有两个应急物资集中点的条件下，通过“配送车辆-无人机”运输模式对30个地点进行物资配送，完成一次完整的物资配送最优方案所需时间为：9.46小时；

配送路径为：第一辆配送车辆：9—1—11—1—7—8—9，9—5—2—5—6—10—9；第二辆配送车辆：20—25—16—20，20—21—22—27—26—30—26—20；第一架无人机：9—13—9，11—18—11，6—3—4—10，10—14—9；第二架无人机：25—24—19—24—25，25—15—16，22—23—27，27—28—26，30—29—30。

三、结语

通过上述对模型的分析，模型三最具有实用性，故在此我们对于模型三的方案进行检验。在此，我们不将这14个地点进行分类，而将其看作一个整体，经过运算后的结果为：配送车辆行驶路径：9—8—7—5—2—5—9，9—10—14—9；无人机行驶路径：9—13—8，8—12—7，7—11—1—2，5—3—4—10，10—6—9；总配送时间为：6.64小时；误差为：0.93小时。

由于该误差小于1小时，所以方案三具有较高准确度，并且计算速度很快，所以该方案可行，这也同样代表本文所建立的模型正确。

参考文献

[1]颜瑞，陈立双，朱晓宁，等.考虑区域限制的卡车搭载无人机车辆路径问题研究[J].中国管理科学，2022，30（05）：144-155.

[2]彭勇，黎元钧.考虑疫情影响的卡车无人机协同配送路径优化[J].中国公路学报，2020，33（11）：73-82.

[3]王新.车辆和无人机联合配送路径问题研究[D].大连：大连海事大学，2020.

[4]邓永蕤，徐菱，吴茂婷，等.基于无人机与卡车联合运输下的冷链物流网络优化[J].江苏农业科学，2019，47（13）：268-272.

[5]李妍峰，李佳，向婷.需求可拆分的无人机与卡车协同路径优化问题[J].工业工程，2022，25（01）：54-63+143.

[6]曹英英，陈淮莉.基于集群的卡车与无人机联合配送调度研究[J].计算机工程与应用，2022，58（11）：287-294.

作者单位：东北电力大学经济管理学院