考虑动态需求的多中心沿途补货冷链物流配送路径优化

谭晓伟 王雪韵 胡大伟

为提升冷链物流配送效率、降低物流成本，本文在综合考虑多配送中心、客户动态需求、沿途补货策略的前提下，建立以总配送成本和客户满意度最优为目标的冷链物流配送模型.模型采用主目标法处理客户满意度和成本之间的背反关系，将动态问题按照时间轴依次分解为一系列的静态调度子问题并考虑了5种配送成本.本文提出自适应大邻域搜索算法求解该模型，设计了三种破坏算子和三种修复算子，对小中大三种不同规模的算例进行测算.结果表明该算法在速度、精度和稳定性上表现良好，对求解此类问题有较好的适应性和准确性.与不考虑沿途补货策略的动态配送方案相比，沿途补货策略可使成本降低23.06%、客户满意度提升8.69%.结果表明提出的配送方案可很好地节约企业的配送资源、减少配送成本、增强竞争力.

物流工程； 冷链物流； 自适应大邻域搜索算法； 配送路径优化； 动态需求； 沿途补货

U492.3A2023.022002

收稿日期： 2022-08-31

基金项目： 陕西省自然科学基金项目（2021JZ-20）

作者简介： 谭晓伟（1985-）， 男， 内蒙赤峰人， 工程师， 博士生， 主要研究方向为物流优化. E-mail： tanxw@chd.edu.cn

通讯作者： 胡大伟. E-mail： dwhu@chd.edu.cn

Research on distribution routing optimization of multi-center cold chain logistics for replenishment along the way considering dynamic demand

TAN Xiao-Wei1， WANG Xue-Yun2，  HU Da-Wei3

（1. School of Automobile， Changan University， Xian 710018，  China；  2. Daqing Water Affairs Bureau， Daqing 163311， China;

3. School of Transportation Engineering， Changan University， Xian 710064， China）

To improve the efficiency of cold chain logistics distribution and reduce logistics cost， a cold chain logistics distribution model is established to optimize both total distribution cost and customer satisfaction on the premise of comprehensively considering multiple distribution centers， customers dynamic demand and strategy of replenishment along the way. A principal objective method is used to deal with the inverse relationship between customer satisfaction and cost， and the dynamic problem is decomposed into a series of static scheduling sub-problems according to the time axis with five kinds of distribution cost considered. An adaptive large neighborhood search algorithm is designed to solve the peoposed model with three kinds of damage operators and three repair operators. Small， medium and large-scale examples are calculated respectively， the results show that the algorithm performs well in terms of speed， accuracy and stability， and moreover， is adaptable and accurate in solving such problems. Compared with the dynamic distribution scheme without considering strategy of replenishment along the way， the cost is reduced by 23.06% and the customer satisfaction is improved by 8.69% by the strategy of replenishment along the way， this  confirms the proposed distribution scheme can save distribution resources， reduce distribution cost and enhance the competitiveness of enterprises.

Logistics engineering; Cold chain logistics; Adaptive large neighborhood search algorithm; Distribution routing optimization; Dynamic demand; Replenishment along the way

1 引 言

随着人们对生活品质的要求不断提高，生鲜电商迅猛发展、冷藏食品消费量不断升级，冷链物流配送问题日益凸显.生鲜产品保质期短、易损耗，需要冷链物流具有较高的时效性.因此，合理规划配送路径，提高客户满意度的同时，降低配送成本，成为冷链物流的关键问题.

在基于动态冷链物流配送问题的研究方面，Mustafa等［1］建立了综合考虑车辆行驶速度变动和碳排放的数学模型，并设计了遗传算法对其求解，结果发现所提出的模型和求解方法适用于可持续物流决策过程中的许多实际应用场景；王淑云等［2］针对研究的动态蓄冷式多温共配问题，构建了考虑随机需求的以成本最小为目标的数学模型，模型考虑了正向配送和反向补货两种情况；Rajeev等［3］考虑服务订单和服务时间呈概率弹性变化的特点，建立了以运输成本最小和客户满意度最高为目标的数学模型；Reza等［4］研究绿色交通条件下易腐产品的动态绿色车辆路径问题，优化了动态交通网络的总成本，有效减少了环境影响，提高了顾客满意度；林明锦等［5］研究考虑客户需求动态变化和软时间窗的两级路径优化问题，设置合适的概率阈值来调整客户动态度，动态包括客户点新增和需求量变动两种.

在基于沿途补货冷链物流配送问题的研究方面，李延晖等［6］研究了考虑沿途补货的多配送中心车辆路径问题，建立了以运输成本最小为目标的数学模型，设计了带补货控制因子的蚁群算法对问题进行求解，表明沿途补货策略能更有效地利用车辆资源；张景玲等［7］考虑沿途补货的动态路径优化问题，采用自适应免疫量子进化算法，证明了动态条件下沿途补货策略的实用性；Luca等［8］研究了考虑补货的车辆路径问题，当车辆的剩余载重不足以支撑后续服务计划时，车辆选择去仓库补货，通过后续测试发现，选择补货策略的配送方案能提高运输总效率；李国明等［9］研究了客户需求和服务时间都随机改变的车辆路径问题，同时在配送方案中加入补货策略，设计了改进的禁忌搜索算法对问题进行求解，并用6种不同实验对算法进行评估.

在基于多配送中心的物流配送问题的研究方面，Lahyani等［10］使用自适应大邻域搜索算法求解多车场开放式问题，采用多组不同规模数据进行测试，最大为6个配送中心288个客户点，证明了自适应大邻域搜索算法对于求解此类问题的适应性和优越性；Husakou等［11］研究了多车场异构车队开放式路径问题，不同车队的单位运输成本和载重容量不同，模型以最小的运输成本为目标，文章使用标准的混合整数规划求解器求解实例并获得最优解；Sadati等［12］研究多车场绿色路径优化问题，建立了以运输总路径最短为目标的数学模型，设计了禁忌搜索算法和广义变邻域搜索算法相结合的算法，通过测算小规模算例证明了该算法具有较强的鲁棒性；范厚明等［13］研究多配送中心同时配集货路径优化问题，模型考虑包括理货成本在内的三种成本，并设计混合遗传算法对算例进行求解.

通过上述分析可知，目前冷链物流研究文献虽多，但大部分集中于传统静态车辆路径问题和单配送中心固定区域范围配送问题，综合考虑多配送中心和客户动态需求的冷链物流研究较少，考虑沿途补货的文献亦不多.综合考虑客户需求变化情况和多配送中心的配送条件更加贴合冷链物流企业配送的现实场景，同时，考虑沿途补货策略能够节约企业资源，提高冷链物流配送的快速响应能力和配送效率.因此，本文构建了考虑动态需求和沿途补货的多配送中心冷链物流配送模型并设计了相应的自适应大邻域搜索算法对其给予有效求解，旨在提高冷链物流企业的服务能力，提高客户的满意程度.对冷链物流企业控制成本的同时，保持企业核心竞争力有着很大的现实意义和应用价值.

2 问题描述及模型建立

2.1 问题描述

在规定的时间段内，某区域的多个配送中心共同服务一定数量的客户，配送产品为单一的冷链产品，通过对车辆配送路线的合理规划从而满足求解目标.其中客户分为静态客户和动态客户，静态客户指配送开始前一天下单的客户，动态客户指配送开始后，实时出现的新增订单客户.由于可能存在动态客户大量出现后车辆载重不足或原始配送中心缺货等现实情况，车辆允许中途去区域内的任一个配送中心补货.所研究问题的示意图如图1所示.

2.2 问题假设

为了简化问题并保证解决方案的可操作性，假设：（1） 运输时忽略货物的体积、形状等因素，只考虑货物重量对车辆载重的影响；（2） 除了配送中出现的动态订单，其余初始订单的全部信息都是已知的，当动态订单出现时该订单的全部信息随即已知；（3） 车辆是同质车辆；（4） 整个配送体系包含若干配送中心，所有配送中心库的位置已知，所有车辆从配送中心出发，完成配送任务后返回各自的配送中心；（5） 忽略上级向配送中心配备货物的过程，整个配送过程忽略货物在配送中心内的损耗，只计算在车辆运送过程中的货损成本；（6） 每个客户点只被服务一次，客户点的需求不可拆分；（7） 车辆在运行过程中始终处于匀速行驶；（8） 在配送中心补货需要的时间与客户点服务时间一致；（9） 每个配送中心的车辆都是足够的，不存在无法发车的情况.涉及的符号说明如表1所示.

3 算法设计

3.1 求解思路

采用自适应大邻域搜索算法（Adaptive Large Neighborhood Search， ALNS）对该模型求解，具体的算法流程如图2所示.

对于分布在某个区域的多家配送中心而言，首先依据静态客户规划初始路径.在实时服务时间窗口开放时，配送中心将处理陆续接到的新增客户订单需求.考虑到动态问题的复杂性，首先将动态问题分成若干个静态子问题进行简化，本文选择将配送时间窗划分成多个时间片段，每到时间片段的节点时统计一次动态信息，将上一个时间片段内出现的新增客户进行处理，此时整个系统中待服务的客户有初始路径中未完成配送的客户和新增客户两类，如图1所示，配送策略分三种类型.

（1） 路径中某个正在执行配送任务车辆的剩余载重量足以为待服务的客户服务，路径中插入新增客户后全部待服务客户点的时间窗仍然满足，且配送成本低于重新发车的成本，则将新增客户分配给该车辆，车辆更新路径，按照新路径规划依次服务.

（2） 路径中某个正在执行配送任务车辆的剩余载货量不足以为待服务的客户服务 ，此时车辆可以选择去临近的配送中心补货，当补货完成后足以为待服务客户配送并且仍满足路径中所有待服务客户的时间窗要求且配送成本比重新发车低，则将新增客户分配给该车辆，车辆更新路径，按照新路径规划依次服务.

（3） 路径中任意车辆剩余载货量不足以为待服务的客户服务，且任意车辆去临近配送中心补货后无法满足后续待服务客户时间窗要求，或者任意车辆给新增客户服务的成本都高于配送中心单独发车给新增客户服务的成本，此时配送中心新派车辆对新增客户进行服务，已出发的车辆按照原规划路径进行配送.

3.2 初始解的构造

使用构造方法产生初始解.首先对客户点进行随机排序，然后在满足载重约束、时间窗约束的情况下当遇到可行插入的位置时将客户点插入，随即产生问题的初始解Sinitial，然后在该初始解的基础上进行固定次数的迭代，迭代过程中使用破坏和修复算子进行邻域搜索.初始解构造的基本流程如下.

Step1：将待安排的客户进行随机排序得到客户集合B，输入当前的线路数据，当没有进行动态更新时当前线路为空集，开始更新时，当前线路数据为上一个周期优化结束后线路去除可重新安排的客户点的剩余线路；

Step2：为客户集合B中的第一个客户i寻找当前周期新增车辆中满足所有约束的插入位置，若存在，将客户点插入后更新线路并进入Step5，反之进入Step3；

Step3：为客户i寻找上周期使用的车辆中满足所有约束的插入位置，若存在，将客户点i插入后更新线路并进入Step5，反之进入Step4；

Step4：找到距离客户i最近的配送中心发车形成新的线路，并进入Step5；

Step5：依次对客户集合B中其他客户点进行Step2～Step4操作，直到所有客户点均被服务，

输出完整线路，输出初始解.

3.3 破坏和修复策略设计

3.3.1 破坏算子 破坏算子对当前解中的客户点做出部分移除处理，目的是为移除的客户在后续安排更合理的路线，本文选用了三种破坏算子.

（1） 随机破坏算子：随机破坏是最常用的破坏方法，表示在当前解中随机移除一定个数的客户点，这样的方法有助于增加搜索的多样性，不易陷入局部最优.随机破坏是在当前解的客户集B中随机删除q个客户点，产生一个缺少q个客户点的部分解决方案和q个后续待插入的零散客户.

（2） 相关破坏算子：相关破坏算子的基本思想是将某些特征相似的点删除，原因是具有相关性的客户点在空间上往往呈现聚集的状态，删除这类客户点可在尽量少破坏已经较合理的规划线路前提下探寻更优的解.设置了两种相关性删除：① 距离相关破坏算子：这种删除基于点与点之间距离相关性，首先根据删除数量q生成待删除客户的空集列表A，从当前解Scurr的客户点集中随机选择一个客户点i，将它放入删除列表A中，然后计算Scurr中剩余点和i的距离，选择最近的点依次移入删除列表A中，直到A中的数量达到q.算子的相关性函数R1为：R1=dij；② 时间相关破坏算子：这种算子的破坏基于时间窗的相关性，同距离相关破坏算子操作一致，不同之处在于基于时间窗的相关性函数R2为：R2=ETi-ETj+LTi-LTj.

（3） 汇集度破坏算子：汇集度破坏算子就是优先破坏当前解的路径中服务客户数较少的那些路径，目的在于尽量删除短路径，减少发车数量.首先判断所有路径服务客户数量，选择在服务客户数量最少的路径中随机删除客户点，重复判断过程和删除过程直到删除数量达到q.

3.3.2 修复算子 修复算子是将破坏过程移除的客户点以更优的方式插入到当前解中，本文选用三种修复算子.

（1） 贪婪修复算子：贪婪修复算子的基本思想指将被移除的客户点逐个以最小插入成本的方式插回到路径中，贪婪插入比较的成本是插入客户点后总配送成本的大小，避免了插入成本和总配送成本变化不一致的情况.假设L表示所有可插入的路径的集合，L包括已发出车辆所在的路径和配送中心待发出车辆的路径，算子的核心思想就是找到使插入成本达到最小的路径和位置，然后将客户插入该位置.

（2） 最短距离修复算子：最短距离修复算子是根据客户点距离成本的大小来进行插入的，因为运输成本在成本内占比往往较高，所以以距离成本最小为插入的衡量标准有更高的概率找到最优方案.在每次迭代中，计算待插入客户点与路径中所有客户点的距离，选取距离最短路径及位置插入.

（3） 汇集度修复算子：汇集度修复算子的目的在于尽量少产生新的路径，减少发车数量.首先判断是否存在满足配送要求的已出发路径，如果存在按最小成本插入路径，如果不存在，选择距离客户点最近配送中心新派车配送.

3.4 算子选择策略和自适应权重调整机制

算子选择策略为赋予算子不同的权重值，通过算子权重的变化改变算子被选择的概率大小.本文算法在初始化阶段给予每个算子相同的权重值1，后期算子权重的调整有赖于算法自适应的过程，自适应过程其实就是计算并记录每个算子在迭代过程中的得分，用得分衡量该算子的表现，算子的表现越好得分越高，得分越高则在下一轮被选择的概率越大.预先为算法设置三种打分的分数σ1、σ2、σ3（σ1>σ2>σ3），算法根据新解可能出现的三种情况进行迭代过程中算子的评分过程：（1） 新解是一个新的全局最优解，评分增加σ1； （2）  新解优于当前解，评分增加σ2； （3）  新解差于当前解但仍被算法的接受准则接纳，评分增加σ3.对于某一个算子k而言，假设mk为在该片段中使用算子k的次数，πk为算子在该片段的得分，更新权重ρk如下式：

ρk=ρk， mk=0

ρk（1-ζ）+ρkπkmk， mk>0（36）

式中，ζ用于调整权重对于算子有效性的影响，取值在（0，1）之间.当ζ=0时，评分对权重无影响，当ζ=1时，权重的取值完全由评分决定.当0<ζ<1时，权重的取值同时考虑最近得分与过去的表现.

3.5 客户移除数量选择机制和终止条件

在每次进行破坏算子操作时都要明确需要移除的客户数量q，参考算子选择策略和自适应权重调整机制的评分过程，在每次破坏和修复操作前对移除客户数量q进行评分，设置了三种移除数量比例参数的选择q1、q2、q3，移除客户点的具体数量根据算例节点规模不同而变化.当算例中客户的数量为U时，假设此时选中的客户移除数量比例参数为q1，则实际移除的客户数量q为：q=Uq1.给三种移除数量比例参数每种一个初始权重1，后期权重根据移除数量参数的表现而变化.首先随机选择一种移除数量比例参数，每段迭代结束后会给该移除数量比例参数打分并根据分数修改该移除数量比例参数的权重，采用和破坏、修复算子一致的三种评分的分数σ1、σ2、σ3（σ1>σ2>σ3），算法依然根据新解可能出现的三种情况进行迭代中移除数量的评分过程.采用迭代次数终止规则，此规则通过设定最大迭代次数，一旦算法迭代搜索次数达到最大迭代次数则终止运行.

4 算例试验与结果分析

通过使用三种不同规模的数据对构建模型和提出的算法进行有效性测试，同时对算例结果进行分析，全部测试是在运行环境为2.4 GHZ Intel COREi5 CPU、内存4 GB的Windows10系统的Dell电脑上进行的，编程和运行软件为MATLAB R2018a.

4.1 算法参数分析

选择合适的评分机制更有助于算法整体效果的提升，因此对算法评分参数σ1、σ2、σ3、ζ进行分析，通过文献［10］找到五组已被验证有良好效果的评分机制，筛选出适合的一组评分机制，为后续的算例结果分析提供依据.分别用五组评分机制测算本文的小规模算例和中规模算例，为了尽量减少误差对求解结果的影响，每个算例测试三次，用S表示小规模算例，用M表示中规模算例，S-1表示小规模第一次测试、M-1表示中规模第一次测试，其余同理.小规模、中规模算例的测试结果见表2.

通过算例测试发现，几组评分分数在测试小规模算例时得到的结果相差不大，但是当测试中规模算例时差距开始显现，其中［1，0.4，0.25，0.25］这组分数的表现优于其余几组评分分数，更适合所研究的问题，因此选择这组参数进行后续的数据分析，客户数量移除比例参数通过测试调整得到，q1、q2、q3分别为1%、15%、30%.

4.2 算例求解与分析

文献［20］等采取了Solomon数据集中R102数据，但算例没有区分动态和静态客户.本文在其算例基础上进行改造，将算例中的客户分成静

态客户和动态客户，其中，小规模算例的客户点相关信息如表3所示，算例其他相关参数如表4所示，中、大规模算例客户点数据来源自文献［21］.将划分的时间片段即配送的时间间隔设置为1小时，客户满意度最小值为0.7，9∶00后开始处理［8∶00～9∶00］之间出现的动态客户信息.①②表示配送中心编号，1～5表示静态客户编号，6、7表示动态客户编号.

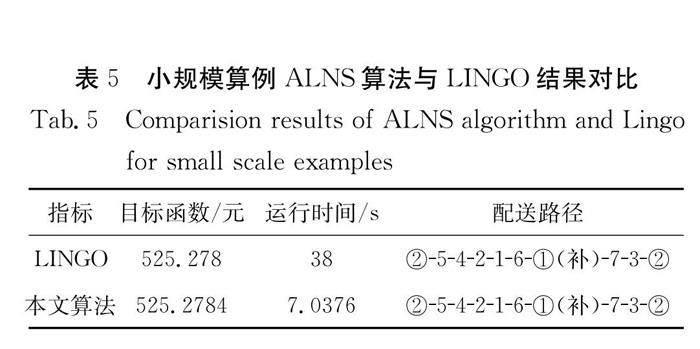
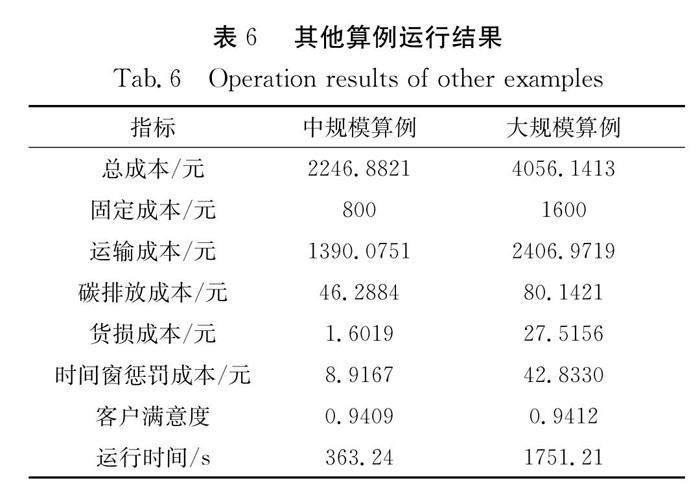
使用LINGO求解器求解小规模算例，验证模型的准确性，并和本文设计的ALNS算法求解结果进行对比，如表5所示. ALNS算法获得了和LINGO相同的最优解，而求解时间明显少于LINGO的求解时间.中规模算例有52个点，其中2个为配送中心点，30个静态客户点，20个动态客户点.编号1～30为静态客户，编号31～50为动态客户，动态更新4次，迭代次数设置为200次.大规模算例有103个节点，其中3个为配送中心点，60个静态客户点，40个动态客户点.编号1～60为静态客户，编号61～100为动态客户，动态更新6次，迭代次数设置为200次.两种规模运行结果如表6所示.静态客户的初始配送路径和动态结束后最终配送路径如表7所示.其中①（补）、②（补）、③（补）表示车辆去到某个配送中心补货.

由表6可以看出，中规模算例的总成本为2246.8821元，客户满意度的平均值0.9409，计算运行时间为363.24 s；大规模算例的总成本为4056.1413元，客户满意度的平均值为0.9412，计算运行时间为1751.21 s.可以发现，随着节点规模增大，更新次数增加，更新算法搜索范围变大，求得最优解的速度变缓，计算运行时间增加，但在可接受范围内.

4.3 对比分析

为了体现考虑动态需求的多配送中心沿途补货的冷链物流配送方案的优越性，将本文的方案与不允许沿途补货的考虑动态需求的多配送中心物流配送方案进行对比.由于不允许车辆沿途补货，当车辆服务下一个客户i的载重不足时，客户i的需求只能由路径中其他负载充足且满足所有约束条件的车辆服务或配送中心新派出车辆服务.选择中规模算例作为对比数据观察其对比效果，考虑沿途补货的配送方案和不考虑沿途补货的配送方案运行成本如表8所示.

由表8可以看出，相同客户规模下，不考虑沿途补货策略的配送方案对客户服务的成本要高于考虑沿途补货策略为客户服务的成本，高出了23.06%.同时，在客户满意度上，不考虑沿途补货策略配送模式的客户满意度也比考虑沿途补货策略配送模式的客户满意度要低8.69%.造成不考虑沿途补货策略成本高的主要原因是发车数量增加，虽然配送中心发出了更多的车辆为客户服务，但是客户的满意度没有因此提高，反而低于考虑沿途补货配送方案的客户满意度.

以上结果说明了考虑沿途补货策略的配送方案具有一定的优越性.本文的配送方案可以减少发车数量、减少企业的配送成本，同时不会牺牲客户的满意程度.

4.4 灵敏度分析

4.4.1 动态更新时间的灵敏度分析 对于动态需求配送模型来说，动态更新时间决定了配送的及时性，动态更新时间的长短极大地影响了车辆对动态客户服务的时间和路径安排，也会改变路径最终的配送成本.选择对更新次数较多的大规模算例进行测试，设置了四种更新时间，并对四种更新时间造成的配送成本变化和运行时间变化做出对比分析.更新时间及运行结果如表9所示.

由表9可知，随着动态更新次数的增加，配送的总成本逐渐增加，动态更新次数增加后算法的计算运行时间也增加了.这是因为更新时间间隔缩短时，系统更新路线的次数增加，动态客户大部分都能得到及时响应，无需积累到一定数量后才被处理，系统路线重叠次数增加，运输成本提高明显，因此总成本增加，算法计算时间也随之增加.虽然动态更新时间间隔缩短导致成本增加，但是客户的平均满意度却随着动态更新次数的增加而增加.这是因为动态客户需求得到及时响应，客户的等待时间变短，因此满意度提高.冷链物流企业可以根据自己的实际需求，衡量客户满意度和成本对自身企业的影响，动态调整更新时间间隔以达到利益最大化.

4.4.2 动态客户数的灵敏度分析 动态客户的数量对动态需求配送存在较大的影响.此处主要分析动态客户数量对配送路径的影响.采用动态度来表示动态客户的数量.动态度的表示方法为动态客户的数量除以全部客户数.动态客户数量越多，动态度越大.选择对中规模算例进行操作.中规模算例共20个动态客户，30个静态客户，因此动态度为0.4.改变中规模算例中的动态客户数量，对不同动态度的算例进行求解，运行结果如表10所示.

由表10可知，随着动态客户数量增加，路径的总配送成本增大.这是因为动态客户增多，路径的重新规划次数增多.除此之外，动态客户数量的增加也会使车辆的补货次数或新发车次数增加.因此配送的总成本不可避免的增大.同时，动态客户数量增加时，算法的计算运行时间也随之增加.这是因为在动态客户较少时，路径中的大部分客户为静态客户，在动态更新之前已经找到了较好的路径方案.因此少量动态客户重新加入路径时路径的改动相对较少，而动态客户数量很多时，路径的更新次数频繁，需要更久的计算时间才能实现路径的重新规划.

5 结 论

本文考虑动态客户需求和沿途补货的多配送中心冷链物流配送模型，更能满足当今市场客户对冷链配送更快速更准时的需求.采用主目标法对多目标问题进行处理转化为单目标问题，保证客户的满意程度在较高的范围内而不是一味追求成本低，这样更有助于企业的长期发展，增加企业的竞争力.

设计的自适应大邻域搜索算法可求解所构建模型，自适应评分机制可提高算法对本文问题的求解能力.通过小、中、大三种规模算例验证了本文算法的有效性.以中规模算例为例对比分析考虑沿途补货策略的和不考虑沿途补货策略的两种配送方案，发现考虑沿途补货策略后配送总成本可减少23.06%，发车数量减少3辆，满意度提高8.69%.这说明动态需求条件下考虑沿途补货策略的方案具有突出的优势.对动态更新时间间隔和动态客户数量的灵敏度分析结果表明：所有客户为完全动态客户时的配送成本要比所有客户为纯静态客户时的配送成本高出约65.14%，算法计算运行时间多出约66.28%；当动态更新时间间隔缩短时，动态更新次数增加，配送总成本增加，计算时间增加；当动态客户数量增加时，路径的总配送成本增大，计算时间增加.

未来此类问题仍需进行更深层次的研究，如适用场景变化，多分布不同数据集的测试，算法稳定性分析，多种车型共同配送等情况.

参考文献：

［1］ Cimen M， Soysal M. Time-dependent green vehicle routing problem with stochastic vehicle speeds： an approximate dynamic programming algorithm［J］. Transport Res D-Tr， 2017， 54： 82.

［2］ 王淑云， 孙虹， 牟进进. 随机需求下蓄冷式多温共配优化模型［J］. 系统管理学报， 2018， 27： 712.

［3］ Goel R， Maini R， Bansal S. Vehicle routing problem with time windows having stochasticcustomers demands and stochastic service times： Modelling and Solution ［J］. J Comput Sci-Neth， 2019， 34： 1.

［4］ Talouki R Z， Javadian N， Movahedi M M. Optimization and incorporating of green traffic for dynamic vehicle routing problem with perishable products［J］. Environ Sci Pollut R， 2021， 28： 36415.

［5］ 林明锦， 王建新， 王超. 考虑动态度和时间窗的两级车辆路径问题［J］. 计算机集成制造系统， 2021， 25： 1870.

［6］ 李延晖， 刘向. 沿途补货的多车场开放式车辆路径问题及蚁群算法［J］. 计算机集成制造系统， 2008， 14： 557.

［7］ 张景玲， 王万良， 赵燕伟. 基于沿途补货的多配送中心动态需求VRP建模及优化［J］.计算机集成制造系统， 2013， 19： 869.

［8］ Luca B， Nicola S. Faster rollout search for the vehicle routing problem with stochastic demands and restocking ［J］.Eur J Oper Res， 2018， 270： 1.

［9］ 李国明， 李军华. 基于混合禁忌搜索算法的随机车辆路径问题［J］. 控制与决策， 2021， 36： 2161.

［10］ Lahyani R， Gouguenheim A L， Coelho L C. A hybrid adaptive large neighbourhood search for multi-depot open vehicle routing problems ［J］. Int J Prod Res， 2019， 57： 6963.

［11］ Husakou A， Hvattum L M， Danielsen K， et al. An application of the multi-depot heterogeneous fixed fleet open vehicle routing problem ［J］. Int J Adv Oper Manag， 2020， 12： 142.

［12］ Sadati M， Atay B. A hybrid variable neighborhood search approach for the multi-depot green vehicle routing problem ［J］. Transport Res E-Log， 2021， 149： 102293.

［13］ 范厚明， 张轩， 任晓雪， 等. 多中心开放且需求可拆分的VRPSDP问题优化［J］. 系统工程理论与实践， 2021， 41： 1521.

［14］ 张冬青， 郭钊侠， 张殷杰.考虑时空相关随机行驶时间的车辆路径问题模型与算法［J］. 四川大学学报： 自然科学版， 2021， 58： 067001.

［15］ 刘志硕， 李秋雨， 董子琦， 等. 带软时间窗的冷链电动车辆路径问题研究［J］. 北京交通大学学报， 2022， 46： 57.

［16］ 安健. 基于ALNS算法的城市商品配送车辆路径问题研究［D］. 南京： 南京大学， 2020.

［17］ Ropke S， Pisinger D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows［J］. Transport Sci， 2006， 40： 1.

［18］ 李荡. 时变路网条件下模糊需求车辆路径优化研究［D］. 大连： 大连海事大学， 2020.

［19］ 南丽君， 陈彦如， 张宗成. 改进的自适应大规模邻域搜索算法求解动态需求的混合车辆路径问题［J］. 计算机应用研究， 2021， 38： 2926.

［20］ 王宁， 胡大伟， 徐杰， 等. 基于客户价值和满意度的城市冷链物流时变路径问题［J］. 中国公路学报， 2021， 34： 297.

［21］ 段诗远. 考虑碳交易的生鲜农产品冷链配送选址-路径研究［D］.北京： 北京交通大学， 2019.