基于模糊调参规则和IDOB 的光电平台复合控制方法
何锦廷, 谷 奇, 丁祝顺, 孙 寅, 张明闯
(1. 北京航天控制仪器研究所, 北京 100039;2. 北景国测(上海)量子科技有限公司, 上海 201306)
0 引言
航空光电平台由机械结构和伺服控制系统组成, 为光电吊舱在惯性坐标系下提供高精度的视轴稳定功能[1]。 当载体平台高速、 大机动运动时,光电平台因受到外部机体的随机振动与气流颤振等影响, 造成光学载荷视轴抖动、 成像模糊失真等现象[2], 对目标探测识别距离、 目标定位精度等功能带来不利影响, 严重时甚至导致光轴偏离目标[3], 跟踪功能失效。 因此, 在这种多变复杂的动态环境下, 有效补偿扰动对提升光电平台性能具有重要意义。
对于光电平台而言, 控制系统的外部扰动具有时变性, 并且不平衡扰动力矩、 线束干扰力矩、耦合力矩等不易精确建模, 传统PID 也因参数固定而不能适应系统的变化, 因此需要扰动观测器或其他算法加以优化。 陈晓刚等[4]为了补偿摩擦、 线缆弹性力矩以及风阻力矩等干扰, 建立了Stribeck摩擦模型, 并进行了扰动观测器反馈补偿, 所提算法比传统PID 具有更小的位置跟踪误差。 DENG等[5-6]设计了双补偿扰动观测器对干扰进行估计,与标准DOBC 方法相比, 双补偿扰动观测器具有叠加的干扰抑制功能, 在不改变稳定裕度和跟踪能力的情况下, 可以抑制更多的干扰; TONG 等[7]、LU 等[8]提出了有参数自整定能力的模糊控制算法,其抗干扰能力和跟踪能力明显优于传统PID 控制器。 但在工程实验中, 模糊PID 控制因受系统机械谐振的限制, 仅在一定范围内提高了系统带宽,对扰动的补偿具有局限性。
在上述研究的基础上, 本文建立了光电平台动力学模型。 考虑轴端摩擦力对稳定平台动力学响应的影响, 构建了LuGre 摩擦模型和控制系统回路模型, 提出了模糊算法与改进干扰观测器(Improved Disturbance Observer, IDOB) 组合的控制方法。 结合航空光电平台的实际工况, 对本文所提的基于复合控制系统的稳定性进行仿真分析和实验验证。
1 光电平台建模
1.1 两轴平台模型
(1)平台动力学建模
航空光电平台属于伺服控制系统, 以两轴两框架平台系统为例, 其结构示意图如图1 所示。

图1 两轴光电平台结构示意图Fig.1 Structure diagram of two-axis photoelectric platform
光电平台基座、 方位框架和俯仰框架坐标系示意图如图2 所示。 其中, 光电平台基座坐标系为R系, 方位框架坐标系为A系, 俯仰框架坐标系为P系。 由于光电平台基座与载体固连, 因此光电平台基座坐标系与载体坐标系的方向一致。
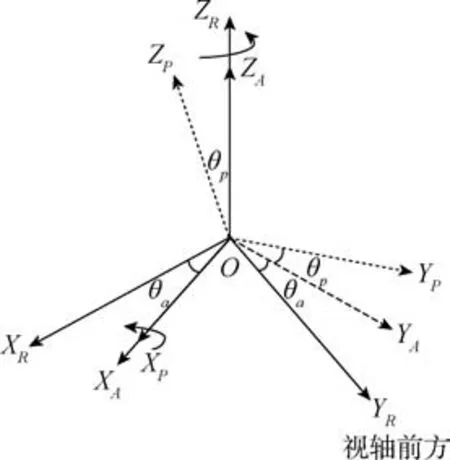
图2 光电平台基座、 方位框架和俯仰框架坐标系示意图Fig.2 Schematic diagram of coordinate systems for photoelectric platform base, azimuth frame and pitch frame
假定框架结构为刚体, 且沿俯仰轴存在非对称分布质量, 根据欧拉运动学方程, 可建立俯仰框架的动力学方程为[9]
式(1)中,HP和JP为俯仰框架的惯性角动量和惯性张量。 由式(1)可得, 俯仰轴直流力矩电机绕定轴转动的动力学力矩TPx为
式(2) 中,Ixx为俯仰框架绕x轴的转动惯量,ωP=[ωPxωPyωPz]为俯仰框架在惯性空间的角速度,TPe为动态非平衡惯量产生的干扰力矩,TPd为俯仰框架与方位框架相对运动产生的耦合力矩。当俯仰框架保持某个角度θp时, 同理, 方位轴直流力矩电机绕定轴转动的惯性角动量HA和动力学力矩TAz可表示为
式(3)中,HA和JA为方位框架的惯性角动量和惯性张量,为俯仰框架到方位框架的旋转变换矩阵,IAz为方位框架绕z轴的转动惯量,ωA=[ωAxωAyωAz]为方位框架在惯性空间的角速度,TAe为动态非平衡惯量产生的干扰力矩,TAd为两框架相对运动产生的耦合力矩。
(2)摩擦力模型
摩擦力模型选择广泛使用的LuGre 摩擦模型[10], 表达式如下
式(4)中,F为摩擦力矩估算值,v为接触面的相对速度,z为鬃毛的平均形变,σ0为鬃毛刚度,σ1为微观阻尼系数,σ2为黏性摩擦因数,Fs为最大静摩擦转矩,Fc为库伦摩擦转矩,vs为Stribeck速度, 指数α取0.5。
1.2 控制系统回路
由于光电平台俯仰框架和方位框架的驱动方式、 控制方法及扰动作用原理类似, 因此本文选择俯仰框架作为研究对象。 俯仰框架伺服系统采用两环控制, 如图3 所示, 内环为电流环, 外环为速率环。 内环决定了系统的响应速度和电机的抗干扰能力, 外环主要降低外界扰动对光电平台伺服系统稳定性的影响。 本文将电流环已调节至最佳带宽并保持不变, 重点对速率环进行分析研究。
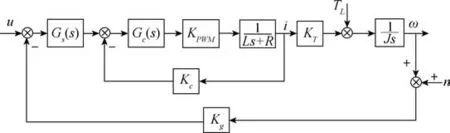
图3 控制系统回路框图Fig.3 Block diagram of control system loop
图3 中,u和ω为系统的输入和输出,Gs(s)为速率环的控制器,Gc(s) 为电流环的控制器,KPWM为PWM 的增益系数,为电机简化模型,i为电机电枢电流,Kc为电流检测反馈系数,KT为力矩系数,TL为控制系统干扰,J为折算到电机轴上的转动惯量,Kg为陀螺增益,n为测量噪声。
2 控制器设计
光电平台伺服系统控制器分为两部分设计:1)由于伺服控制系统中存在质心分布不均匀、 俯仰角变化及电机磁场气隙随时间变化等影响因素,使得光电平台系统的转动惯量和电机力矩系数等参数是时变的, 为此采用了模糊控制, 以提高控制系统的鲁棒性; 2)针对轴端摩擦和一些难以精确建模的未知干扰, 通过干扰观测器(Disturbance Observer, DOB)观测相应的状态量并进行实时补偿。但由于传统DOB 包含微分环节, 高频测量噪声难以消除, 影响了光电平台视轴稳定精度, 因而提出IDOB, 将所观测的扰动通过等效控制量的方式进行反馈补偿。
2.1 模糊PID 控制器设计
模糊PID 控制采用模糊规则和模糊集合进行推理判断, 以偏差e和偏差变化率ec为输入, 偏差变化率采用一阶后向差分法, 通过不断迭代检测e和ec, 对PID 参数进行在线修改, 在实际应用中具有一定的自适应性、 容错性和鲁棒性[7]。 光电平台模糊PID 控制器公式为
式(5) 中, Δkp、 Δki为模糊控制器输出的比例、 积分系数的实时增量。
根据稳定效果进行多次仿真分析后[7], 确定输入e、ec的模糊论域均为[ -6, 6], 量化因子为5和0.03; 输出模糊语言变量Δkp、 Δki的模糊论域均为[0, 6], 量化因子为0.005 和0.25。 将输入变量e、ec和输出变量Δkp、 Δki的模糊集均设定为{NB, NM, NS, ZO, PS, PM, PB}; 模糊输入、输出的隶属度函数均为三角分布函数。 模糊规则如表1、 表2 所示。
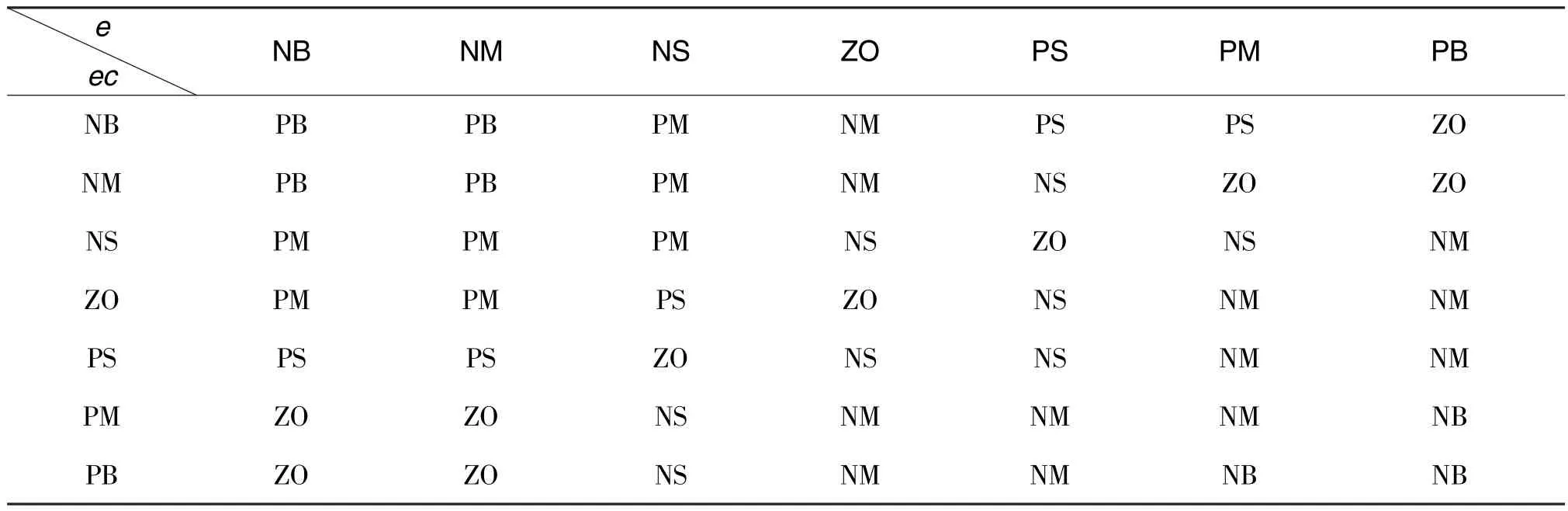
表1 Δkp 的模糊规则Table 1 Fuzzy rules of Δkp

表2 Δki 的模糊规则Table 2 Fuzzy rules of Δki
2.2 改进型观测器设计
传统DOB 是通过建立标称模型代替实际被控对象, 并将观测的干扰值进行反馈, 与控制器共同输出带有抵消扰动的控制量, 从而达到消除干扰的目的。 基于传统DOB 的结构应用到光电平台系统中, 其结构框图如图4 所示。
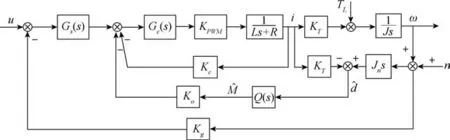
图4 传统DOB 系统的结构框图Fig.4 Structure diagram of traditional DOB system
图4 中,Jn与转动惯量J相等,Q(s)为低通滤波器,Ko为传统DOB 的反馈系数,为对干扰力矩的估计,为传统DOB 的输出, 仿真时测量噪声n是从陀螺手册中获取。 由图4 可知, 伺服系统输出ω为
式(6)中,G′c(s)为电流环闭环传递函数。 传统DOB 输出为
由式(6)可知, 当高频段Q(s) =0 时, 系统对测量噪声不敏感; 当低频段时,系统可以补偿低频的扰动。 由于被控对象的相对阶次不为0, 其逆含有微分算子, 且微分算子因需要未来时刻的输入信息在物理上难以实现, 并且会导致系统对高阶测量噪声敏感, 为此对传统DOB 提出如下改进:
与传统观测器不同的是: 在传统DOB 补偿扰动思想的基础上, 将式(7)的一阶微分算子s利用一阶低通滤波器构成的回路近似代替, 可得对扰动估计的量
从式(8)中可看出其不含微分环节, 在工程上具有可行性和简洁性。 基于IDOB 的光电平台控制结构如图5 所示。
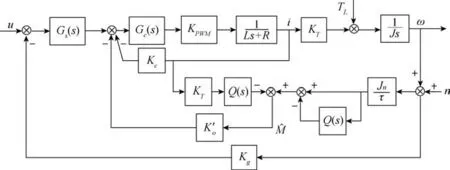
图5 基于IDOB 的系统控制结构图Fig.5 System control structure diagram based on IDOB
图5 中,K′o为改进干扰观测器(IDOB)的反馈系数,τ为时间常数。
改进后的伺服系统输出如下
本文所设计的控制器采用了模糊控制与IDOB反馈补偿相结合的控制策略, 通过模糊算法在线修改PID 参数的方式形成模糊PI 控制器(模糊PID控制器D 参数为0), 替代了速率环控制器Gs(s),再结合IDOB 估计的扰动值, 形成对外界扰动的控制量。 基于复合控制方法的光电平台伺服系统总体框图如图6 所示。

图6 复合控制系统总体框图Fig.6 General block diagram of composite control system
3 仿真分析与实验
3.1 仿真分析
IDOB 的关键是设计合适的时间常数τ, 而τ的选择需要在对干扰的抑制能力和对噪声的敏感度之间权衡, 时间常数越小, 对低频干扰的抑制能力越强, 但同时对高频噪声也越敏感, 反之则情况相反[11]。 取τ分别为0.001、 0.01、 0.05 和0.1 时, 基于不同时间常数的IDOB, 对干扰的估计效果如图7(a) 所示, 对干扰的补偿效果如图7(b)所示。 图7 中的曲线a1、a2、a3、a4分别对应的是τ取0.1、 0.05、 0.01、 0.001。
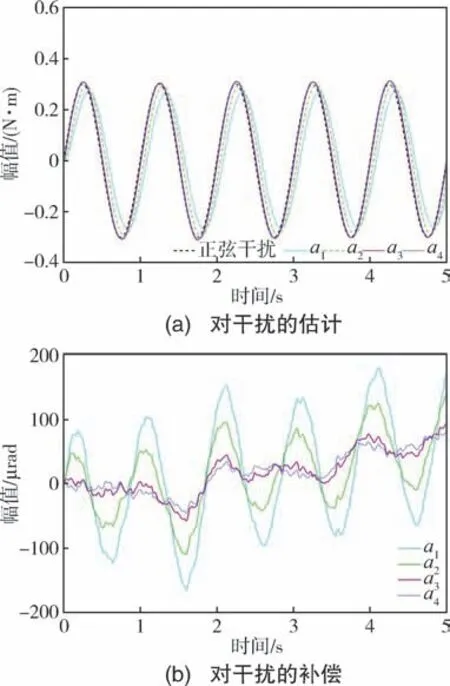
图7 基于不同时间常数的IDOB 对干扰的观测及补偿效果Fig.7 Observation and compensation effects of disturbance based on IDOB with different time constants
由图7(a)可知, 时间常数τ取0.001 和0.01时对干扰的估计延迟不大, 分别为0.005 s 和0.011 s; 而τ取0.05 和0.1 时, 时间延迟分别为0.048 s 和0.085 s。 由图7(b)可知,τ取0.01 时相比τ取0.001 时对干扰的补偿效果最大差10.07 μrad;而τ取0.05、 0.1 时相比τ取0.001 时对干扰的补偿效果最大分别差59.53 μrad、71.62 μrad。 但由于τ取太小时IDOB 的带宽过大,高频噪声难以抑制, 因此综合考虑选取τ=0.01。
为了验证模糊PID 控制和IDOB 方法的有效性和可行性, 对其分别进行Matlab/Simulink 仿真分析。 由于光电平台系统中的转动惯量和力矩系数等参数是时变的, 为此进行了参数变化±10%和模型参数为平均值两种情况的仿真。
(1)模型参数变化±10%
当模型参数转动惯量、 力矩系数不固定时,在1 Hz 和5 Hz 的正弦干扰条件下, 基于模糊PID控制的系统动态误差峰值如表3 所示。

表3 模型参数变化±10%时的基于模糊PID 控制的系统动态误差峰值Table 3 Peak value of system dynamic error based on fuzzy PID control when model parameters change ±10%
由表3 可知, 当光电平台系统参数变化±10%时, 在正弦干扰频率为1 Hz 条件下采用模糊控制的系统动态误差峰值相差较小, 表明基于模糊PID的控制系统具有一定的鲁棒性。 而干扰频率变为高频时, 系统动态误差峰值相差较大, 模糊算法的鲁棒性降低。
(2)模型参数为平均值
光电平台伺服稳定控制系统转动惯量、 轴端摩擦系数等主要参数如表4 所示。

表4 光电平台伺服稳定控制系统主要参数Table 4 Main parameters of servo stabilizing control system for photoelectric platform
为了验证IDOB 对干扰估计的准确性, 分别给系统施加一个角速度峰值为1 (°) /s、 频率为1 Hz和5 Hz 的干扰运动, 并由LuGre 摩擦模型产生相应的摩擦力矩, 通过IDOB 得到的扰动估计值如图8 所示。
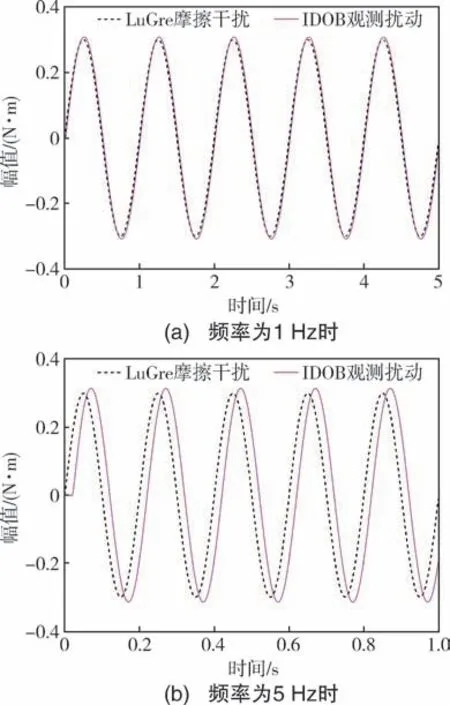
图8 IDOB 对正弦干扰的估计Fig.8 Estimation of sinusoidal disturbance by IDOB
由图8 的仿真结果可知, 在正弦干扰运动频率为1 Hz 时, IDOB 对扰动的观测值与实际值间的差值为0.0078 N·m, 表明IDOB 对扰动具有较好的估计效果。 但当正弦干扰运动频率为5 Hz 时,IDOB 对扰动的估计准确性降低。
设置参考输入u=0、 正弦干扰力矩输入TL=0.02sin2πft(f=1 Hz、f=5 Hz)。 通过系统仿真,可得到传统PID 和IDOB 控制策略的动态误差对比, 如图9 所示。
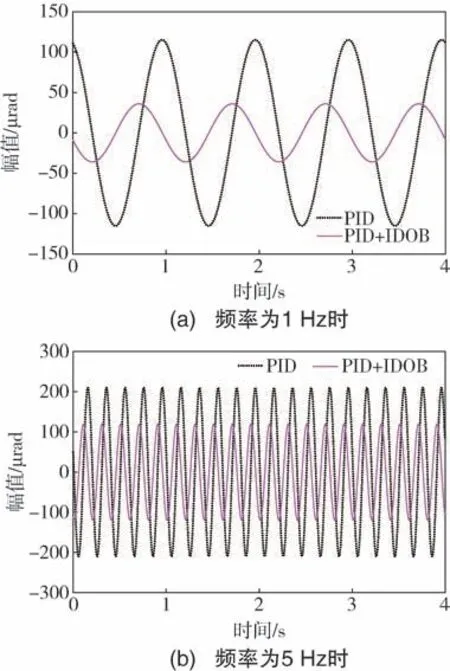
图9 正弦干扰运动频率为1 Hz 和5 Hz 时两种方法的动态误差对比Fig.9 Dynamic error comparison of two methods when sinusoidal disturbance motion frequency is 1 Hz and 5 Hz
由图9 的仿真结果可知, 在1 Hz 正弦干扰条件下, 传统PID 控制器会因超调量、 带宽以及稳态时间等动态性能的约束, 对扰动补偿的能力达到了极限, 系统输出的动态误差峰值为115.2 μrad,超出了稳定精度为100 μrad 的指标要求。 而IDOB输出的动态误差峰值为35.92 μrad, 在指标要求之内, 且由式(9)算出的动态误差峰值为46.6 μrad,理论与仿真分析结果相近。 但当频率为5 Hz 时,本文方法对扰动的补偿效果降低。
3.2 实验测试
为了测试本文复合算法对扰动的抑制效果,将光电平台安装在双轴摇摆台上, 并设置正弦摇摆幅值为1°、 频率为0.5 Hz ~2 Hz, 如图10 所示。陀螺采用的是ADIS16460, 采样频率为500 Hz。 控制软件是基于keil uVision5 软件编写。 令光电平台处于惯性稳定状态, 通过获得平台伺服系统输出的陀螺信号来分析对扰动的补偿效果。 图11 为在双轴摇摆台上通过IDOB 观测到的扰动曲线。

图10 双轴摇摆台实验Fig.10 Experiment of two-axis swing table
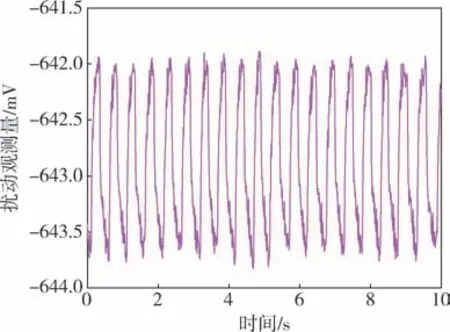
图11 IDOB 观测到的扰动曲线Fig.11 Disturbance curve observed by IDOB
通过正弦摇摆实验, 获得俯仰轴陀螺在干扰频率为2 Hz 时的输出情况, 如图12 所示。 基于模糊PID 和复合控制两种方法的光电平台系统在0.5 Hz ~2 Hz 干扰频率下的RMS 值如表5 所示。
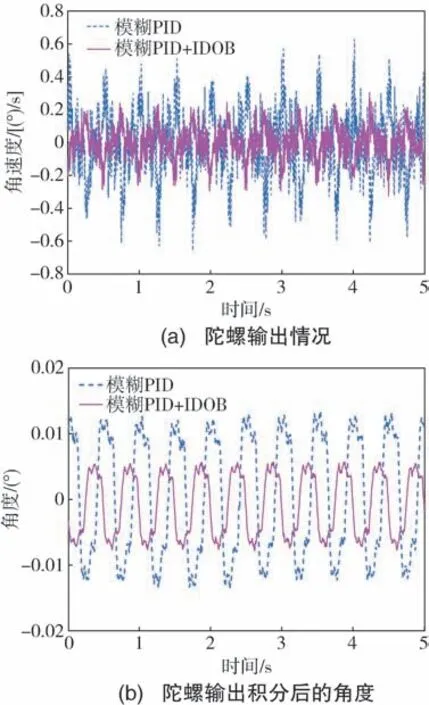
图12 两种方法在干扰频率为2 Hz 时的俯仰轴陀螺输出及积分后的角度Fig.12 Pitch axis gyro output and angle after integration for two methods when the disturbance is 2 Hz
由表5 可知, 经实验数据处理后, 随着正弦干扰频率的增加, 基于模糊PID 和复合控制方法的控制系统稳定性逐渐变差, 但基于复合控制方法的光电平台系统在频率为2 Hz、 幅值为1°的正弦扰动条件下的RMS 值, 相比模糊PID 控制的RMS 值减小了12.24%。 由此可见, 本文提出的复合控制方法能够有效提高光电平台的稳定性。
4 结论
为了解决光电平台轴端摩擦等干扰影响平台系统视轴精度的问题, 提出了一种基于模糊算法与IDOB 的光电平台复合控制方法, 即解决了在工程上控制系统易受时变低频扰动影响的问题, 又可避免传统DOB 在物理上难以实现的不足。 实验结果表明, 在低频干扰运动下, 基于模糊控制与IDOB复合控制的伺服系统, 具有较好的稳定性和鲁棒性,对工程实践具有参考意义。 但当干扰频率为高频时,本文复合控制方法应用效果不理想, 可通过加入模型预测控制进一步提高系统估计的带宽。

