改进的自适应最大相关熵UKF 算法在SINS/GNSS 组合导航中的应用
黄海舟, 周凌柯, 张永耀, 蔡紫烨, 李 胜
(南京理工大学自动化学院, 南京 210094)
0 引言
捷联惯性导航系统(Strapdown Inertial Navigation System, SINS)和全球导航卫星系统(Global Navigation Satellite Systems, GNSS) 在导航任务中应用广泛, SINS 具有长期稳定性差、 短期稳定性好、 动态性能好的特点, 而GNSS 则正好相反, 因此工程上常将两者通过组合导航技术结合起来, 组成SINS/GNSS 组合导航系统, 以提升组合导航的整体性能[1]。 SINS/GNSS 组合导航系统是典型的非线性系统, 无论是导航参数解算还是导航方程建立都涉及非线性问题, 且系统中的噪声多为非高斯噪声[2]。 当前, 扩展卡尔曼滤波(Extended Kalman Filter, EKF)被广泛应用于组合导航系统设计, 然而当系统模型的非线性较强时, EKF 滤波精度会严重下降甚至发散, 鲁棒性较差[3]。
为了克服EKF 存在的问题, 有学者提出了无迹卡尔曼滤波(Unscented Kalmam Filter, UKF)。UKF 利用无迹变换对非线性系统的状态后验概率密度函数进行近似, 可以从二阶以上精度近似高斯线性系统的状态后验均值与方差。 此外, 相比于EKF, UKF 无需计算Jacobian 矩阵, 具有滤波精度高、 计算简单、 收敛性好等特点[4-5]。 然而,UKF 与EKF 均假设系统中噪声服从高斯分布, 当系统中噪声非高斯时, 会存在鲁棒性较差、 滤波精度下降的问题[6]。
文献[7]、 文献[8]提出了一种基于最大相关熵准则(Maximum Correntropy Criterion, MCC) 的卡尔曼滤波器(Kalman Filter, KF), 研究表明MCC-KF可以较好地应对非高斯噪声的影响, 滤波精度相比于传统KF 有较大提升。 文献[9]研究了一种鲁棒的MCC-UKF 算法, 将MCC 与UKF 结合, 提高了算法的滤波精度和鲁棒性。 文献[10]研究了核宽对MCC 算法迭代性能的影响并得出了结论:在一定范围内, 较大核宽能够加快算法收敛速度, 但会导致稳态误差变大; 较小核宽收敛速度较慢, 但稳态误差较小。 文献[11] ~文献[13] 研究了几种不同的核宽自适应准则, 结果表明: 相比于定核宽, 变核宽能在一定程度上提高算法的精度, 但是部分结果显示应对强脉冲噪声时的稳定性较差。 文献[14] 提出了一种变量核宽MCC,通过改写代价函数, 解决了强脉冲噪声条件下的稳定性问题, 然而这种方法提高了算法的复杂度。
本文针对传统MCC 算法受核宽大小影响的问题, 对基于传统MCC 的UKF 滤波算法进行了相关研究和改进。 利用改进的量测噪声自适应方法对量测噪声进行自适应调整, 并结合新的自适应核宽算法, 提出了自适应变核宽的ADMCC-UKF 算法。 通过SINS/GNSS 仿真实验, 验证了所提出的改进算法的有效性与优越性。
1 传统UKF 算法
考虑非线性离散系统, 其状态方程及量测方程如下
式(1)中,Xk∈Rn×1、Yk∈Rm×1分别为k时刻系统的状态向量和量测向量;f(·)为非线性状态转移函数; 系统噪声qk、 量测噪声rk为互不相关的零均值高斯白噪声序列, 其统计特性如下
式(2)中,Qk为非负定矩阵,Rk为正定矩阵,δkj为Kronecker 函数。
UKF 算法的基本过程如下:
(1)初始化
(2)计算sigma 点
(3)时间更新
(4)量测更新
2 改进的ADMCC-UKF 算法
传统MCC 算法利用核函数中核宽的设置, 在迭代中削弱了非高斯噪声的影响。 然而传统MCC算法中核宽常设置为定值, 不仅降低了算法的收敛速度, 而且往往无法获得好的稳态误差结果。本文设计了一种自适应核宽(Adaptive MCC, ADMCC)算法, 首先进行量测噪声估计, 通过噪声估计的变化程度确定核宽调整的上界和下界; 然后依据算法的迭代误差对核宽进行自适应调整, 大大提高了收敛速度。
2.1 核宽自适应算法设计
(1)最大相关熵准则
在信号处理领域, 常使用随机过程的统计分布和时间结构对信号进行描述和分析。 文献[16]基于核方法(Kernel Method)和信息理论学习(Information Theoretic Learning, ITL) 技术提出了相关熵的概念, 文献[17] 对相关熵进行了进一步补充和分析。
相关熵表示两个随机变量X和Y之间的相似程度, 其定义如下
式(15)中,pXY(x,y)为联合概率密度,κσ(x,y)为Mercer 核函数。 其中, 最常用的核函数为高斯核函数
式(16)中,e=x-y,σ为核宽(σ>0)。 在实际情况中,X和Y的概率密度函数通常难以获取,因此常使用样本的平均估计量来对相关熵Cσ(X,Y)进行估计
由式(15)、 式(16)可知, 高斯核下的相关熵非负, 且在x=y时相关熵取得最大值。 相关熵的实质是对两个随机变量之差高斯变换后的函数求取数学期望, 两个分布的相关熵越大, 说明两个分布越相似。 当噪声序列呈现非高斯分布时, 特别是出现脉冲分布时, 噪声序列大概率会出现大值偏差。 相比于最小均方误差准则, 此时高斯核中负指数项和设置的核宽σ共同作用, 削弱大值偏差对相关熵的影响, 所以在非高斯噪声环境下能取得更好的性能[18]。
(2)改进的ADMCC 算法
在MCC 算法迭代求解过程中, 初始迭代误差大小与量测噪声相关, 因此可以利用量测噪声的变化信息对核宽的变化范围进行界定。 本文利用Sage-Husa 自适应滤波的思想, 对当前时刻的量测噪声进行估计, 步骤如下:
传统Sage-Husa 自适应滤波认为量测噪声的方差是缓慢变化的, 该方法并不适用于方差快速变化或量测出现粗差的情形, 文献[19]对噪声自适应过程做了如下改进
式(20) 中,s为缩小因子, 一般取2 ~4。 由式(20)可知, 在高斯分布的范围内的量测噪声都视为正常噪声, 而不在此范围的量测噪声则视为粗差噪声。 当偏差严重时, 对应的量测方差将对应变大, 其对状态估计的影响会减小, 一定程度上提升了抗干扰能力。
利用式(19)、 式(20)能够确定改进的可变核宽σ(t)的变化区间为。 其中,σ0为初始核宽,k的取值如下
式(21)中,k为放大系数, 1 <k<σ0,mean(·)为平均值,Nw为窗口大小。 分析式(21) 可知, 当k≤1 时, 即当前时刻量测方差估计值小于历史时刻量测方差均值时, 此时的可变核宽σ(t) =σ0,退化为定核宽, 与传统MCC 一致, 可以认为此时不需要对核宽进行调整即可获得较好的性能, 有效减少了计算量; 当1 <k<σ0时, 即当前时刻量测方差估计值大于历史时刻量测方差均值时, 令可变核宽σ(t) 在初始核宽σ0的邻域和(σ0,kσ0]内变化, 保证了算法的鲁棒性。
当1 <k<σ0时, 本文利用高斯函数和迭代误差e(t)来调整核宽
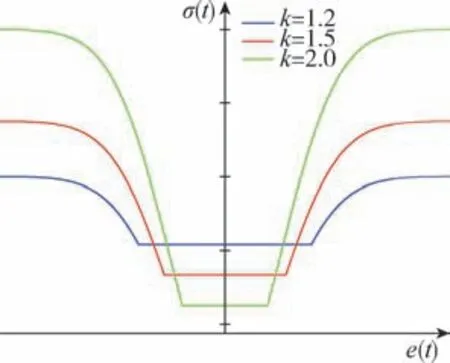
图1 不同k 值下核宽随迭代误差变化曲线Fig.1 Curves of kernel width variation with iteration error under different k values
分析图1 可知, 随着k值增大, 可变核宽σ(t)的变化范围越大, 核宽下界越窄, 有助于在迭代误差较小时获得更小的稳态误差; 随着k值减小,σ(t)的变化范围越小, 核宽下界越宽, 有助于提高系统收敛速度; 在同一迭代误差下, 量测噪声越大, 核宽越大, 量测对应权值越小, 有助于对当前的系统误差进行控制。
2.2 基于变核宽MCC 的量测更新重构
MCC 算法通过对卡尔曼滤波的量测更新部分进行重构, 获得一种基于MCC 的鲁棒滤波算法。本文将MCC 算法与提出的改进核宽自适应算法相结合, 得到一种改进的自适应MCC 鲁棒滤波算法。
利用状态预测误差与量测误差构造误差矩阵Ek
式(23)中,CP,k/k-1和CR,k为下三角矩阵, 分别由Pk/k-1和Rk通过Cholesky 分解得到[20]。
根据式(17) ~式(23), 结合本文提出的自适应核宽σ(t), 可以构造如下的代价函数
式(24)中,ei,k为Ek中的第i行元素,n为状态量维数,m为量测量维数。 通过式(24)构造的代价函数, 可以利用梯度下降法对状态变量Xk进行迭代求解, 求解过程如下:
对代价函数J(xk)求取关于Xk的偏导数, 可得
令式(25)为零并化简, 可得
式(26)中,
可以令
则式(26)可化简为
最后, 计算k时刻的状态预测误差
由预测误差更新Pk
2.3 ADMCC-UKF 算法流程
基于2.1 节、 2.2 节内容得到的自适应ADMCC-UKF 算法流程如下:
(1)初始化
(2)时间更新
(3)量测噪声自适应
根据式(18) ~式(20)计算k时刻的Rk。
(4)量测更新
②根据式(23)计算ei,k;
③根据式(21)、 式(22)计算迭代核宽σ(t);
④根据式(27) ~式(29)计算ΠP,k、ΠR,k、Πi,k;
⑦根据式(36)更新Pk。
3 实验及分析
本文利用SINS/GNSS 组合导航模型对所提算法性能进行仿真验证和实车验证, 在此直接给出SINS/GNSS 组合导航的数学模型。
3.1 SINS/GNSS 组合导航系统模型
(1)系统状态方程
选取地理坐标系即“东、 北、 天” 坐标系作为导航坐标系(n系), SINS 计算所得的导航坐标系为p系。 SINS 的姿态、 速度、 位置误差模型如下
设n系与p系的失准角为φ=[φxφyφz]T,则坐标变化矩阵为
(2)系统量测方程
利用GNSS 得到的三轴位置信息对SINS 进行定期滤波校正, 式中量测方程定义如下
式(40)中,O3×6为3 ×6 维零矩阵,I3×3为3 ×3 维单位矩阵。
3.2 仿真实验设计
本实验采用西北工业大学严恭敏团队开发的高精度惯性导航工具箱[21], 生成一组无人车轨迹数据以及对应的SINS 数据, 利用本文提出的ADMCC-UKF 算法, 与MCC-UKF 算法和传统UKF 算法进行比较, 从组合导航系统精度、 算法运行时间两方面验证本文算法的有效性。 实验参数设置如表1 所示。

表1 实验参数设置Table 1 Settings of experiment parameters
设置小车初始位置为东经108°、 北纬34°, 载体初始速度为0 m/s, 方向正北, 载体经过加速、匀速、 左转弯、 右转弯、 绕圈、 上坡、 下坡、 减速等机动过程, 行驶时长为950 s, 行驶轨迹如图2 所示, 红色标记处为小车的起始位置。

图2 载体行驶轨迹Fig.2 Diagram of carrier driving trajectory
为了验证改进算法对非高斯问题的有效性, 取载体行驶过程中的三个时段100 s ~200 s、 250 s ~350 s、 400 s ~500 s 添加受污染的高斯噪声, 混合比α=0.3。 混合高斯噪声分布如下
3.3 跑车实验设计
为了进一步验证算法的有效性, 使用实验室无人车采集了一组轨迹数据, 实验场地位于南京理工大学喷泉广场。 实验设备性能参数如表2 所示。

表2 实验设备性能参数Table 2 Performance parameters of experiment equipments
使用无人车的内置高精度RTK 采集一组轨迹,如图3 所示。 红色标记处为小车起始点, 小车逆时针行驶一圈后停止, 行驶时长约220 s。
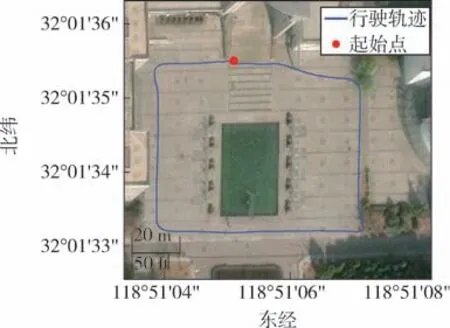
图3 无人车的行驶轨迹Fig.3 Diagram of unmanned vehicle driving trajectory
为了验证改进算法对非高斯问题的有效性,在GNSS 原始数据中随机添加10%如式(41)所示的混合高斯噪声, 以模拟GNSS 定位质量较差的场景。
3.4 实验结果及分析
采用蒙特卡罗仿真方法, 设置仿真次数M=50, 计算位置均方误差RMSEδp和平均位置均方误差ARMSEδp, 并对仿真结果进行对比。 计算公式如下
利用惯导工具箱生成的载体行驶轨迹数据,分别采用传统UKF 算法、 MCC-UKF 算法和本文所提的ADMCC-UKF 算法对SINS/GNSS 组合导航系统进行仿真, 结果如图4 ~图6 所示。 采用无人车行驶时采集的IMU、 GNSS 数据进行仿真, 结果如图7 ~图10 所示。 根据式(43)计算仿真实验和跑车实验的平均位置均方误差, 结果如表3、 表4 所示。 统计仿真实验中三种算法的运行时间, 结果如表5 所示。

表3 仿真实验的平均位置均方误差Table 3 ARMSE of simulation experiment
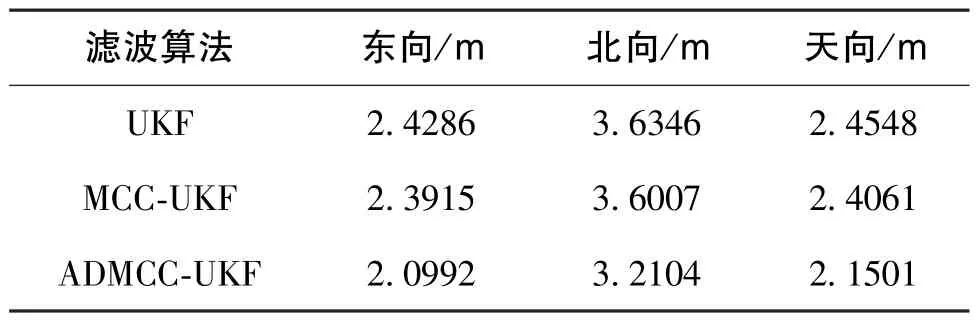
表4 跑车实验的平均位置均方误差Table 4 ARMSE of real vehicle experiment
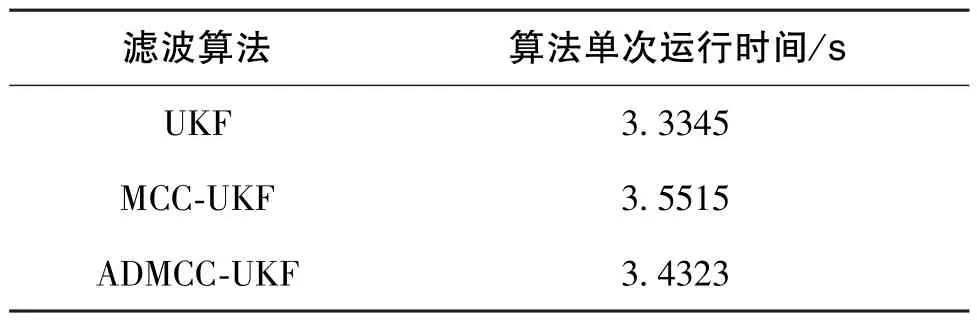
表5 算法单次运行时间Table 5 Single running time of the algorithm

图4 东向位置仿真的RMSEFig.4 RMSE of simulation for east position
由图4 ~图6 可知, 传统UKF 算法精度最差,本文提出的ADMCC-UKF 算法精度接近MCC-UKF算法, 能很好地减轻系统噪声统计特性变化带来的影响, 精度均优于UKF 算法。 UKF 算法由于没有对系统噪声统计特性进行在线估计, 其精度受载体机动影响较大, 图5 中天向位置误差表现比较明显。 对比图4 可知, 在100 s ~200 s、 250 s ~350 s 和400 s ~500 s 间, 当量测噪声服从非高斯分布时, 传统UKF 算法的滤波精度明显低于其他量测噪声服从高斯分布时的精度。 而本文提出的ADMCC-UKF 算法引入了对系统噪声统计特性的在线估计, 并根据迭代误差在线调整核宽大小, 能够取得更优的精度。 由图7 ~图9 可知, 在实际场景下的大部分时间中, ADMCC-UKF 算法可以取得比传统UKF 算法、 MCC-UKF 算法更低的位置误差。
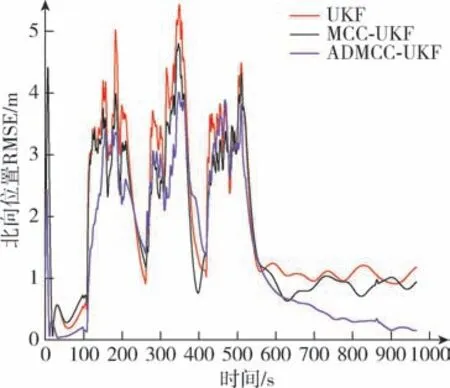
图5 北向位置仿真的RMSEFig.5 RMSE of simulation for north position
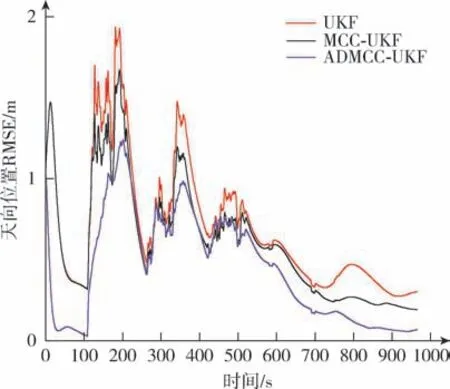
图6 天向位置仿真的RMSEFig.6 RMSE of simulation for upward positon
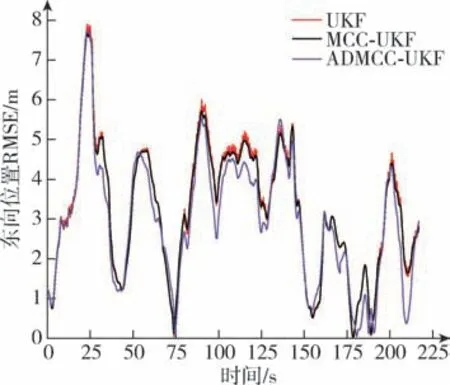
图7 东向位置实车的RMSEFig.7 RMSE of real vehicle for east position

图8 北向位置实车的RMSEFig.8 RMSE of real vehicle for north position
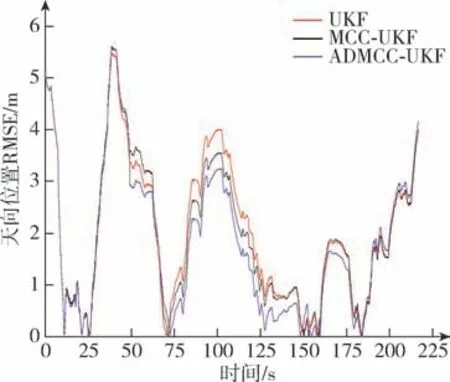
图9 天向位置实车的RMSEFig.9 RMSE of real vehicle for upward positon
图10 所示为100 s 时ADMCC-UKF 算法参数6次迭代的变化过程, 可以看出: 在迭代过程中,随着迭代误差绝对值增大, 核宽迅速增大, 削弱了较大误差的影响; 随着迭代误差绝对值减小,核宽迅速减小至阈值, 提高了解算精度。 由图10和表4 可知, ADMCC-UKF 算法充分利用了迭代过程中的误差信息, 可以较好地处理非高斯噪声的影响。 相比UKF 算法、 MCC-UKF 算法, ADMCCUKF 算法有更高的精度和鲁棒性。

图10 算法参数迭代变化Fig.10 Iterative change of algorithm parameters
从表3、 表4 数据可以看出, 传统UKF 算法精度最差, MCC-UKF 算法精度接近传统UKF 算法,本文提出的ADMCC-UKF 算法精度优于这两种算法。 在仿真实验中, ADMCC-UKF 算法相较于传统UKF 算法平均提高了19.27%, 相较于MCC-UKF算法平均提高了11.13%; 在实际实验中, ADMCC-UKF 算法相较于传统UKF 算法平均提高了12.55%, 相较于 MCC-UKF 算法平均提高了11.23%。
表5 数据取自PC 电脑仿真, PC 电脑的配置为: 处理器AMD Ryzen 9 3.3 GHz、 内存DDR4 3200MHz 32 G。 从表5 数据可以看出, 本文提出的ADMCC-UKF 算法运行时间略高于传统UKF 算法,但优于MCC-UKF 算法。
综上所述, 本文提出的ADMCC-UKF 算法可以有效处理系统噪声为非高斯噪声时带来的影响,能够取得优于MCC-UKF 算法和传统UKF 算法的精度, 同时计算量小于MCC-UKF 算法。 相比于传统UKF 算法提高的系统精度, ADMCC-UKF 算法提高的计算量可以接受。
4 结论
本文针对传统无迹卡尔曼滤波器在非高斯噪声情况下滤波精度下降的问题, 提出了改进的自适应变核宽相关熵ADMCC-UKF 算法。 首先根据惯性测量单元的基本情况构建系统噪声的粗略统计模型, 对量测噪声进行自适应估计; 然后引入核宽自适应算法, 在迭代过程中依据误差变化自适应调整核宽, 加快收敛速度; 最后通过基于最大相关熵准则的滤波器得到状态估计, 最终得到本文的ADMCC-UKF 算法。 相较于传统UKF 算法,该算法有较为明显的滤波精度提升; 相较于MCCUKF 算法, 该算法精度更高、 运行时间更短。 基于SINS/GNSS 组合导航系统对本文提出的算法进行仿真实验和实际跑车实验, 从滤波精度和解算时间两方面验证了本文所提算法的有效性, 对工程实践有一定的参考意义。

