I/F 电路线性度误差分析及补偿

同昭豫, 赵 鹏, 黄武扬, 王 豪, 张焜鋋

（西安航天精密机电研究所, 西安 710100）

0 引言

惯性器件在航空航天领域应用十分广泛, 作为惯导系统的核心器件, 石英挠性加速度计通过输出电流的大小来表示载体加速度的大小, 具有精度高、 抗干扰性好等一系列优点［1-3］。 石英挠性加速度计输出的电流模拟量需要通过模数转换电路转换为数字量, I/F 转换电路以其转换精度高、温度系数小、 对噪声具有平滑抑制作用等优点被广泛应用于惯导系统中［4-6］。

近年来, 惯性导航系统应用场景更为严苛,对加速度计的量程需求更高, 从以往的30g0提高到了60g0。 在保证分辨率的前提下, I/F 转换电路需要大幅提高工作频率［7-9］。 而在高工作频率下,分立器件特性会发生变化, 导致电流增大时电路的输出脉冲会产生非线性失真。 同时随着温度的变化, 元器件的参数特性会发生改变, 因此对I/F转换电路的线性度提出了更高的要求［10］。 针对I/F转换电路非线性失真问题, 目前常用的解决办法有三种: 第一种是增加硬件补偿电路, 通过硬件调试改善电路的线性度, 但是仅能补偿电路的一阶误差; 第二种是降低I/F 转换电路的工作频率,后级增加A/D 转换电路, 在不降低分辨率的前提下改善电路的线性度, 但是该方法需要增大电路体积, 且高精度A/D 转换芯片依赖进口器件［11］;第三种是对I/F 转换电路的输出脉冲进行脉冲补偿［12-13］, 但该方法仅从输出脉冲维度对线性度进行了补偿, 未考虑温度变化时硬件器件特性对线性度的影响。

本文提出了一种二级补偿算法, 该算法通过分析I/F 转换电路原理和元器件参数特性, 建立了电子开关漏电流和开关通断时间对线性度影响的误差模型, 分别对输出脉冲进行温度补偿以及全量程的线性度补偿, 在不进行硬件调试的情况下改善了电路的非线性失真, 一定程度上解决了量程与线性度互相矛盾的问题, 从而达到提高I/F 转换电路精度的目的。

1 线性度误差二级补偿模型

1.1 I/F 电路基本原理

I/F 转换电路基于电荷平衡原理完成对输入电流的量化, 主要包括积分器、 比较器、 FPGA 中的控制逻辑、 电子开关和恒流源。 I/F 转换电路的工作原理框图如图1 所示。

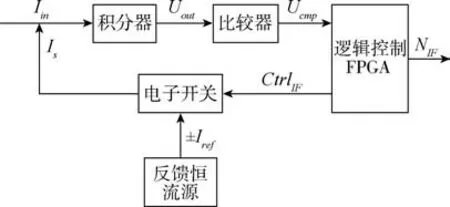
图1 I/F 转换电路的工作原理框图Fig.1 Working principle diagram of I/F conversion circuit

输入电流Iin在积分器上进行积分, 改变积分器输出电压Uout, 比较器电路处理Uout, 输出控制信号Ucmp, FPGA 解析比较器的输出信号Ucmp, 并以此为依据控制电子开关接通对应极性的反馈恒流源。 恒流源电路提供两路大小相等极性相反的恒值电流±Iref, 经过电子开关给积分器提供反馈电流Is。

反馈恒流源的接通时间以周期TIF为单位, 是TIF的整数倍。 一个时钟周期TIF内由反馈电流提供的电荷量记为一个量化电荷Qref, FPGA 在控制电子开关通断的同时, 对反馈恒流源进行计数, 得到某段时间内反馈恒流源Iref的接通周期数NIF。 量化电荷量Qs为

输入电荷量在一个时钟周期TIF内的电荷量为

根据电荷平衡原理, 一段时间内, 积分器上由输入电流Iin提供的输入电荷量和反馈电流Iref提供的量化电荷量应相同量化电荷

式（3）中,NIF也就是I/F 转换电路的输出脉冲,其理想情况下为

式（4）中,NIF为正比于Iin的线性函数, 但仅在理想状态下为常量。 实际上, 量化电荷Qref会随着输入电流的大小而改变, 也会随环境温度而改变, 导致I/F 转换电路的输出脉冲和输入电流呈非线性。

1.2 I/F 线性度误差模型建立

Iref为I/F 转换电路的反馈基准恒流源, 经过电子开关后直接进入积分器, 因此其主要误差来源于电子开关。 FPGA 在控制电子开关通断时, 电子开关会从两方面对线性度产生影响: 1）恒流源在接通和关断时, 其上升沿和下降沿（简称通断沿）存在接通时间和关断时间, 导致恒流源的接通时间不完全为时钟周期的整数倍, 如图2 所示; 2）电子开关中的开关管存在漏电流δIDSS, 当电子开关在工作时, 另一相电子开关的漏电流会流入, 影响反馈电流的大小, 如图3 所示。

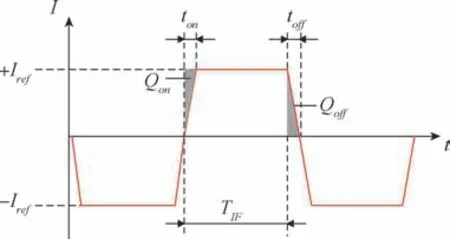
图2 接通时间、 关断时间示意图Fig.2 Schematic diagram of turn-on time and turn-off time

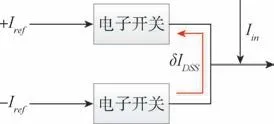
图3 电子开关漏电流示意图Fig.3 Schematic diagram of leakage current for electronic switch

首先分析开关通断沿对线性度的影响。 电子开关每控制恒流源进行一次开关所经过的时间即为一个关断时间和一个开通时间, 将开通时间内恒流源未提供给积分器的电荷称为δQon, 关断时间内恒流源提供给积分器的电荷称为δQoff, 因此某相恒流源导通一次, 对积分器电路提供的电荷实际大小为

故由通断沿影响, 某相恒流源导通一次实际提供的电荷量与理想状态下提供的电荷量之间的误差为

接下来考虑电子开关的漏电流带来的影响。在工作电路中, 某一相恒流源接通、 另外一相恒流源关断时, 由于开关管存在截止漏电流, 反馈电流会被另一相电子开关的漏电所影响。

设截止漏电流大小为δIDSS, 漏电流所引入的误差电荷量为

综合式（6） 和式（7） 可知, 电子开关工作一次,反馈电荷的误差为

将其代入式（4）中, 可得实际的输入电流和输出脉冲之间的关系为

由于硬件的器件特性, 每一次电子开关的开通时间和关断时间都有差异, 并且电子开关内部有输入电容Ciss、 输出电容Coss以及反向转移电容Crss, 随着输入电流的增大, 反馈脉冲个数增多,电子开关工作频率提高, 电容值也会发生变化,此时通断沿的时间会发生改变, 导致δQon和δQoff也发生改变。 因此,δQon和δQoff不是常量, 而是关于输入电流Iin的函数。 另一方面, 由元器件参数可知, 电子开关的漏电流会随温度变化而变化, 所以当输入电流为Iin、 环境温度为T时, 式（9） 可写为

由式（10）可知, 输出脉冲与输入电流之间本应呈线性关系, 但由于Iref存在非线性误差, 其实际的关系曲线如图4 所示。

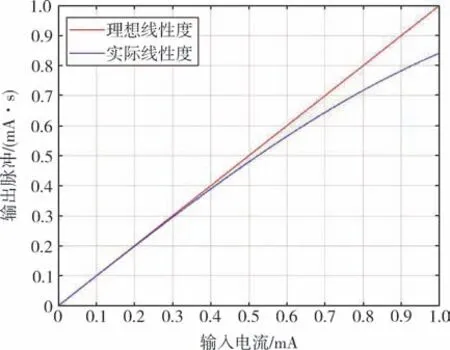
图4 脉冲输出的理想线性度与实际线性度示意图Fig.4 Schematic diagram of ideal linearity and actual linearity for pulse output

随着输入电流的增大, 电路的发热量增多,电子开关漏电流会发生变换; 与此同时, 电子开关工作频率也提高, 通断沿时间发生改变, 导致在工作电流逐渐增大时输出脉冲和输入电流呈现出了非线性关系。

1.3 I/F 线性度误差补偿模型建立

输出脉冲的误差来源于两个方面, 一个是温度变化引起的漏电流误差, 另一个是输入电流变化引起的电子开关通断沿的变化。 若仅在某个温度点下对不同输入电流的输出脉冲进行线性度补偿,则电路也仅在该温度点下呈现出良好的线性输出,变换应用场景后线性度则无法保证。 因此, 对线性度的误差补偿应从两方面进行, 一是通过温度补偿来保证温度对输出当量无影响, 二是补偿不同电流下的输出脉冲。 补偿流程图如图5 所示。

图5 二级补偿流程图Fig.5 Flowchart of secondary compensation

首先是温度补偿, 将单板放进温箱, 环境温度分别设置为-10℃、 15℃、 40℃、 65℃, 将电路板保温至环境温度后输入±1 mA 的电流, 测量至电路达到稳定工作状态, 分别得到正负向通道输出脉冲曲线, 选取指定温度下得到的一组有效数据作为基准建立温度误差模型, 温度拟合模型如下

式（11）中,α、β、γ为通过有效数据与当前温度T由最小二乘所拟合出的参数。

拟合后漏电流为常量, 此时式（10）可写为

由于输出数字量和输入电流之间的比例关系是一个与输入电流相关的函数, 对式（12）进行泰勒展开可得到

测量多组［Iin,NIF（Iin）］值, 则可用最小二乘法拟合出系数［NIF（0）,N′IF（0）,N″IF（0）］, 进而实现对线性度的误差拟合, 使得输入电流Iin和输出脉冲NIF呈线性关系。

2 实验验证

2.1 实验平台搭建

本文选用6166 恒流源来进行实验, 具体参数如表1 所示。 在实验过程中, 将I/F 转换电路固定在高精度温箱内。 通过对单路通道输入±1 mA 电流对I/F 转换电路的温度系数进行测试, 补偿后将I/F 转换电路放在常温环境中, 给该通道输入1 mA、2 mA、 3 mA、 5 mA、 8 mA、 10 mA、15 mA、20 mA、 30 mA、 40 mA、 50 mA、 60 mA 等典型电流值进行线性度测试。

表1 6166 恒流源参数Table 1 Parameters of 6166 constant current source

2.2 温度系数补偿

结合I/F 转换电路的特点, 在实验过程中, 将温箱温度分别设置在-10℃、 15℃、 40℃、 65℃,在各个温度点下保温1 h 以上, 使电路温度达到环境温度, 之后通电进行测试。

将各温度点下的输出脉冲连在一起并用式（11）进行数据拟合, 得到正向输出脉冲关于温度的拟合曲线, 如图6、 图7 所示。 负向输出脉冲与正向输出脉冲处理方式相似, 这里不再赘述。

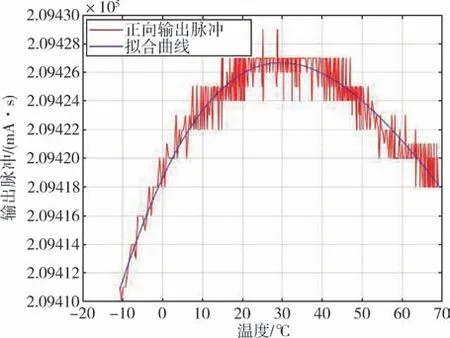
图6 正向输出脉冲温补前曲线Fig.6 Curve of positive output pulse before temperature compensation

图7 正向输出脉冲温补后曲线Fig.7 Curve of positive output pulse after temperature compensation

由图6、 图7 可知, 利用式（11）对正负通道各温度点下的输出脉冲建立的模型曲线能较好地描述数据特性, 以补偿漏电流对线性度的影响。 I/F模数转换电路温度系数通过计算-40℃～70℃输出脉冲方差与平均值的比值进行评估, I/F 转换电路温度系数所带来的误差从3.24 ×10-5降到7.67 ×10-6, 有效减小了温度环境变化给线性度带来的误差。

2.3 输出脉冲补偿

分别对I/F 转换电路单通道输入1 mA、 2 mA、3 mA、 5 mA、 8 mA、 10 mA、 15 mA、 20 mA、30 mA、40 mA、 50 mA、 60 mA 电流, 测试其输出脉冲。 将测试数据除以对应输入电流, 如: 输入电流为20 mA 时输出脉冲为4188440, 则处理后的数据为4188440/20 =209422; 输入电流为40 mA时输出脉冲为8372566, 处理后的数据为8372566/40 = 209314。 由此得到对应1 mA、 2 mA、 …、60 mA 等12 个测试点电流下的等效脉冲输出, 线性度指标通过计算12 个测试点等效脉冲输出的极差与平均值的比值进行评估。

在25℃的初始温度下测得原始脉冲数, 分别对其进行硬件补偿、 脉冲补偿和二级补偿。 脉冲补偿即不做温度补偿, 只做线性度输出脉冲补偿的算法, 再在40℃的初始温度下分别测量其线性度。

以处理后的输出脉冲为纵坐标、 输入电流为横坐标, 画出I/F 转换电路线性度补偿曲线, 如图8 所示。

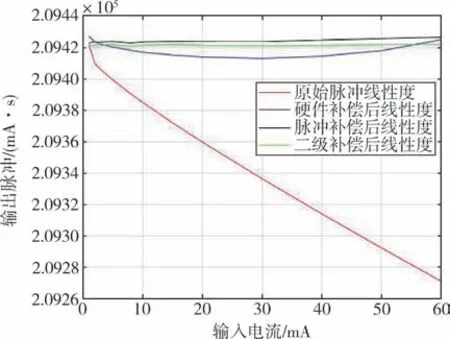
图8 I/F 电路线性度补偿前后的测试曲线Fig.8 Test curves of I/F circuit linearity before and after compensation

由图8 可知, I/F 电路补偿前线性度呈非线性递减, 存在高阶项。 硬件补偿可对电路中的一阶误差进行有效改善, 但是仍存在高阶非线性项。仅经过脉冲补偿的状态, 在改变初始环境后, 其线性度可达1.78 ×10-5, 而经过二级补偿后其线性度可达4.93 ×10-6, 一阶项、 高阶项以及温度系数均得到了补偿。 表2 中列出了通过逐级补偿得到的电路线性度指标, 可以看出二级补偿的效果明显优于硬件补偿和脉冲补偿的效果, 从而证明了二级补偿算法的有效性。

表2 I/F 电路线性度补偿前后的数据Table 2 Data of I/F circuit linearity before and after compensation

脉冲补偿未考虑环境变化的因素, 随着电路通电升温至稳定状态, 电子开关的漏电流会随温度变化而变化, 如果仅在某一温度点下进行脉冲补偿, 变换温度环境后会因为漏电流的改变使得线性度损失精度。 而二级补偿算法则充分考虑到这一点, 有效提升了I/F 转换电路的适应性和精度。

3 结论

本文针对I/F 转换电路非线性失真提出了一种二级补偿算法, 通过对电子开关漏电流和通断沿的误差参数进行误差建模, 得到温度补偿模型和脉冲补偿模型, 进行了全温全量程的线性度误差补偿。 实验结果表明, 经过二级补偿后的线性度指标得到了明显提升, 对环境温度有良好的适应性, 且不需要更改硬件电路, 有效提高了I/F 转换电路在大量程下的精度, 具有较高的工程应用价值。