基于模态辨识的多条件约束步态检测算法

孙银收, 熊 智, 邢 丽, 李晓东, 崔 岩

（1. 南京航空航天大学自动化学院, 南京 211106;2. 上海应用技术大学轨道交通学院, 上海 201418）

0 引言

近年来, 随着智慧城市建设和手持终端的普及, 基于位置服务（Location Based Service, LBS）的应用逐渐从特种专业领域走向大众消费用户, 高精度导航定位需求也逐渐从开放的室外区域延伸至复杂封闭的室内空间［1］, 而手持终端内嵌的惯性测量单元（Inertial Measurement Unit, IMU）为实现室内定位提供了基础。 曹骏等［2］利用智能手机通过行人航位推算（Pedestrian Dead Reckoning, PDR）方法和磁场匹配实现了室内定位; 徐雯琪等［3］设计了一种联合Wi-Fi 信息和PDR 算法的智能手机室内定位方法。 上述方法中, PDR 方法［4-5］凭借其自主性强、 复杂度低和成本小等优势引起国内外学者的广泛关注。

PDR 方法中稳健精准的步态检测是实现行人准确定位的首要条件。 KANG 等［6］通过快速傅里叶变换从传感器数据中提取频域特征, 从而实现计步; LU 等［7］、 刘杰等［8］采用峰谷检测方法, 提高了步态检测精度; XU 等［4］将峰谷值、 峰谷值时间间隔作为步态检测条件; PHAM 等［9］将峰值检测与最小峰距、 动态阈值等特征相结合, 减小了步态检测误差; 毕京学等［10］以智能手机为载体, 将有限状态与步行过程合加速度变化趋势相结合, 利用相邻合加速度差值和上/下坡次数阈值实现步数识别。 然而, 受行人不同运动状态和终端不同使用模式影响, 上述方法在连续运动模态下难以获得精确鲁棒的步态检测, 对此国内外学者开展了针对性研究。 GUO 等［11］通过提取传感器数据的时域特征, 利用主成分分析算法对其降维后, 采用随机森林以区分终端不同携带方式; 邓平等［12］通过分析和筛选加速度的时域特征, 构建线性支持向量机（Support Vector Machine, SVM） 多分类器,提出相邻步态约束法完成多种运动状态的准确识别, 并采用一种改进的单峰值检测法及零点搜寻规则, 实现了基于多种运动状态下均适用的步态检测方法; WANG 等［13-14］利用SVM、 有限状态机（Finite State Machine, FSM）和决策树（Decision Tree,DT）算法实现了行人运动状态和终端使用模式的识别, 根据识别结果提出了一种自适应波峰检测算法。 上述研究内容一定程度上提高了多运动模态的步态检测精度, 但依旧存在一些问题, 如: 识别的模态多关注行人运动状态与终端使用模式的组合, 对行人静止状态识别关注较少, 从而导致在非行走状态下的步态检测误识别; 在连续复杂模态下, 步态检测依旧存在过度计步或计步不足问题; 也有部分研究在遇到相邻波峰/波谷情况时往往选择前者较小伪波峰而忽略后者较大真波峰,难以满足连续运动模态下高精度轻量化步态检测需求。

围绕上述问题, 本文引入FSM 思想, 结合行人运动特性和终端日常使用习惯, 构建轻量化分类器识别行人三种运动状态（静止、 步行、 跑步）和终端三种使用模式（平端、 电话、 摆臂）, 以实现不同模态下步态检测阈值的动态调整。 而后, 根据模态辨识结果, 提出多条件约束步态检测算法,实现了单一和连续运动模态下的高精度步态检测。

1 信号特性分析及数据预处理

1.1 信号特性分析

在日常生活或特种作业中, 行人二维场景下所涉及的运动状态主要为站立静止、 步行和跑步;终端使用模式也多为平端、 电话和摆臂等。 结合行人使用习惯, 将两者组合为三种静止模态和四种运动模态（共计七种模态）, 并对其进行定义, 具体内容如表1 所示。

表1 模态分类及定义Table 1 Classification and definition for modal

不同模态下的IMU 数据特征不同, 图1 为平端静止、 平端步行、 摆臂步行三种模态下的数据特征示意图。 由图1 可知, 平端静止模态下, 数据波动较小, 加速度计X轴、Y轴、 陀螺仪三轴数据近似为零,Z轴加速度、 模值两者大小近似重力;平端步行模态下, 由于足部的升降起伏和躯干的左右旋转, 加速度、 角速度数据呈现规律性波动,一般为先波峰后波谷, 加速度模值数据近似正弦曲线, 并且两个连续波峰或波谷代表一个单步,即行人左右足跟或足尖先后着地, 电话步行模态与之类似; 摆臂步行模态下, IMU 数据既反映行人足部运动特征, 也受手部周期性摆动影响, 加速度模值呈现规律性波动, 出现大小波峰现象,而Z轴角速度数据近似正弦曲线, 并且一个波峰或波谷代表一个单步, 两个连续波峰或波谷代表一个复步, 即同侧足跟或足尖前后两次连续着地。

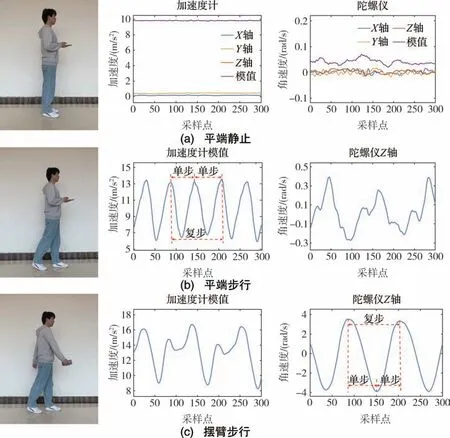
图1 模态展示及其数据特征Fig.1 Schematic diagram of modal presentation and its data characteristics

1.2 数据预处理

手持终端内置的IMU 基本为低精度消费级,而且由于手部微小抖动和电子器件之间的噪声影响导致加速度、 角速度数据包含大量噪声, 对模态辨识和步态检测造成干扰。 因此, 需要对IMU数据进行预处理。

本文选取Savitzky-Golay（S-G）滤波器［15］进行数据预处理。 该方法是一种时域平滑方法, 可以对窗口内的数据进行加权滤波, 采用最小二乘卷积对局部数据进行高阶多项式拟合, 在去除高频噪声的同时可以有效保留信号的变化信息。 该方法有两个重要参数, 即窗口大小和拟合阶数, 窗口越大越容易丢失有效信号而且滤波滞后现象越严重, 阶数越大去噪能力越差。 在本文中, 综合考虑数据处理的时效性和滤波效果, 将S-G 滤波窗口设置为51, 阶数设置为1, 图2 为电话步行模态下加速度模值滤波前后对比图。 由图2 可知, S-G 滤波很好地滤除了原始数据中的高频噪声, 并且基本保留了数据特征。

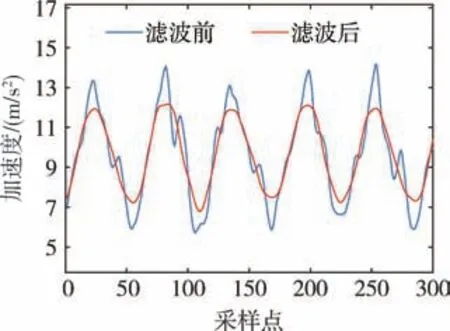
图2 电话步行模态下滤波前后的加速度模值对比Fig.2 Comparison of acceleration modulus under telephone walking modal before and after filtering

2 基于FSM 的模态辨识方法

一般情况下, 行人的运动状态和终端使用模式会对IMU 数据产生较大影响, 使得不同模态下的数据特征不同。 如图3 所示, 不同的数据特征尽管会干扰步态检测, 但其多样化的时域特征也便于模态辨识。 因此, 可以借助IMU 数据不同的时域特征识别不同运动模态来动态调整步态检测算法中的相关参数, 以增强PDR 算法的适应性和定位导航性能。 在FSM 模型中, 当一个条件被满足,执行一次状态转换, 未检测到状态切换则保持当前模态［16］。 因此, 将FSM 模型用于模态辨识可以即时地响应不同模态切换, 从而识别各种模态并且减轻终端计算负荷。

图3 连续不同模态下的数据特征Fig.3 Data characteristics under continuous different modals

2.1 行人运动状态识别

图4 为行人运动状态识别的FSM 模型。 在模型中, 行人运动状态共分为三种: 站立静止、 步行、 跑步。 当行人静止时, 角速度模值Ng保持相对稳定, 变化幅度极小; 当行人运动时, 陀螺仪受多方面因素影响, 其模值会产生较大波动。 因此, 通过角速度模值Ng可以识别行人静止和运动两种状态, 其计算方式如式（1）所示。 此外, 行人在跑步时的运动强度远大于步行状态, 借助加速度计X轴方差数据可以区分行人跑步和步行状态, 其计算方式如式（2）所示。

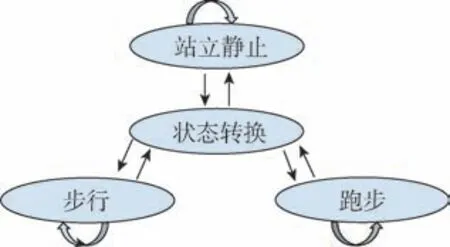
图4 行人运动状态识别的FSM 模型Fig.4 FSM model for pedestrian motion state identification

式（1） 中,gx、gy、gz分别为陀螺仪X轴、Y轴、Z轴的数据。

2.2 终端使用模式识别

图5 为手持终端使用模式识别的FSM 模型。在模型中, 终端使用模式有平端、 电话和摆臂三种。 由图3 分析可知, 不同模式下加速度数据不同, 因此利用加速度计X轴、Z轴滑动窗口内的均值, 即可以进行分类, 计算方式如式（3）、式（4）所示。

图5 手持终端使用模式识别的FSM 模型Fig.5 FSM model for handheld terminal using pattern identification

将行人运动状态识别结果与终端使用模式辨识结果进行组合, 由此实现七种不同模态的归纳和辨识, 整体识别过程如图6 所示。 需要说明, 本文只研究了站立静止、 步行和跑步三种静止模态,并不涉及其他静止模态。

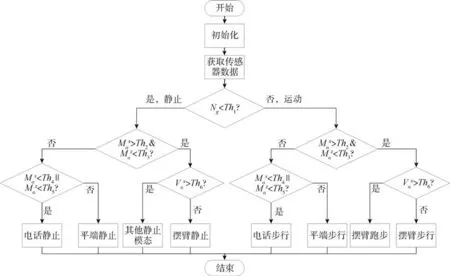
图6 模态辨识流程图Fig.6 Flowchart for modal identification

3 多条件约束步态检测算法

由图1、 图3 分析可知, 不同模态下IMU 数据特征不同。 静止模态下行人没有行进, 数据波动较小, 此时不进行步态检测, 可以消除非行走状态下的步态检测误差; 运动模态下IMU 数据均呈现规律性波动, 变化趋势一般为先波峰后波谷。然而, 不同的运动模态使得IMU 各轴方向、 数据不同, 影响了步态检测精度。 为了进一步降低不同运动模态对步态检测的影响, 针对平端步行、电话步行两种模态采用加速度模值进行步态检测;摆臂步行、 摆臂跑步两种模态的加速度数据成分复杂, 既反映了行人身体重心的升降, 也包含有手部周期性摆动特征, 其形成的大小波峰现象不利于步态检测, 较易引起步态漏检或误检, 而陀螺仪Z轴数据主要反映手臂周期性摆动特性。 此外, 从人体运动学角度出发, 手部周期性摆动与足部的步态周期相对应, 利于步态检测。 因此,在这两种模态下采用陀螺仪Z轴数据进行步态检测。 不同运动模态下传感器数据的选取如表2 所示, 并且将检测到一个单步作为计步规则, 多条件约束步态检测算法具体步骤如下所示。

表2 运动模态下的计步数据与规则Table 2 Pedometer data and rules in motion modal

3.1 极值约束

行人运动会引起IMU 数据出现波峰/波谷, 但由于手部的抖动和电子器件间的噪声影响, 在对数据滤波后依旧存在较多杂峰/杂谷, 因此需要通过极值约束来排除杂波影响。 以极大值imax为例,其判断条件为当前值ij大于阈值Tp, 且在一定范围内为最大值, 具体如式（5）所示, 极小值imin与之类似。

式（5）中,Ca、Cb为计数值且初值为0, 其计算规则如下

式（6）、 式（7）中,k=1, 2, 3, …, 10。

3.2 周期性约束

当检测到极值时, 需要考虑两个连续波峰或连续波谷之间的时间间隔T1以消除部分无效极值。此外, 处于摆臂步行、 摆臂跑步模态时, 一个波峰或波谷代表一个单步, 因此需要设置相邻波峰与波谷之间的时间间隔T2并应用至全局。 行人的步态周期一般为1 Hz ～3 Hz［16］, 但行人跑步状态的快速性会导致摆臂跑步模态下的时间间隔有所减小, 故时间间隔T1、T2可根据实际情况做相应调整。 若当前极值满足周期性约束, 可以确定其为峰值Tj或谷值Vj, 并令峰值标签或谷值标签为1, 判断条件如式（8） 所示。 需要注意的是,IMU 数据波形是先波峰后波谷, 当检测到谷值时,应当取当前谷值与当前峰值间的时间间隔进行判断, 如式（9）所示。

式（8）中,j表示第j步。

3.3 峰谷值匹配机制

不同模态下IMU 数据波形特征基本一致, 往往先出现波峰后出现波谷且两者在时序上交替出现。 周期性约束结束后, 不同模态下均将单步作为步态检测标准, 检测到单步时令步态标签Sj为10。 因此, 当行人处于平端步行（m=1）、 电话步行（m=2）模态时, 将出现一次峰值和谷值视为一步;当行人处于摆臂步行（m=3）、 摆臂跑步（m=4）模态时, 以出现一次峰值或谷值作为一步, 具体如下

3.4 相邻波峰/波谷替代机制

在实践过程中发现, 完成峰谷值匹配后依旧存在满足极值约束、 时间阈值T2而不满足时间阈值T1的情况, 即出现了相邻波峰或波谷, 从而导致波峰/波谷误识别, 具体如图7 所示。 误识别现象往往会干扰步态检测, 降低步长估计的准确度,最终影响导航定位精度。 因此, 通过相邻波峰/波谷替代机制以纠正误识别现象, 即通过对当前峰值imax或谷值imin进行判断, 如果大于上一峰值Tj或小于上一谷值Vj, 说明上一个步态检测中的峰值/谷值为伪波峰/波谷, 剔除伪波峰/波谷, 保留真波峰/波谷, 并更改步态检测结果。

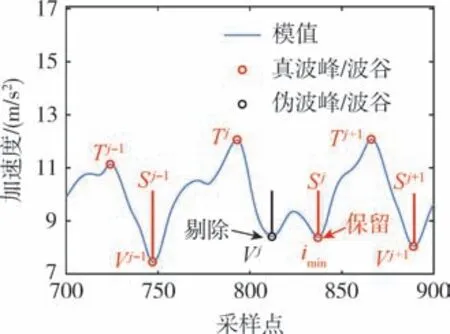
图7 相邻波峰/波谷误识别情况示意图Fig.7 Schematic diagram of adjacent peak/valley misidentification

4 实验验证与结果分析

为了充分验证本文步态检测算法的有效性,设计了两类实验进行验证, 并与峰值检测算法、峰谷检测算法进行对比。 实验设备为Redmi Note 11T Pro, 将2022 年IPIN 比赛发布的GetSensorData［17］作为数据采集软件, 采样频率为100 Hz, 实验场景为南京航空航天大学自动化学院1 号楼5 楼,如图8 所示。 此外, 为了评估步态检测效果, 采用式（11）、 式（12）计算计步误差E、 步态检测精度A。

图8 实验装备和实验场景Fig.8 Diagram of experiment equipments and experiment scenarios

式（11）中,St和Sc分别为真实步数和算法估计步数。

4.1 步态检测参数

由于不同模态下IMU 数据特征明显, 与模态辨识相关的参数选取较为简单, 而步态检测参数即检测阈值、 时间间隔难以确定。 因此, 只针对步态检测参数做具体讨论, 为了获取合理参数,每种运动模态各行进90 步进行相关参数统计。

（1）检测阈值

图9 为不同模态下每一步的峰值、 谷值统计量。 由图9 分析可知, 平端步行与电话步行两种模态下的数据接近, 峰值一般大于10.96 m/s2, 谷值一般小于9.05 m/s2; 摆臂步行模态下, 峰值中最小量为1.78 rad/s, 谷值中最大量为-1.80 rad/s;摆臂跑步模态下, 峰值中最小量为4.54 rad/s, 谷值中最大量为-2.78 rad/s。 摆臂步行模态和摆臂跑步模态的数据相差较大, 但存在包含关系。 为了避免波峰/波谷漏选, 数值选取需要有一定冗余, 并且需要尽可能减少参数数量以增加鲁棒性,数据选取如表3 所示。

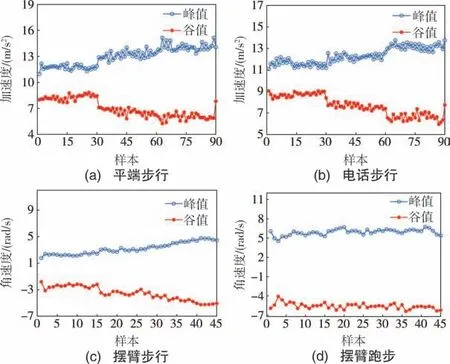
图9 检测阈值统计量Fig.9 Diagram of detection threshold statistics

（2）时间间隔

图10 为不同模态下每一步的峰谷值间、 峰峰值/谷谷值间的时间间隔。 由图10 可知, 在平端步行与电话步行两种模态下, 峰谷值间、 峰峰值/谷谷值间的时间间隔均大于0.21 s、 0.49 s; 在另外两种模态下, 峰谷值间的时间间隔均大于0.24 s,峰峰值/谷谷值间的时间间隔均大于0.74 s。 与检测阈值选取原则类似, 时间间隔选取数据如表4所示。

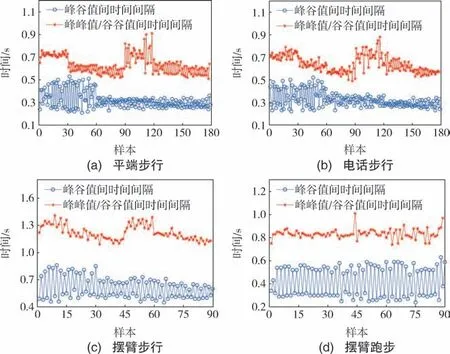
图10 时间间隔统计量Fig.10 Diagram of time interval statistics

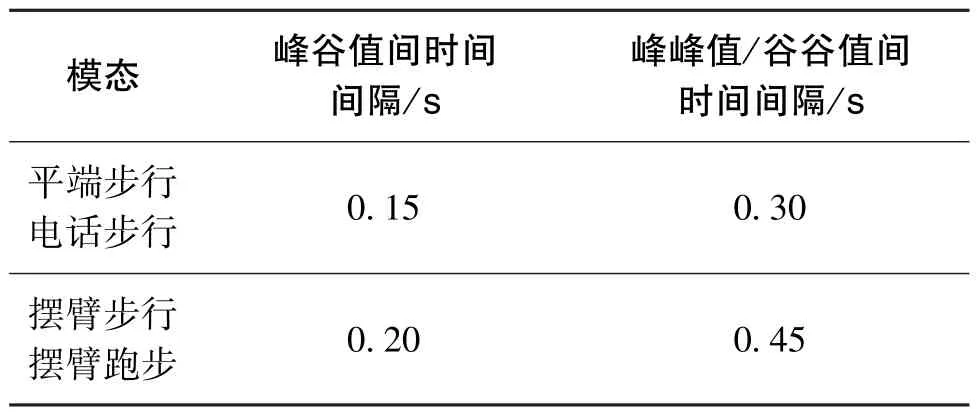
表4 时间间隔的选取Table 4 Selection of time interval

4.2 单一运动模态下的步态检测实验

测试人员在单一运动模态下以不同速度, 即在慢速、 正常、 快速三种模式下进行实验, 每种模式下采集三组数据。 实验时, 测试人员首先保持相应的静止模态, 固定行进90 步, 不限制人员拐弯。 其中, 摆臂跑步由摆臂静止模态出发, 最后测试人员以相应的静止模态停止运动。 此外,也在相同模态下以不同速度连续行进90 步并采集一组数据。 实验结果如表5 所示, 本文算法与其他算法的实验结果对比如图11 所示。

图11 与其他算法的实验结果对比Fig.11 Comparison of experiment results with other algorithms

表5 单一运动模态下的步态检测结果Table 5 Gait detection results under a single-motion modal

由图11 可知, 峰值检测和峰谷检测算法在平端步行、 电话步行模态下的步态检测效果较好,计步误差最大分别为7.78%、 10.00%, 而且峰值检测算法在两种模态下的平均计步误差分别为3.33%、 3.21%, 高于峰谷检测算法的1.73%、1.23%; 在摆臂步行与摆臂跑步模态下, 两种算法的计步性能有所下降, 最大计步误差分别为18.89%、 33.33%, 峰值检测算法的平均计步误差分别为3.09%、 11.85%, 而峰谷检测算法的平均计步误差分别为8.89%、 6.42%。 原因在于前两种模态主要反映行人行走特征, 而后两种模态在含有行人行走特征之外, 也受手臂周期性摆动影响, 其形成的大小波峰现象不利于步态检测。 本文所提算法在不同模态不同速度下均保持较高的计步精度, 最大计步误差为1.11%, 平均计步误差为0.11%, 较另外两种算法有显著提高, 最大提升分别为18.89%、 33.33%, 平均提升4.43%、5.24%。

4.3 连续复杂模态下的步态检测实验

为进一步验证本文算法在连续复杂模态下的稳定性与可靠性, 测试人员在相同实验场景中以不同模态（本文定义的七类模态）连续行进, 每个模态固定行进90 步, 并在第50 步结束时保持静止一段时间而后继续行进（摆臂跑步过程中不要求静止）。 整个实验过程对速度不做限制且行进过程中进行多次模态切换, 最终累计行进360 步（三种静止模态行进步数为0）, 全程约310.50 m。 同时,本文为了保证步态检测方法的对比有效性, 在运行峰值检测、 峰谷检测算法时均采用了本文的模态辨识方法, 且步态检测阈值与本文方法保持一致, 步长模型也均采用文献［18］中所记录的方法。本文的步态检测实验结果如图12 所示。 为了在图形中更好地展示数据, 对模态辨识与步态检测结果进行相应调整, 但两者意义一致。

图12 连续复杂模态下的步态检测结果Fig.12 Gait detection results under continuous complex modals

表6 为本文算法与其他算法的实验结果对比。可以发现, 在连续复杂模态下, 峰值检测和峰谷检测算法分别误检或漏检了11 步、 12 步, 总体计步误差分别为3.06%、 3.33%。 数据表明, 在连续复杂模态下, 由于存在较多模态以及伪波峰/波谷, 导致峰值检测和峰谷检测算法适应性差, 存在计步不足或过度计步的问题。 在连续复杂模态下, 本文算法总体检测精度为100%, 整体计步性能较峰值检测和峰谷检测算法分别提升了3.06%、3.33%, 准确性和鲁棒性方面有了明显提高。 统计单独每个模态下的数据, 三种算法在静止模态下的检测精度均为100%, 部分证明了本文所提基于FSM 的模态辨识方法的有效性, 即仅在运动时进行步态检测。 在运动模态下, 峰值检测算法在电话步行时检测效果较好, 在平端步行、 摆臂跑步时检测效果次之, 在摆臂步行时检测效果最差, 计步误 差 分 别 为 1.11%、 5.56%、 5.56%、11.11%; 峰谷检测算法在平端步行时步态检测效果最好, 电话步行次之, 之后依次为摆臂跑步、摆臂步行, 计步误差分别为 0%、 2.22%、5.56%、 10.00%。 而本文所提算法在单独每个模态下步态检测精度均达100%, 相较于另外两种算法, 计步性能最大分别提升了11.11%、 10.00%,也证明了本文步态检测算法中数据选取的合理性和优势, 即平端步行、 电话步行模态下通过加速度数据进行步态检测, 摆臂步行、 摆臂跑步模态下采用陀螺仪数据进行步态检测。

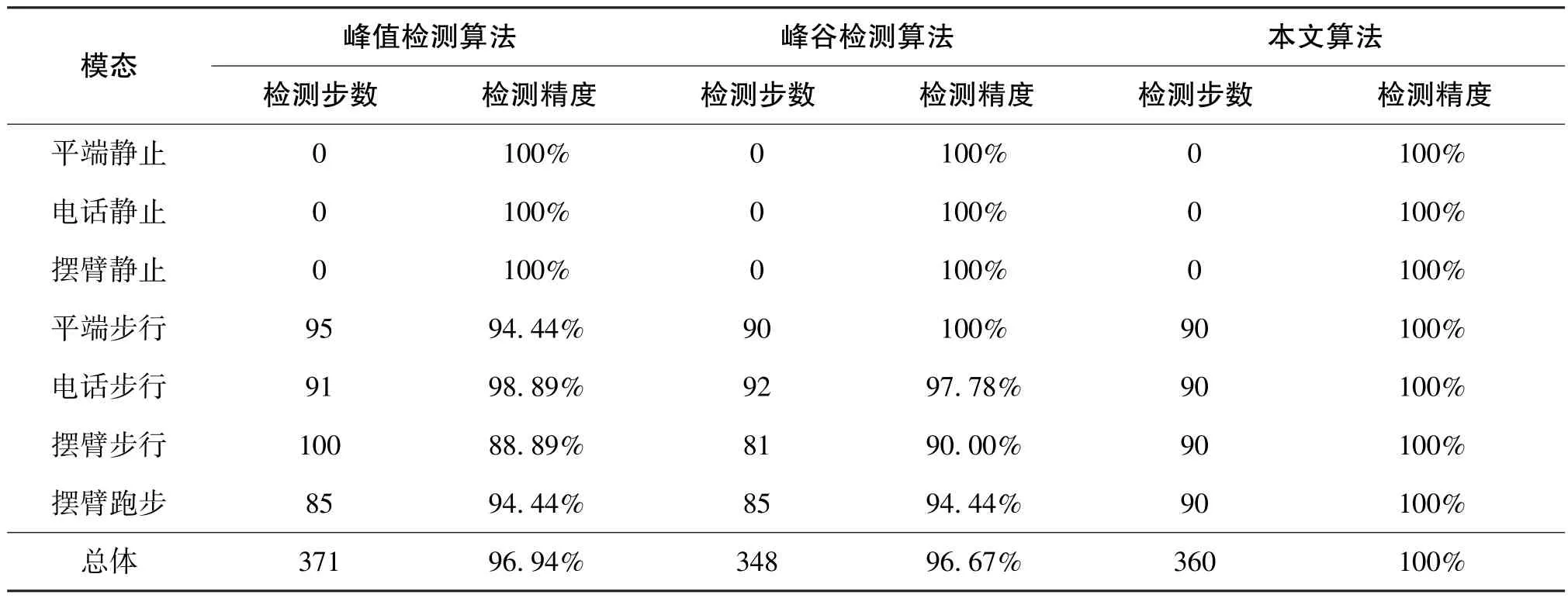
表6 连续复杂模态下的实验结果对比Table 6 Comparison of experiment results under continuous complex modals

图13（a）为本文算法在连续复杂模态下的运动轨迹及模态辨识结果, 结合图12 可以分析得到,本文所提基于FSM 的模态辨识方法应用效果较好,没有运动状态相互紊乱的现象, 在连续复杂模态下依旧可以识别平端静止、 平端步行、 摆臂跑步等七种模态, 使得步态检测算法可以自适应调整检测阈值, 一定程度上提高了算法的适应性。图13（b）为峰值检测算法、 峰谷检测算法以及本文算法在连续复杂模态下的运动轨迹, 分别用蓝色、橙色以及红色曲线表示, 图中的黑色曲线为参考轨迹, 绿色点为误差评估点, 由轮式里程计标定,整个实验过程行走约310.50 m。 实验结果为: 峰值检测算法的终点误差为7.03 m, 平均误差为6.31 m; 峰谷检测算法的终点误差为14.36 m, 平均误差为8.40 m; 而本文算法的终点误差为5.30 m,平均误差为4.35 m, 均优于另外两种对比算法。 数据表明, 本文算法通过施加多种约束条件可以识别真正的波峰/波谷, 解决了过度计步和计步不足的问题, 提高了连续复杂模态下计步性能的同时也提升了定位精度, 这也是本文算法优于另外两种算法的原因所在。

图13 连续复杂模态下不同算法的运动轨迹Fig.13 Motion trajectories of different algorithms under continuous complex modals

5 结论与展望

本文针对传统步态检测存在检测精度较低的问题, 在其理论基础上提出了基于模态辨识的多条件约束步态检测算法。 通过实验确定不同模态下的检测阈值, 引入FSM 模型识别行人三种运动状态和终端三种使用模式并进行组合, 累计七种模态, 针对每种模态可以自适应选择阈值; 在此基础上, 利用极值约束、 周期性约束、 峰谷值匹配机制、 相邻波峰/波谷替代机制等四种约束条件识别步态。 该算法相较于峰值检测、 峰谷检测算法, 在单一运动模态下步态检测精度平均提升了4.43%、 5.24%, 在连续复杂模态下整体计步性能分别提升了3.06%、 3.33%, 解决了过度计步和计步不足的问题, 提高了步态检测精度, 为后期提升PDR 定位性能奠定基础。