基于强化学习的多机器人系统的环围编队控制

韩艺琳　王丽丽　杨洪勇　范之琳

摘要： 针对机器人对未知目标的编队跟踪问题，建立机器人运动控制模型，提出了基于强化学习的目标跟踪与环围控制策略。在强化学习策略驱动下，机器人探索发现目标点位置并展开跟踪，使用环围编队运动模型对机器人跟踪策略进行实时优化，实现对逃逸目标点的动态跟踪与环围控制。搭建了多机器人运动测试环境，实验表明结合强化学习的方法能够缩短多机器人编队调节时间，验证了多机器人环围编队控制策略的有效性。

关键词： 运动控制；强化学习；目标跟踪；环围控制

中图分类号： TP273+.5文献标识码： A

Ring-around Formation Control of Multi-robot Systems Based on Reinforcement Learning

HAN Yilin， WANG Lili， YANG Hongyong， FAN Zhilin

Abstract：For the robot formation tracking problem of unknown target， a robot motion control model is established， and a target tracking and ring-around control strategy based on Reinforcement Learning（RL） is proposed to solve the problem. Driven by RL， the robot explore the location of the target point and initiate tracking. The robot tracking strategy is optimized in real time using the ring-around formation motion model to achieve dynamic tracking and ring-around control of the fleeing target point. A multi-robot motion control environment is established， and the experiments indicate that the combined RL can accelerate the multi-robot formation adjustment time and prove the efficiency of the multi-robot ring-around formation control strategy.

Key words： motion control; reinforcement learning; target tracking; ring-around formation control

0 引言

近年來，多机器人系统以其执行效率高、功能多样、任务分配合理[1]等特点受到越来越多学者的重视，通过在系统内部建立多机器人之间合理的约束控制与协同策略，使多机器人系统能够处理大部分单机器人难以应对的复杂问题。比如在协同探索[2]和轨迹跟踪[3]等领域中，采用多机器人编队协作、运动学控制等方法能够实现对系统的一致性控制。因此，编队和运动学[4]约束组成的协同控制方法，成为解决复杂情况下多机器人系统问题的重要研究方向。

针对多机器人编队系统，常用方法有模糊PID法[5]、神经网络[6]、强化学习[7]等。其中，神经网络将关注点放在处理机器人与目标点的跟踪训练与路径规划方面，对控制算法要求较高，且训练时间长，不适用于动态未知环境；模糊PID法对环境依赖较小，但缺乏对系统整体的规则设定，难以得到整体的决策。为提高机器人对环境的适应度，Yu等[8]结合模糊控制与神经网络，提出一种容错控制策略，实现在复杂环境下的同步跟踪控制，Zhang等[9]提出一种基于自适应差分的多无人机编队预测控制算法，实现对运动轨迹的自适应调整。为避免机器人的路径轨迹与任务目标不匹配[10]情况，Loris等[11]提出结合迭代学习和强化学习的方法，实现学习算法控制器参数的在线调整与轨迹跟踪控制。相比其他方法，强化学习善于在线处理环境信息，能够搭载其他路径规划算法，更有利于实现多机器人编队寻找最优路径。

目标环围控制是多机器人系统对目标点进行编队包围的一种特殊状态，主要利用了多机器人系统的路径规划、协同编队和跟踪控制等相关控制技术，完成机器人规划最优路线、切换环形编队、对逃逸目标点以环围编队形式进行追踪等任务。对于目标信息不确定的环境，Gao等[12]提出了一种基于向量场的分布式控制策略，使用分布式控制率进行目标状态估计，实现了多机器人系统的期望运动；Chou等[13]将目标搜索算法与PID控制结合，实现机器人在未知环境中的自主避障与导航。对于带有逃逸功能的目标点，可以利用机器人速度和运动学的差异弥补间距[14]上的不足，Yao等[15]提出了一种用于主动目标跟踪的随机非线性模型预测控制（SNMPC）算法，实现多机器人对目标的环航控制；Lu等[16]提出了基于激光测距仪的目标检测和跟踪算法，实现移动机器人对运动目标的实时跟踪。

现有研究多数仅讨论了多机器人对逃逸目标点的合作控制[17]，缺少对多机器人协同编队和避碰的考虑。基于此，本文拟研究基于强化学习的多机器人系统的环围编队控制，利用分布式思想为机器人协作提供通信支持，机器人在强化学习算法训练下探索接近目标点的最优轨迹，结合运动学模型用于控制多机器人环形编队。除此之外，在环形编队控制器基础上，基于强化学习的多机器人系统要实现对目标点的环围控制，为多机器人系统设计合理的目标追踪策略，以及处理追踪和编队过程中各个机器人之间路径冲突和避碰的策略。

1 研究目标

本文主要利用强化学习方法解决多机器人系统的环围编队控制问题，针对此类问题可分解为两个步骤：目标跟踪和目标环围。一是建立环境势场，机器人对目标进行识别跟踪，逐步进入环形编队状态；二是目标点逃逸时，多机器人的运动控制与强化学习训练相结合进行协作围捕，直至达成合理的集体决策[18]。

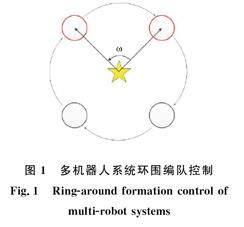
假设多机器人系统中的各机器人与坐标中心的连线为轴线，为保持相邻轴线之间的角度稳定，通过调整每个机器人的位置，保证轴线之间恒等的角度。多机器人系统环形编队控制如图1所示。

其中，五星区域表示多机器人系统坐标中心点，ω为编队稳定时邻居机器人轴线之间的期望夹角，当多机器人之间保持大小为ω的夹角并均匀分布在环形轨迹上，表示多机器人系统实现环围编队控制，在有N个机器人的编队系统中，ω数值计算为

（1）

2 基于强化学习的多机器人编队目标环围算法设计

2.1 多机器人系统的强化学习

强化学习以马尔科夫过程为理论研究基础，马尔科夫决策过程可以被看做一个五元组〈S，A，R，P，γ〉，其中，S为系统状态空间，A为系统动作空间，P为状态转换概率，R为状态回报，γ为学习过程折扣因子，该过程指的是在与环境进行交互后，得到不同的回报并评估当前采取的动作，形成自身的经验策略π。

一般情况下，强化学习中的回报以累积经验的方式表示：

（2）

其中，r为瞬时回报，t为运动时刻，j为执行步数。

对于多机器人系统的强化学习过程，当系统处于状态st={s0，s1…，sN}，联合策略可以表示为π（st|ut）。为使多机器人系统采取的联合策略接近于最优策略π（st|u′），使用强化学习方法中的经典算法Q-Learning算法进行策略优化。计算每个机器人在动作策略ut下的状态-动作值函数为

3 实验验证

为验证基于强化学习的多机器人系统的环围编队控制算法的有效性，设定多组不同的起始点和目标机动环境，对具有逃逸能力的目标点进行自由追踪，设定初始逃逸速度vg=0.3，随着环围编队的稳定，目标点由于受到阻力而被逼停，最终vg=0。多机器人起始速度分别设置为：v1=0.6，v2=0.5，v3=0.4，v4=0.3。

假设多机器人系统在静态和动态环境下移动，多机器人系统运动后留下的曲线轨迹分别如图2和图3所示，多机器人速度和转动量变化分别如图4和图5所示，多机器人系统的收敛速率如图6所示。

静态环围控制轨迹如图2所示，机器人在与环境的交互过程中，考虑周围邻居的状态和速度信息，实时调整自身的动作避免发生碰撞，使接近目标点的路线为最优路径，实验结果证明了改进强化学习算法可以实现多机器人对静态目标的围捕。

在动态环境中，多机器人在接近目标点的最小安全范围内进行动态环围，由于环航编队前期，机器人需要考虑包括邻居机器人和目标点在内的斥力，以及目标追踪阶段中指向目标点进行环航编队的引力，因而该过程中存在轨迹波动，形成编队队列的难度较大，如图3所示。当目标点发生不确定方向位移时，多个机器人使用强化学习方法在线调整速度控制器，使编队系统能够在运动学模型控制下进行跟踪控制，并根据转向角度和速度调整编队距离，由于环航编队的特性，此时速度收敛较慢。當多机器人系统形成较为稳定的编队后，机器人所受到的势场力逐渐减小到0，得到稳定的编队环围策略。

图4所示为多机器人系统环围动态目标点的速度变化过程，为机器人设计带有加速度的控制器，当机器人接近目标点的安全距离时，进入环航编队并与邻居机器人获得通信，对逃逸目标点展开追踪。图5表示多机器人系统环围动态目标点的转动量变化过程，随着多机器人完成跟踪目标点进入环围阶段，多个机器人的转动量逐渐收敛并达到一致。当机器人在强化学习与动力学模型的交互作用下，找到满足编队约束的动作策略后，与邻居机器人进行通信并调整自身速度与转动量，因此当多机器人在环围轨迹上学习到最优速度和角度转动量时，多机器人系统达到最优，多机器人可保持在最优轨迹上环围。

图6展示了多机器人系统中每个机器人随Q值训练步数的变化，在目标跟踪阶段采取人工势场法作为目标导向，机器人探索路径过程中耗费代价小，机器人策略生成速度加快。随多机器人系统迭代训练步数的增加，机器人累积奖赏增多，当训练经过350步后，多机器人系统基本达到环围状态，此时系统内部相对稳定。当多机器人系统学习到稳定的策略时，受势场影响小，机器人Q值达到最大，多机器人系统实现对目标点的环围编队控制。综上所述，本文使用控制器对强化学习过程进行改进，机器人能够快速学习到跟踪与环围策略，并维持系统稳定。

4 结论

本文基于强化学习设计了多机器人环围编队控制系统，采用分布式设计思想降低系统内的通信损耗，编队中的机器人只能接收到邻居机器人的信息。同时，将强化学习算法中训练与寻优的性能与机器人运动学模型相结合，编队和环围轨迹不再依赖训练后得到的策略，利用结合强化学习的速度控制器规划最优轨迹，从而在较短时间内达到期望的环围效果，不需通过反复多次的实验训练，仍能收敛到速度一致状态。

虽然机器人环围编队控制系统能够实现路径收敛，但是当目标点数量增加时，需要将多个机器人进行合理分组跟踪，分组机器人之间可能存在协作与竞争的关系，都会影响算法的收敛速度。因此，接下来将针对不确定环境下的多机器人分组一致性进行研究。

参考文献：

[1]YAN Z， JOUANDEAU N， CHERIF A A. A survey and analysis of multi-robot coordination[J]. International Journal of Advanced Robotic Systems， 2013， 10（12）：399.

[2]QU Y， SUN Y， WANG K， et al. Multi-UAV Cooperative Search method for a Moving Target on the Ground or Sea[C]//2019 Chinese Control Conference （CCC）. GuangZhou，  China： IEEE， 2019： 4049-4054.

[3]KAMALAPURKAR R， ANDREWS L， WALTERS P， et al. Model-based reinforcement learning for infinite-horizon approximate optimal tracking[J]. IEEE transactions on neural networks and learning systems， 2016， 28（3）： 753-758.

[4]路兰，殷水英. 基于空间交互作用的中国省际人口流动模型研究[DB/OL]. （2023-08-08）[2023-08-15].https：//link.cnki.net/urlid/11.1115.F.20230808.1339.004.

LU L， YIN S Y. Study on the model of inter-provincial population flow in China based on spatial interaction[DB/OL]. https：//link.cnki.net/urlid/11.1115.F.20230808.1339.004.

[5]MOHAN B M， SINHA A. The simplest fuzzy PID controllers： mathematical models and stability analysis[J]. Soft Computing， 2006， 10（10）： 961-975.

[6]于欣波，贺威，薛程谦，等.基于扰动观测器的机器人自适应神经网络跟踪控制研究[J].自动化学报， 2019， 45（7）：1307-1324.

YU X B， HE W， XUE C J， et al. Research on robot adaptive neural network tracking control based on disturbance observer [J]. Journal of Automation， 2019，45（7）：1307-1324.

[7]徐鵬，谢广明，文家燕，等.事件驱动的强化学习多智能体编队控制[J].智能系统学报， 2019，14（1）：93-98.

XU P， XIE G M， WEN J Y， et al. Event driven reinforcement learning multi-agent formation control [J]. Journal of Intelligent Systems， 2019，14（1）：93-98.

[8]YU Z， ZHANG Y， LIU Z， et al. Distributed adaptive fractional-order fault-tolerant cooperative control of networked unmanned aerial vehicles via fuzzy neural networks[J]. IET Control Theory & Applications， 2019， 13（17）： 2917-2929.

[9]ZHANG B， SUN X， LIU S， et al. Adaptive differential evolution-based distributed model predictive control for multi-UAV formation flight[J]. International Journal of Aeronautical and Space Sciences， 2020： 21（2）：538-548.

[10] YIN S， XIAO B. Tracking control of surface ships with disturbance and uncertainties rejection capability[J]. IEEE/ASME Transactions on Mechatronics， 2016， 22（3）： 1154-1162.

[11] ROVEDA L， PALLUCCA G， PEDROCCHI N， et al. Iterative learning procedure with reinforcement for high-accuracy force tracking in robotized tasks[J]. IEEE Transactions on Industrial Informatics， 2017， 14（4）： 1753-1763.

[12] GAO S， SONG R， LI Y. Cooperative control of multiple nonholonomic robots for escorting and patrolling mission based on vector field[J]. IEEE Access， 2018， 6： 41883-41891.

[13] CHOU C Y， JUANG C F. Navigation of an autonomous wheeled robot in unknown environments based on evolutionary fuzzy control[J]. Inventions， 2018， 3（1）： 3.

[14] WANG M， LUO J， YUAN J， et al. Detumbling strategy and coordination control of kinematically redundant space robot after capturing a tumbling target[J]. Nonlinear Dynamics， 2018， 92（3）： 1023-1043.

[15] YAO W， LU H， ZENG Z， et al. Distributed static and dynamic circumnavigation control with arbitrary spacings for a heterogeneous multi-robot system[J]. Journal of Intelligent & Robotic Systems， 2019， 94（3）： 883-905.

[16] LU C， WANG J， CUI X. Moving Target Tracking with Robot Based on Laser Range Finder[C]//2020 5th International Conference on Automation， Control and Robotics Engineering （CACRE）. Dalian， China： IEEE， 2020： 21-25.

[17] WANG Y， LU D， SUN C Y. Cooperative control for multi-player pursuit-evasion games with reinforcement learning[J]. Neurocomputing， 2020，412：101-114

[18] GE H， SONG Y， WU C， et al. Cooperative deep Q-learning with Q-value transfer for multi-intersection signal control[J]. IEEE Access， 2019， 7： 40797-40809.

[19] SAMPEDRO C， BAVLE H， Rodriguez-Ramos A， et al. Laser-Based Reactive Navigation for Multirotor Aerial Robots using Deep Reinforcement Learning[C]// 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems （IROS）. Madrid， Spain： IEEE， 2018.

[20] NOGUCHI Y， MAKI T. Path Planning Method Based on Artificial Potential Field and Reinforcement Learning for Intervention AUVs[C]// 2019 IEEE Symposium on  Underwater Technology （UT）. Taiwan， China： IEEE， 2019：1-6.

（責任编辑 耿金花）

收稿日期： 2021-03-12；修回日期：2022-04-10

基金项目： 国家自然科学基金（61673200）

第一作者： 韩艺琳（1997-），女，山东淄博人，硕士研究生，主要研究方向为移动多机器人编队控制。

通信作者： 杨洪勇（1967-），男，山东德州人，博士，教授，主要研究方向为移动多机器人编队控制。