快速路交通流状态突变边界提取及其演化规律

刘浩敏　曲大义　宋慧　孟奕名

摘要： 为解决快速路日益严重的拥堵现象，探讨其交通运行状态及演化规律，确定交通状态判别标准。运用交通仿真平台Vissim软件进行模拟分析，应用谱聚类分析算法精确提取交通状态突变边界，结合尖点突变理论，研究分析不同时间、位置的交通流状态。结果表明：交通流在自由流与拥堵流两种状态之间相互转化时，存在明显的突变现象。

关键词： 交通流状态；尖点突变理论；谱聚类分析算法；交通演化规律

中图分类号： U491.2文献标识码： A

Extraction of Catastrophe Boundary and Evolution of Expressway Traffic Flow State

LIU Haomin， QU Dayi， SONG Hui， MENG Yiming

Abstract：In order to solve the increasingly serious congestion of expressways， the traffic operation state and its evolution law are discussed， and the traffic state discrimination standard is determined. The traffic simulation platform VISSIM software is used for simulation analysis， and the spectral clustering analysis algorithm is used to accurately extract the abrupt boundary of traffic state. Combined with the cusp catastrophe theory， the traffic flow state at different times and locations is studied and analyzed. The results show that there is an obvious catastrophe phenomenon when the traffic flow transforms between the two states of free flow and congestion flow.

Key words： traffic flow state; cusp catastrophe theory; spectral clustering analysis algorithm; law of traffic evolution

0 引言

作为城市的交通枢纽，城市快速路在城市交通系统的运行中起着增加交通承载能力、提高道路服务水平和车辆运行效率的重要作用。城市快速路通行效率低下被大家诟病已久，控制和解决拥堵问题已经迫在眉睫。研究城市快速路交通流拥堵形成、消散的演化规律，并从时空角度探究其演变机理，可以帮助对快速路拥堵进行针对性治理，以提高城市路网通行效率。

Younes等［1］利用车联网技术对道路上的交通量、速度以及行程时间进行分析，提出一种拥堵检测算法，探究拥堵随行程时间的演化过程；Wang等［2］提出密度相关弛豫时间概念，通过研究密度分布与速度边界扰动來阐述交通流状态演化规律；Ghadami A等［3］利用发生在交通拥堵的分叉附近的动态系统中的临界减速现象，通过在转折点发生之前进行流量测量，预测分叉后交通拥堵的演化规律；Chaurasia B K等［4］结合了数据挖掘历史轨迹数据以检测和预测流量拥堵，使用轨迹聚类算法对轨迹进行聚类，从而研究道路瓶颈形成演化规律，并提出了一种减少拥堵的解决方案。

在国内，郝杰等［5］将车辆抽象成相互作用的分子，利用分子动力学分析车辆运动趋势对交通流的影响，探究其演变规律；张博等［6］结合元胞自动机模型基本理论，依据相变过程中系统流量变化趋势对参数间关联关系进行分析与讨论，可较好地描述交通流参数之间的关联演化规律；李树彬等［7］利用当前新兴的复杂网络理论结合改进的交通流仿真模型，研究了可变限速对于交通流演化的影响；胡建荣等［8］以高速公路标准路段为例，模拟车流的实时运行状态，探究不同交通流状态的判别标准和方法；林璐等［9］运用Ｋ均值聚类算法，提出在离线状态下有效判别交通状态的定量方法，从而分析其演化规律；邵子怡等［10］利用尖点突变理论平衡曲面模型，通过确定城市道路交通流状态关键的变化节点，研究交通流状态演化规律。

综上所述，可以看出国内外对于交通流状态演化规律的研究已经颇为成熟，但多是基于二维平面建立的连续交通流模型进行研究，难以解释复杂三维交通数据中不连续的突变现象，且在有限的涉及到交通流状态突变现象的相关研究中，突变区间变化长度大都通过人工设定，而后通过遍历样本集寻找变化长度内最少的数据点所对应区间作为突变区间范围，易造成其精确度与可靠性不足。本文从仿真模拟交通流数据出发，结合尖点突变理论，采用谱聚类分析算法，精准提取出交通流状态突变区间边界，从交通量、速度、占有率以及不同的时空分布等方面对城市快速路交通流状态的演化规律做出全面详细的分析。

1 交通流突变特性分析

1.1 数据采集

快速路交织区作为交通流频变路段，大量的车辆换道与交织现象使其成为常发性拥堵路段，故将其作为重点研究对象。由于实地调查数据采集的方式工作量庞大，且对于针对性问题提取代表性数据过程困难，所以采用实地调查与仿真相结合的方法进行数据采集。

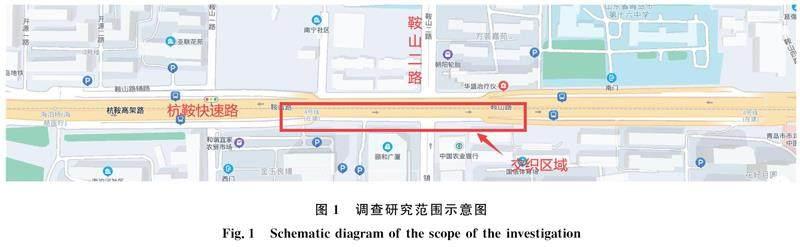
选取青岛市杭鞍快速路于鞍山二路处交织区为调查地点，采用视频检测与人工调查相结合的方法，对交织区长度、车道数、交通量等参数进行调查，调查时间段选为2021年11月22日至26日（周一到周五）每天7：00～20：00。利用交通模拟平台Vissim，将实地调查结果作为输入参数搭建仿真场景，进行数据仿真。交通仿真具体方案为：1）仿真场景：为探究交通流内部因素导致的拥堵演化规律，假设交织区不受其它路段影响，车道设置合理。快速路主路为双向6车道平直路段，长度为1 000 m，交织区长度为210 m，车道宽度3.75 m。

2）交通量：根据实际调查发现此交织区一天内交通量为1 200～3 700 pcu/h，所以标定仿真交通量为1 000～4 000 pcu/h，步长为500 pcu/h，每间隔步长仿真时长为3 600 s。

3）交织流量比：为研究交织区拥堵特性，根据《公路通行能力手册》，选取交织段为4车道时的最大交织比为0.35。

4）期望速度：依据实际调查结果，标定快速路主线期望速度为80 km/h，匝道期望速度为40 km/h。

5）数据检测：依据《公路通行能力手册》，交织区范围为汇合三角区上游0.6 m至分离三角区下游3.7 m，采用等距离分割法，在交织区范围内从分离三角区开始分内侧、中间、外侧3车道每隔5 m向上游设置数据检测点共129个检测器，并对检测断面进行依次编号，数据检测时间间隔为30 s。

6）数据输出：间隔时间内交通量、时间占有率、平均速度。

1.2 基于尖点突变理论的交通流特性分析

突变理论通过建立突变模型，探究系统中一种稳态向另一种稳态突变的内在机理。在系统的演化过程中，某个或多个因素连续变化时，可能会有某个因素发生非连续性突变，导致系统的整体态势发生改变。在突变理论的模型中，存在控制变量和状态变量，随着控制变量的连续变化，在其过程中状态变量发生突变。突变理论反映在交通流系统中，交通量和占有率作为控制变量，在交通流演化过程中，速度作为状态变量发生突变。选取交织区中间断面交通量、时间占有率、平均速度等特征指标，其相互关系如图2所示。

通过尖点突变理论对交通流演化过程进行分析，交通流状态表现出特性：1）交通流参数在自由流与拥堵流状态下分布比较集中，而两种状态之间的速度变化是不连续的，交通流状态表现出突变性；2）在自由流与拥堵流之间发生速度突变的区域，即突变区，其数据样本点极少，在此区域交通流状态非常容易发生改变，表现出突变区域的不可达性；3）在相同的交通流量下，可能呈现出两种不同的对应速度，并且两种速度所对应的交通流状态不同，即交通流存在两种稳态，呈现出双模态性。

通过对交通参数分布规律的研究分析，可以看出交通流具有明显的突变特性，与尖点突变理论有着高度的一致性，因此，利用尖点突变理论可以准确表述交通流演变规律。

2 基于谱聚类分析算法的突变边界提取

将坐标变换后的三维数据投影至奇点集方程平面，对状态变量的突变边界进行提取。传统的突变边界提取方法为基于经验确定突变长度阈值，寻找在变化阈值范围内数据点最少的区间作为突变区间，其置信度与可靠性较低。采用机器学习的方法可以有效解决上述问题，通过不断迭代动态寻找数据中心，对交通流状态进行动态聚类，从而提取突变边界，确定突变区间。

2.1 谱聚类分析算法

作为机器学习研究热点，谱聚类分析算法可以解决传统动态聚类方法中难以处理非球状簇类数据的问题［12］，对交通流状态进行高效聚类，提供更加准确可靠的结果，其具体流程：

2.3 交通特征分析

对突变边界提取结果进行分析，如图3所示，相对于自由流状态与拥堵流状态，同步流状态数据点更为稀疏，符合尖点突变理论的突变特性，其突变边界为［－22.6，0］，则坐标变换前速度边界如表1所示。

3 交通流状态演化规律解析

3.1 交通流拥堵形成规律

对尖点突变理论平衡曲面图进行分析，如图4所示，系统存在双模态性，即交通流具有自由流与拥堵流两种稳态，分别处于平衡曲面的上叶与下叶。曲面褶皱所经历的区域为不稳定区域，即同步流状态，此处既可以是连续的也可以是不连续的，表示出系统实际不可能达到的稳定状态，在演化过程中，其有可能跃迁至上叶，也可能跃迁至下叶，在交通流系统中，同步流状态既可能演变为拥堵状态，也可能演变为自由流状态。在交通流由自由流向拥堵演变时，速度从A点演化到B点突变至B1点，在拥堵消散过程中，速度在C点突变至C1点，表明系统的突变具有滞后性。在褶皱的消失处即为平衡曲面坐标原点，此时数据变换后的交通量、占有率和速度都为0，对应原始数据的最大流量、关键占有率和最优速度。

将尖点突变理论平衡曲面图投影到3个平面进行分析：1）交通量-占有率分析。在尖点突变模型中，如图5a所示，交通量分布在二、三象限，左侧为自由流，右侧为拥堵流，中间有明显的分叉区域，即同步流。在自由流状态，随着交通量增加，时间占有率也随之增加，在原点处流量达到最大；之后交通流陷入同步流状态，交通流可能呈现比自由流更小的占有率但交通量却没有自由流交通量大的情况；之后随着车辆持续输入，占有率逐渐增加，交通量逐渐减少，交通流进入拥堵状态。2）速度-占有率分析。

在交通流运行过程中，如图5b所示，系统状态处于平衡曲面上叶，即车流速度处于自由流状态，逐渐向原点靠近时，占有率逐渐增大，状态的变化过程是连续的；在到达原点时，只要控制变量发生细微改变，速度就会在原点跳跃到平衡曲面下叶，此时速度产生突变。当占有率继续增大时，系统状态稳定处于下半叶，即拥堵流状态。3）速度-交通量分析。在尖点突变模型中，对平衡曲面方程进行求导可得到关于交通量和速度的奇点集方程。如图5c所示，交通流处于自由流状态时，速度处于系统上叶，此时道路车辆以期望速度行驶，随着交通量增大，速度平滑减小，但减小幅度不大，直至到达奇点，此时速度达到最优速度；之后速度产生突变，经由同步流状态达到拥堵状态，速度与交通量同时减小。

3.2 交通流拥堵消散规律

拥堵消散是交通流演化的重要过程，其规律是研究消散控制策略的主要依据，为探究交通流拥堵消散规律，选取输入交通量为4 000～1 500pcu/h共6 h的中间断面仿真数据作为研究对象，如图6所示。

图6a～圖6f分别是每个时段（1h）采集的交通量-占有率分布关系。如图6a所示，在仿真开始时仅有极少数车辆处于自由流状态，之后迅速经过速度突变陷入拥堵，交通量几乎全部分布于拥堵流区域；而后随着输入交通量的减少，如图6b所示，交通流拥堵有所缓解，大部分车辆仍处于拥堵流状态，有少部分车辆可以达到自由流状态。随着输入交通量的进一步减少，如图6c所示，交通量与占有率的分布恢复正常水平，交通量大部分处于自由流状态。之后随着输入交通量的进一步减少，交通流状态也得到进一步优化，直至图6f，交通流分布全部处于自由流状态。

對比图6b与图6c可知，在拥堵消散过程中，交通量分布发生了明显的改变，交通流状态的突变现象仍会发生，拥堵流与自由流两种稳态之间存在明显的数据裂隙，即为同步流区域，此区域数据点非常少，验证了尖点突变理论的不可达性。同时，对比拥堵形成演化规律可知，虽然交通量与占有率两参数在拥堵形成前和拥堵消散后基本保持一致，但系统发生突变所对应的交通量与占有率有所不同，表现出尖点突变理论的滞后性。

3.3 交通流状态时空演化特性

选取输入交通量为3 000pcu/h时，外侧、中间与内侧车道所有位置断面的平均速度，从时空的角度，利用尖点突变理论对城市快速路交通流拥堵形成与消散的演化规律及其背后机理进行研究。

图7表示了快速路交通流处于不同时间、不同位置时的交通状态。在图7a中，从时间方面来看，仿真时长内外侧车道共发生13次速度突变，其中8次未演变为拥堵流，而是重新演化为自由流，5次演变为拥堵流，且同步流区域较窄，符合尖点突变特性；从空间方面来看，发生的5次拥堵中，4次发生10 m位置，即交织区出口附近，1次发生在190 m位置，即交织区入口附近，同时，剩余8次未演变为拥堵流的速度突变位置与拥堵发生位置一致。在图7b中，仿真时长内，中间车道同样发生13次速度突变，其中4次演化为拥堵流，9次重新演化为自由流；从空间上看，发生的4次拥堵全部发生在10 m位置附近，即交织区出口附近。对于内侧车道，如图7c所示，从时间来看，仿真时长内共发生9次速度突变，其中3次演化为拥堵流状态，相比于外侧与中间车道的交通流状态更优；从空间上看发生拥堵的位置同样处于交织区出口附近。

根据交通流状态时空分布对拥堵成因进行分析：1）对于外侧车道，在交织区入口处交通流仅有一次演变为交通拥堵，这是由于大部分车辆会在交织车道加速过程中寻找可插入间隙进行自由换道并入主线，这部分车辆并不会对整体交通流运行产生太大影响，只有少部分车辆会在还未完成车辆加速且未寻找到可插入间隙时进行强制

换道并入主线，使交通流速度发生突变，在入口区域形成交通瓶颈。而对于有并入主线意图的保守型交通参与者来说，在交织车道行驶过程中未寻找到可插入间隙时，会在本车道继续行驶至出口车道附近进行停车等待，寻找可插入间隙进行换道，此时会与意图驶出车辆形成博弈，从而导致交通流速度发生突变，在出口处形成交通拥堵。2）对于中间车道，由于入口车辆在驶入交织区后进行连续变道进入内侧车道现象极少发生，所以在仿真时长内入口附近未发生拥堵现象。而在出口附近，由于交织车道车辆变道进入外侧车道，此时部分外侧车道车辆会产生向内变道的意图，同时，未在上游找到可插入间隙的意图驶出的内侧车道车辆，也会在出口附近进行强制连续变道，从而阻碍中间车道交通流，所以在出口附近，相对于外侧车道，中间车道发生的速度突变更多。而且在拥堵状态下，由于外侧车道与内侧车道的共同阻碍作用，导致中间车道的拥堵持续时间更长，拥堵消散更为缓慢。3）对于内侧车道，与中间车道一样，由于在仿真时长内未出现在未找到可插入间隙的情况下进行强制连续变道进入内侧车道的车辆，所以在入口附近未出现速度突变现象。在交通量过大时，意图驶出快速路的内侧车道车辆在无法找到可插入间隙进行变道时，会在出口附近进行停车等待，强制连续变道驶出，对上游交通流产生影响，导致在出口附近产生速度突变。但由于内侧车道受外侧以及中间车道影响较小，大多数情况下仅受本车道驶出车辆影响，所以其交通流相对于另外两车道更为畅通，速度突变以及拥堵流状态出现次数更少。

4 结论

研究分析表明，城市快速路作为承担城市路网大部分压力的交通枢纽，其交通流的拥堵与否影响着整个城市的路网通行效率。快速路交通流状态的演化规律是制定拥堵治理方案、研究拥堵消散策略的关键，利用交通模拟平台Vissim仿真模拟快速路交通流运行，提取其特征参数，并在此基础上展开对快速路交通流状态演变规律的研究：在交通流状态演化过程中存在自由流与拥堵流两种比较稳定的交通流状态，而两种交通流状态之间存在明显的裂隙区域，表现出交通流演化过程中的突变性；谱聚类分析算法可以解决传统聚类算法难以处理非球状簇类数据的问题，基于网络图节点相似度有效提取交通流突变边界；在交通流拥堵形成与消散演化过程中，都会发生速度突变现象，但两种情况突变发生时所对应的交通量不同；在城市快速路中，内侧车道由于受车道减少、车辆交织等情况所造成的车辆换道影响较少，所以其车辆速度相对于外侧车道更大，交通流状态更优。

本研究只分析了单个交织区拥堵形成及消散演化规律的内因，未考虑关联路段拥堵、车道设置等因素的影响，在下一步研究中进行。

参考文献：

［1］YOUNES M B，BOUKERCHE A. A performance evaluation of an efficient traffic congestion detection protocol （ECODE） for intelligent transportation systems［J］. Ad Hoc Networks， 2015， 24： 317-336.

［2］WANG Y Q， CHU X J， ZHOU C F， et al. Evolvement law of a macroscopic traffic model accounting for density-dependent relaxation time［J］. Modern Physics Letters B， 2017， 31： 1750291.

［3］GHADAMI A， EPUREANU B I. Forecasting the onset of traffic congestions on circular roads［J］. IEEE Transactions on Intelligent Transportation Systems， 2020， 22（2）： 1196-1205.

［4］CHAURASIA B K， MANJORO W S， DHAKAR M. Traffic congestion identification and reduction［J］. Wireless Personal Communications， 2020， 114（2）： 1267-1286.

［5］郝杰，曲大义，张金磊，等.基于分子动力学的交通流特性分析方法［J］.青岛理工大学学报，2013，34（6）：87-91，124.

HAO J， QU D Y， ZHANG J L， et al. Analysis method of traffic flow characteristics based on molecular dynamics［J］. Journal of Qingdao Technological University， 2013， 34（6）： 87-91，124.

［6］张博，赵慧英.元胞自动机交通流NS模型的参数关联研究［J］.昆明理工大学学报（自然科学版），2016，41（4）：45-51.

ZHANG B， ZHAO H Y. Parameter correlation analysis and research on single-lane cellular automaton NS model［J］. Journal of Kunming University of Science and Technology （ Natural Science Edition）， 2016， 41（4）： 45-51.

［7］李樹彬，傅白白，孙涛，等.复杂网络中观交通流动态限速控制策略研究［J］.复杂系统与复杂性科学，2017，14（4）：32-42.

LI S B， FU B B， SUN T， et al. Research on complex network mesoscopic traffic flow with dynamic limit speed control strategies［J］. Complex Systems and Complexity Science， 2017， 14（4）： 32-42.

［8］胡建荣，何磊.基于尖点突变理论的高速公路交通流状态判别方法［J］.中国公路学报，2017，30（10）：137-144.

HU J R， HE L. Freeway traffic flow condition criterion method based on cusp catastrophe theory［J］. China Journal of Highway and Transport， 2017， 30（10）： 137-144.

［9］林璐，陈健，曲大义，等.基于K均值聚类算法的交通状态判别方法研究［J］.青岛理工大学学报，2019，40（4）：109-114.

LIN L， CHEN J， QU D Y， et al. Study on traffic state identification method based on K-means clustering algorithm［J］. Journal of Qingdao Technological University， 2019， 40（4）： 109-114.

［10］ 邵子怡，张林，吴昊.基于尖点突变的城市交通状态演化研究［J］.华北理工大学学报（自然科学版），2021，43（3）：74-80.

SHAO Z Y， ZHANG L， WU H. Evolution of urban traffic state based on cusp catastrophe［J］. Journal of North China University of Science and Technology （Natural Science Edition）， 2021， 43（3）： 74-80.

［11］ HALL F L. An interpretation of speed-flow-concentration relationships using catastrophe theory［J］. Transportation Research Part A： General， 1987， 21（3）： 191-201.

［12］ 耿阳李敖. 面向非规则簇结构的聚类算法研究［D］.北京：北京交通大学，2021.

GENG Y L A. Research on clustering algorithm for clusters with irregular structure［D］. Beijing： Beijing Jiaotong University， 2021.

（责任编辑 李 进）

收稿日期： 2022-01-05；修回日期：2022-05-03

基金项目： 国家自然科学基金（52272311;51678320）

第一作者： 刘浩敏（1997-），男，山西长治人，硕士研究生，主要研究方向为交通系统分析与控制优化。

通信作者： 曲大义（1973-），男，山东青岛人，博士，教授，主要研究方向为车路协同与安全控制。