面向单双频混合及中断数据周跳处理方法

曾金文，章浙涛，何秀凤，袁海军，何金鑫

面向单双频混合及中断数据周跳处理方法

曾金文，章浙涛，何秀凤，袁海军，何金鑫

（河海大学 地球科学与工程学院，南京 211100）

针对复杂环境下，传统周跳探测方法并不能取得良好的探测效果的问题，提出一种面向单双频混合及中断数据的周跳处理方法：介绍传统的无几何距离（GF）组合、墨尔本-维贝纳（MW）组合和多项式拟合法及其优势和不足；利用站间单差形式的GF组合和MW组合处理双频数据，利用改进后的多项式拟合法处理单频数据，联合3种方法克服数据中断带来的挑战，实现相对定位和实时周跳探测。实验结果表明，改进的联合探测方法比传统方法可削弱更多误差；相较于传统方法在探测率、固定率、均方根、定位偏差等精度方面都有较明显提高，其中探测修复率提高15%以上，固定率提高16.8%，复杂环境下的定位精度由分米级提升到厘米级；可为周跳处理提供参考。

周跳探测；无几何距离组合（GF）；墨尔本-维贝纳（MW）组合；多项式拟合法；单双频混合；数据中断

0 引言

利用载波相位观测值进行定位是目前全球卫星导航系统（global navigation satellite system，GNSS）的一大研究热点，然而由于障碍物遮挡、卫星信噪比过低或接收机处于相对运动状态等原因出现卫星信号失锁，导致相位观测值发生整周跳变，即周跳现象[1-2]。周跳一旦发生会持续影响后续历元的模糊度固定，最终影响定位结果[3]。准确探测并修复周跳是载波相位精确定位的前提。然而在一些低成本接收机中，观测值以单双频混合形式出现；在观测条件较差时，观测值出现缺失甚至中断，这对周跳的探测和修复工作是一个挑战。

目前，常见的周跳探测方法有基于单频的高次差法[4]、多项式拟合（polynomial fitting，PF）法[5-6]和单频码相组合法[7]等；基于双频的无几何距离（geometry-free，GF）组合法[8-9]、墨尔本-维贝纳（Melbourne-Wübbena，MW）组合法[10]和图尔博·埃迪特（TurboEdit）法[11]等。其中，高次差法无法实现实时探测，而单频码相组合法依赖伪距精度有限；GF组合法和MW组合法都有不敏感周跳，一般须组合使用。如今，低成本接收机使用普遍，在复杂条件下，相位更容易发生周跳，传统周跳探测方法并不能取得良好的探测效果。

本文面向单双频混合及中断数据，基于相对定位模式，联合站间单差形式的GF、MW组合法和多项式拟合法分别对双频和单频数据实现实时周跳探测。

1 周跳探测方法

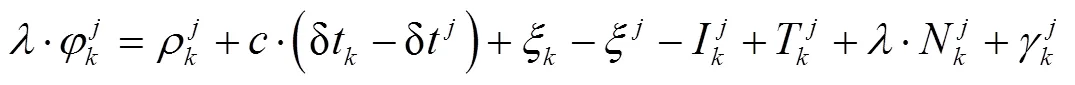
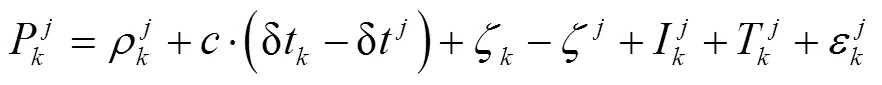
1.1 GF组合法和MW组合法

1.1.1 GF组合法

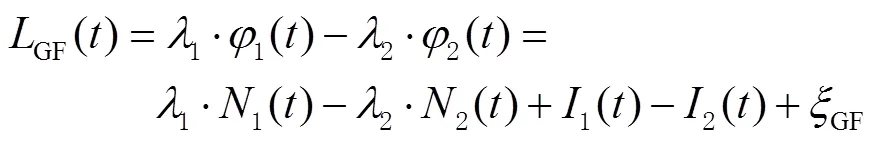
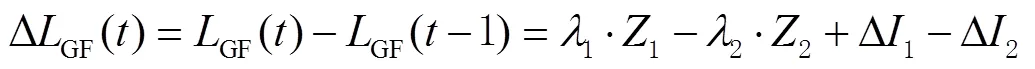
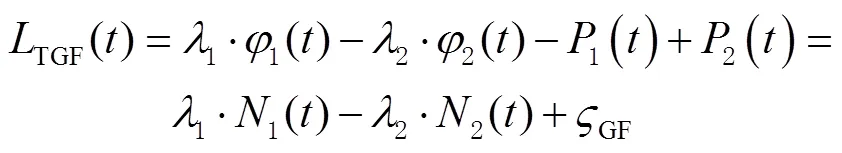
该组合观测值虽然消除了电离层延迟影响，但由于引入码伪距精度有所下降。

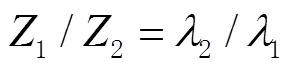
1.1.2 MW组合法

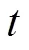
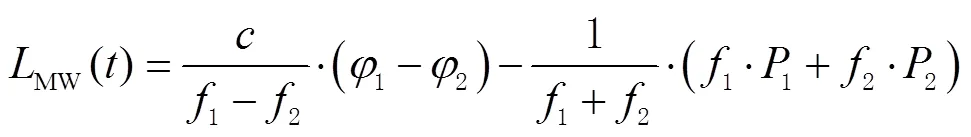
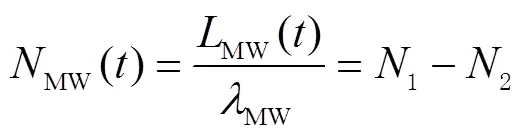
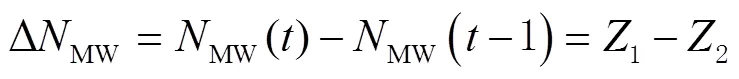
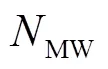
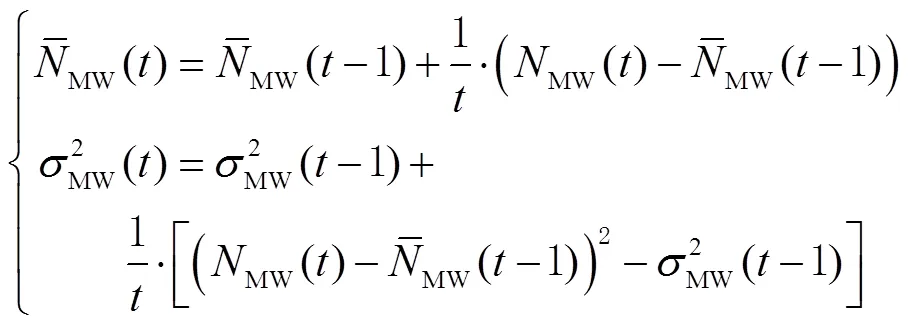
若满足以下2个条件，即：

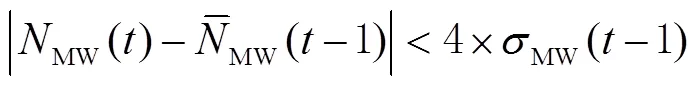
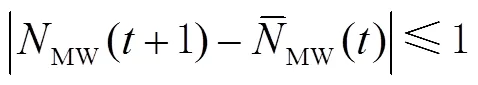
则认为当前历元没有发生周跳，可由式（9）持续更新模糊度均值和方差。若只满足式（11），则认为发生周跳；若式（10）、式（11）均不满足，则认为当前历元出现粗差。

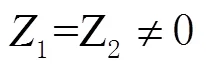
1.2 多项式拟合法

多项式拟合法的数学模型可表示为

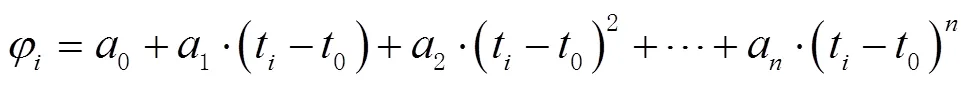
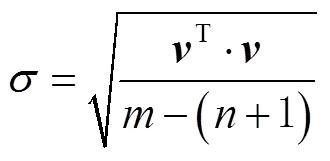
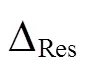
多项式拟合法探测能力一般取决于拟合中误差的大小，对小周跳探测能力有限。理论上，最小二乘具有无偏性，但是不具备抗差性。一旦有含周跳相位参与拟合或周跳修复不正确，就会因为连续外推导致误差的累积；且传统方法在数据中断时间较长时模型误差累积会过大，周跳探测可靠性不强。

2 联合GF、MW和多项式拟合法的改进方法

相对定位模式下，GNSS数据是基于差分观测值处理的。差分观测值有着非差观测值没有的独特优势，它可消除或减弱一些具有系统性误差的影响，如卫星轨道误差、钟差和大气折射误差等。

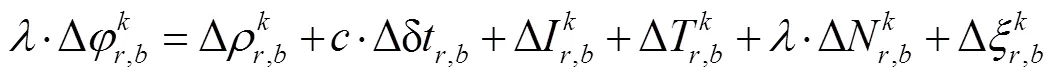
在短基线中，2站间距离较近，大气较类似，各类误差具有一定的相关性；如相位观测值中电离层、对流层延迟差分后能被削弱；各系统性误差，如轨道误差、钟差等，差分后也可被削弱甚至消除。特别地，在相对定位中，当基准站和流动站相同卫星同一频率发生相同的周跳时，差分后也得以消除。

由于GF、MW组合各自的缺陷，在实际应用中大多组合使用，如应用广泛的TurboEdit法。然而传统的TurboEdit无法实现实时探测和分离周跳参数，且对于单频卫星该方法失效。故本文基于TurboEdit方法，利用站间单差观测值作为基本观测量，改进MW+GF组合法，并联合多项式拟合法处理单频卫星周跳。

2.1 站间单差形式GF+MW方法

2.1.1 站间单差形式GF组合

站间单差形式的GF组合能大大地削弱电离层的影响，弥补了不能较好适用高采样率情形的不足，忽略微小项其数学模型为

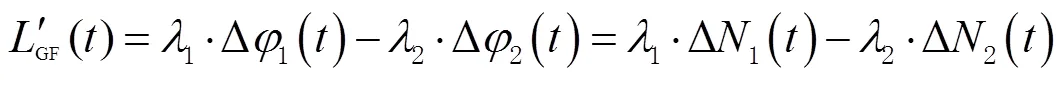
为验证站间单差形式对于电离层延迟等误差影响的削弱和相对于非差形式的优势，使用带扼流圈天线的大地测量型接收机P5，天线为CHCNAV制造的AT312，2021-11-04在开放天空无遮挡环境下采集1 d采样率为1 s的数据进行实验，当日Kp指数为40-，如图1所示，当天电离层异常活跃。

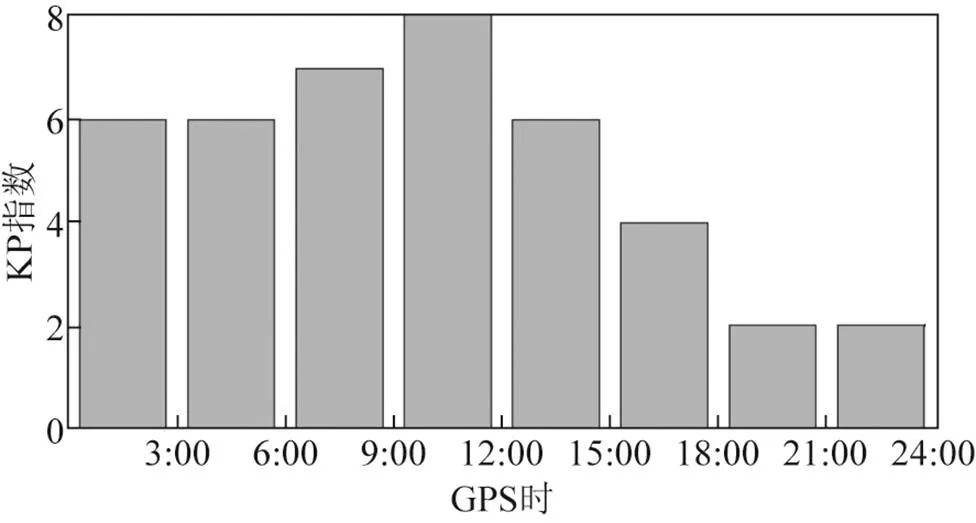
图1 2021-11-04的Kp指数图

将观测数据裁剪为5、30和60 s，由式（5）计算非差、单差形式的GF组合时间差分量，对比在电离层活跃当日的变化，如图2所示。

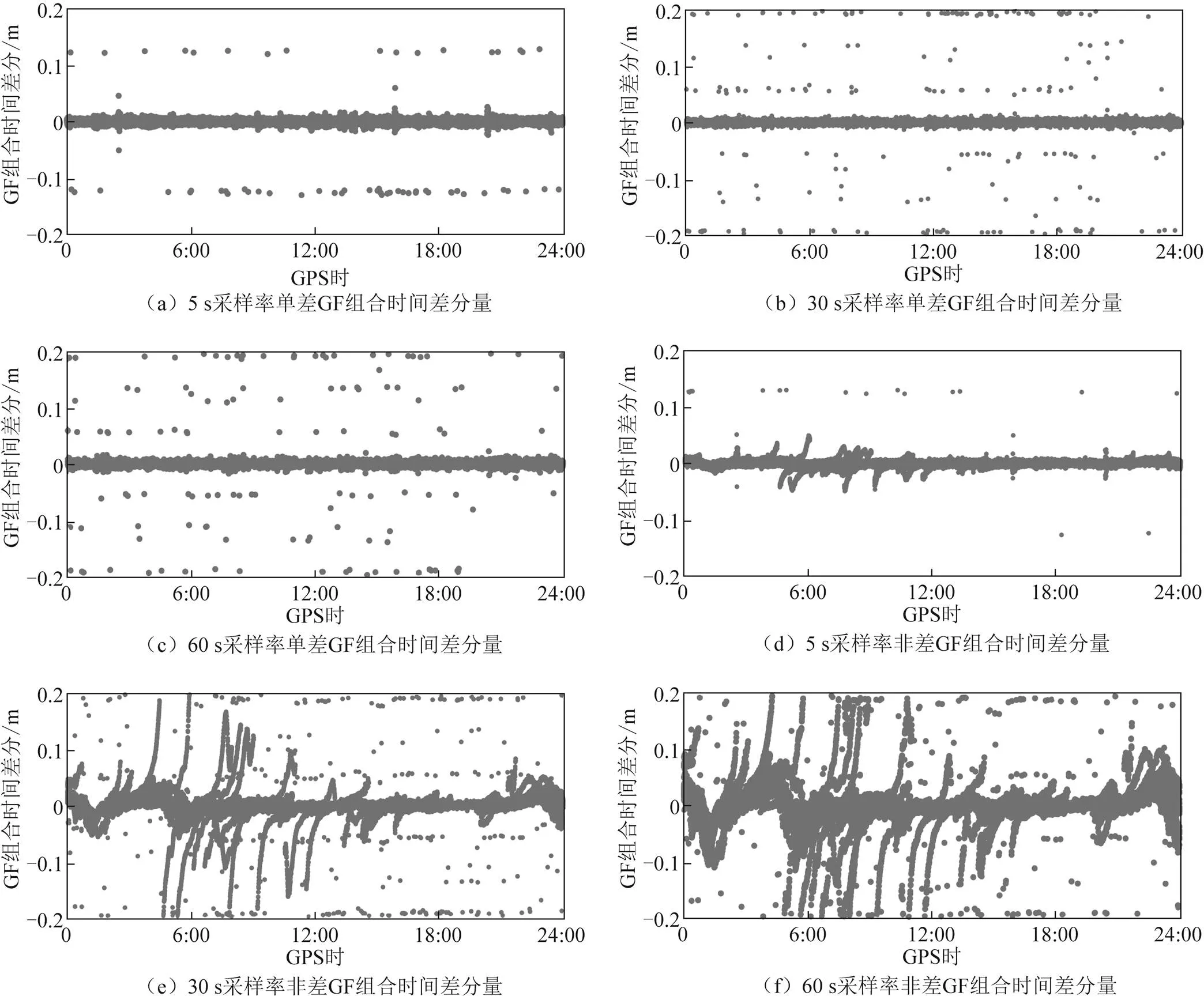
图2 不同采样率下非差与单差GF组合时间差分量

由图2可知，非差形式的GF组合受电离层影响严重；TurboEdit中单差GF组合在不同采样率下虽然克服了电离层延迟影响，但精度大大下降；站间单差形式的GF组合有效地削弱了电离层延迟的影响并保持了相位精度，在相对定位中具有优势。

2.1.2 站间单差形式MW组合法

类似地，站间单差形式的MW组合法数学模型为

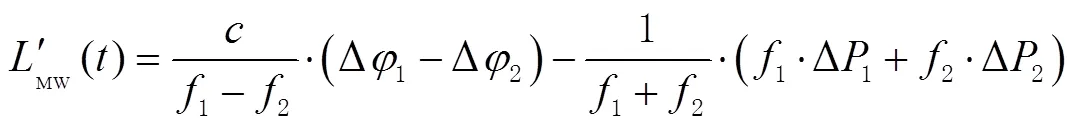
类似TurboEdit中的MW组合，该方法无法实时探测；为满足实时周跳探测的需要，对判断周跳的条件也做了改进。当满足

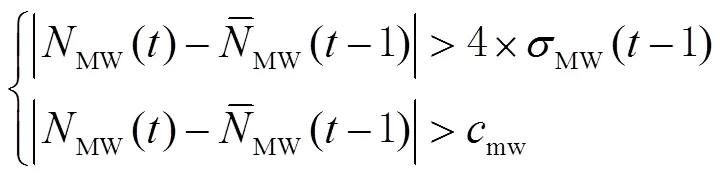
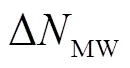
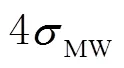
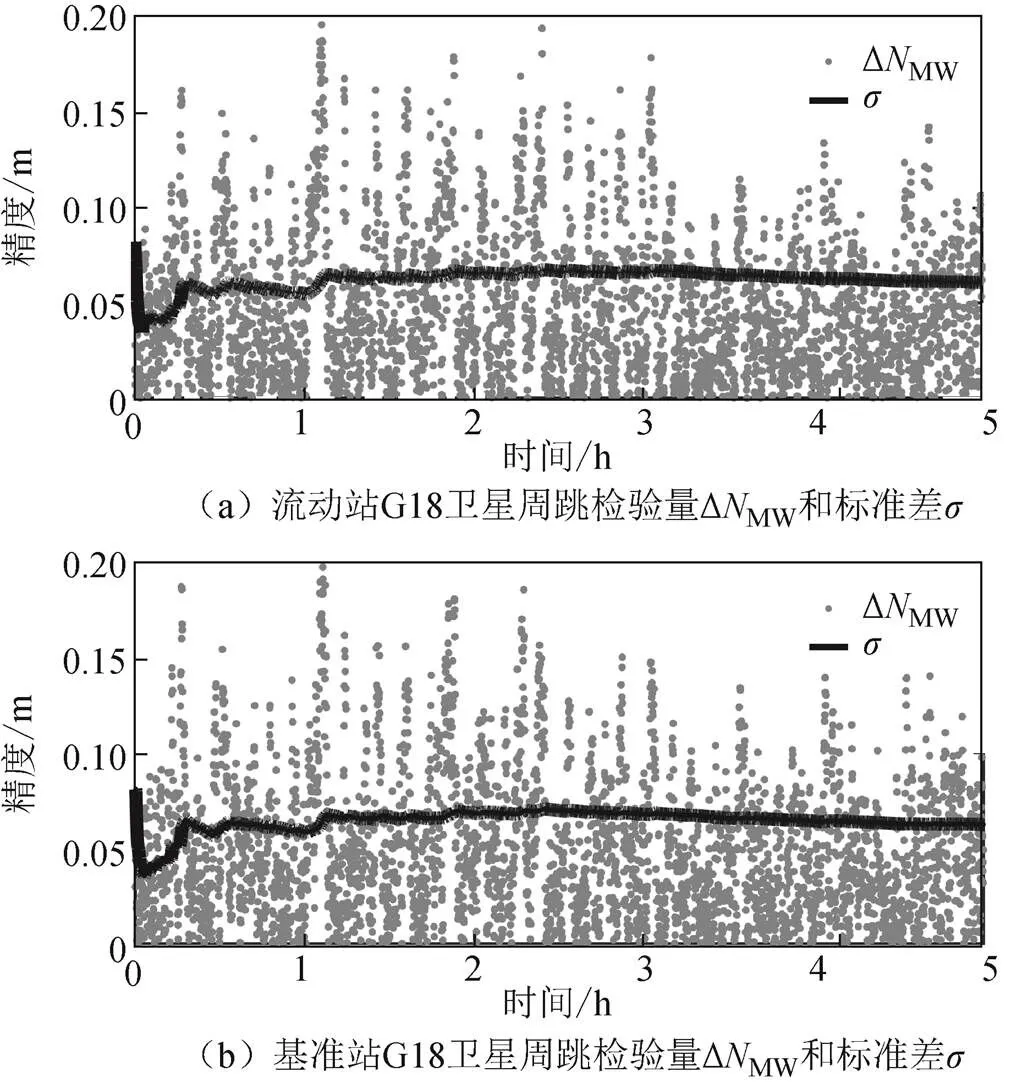
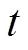
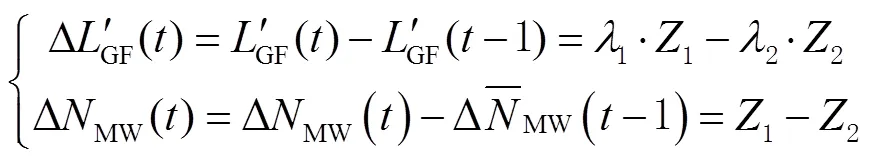
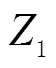
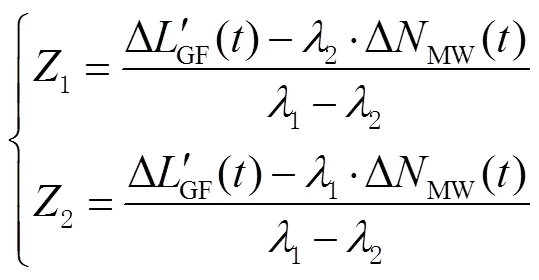
双频条件下，用上述联合方法探测周跳，当为单频卫星或观测值数据缺失中断无法使用双频方法时，则用改进的多项式拟合法。

2.2 改进的多项式拟合法

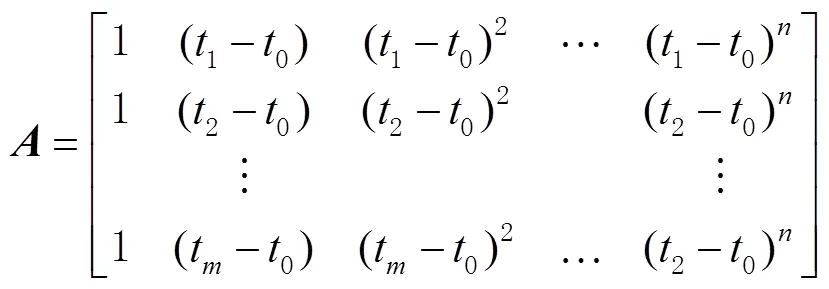
使用与2.1节同类型的接收机和天线，相同环境下在2021-11-07采集1 s采样率为5 h的理想无周跳数据进行多项式拟合法实验。同1.2节，若拟合多项式阶数为，拟合观测值个数，即拟合窗口大小为，分别以、和进行拟合实验，得到3组多项式法拟合残差和拟合中误差；当存在一个最小值，使得99%的统计数据小于，便视为该条件下的阈值，即拟合残差阈值，拟合中误差阈值。得到拟合阶数=2、3和4的多项式拟合法不同采样率阈值，如图4所示。

经典的多项式拟合法周跳发生判断依据一般为是残差大于3或4倍中误差；然而实验中同一拟合弧段的残差中误差比可达到10倍以上，同时残差小于1个周期。由上，当多项式拟合法满足不同采样率下阈值

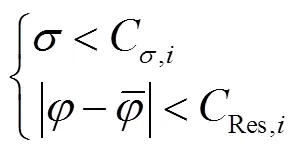
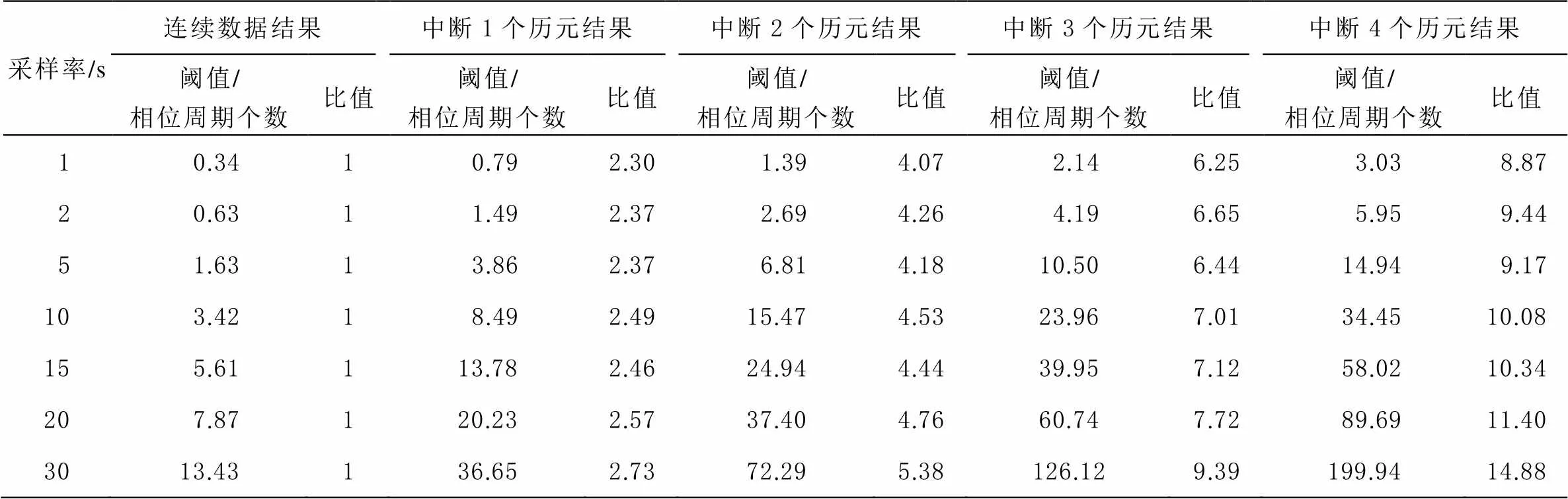
表1 各采样率下多项式阈值统计

对比连续数据，不同采样率观测数据中断历元数相同时，其阈值与连续数据阈值的比值大致相当，随着采样间隔增大而略有增大。例如当观测数据缺失2个历元时，1～20 s阈值相对于连续数据阈值增大4到5倍；当缺失历元越多，该比值越大且越不稳定，探测能力就越弱，可靠性太差。

故本文采用的2阶4窗口多项式模型，在缺失历元多于5个历元及以上时，不再使用多项式拟合，改为重新初始化拟合窗口并重新估计模糊度参数；小于5个历元时，缺失历元个数分别为0、1、2、4时，新阈值基于连续数据阈值放大倍数分别为1、2.5、4.5、7。

综上，顾及复杂环境下阈值放大常数，面向带有中断及缺失数据，设置动态阈值的周跳判断条件为

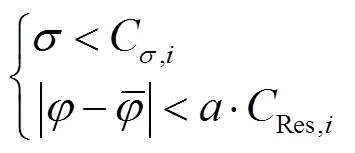
当满足式（22）上下二式时，认为没有发生周跳；满足上式而不满足下式，则认为发生周跳；若不满足上式，则认为拟合有误。该方法在观测值中断缺失历元越少或采样间隔越小时，可靠性越强，精度越高。

3 实验与结果分析

3.1 仿真模拟实验分析

3.1.1 实验数据

为验证联合GF、MW和多项式拟合法的改进方法的有效性，实验使用带扼流圈的P5接收机，天线为AT312，在无遮挡的开阔环境下，于2020-12-30以5 s的采样率，采集全球定位系统（global positioning system，GPS）L1C、GPS L2W和北斗卫星导航系统（BeiDou navigation satellite system，BDS）B1I、BDS B2I的观测数据共5 h，模拟单双频混合数据，对3种方法进行测试。

3.1.2 仿真模拟实验

在该数据中加入的周跳及根据第2节得到相应周跳检验量如表2所示。

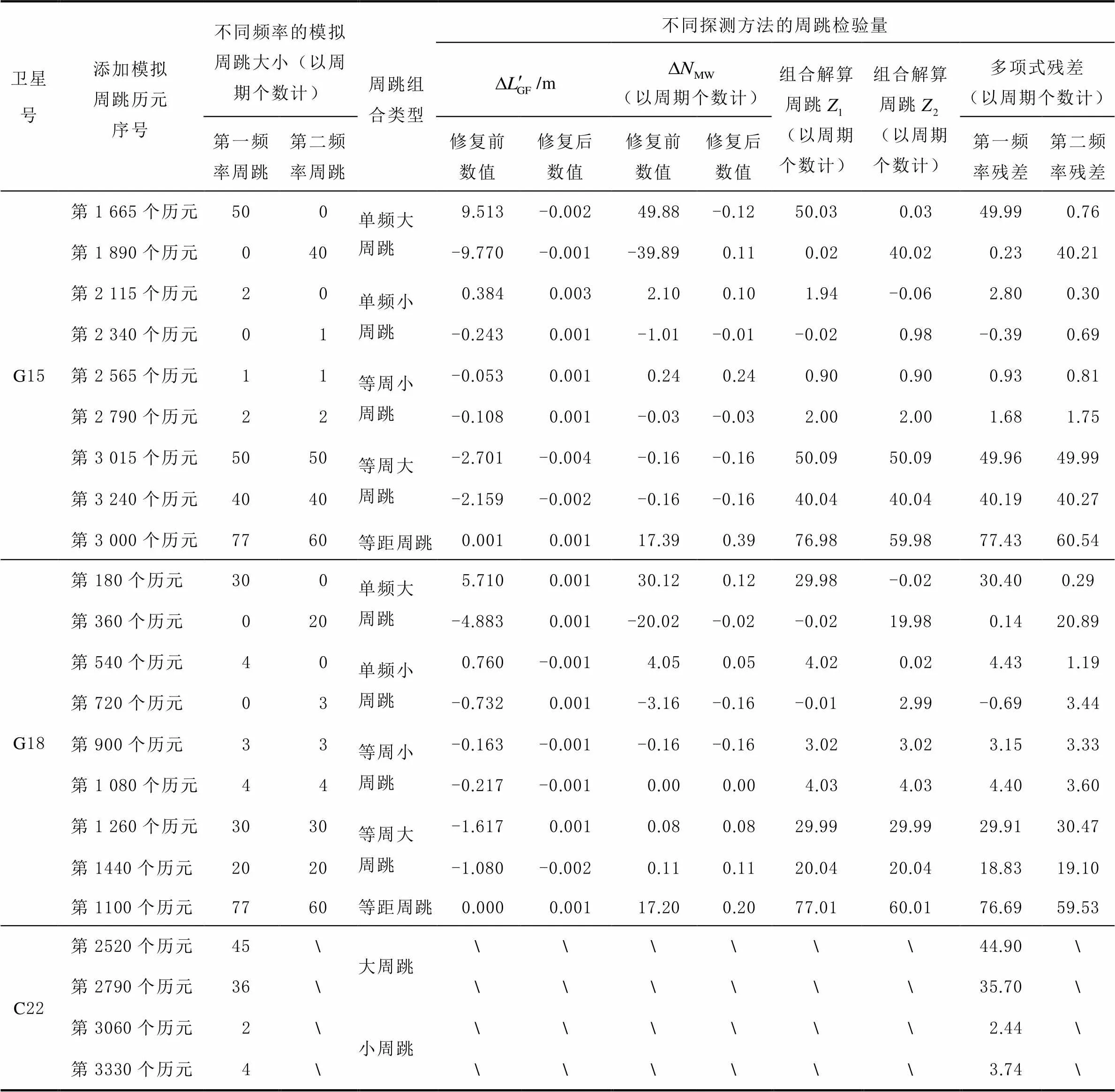
表2 模拟周跳及周跳检验量

由表2可知，联合GF和MW组合解算的双频周跳与模拟周跳大小基本一致，修复后的组合观测值均小于周跳探测阈值；多项式拟合法探测的周跳的精度不如联合GF和MW组合周跳解算精度，不过填补了单频周跳探测空白，在阈值设为1.63个周期的周跳时，大部分周跳能被探测。联合解算方法弥补了双频GF/MW组合不能分离周跳频率及大小，和无法处理单频周跳的缺陷，探测率相比单个方法提高了15%以上。

3.2 实测数据实验

3.2.1 实验数据

在四川省通江县大通江滑坡监测工程环境下，使用2台型号为HG-BX-RAG360的低成本形变监测接收机，参考站架设在开阔稳定条件下，流动站架设地具有高山峡谷和植被遮挡条件。于2021-04-14，以5 s的采样率，采集BDS/GPS双系统单双频混合（L1C/L2X和B1I/B2I）的滑坡监测数据。平均卫星数为15.5，其天空图如图5所示。由图5可知，环境遮挡较严重，信噪比变化大，其噪声水平较大，观测值质量不佳。实验使用的部分数据缺失严重。卫星和整体完整率情况如图6和表3所示，该监测数据完整性较差，卫星观测相位数据单频占比达30%～45%，单纯的双频周跳探测方法并不能满足该环境下周跳探测需求。

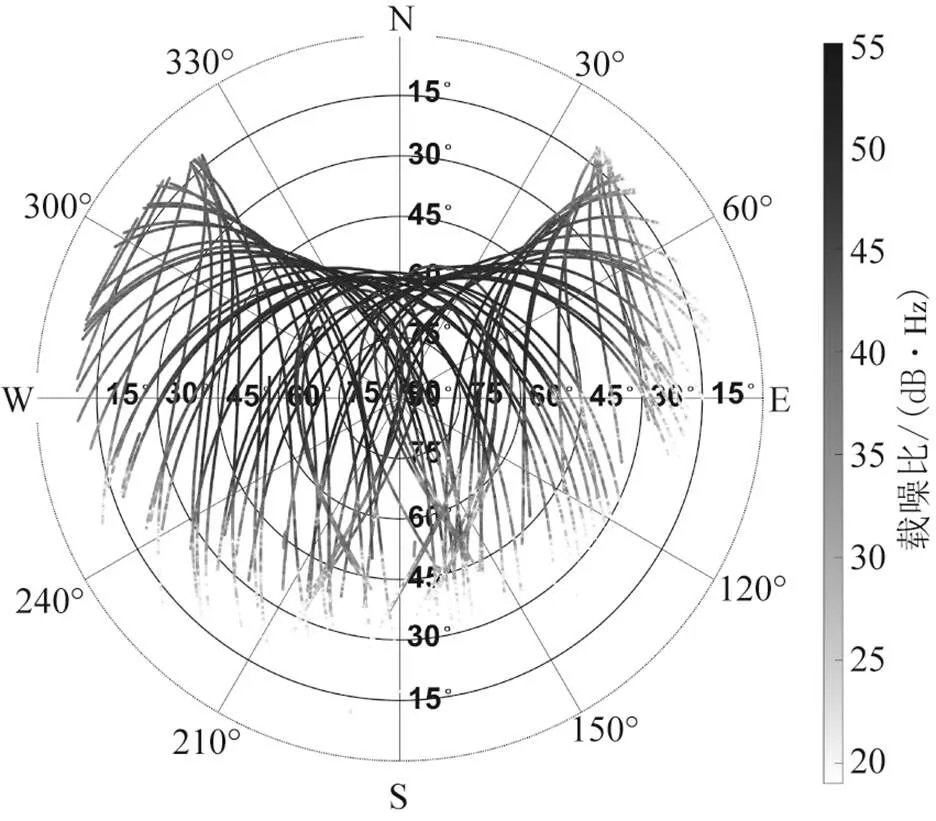
图5 流动站天空图

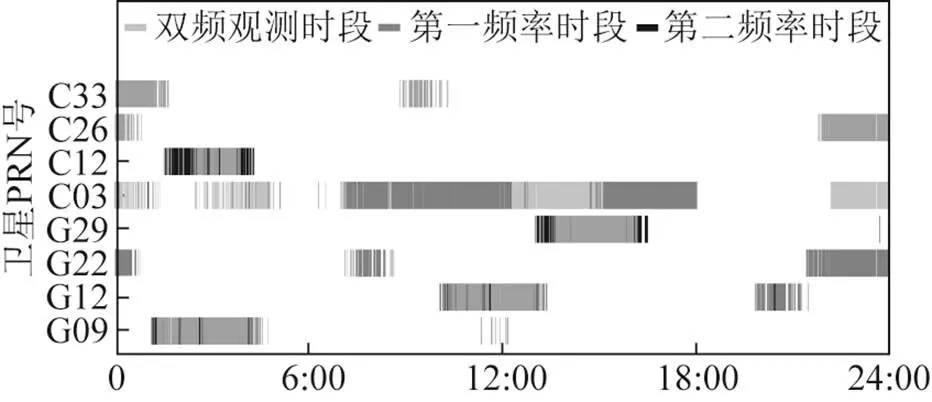
图6 实验数据部分卫星完整率情况

表3 数据完整率统计 %

3.2.2 实测数据实验

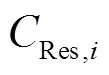
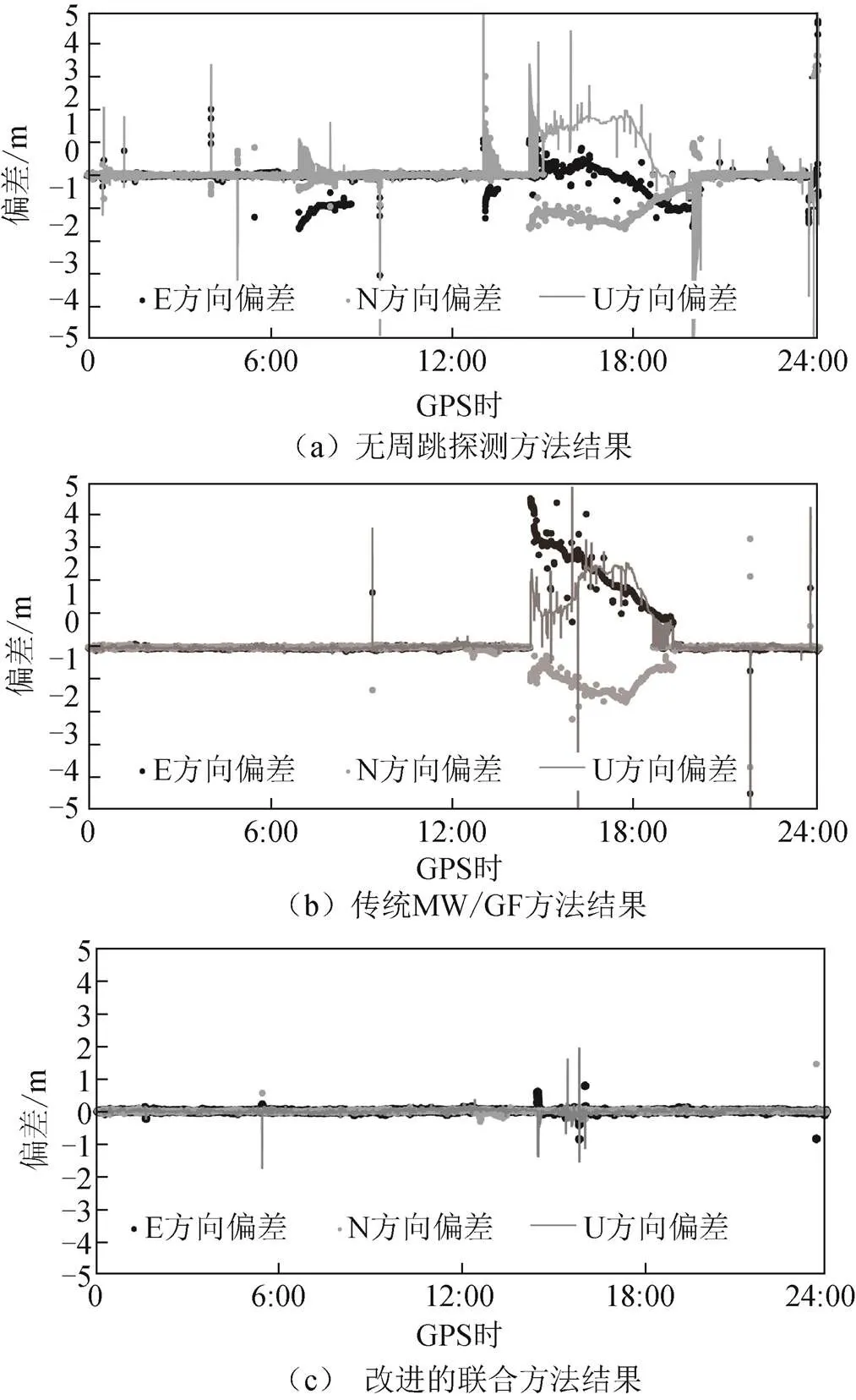
图7 不同方法解算定位偏差

由图7可知，就定位偏差来看，相对于无周跳处理方法，传统非差MW/GF组合方法在双频周跳处理有一定效果，然而对存在于单频点卫星的相位周跳，特别是大周跳，无法消除其影响；改进的多项式拟合法对周跳的敏感程度有一定提升，联合单差MW/GF方法，基本能消除大部分周跳影响。实验统计了不同方法的固定率和E、N、U方向的均方根（root mean square，RMS）和平均偏差（Bias），其结果如表4所示。

表4 不同周跳探测方法的精度指标 m

由表4可知：没有周跳处理的定位结果固定率最低，MW/GF组合有一定提升，改进的联合方法最高，达92.9%；然而，就平均定位偏差和均方根来看，传统的GF、MW方法在此类观测数据上适用性并不强，表现为均方根和定位偏差偏大；改进的联合方法不论从固定率还是偏差、RMS都是整体最优，联合方法一定程度上克服了各自缺陷，结合了各方法优点，E和N方向平均偏差在2 cm左右，U方向也在5 cm以内。

4 结束语

针对联合GF、MW和对多项式拟合法对单双频混合和中断数据的周跳处理进行研究，本文得到以下结论：

1）站间单差形式的GF和MW组合相比非差的GF和MW组合削弱了更多误差项影响，更适用于相对定位模式；不同采样率下站间单差形式GF组合误差相对更小；站间单差形式的MW组合表现得比非差形式更加稳定，削弱了伪距影响，精度有所提高；联合解算周跳参数方法能分离周跳发生大小和频率。

2）传统多项式拟合法用预测值连续外推拟合会积累模型误差，特别是在数据中断时间长的历元，外推值误差大大增加，需要依据数据中断时间动态修改多项式拟合判断阈值；多项式拟合并不适用于采样间隔过大，数据缺失中断时间过长的预测。

3）本文改进的联合方法对比传统的GF/MW组合法和在复杂环境下的单双频混合数据上有最佳的效果，其固定率、均方根和定位偏差最佳。

[1] 王耀鼎, 刘文祥, 王飞雪. 基于多项式拟合法北斗三频周跳探测改进技术研究[J]. 全球定位系统, 2016, 41(5): 79-83.

[2] 陈逸伦, 郝金明, 于合理, 等.一种改进的星载GPS周跳探测与修复方法[J]. 全球定位系统, 2017, 42(2): 32-36.

[3] 夏思琦, 于先文. 一种无盲点GNSS三频组合周跳探测与修复方法[J]. 测绘科学, 2020, 45(7): 62-69.

[4] DING Y, ZHU H, ZHONG S, et al. L2-L∞ filtering for Markovian jump systems with time-varying delays and partly unknown transition probabilities[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(7): 3070-3081.

[5] 罗峰, 姚宜斌, 宋伟伟. 综合利用多项式拟合和载波相位变化率探测单频GPS周跳[J]. 全球定位系统, 2007, 32(5): 9-13.

[6] 李明, 高星伟, 徐爱功. 一种改进的周跳多项式拟合方法[J]. 测绘科学, 2008, 33 (4): 82-83, 99.

[7] 张成军, 许其凤, 李作虎. 对伪距/相位组合量探测与修复周跳算法的改进[J]. 测绘学报, 2009, 38(5): 402-407.

[8] Goad C C. Precise positioning with the GPS[J]. Applied Geodesy, 1987, 12: 17-30.

[9] 陈猛, 李建文, 陈星宇, 等. 联合MW组合法及改进电离层残差法的周跳探测新方法[J]. 全球定位系统, 2016, 41(4): 39-42.

[10] MELBOURNE W G. The case for ranging in GPS-based geodetic systems[J]. See Goad1995, 21(5): 343-386.

[11] WÜBBENA G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements[C]//Anon. Proceedings of First International Symposium on Precise Position with GPS. Rockville, Maryland, 1985: 403-412.

[12] LI B, ZHANG Z, SHEN Y, et al. A procedure for the significance testing of unmodeled errors in GNSS observations[J]. Journal of Geodesy, 2018, 92(10): 1171-1186.

[13] 黎蕾蕾, 杨盛, 丁学文, 等. 一种INS辅助的PPP周跳探测方法[J]. 测绘学报, 2018, 47(11): 1457-1465.

[14] 卢祥, 何骞, 刁锦通. 周跳探测中一种改进的电离层残差法[J]. 测绘工程, 2016, 25(1): 17-20.

[15] 李博峰, 秦园阳, 陈广鄂. 基于无几何电离层滤波模型的北斗三号系统相位周跳与中断修复方法[J]. 测绘学报, 2022, 51(4): 501-510.

[16] 李成钢, 左翔, 史小雨. 一种精密单点定位GF组合周跳探测方法[J]. 导航定位学报, 2017, 5(4): 6-9.

[17] 刘柳, 吕志伟, 戴琦, 等. 利用三频数据组合探测不敏感周跳[J]. 武汉大学学报(信息科学版), 2019, 44(3): 392-397.

[18] 蔡成林, 沈文波, 曾武陵, 等. 多普勒积分重构与STPIR联合周跳探测与修复[J]. 测绘学报, 2021, 50(2):160-168.

[19] 崔立鲁, 张涌, 安家春. 超宽巷组合辅助电离层残差法北斗周跳探测与修复[J]. 科学技术与工程, 2018, 18(15): 1-5.

[20] 夏磊, 赖祖龙, 梅长松, 等. 实时周跳探测与修复的TurboEdit历元差优化算法[J]. 武汉大学学报(信息科学版), 2021, 46(6): 920-927.

[21] 方荣新, 施闯, 魏娜, 等. GPS数据质量控制中实时周跳探测研究[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1094-1097.

[22] 王金龙, 兰孝奇, 高奋生. 多项式拟合法和电离层残差法联合探测与修复周跳[J]. 测绘工程, 2013, 22(1): 25-27.

[23] 石双忠, 冯尊德. 利用多项式拟合预测残差修正法估算周跳值[J]. 测绘科学, 2013, 38(1): 33-35.

Cycle slip processing method for mixed single and dual frequencies and data gaps

ZENG Jinwen, ZHANG Zhetao, HE Xiufeng, YUAN Haijun, HE Jinxin

（School of Earth Science and Engineering, Hohai University, Nanjing 211100, China）

Aiming at the problem that the traditional cycle slip detection method can not achieve good detection effects, the paper proposed a cycle slip processing method for mixed single and dual frequencies and data gaps: the traditional geometry-free (GF), Melbourne-Wübbena (MW) combination and polynomial fitting method were introduced, and the advantages and disadvantages of each method were evaluated; then the GF combination in the form of single difference between stations and MW combination were used to process the dual-frequency data, and the improved polynomial fitting method was used to process the single-frequency data, thus the three methods were combined to overcome the challenge of data gaps and realize relative positioning and real-time cycle slip detection. Experimental result showed that compared with the traditional method, the proposed combined detection method could weaken more errors, and improve the accuracy of detection rate, fixed rate, root mean square, positioning deviation and so on, among which the detection and repair rate would increase by more than 15%, and the fixed rate by 16.8%, in addition, the positioning accuracy under complex environments could be improved from decimeter level to centimeter level, which could provide a reference for cycle slip processing.

cycle slip detection; geometry-free (GF) combination; Melbourne-Wübbena (MW) combination; polynomial fitting method; mixed single and dual frequencies; data gap

P228

A

2095-4999(2023)02-0061-10

曾金文, 章浙涛, 何秀凤, 等. 面向单双频混合及中断数据周跳处理方法[J]. 导航定位学报, 2023, 11(2): 61-70.（ZENG Jinwen, ZHANG Zhetao, HE Xiufeng, et al. Cycle slip processing method for mixed single and dual frequencies and data gaps[J]. Journal of Navigation and Positioning, 2023, 11(2): 61-70.）DOI:10.16547/j.cnki.10-1096.20230207.

2022-06-17

国家自然科学基金项目（41830110，42004014）；江苏省自然科学基金青年基金(BK20200530）; 中国博士后科学基金资助项目（2020M671324）；江苏省博士后科研资助计划项目（2020Z412）。

曾金文（1998—），男，江西崇义县人，硕士研究生，研究方向为GNSS精密定位和数据处理。

何秀凤（1962—），女，江苏泰州人，博士，教授，研究方向为卫星导航与定位、变形监测技术、InSAR和GPS集成技术。