不同缓冲（能力）跑鞋对跑者膝、踝关节局部动态稳定性的影响

相亮亮 ，梅齐昌 ，李建设Justin Fernandez ，顾耀东 *

跑步由于没有场地要求、技术门槛低并且具有愉悦身心、降低体脂率和减少慢性疾病患病风险等优点，逐渐发展成为深受人们喜爱的运动项目（郝琦 等，2012；梅齐昌 等，2019；张新 等，2016）。然而，由于跑步是一种长期重复性的周期运动，并且足部在支撑期受到的地面反作用力是自身体质量的1.5～3.0 倍，其相对应的损伤（特别是下肢损伤）也十分常见（傅维杰 等，2013； Lieberman et al.，2010； Van Gent et al.，2007）。Van Gent 等（2007）研究发现，在某一特定年份中79%的跑者报告经历过跑步相关的下肢运动损伤。针对跑步高运动损伤风险的特征，不同类型的跑鞋设计用于预防跑步相关损伤（Sinclair et al.，2016）。目前运动鞋具技术虽有所发展，但跑步相关的损伤并未得到明显改善（Lopes et al.，2012）。关于跑鞋的设计及其是否能够对跑步生物力学产生影响，降低跑步相关的运动损伤仍未有定论（Agresta et al.，2018）。

近年来，裸足跑的相关研究引起了足部生物力学学者的关注（Li，2017）。Lieberman 等（2012）研究发现，与穿着传统跑鞋跑步相比，裸足跑更有利于发展足部肌肉、维持足部纵弓的三角结构，且长期裸足跑能够有效提高足弓刚度。极简跑鞋的设计灵感源自裸足跑，具有中底厚度薄或无中底、掌跟差小、灵活性高及重量轻等特点，其设计目的是在跑步着地时提供更少足部支撑以达到锻炼足部肌肉和内侧纵弓的目的，同时避免裸足跑导致的擦伤、挫伤等损伤风险（Hannigan et al.，2020；Ridge et al.，2019）。但也有研究认为，极简跑鞋较传统跑鞋增加了跑步相关的损伤风险（Ryan et al.，2014）。因此，极简跑鞋对跑者产生影响的生物力学机制和结果仍然存在争议（Becker et al.，2020）。

极致缓震跑鞋是与极简跑鞋完全不同的跑鞋，具有掌跟差（heel-toe drop）小（≤10 mm）、中底厚（＞30 mm）和减震效果好等特点（张希妮 等，2019；Chan et al.，2018； Pollard et al.，2018）。目前，极致缓震跑鞋相关研究主要聚焦于跑鞋是否具有其所宣传的缓冲减震作用以及与极简跑鞋相比是否在降低跑步着地时的地面冲击力上更有优势（Agresta et al.，2018； Sinclair，2017）。Sinclair 等（2016）通过对极致缓震跑鞋和极简跑鞋进行下肢生物力学研究发现，极简跑鞋着地时的瞬时负载率、胫骨加速度和胫骨内旋峰值均大于极致缓震跑鞋。也有研究发现，相比于极简跑鞋，穿着极致缓震跑鞋的跑者5 km 跑后着地的冲击力和负载率均增加（Pollard et al.，2018）。但目前极致缓震跑鞋的相关研究十分有限，尚不清楚其缓冲减震效果是否能够达到有效降低跑步损伤风险的目的（Hannigan et al.，2020）。

局部动态稳定性是指人体神经肌肉系统减弱系统外部干扰的能力，即系统对细微扰动的敏感度（Dingwell et al.，2006）。通过局部动态稳定性分析非线性时间序列数据，能够将捕获到的对运动非常小的干扰（如步幅与步幅之间的波动对步态的干扰）量化为多个时刻的运动轨迹分散度（Horst，1987）。因此，与传统分析方法相比，能够对运动系统时间波动的动态平衡提供更为全面、准确的分析（Dingwell et al.，2001）。Lyapunov 指数是描述时间序列数据所生成的相空间中2 个极其相近的初值（两点）所产生的轨迹，随时间（迭代次数）推移按指数方式分散或收敛的平均变化率（张勇 等，2009）。局部动态稳定性可以通过计算最大有限时间的Lyapunov 指数进行评估（吕金虎 等，2002）。最大Lyapunov 指数越大，局部动态稳定性越差（Bruijn et al.，2013； Mehdizadeh，2018； Terrier et al.，2013）。Manor 等（2009）利用有限时间最大Lyapunov 指数评估运动变异率，发现最大Lyapunov 指数增大时，动态系统对于小尺度波动干扰的敏感性增加，致使局部不稳定性增加。

传统的步态变异性和稳定性测量往往仅测试下肢关节角度的复步周期变异程度，但跑步的动态平衡测试并非单纯空间上的复步步态稳定性测试，而是包括步态与步态间的差异性以及随时间延长而不断改变的运动学的变化性（England et al.，2007）。通过局部动态稳定性分析能够从运动时间控制方面评估跑步过程中的动态平衡变化（李立 等，2014；Ekizos et al.，2017）。本研究针对极致减震跑鞋和极简跑鞋进行局部动态稳定性分析，通过对比极简跑鞋和极致缓震跑鞋与传统跑鞋：1）阐述跑步运动表现及相关损伤机理的生物力学研究理论；2）探究3 类跑鞋在跑步过程中下肢关节峰值合加速度以及局部动态稳定性的差异，为跑者鞋具选择提供建议。

1 研究对象与方法

1.1 研究对象

通过统计学软件G*Power 3.1.9.4 进行样本量分析，输入参数选择效应量为0.5，显著性水平α=0.05，组数为3 组，检验效能为0.8，确定本研究的样本量为12（Faul et al.，2007）。因此，本研究选取12 名男性业余跑者作为受试者［年龄：（26.3±1.1） 岁，身高：（1.75±0.02） m，体质 量：（63.3±2.7） kg，BMI：（20.8±1.3） kg/m2，跑龄≥3 年］，所有受试者在日常生活中均有跑步习惯，平均2～3 次/周，每次跑步平均距离≥5 km。受试者均以右腿为优势腿，在中低速的跑步速度下均采用后跟着地模式（通过观察受试者在跑步机上以自选舒适速度跑步时的着地模式确定），无神经系统相关疾病且近半年未发生过下肢相关损伤（Bertelsen et al.，2013）。实验前告知受试者本研究的实验方案、过程及目的，并签署知情同意书。

1.2 实验用鞋

本研究的实验用跑鞋包括极致缓震跑鞋、传统跑鞋和极简跑鞋（图1）。传统跑鞋和极致缓震跑鞋的中底均由乙烯-醋酸乙烯酯聚合物（ethylene-vinyl acetate，EVA）材料制成，极简跑鞋无中底。3 类跑鞋的外底均由橡胶材料制成，鞋码为41～43 欧码。极简跑鞋的后跟高度为8 mm，前足和后跟的掌跟差为0 mm；传统跑鞋的后跟高度为33 mm，前足和后跟的掌跟差为12 mm；极致缓震跑鞋的后跟高度为46 mm，前足和后跟的掌跟差为10 mm。

图1 极致缓震跑鞋（A）、传统跑鞋（B）和极简跑鞋（C）Figure 1.Maximalist Running Shoes （A），Conventional Running Shoes （B），and Minimalist Running Shoes （C）

1.3 最大Lyapunov指数计算原理

最大Lyapunov 指数通过测量状态空间相邻点的指数发散速率，进而量化系统的局部动态稳定性。首先需要重建状态空间（陈铿 等，2005）。状态空间可以通过延迟坐标嵌入的方式从一维时间序列数据中进行重建：

其中，τ是时间延迟，m是嵌入维度，z（t）是输入的一维坐标系，S（t）是重建的m维状态空间的向量。

时间延迟的选择基于第一平均互信息函数，嵌入维度数量的选择基于伪最邻近算法（Fraser et al.，1986；Kennel et al.，1992）。通过平均交互信息算法计算本研究时间序列数据的时间延迟，平均互信息函数在第一阶段的最小值即为合适的时间延迟；通过伪最邻近算法检查临近轨迹点数量随维度函数的变化情况，伪最邻近数量降低为0 时所对应的维度即为选择的最佳嵌入维度（赵雅琼，2014）。

跑者在（10.8±0.5） km/h 跑步速度下的部分膝关节合角加速度数据如图2 所示。其中，时间延迟为10，嵌入维度为6（图3）。重建后的三维时间延迟数据如图4 所示。

图2 惯性测量单位传感器采集的合角加速度数据Figure 2.Graphical Representation from the IMU Sensor Showing the Resultant Angular Velocity

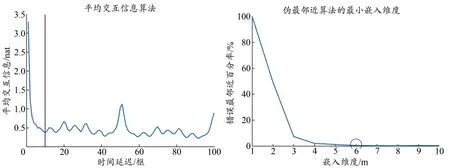
图3 状态空间中时间延迟和嵌入维度的计算Figure 3.Calculations of Time Delay and Embedding Dimension in State Space

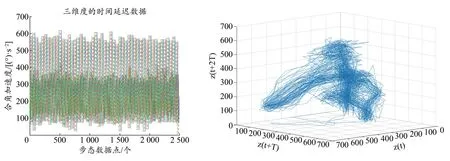
图4 一维和三维空间中的时间延迟数据Figure 4.Time Delay Data in One-Dimension and Three-Dimension Spaces

李雅普诺夫动力学稳定性理论表明了给定系统的动力学对干扰作出的反应。扰动量的大小随时间的变化被评估为距离：

其中，在重建的状态空间中x（0）表示扰动点，xe（0）表示非扰动点。

指数稳定性评估是常用的稳定性构造方法，用于参数化度量扰动量，即d（t）的大小，状态空间中相邻轨迹之间距离的平均增长速率可以表示为：

第j对最邻近点的指数偏移速率与距离的关系可以表达为：

其中，Cj为常数，表示初始分离；e 为自然常数；λ为偏移速率。通过对式（4）取对数得到式（5）：

通过最小二乘法进行一次函数线性拟合，一段时间（t）内的曲线线性拟合斜率可以表达为：

最大Lyapunov 指数λ可以表示为：

1.4 实验方案和过程

根据受试者的鞋码选择3 类对应鞋码的跑鞋。实验开始前，受试者在跑步机（Bertec，Worthington，USA）上穿着传统跑鞋以8 km/h 的速度慢跑5 min。热身结束后，在不影响关节活动的前提下，通过配套绷带将惯性测量单位传感器I Measure U Sensor V1（长×宽×高为40 mm×28 mm×15 mm，质量为12 g，分辨率为16 bit，Vicon Ltd，UK）佩戴于受试者右腿的踝、膝关节贴合皮肤处［2 个传感器分别放置于右腿胫骨近端与远端肌肉和脂肪等软组织较少处（图5）］，以减小传感器在跑步过程中的震动幅度。测试过程中，所有受试者分别穿着3 类跑鞋以（10.8±0.5）km/h 的速度在跑步机上持续跑步12 min。受试者随机选择3 类跑鞋进行测试，完成一类跑鞋的测试后，休息5 min，再穿着下一类跑鞋进行同样的测试。在测试过程中，每位受试者在3 类跑鞋条件下分别记录6 次，持续时长为80 s/次（开始后和结束前的2 min 不计入），每次捕捉约90 个连续步态，选取其中较为稳定的50 个连续步态进行动态稳定性分析（图6）。

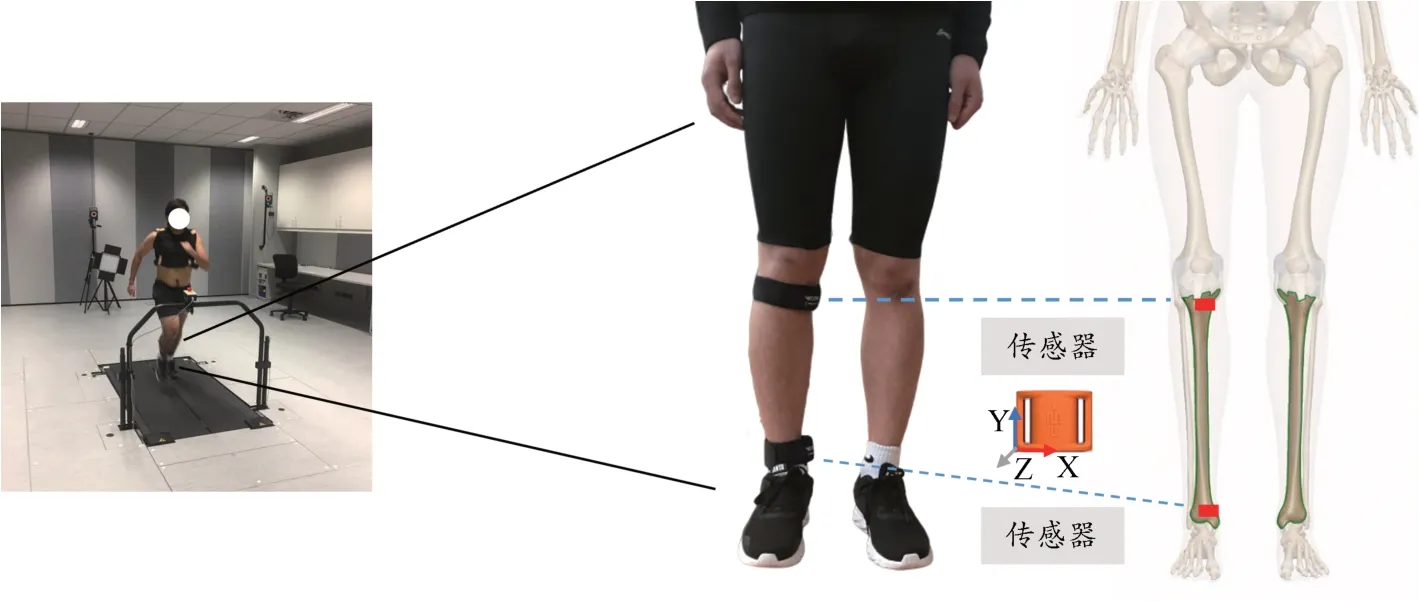
图5 实验过程中传感器的放置位置Figure 5.Placement of Sensors during the Experiment

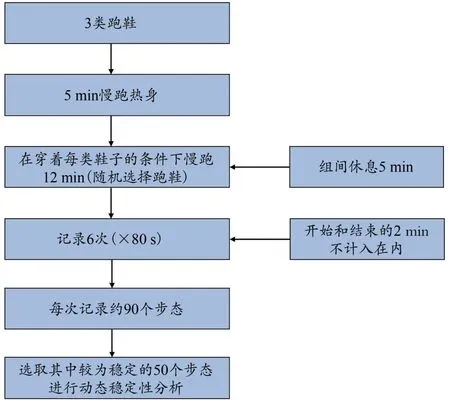
图6 测试过程流程图及数据选取标准Figure 6.Test Flow Chart and Data Selection Criteria

1.5 数据收集与统计分析

通过Vicon Nexus 2.8（Vicon Ltd，UK）同步导出CSV文件格式的加速度原始数据，确定惯性测量单位传感器测得的步态周期，截取连续50 个稳定的步态周期。本研究的实验数据分为踝、膝关节合加速度的峰值以及最大Lyapunov 指数。根据三轴加速度数据通过式（8）计算合加速度，其中加速度数据分为加速度/（m·s-2）和角加速度/［（°）·s-2］数据。

其中，X为内/外方向的加速度数据，Y为垂直方向的加速度数据，Z为前/后方向的加速度数据。

将50 个步态合加速度的时间序列数据分为踝关节和膝关节加速度，每个加速度同样包括加速度和角加速度，计算时间序列数据的嵌入空间和时间延迟，构建状态空间（Dingwell et al.，2000； Terrier et al.，2013）。在Matlab R2018a（Mathworks Inc，Natick，MA）中，通过将计算得出的时间延迟以及嵌入维度赋值到Rosenstein 算法中，计算最大Lyapunov 指数，评估跑步过程中的踝关节和膝关节局部动态稳定性（Rosenstein et al.，1993）。

处理峰值加速度数据的过程如下：1）将获取的原始数据通过截止频率为15 Hz 的二阶低通零滞后Butterworth滤波器进行数据滤波处理；2）将滤波后的数据通过3 次样条插值法（cubic spline interpolation）进行数据标准化处理，获取每个步态约50 个的数据点，即50 个步态共计约2 500 个数据点（Frank et al.，2019）；3）计算数据标准化后的合加速度，统计每个步态的峰值加速度。为了避免改变步态间与步态内数据的时序特性，本研究对计算Lyapunov 指数的数据进行相同的标准化合加速度计算处理，但并未进行滤波处理（Cignetti et al.，2012）。

在GraphPad Prism®8.0.2（San Diego，USA）中采用单因素方差分析进行各组数据的统计学检验，显著性水平设置为P＜0.05。数据分析前通过Shapiro-Wilk 检验进行正态分布检验。通过Brown-Forsythe 检验进行方差齐性检验，若方差齐性不等，则进行Welch ANOVA 检验，组间多重比较采用Tamhane T2 检验；若方差齐性相等，则采用Tukey HSD 检验进行组间比较。对于方差齐性相等的数据组通过Eta 平方（η2）法计算统计分析中数据效应量（effect size，ES）的值。对于采用Welch ANOVA 检验的数据组，通过Omega 平方（ω2）法计算其效应量（Olejnik et al.，2003）。效应量的判断标准：0.01＜ES≤0.06 为小效应量；0.06＜ES≤0.14 为中效应量；ES＞0.14 为大效应量（Cohen，1997）。

2 结果

2.1 峰值加速度

2.1.1 踝关节

跑者在3 类跑鞋条件下50 个步态内踝关节合加速度的峰值具有显著差异（图7），Welch 单因素方差分析显示：F（2，95.54）=545.4，ES=0.96，P＜0.01。Tamhane’s T2 检验的结果显示，相较于传统跑鞋，跑者穿着极致缓震鞋着地时踝关节产生合加速的峰值更小（P＜0.01）；相比于极简跑鞋，跑者穿着极致缓震跑鞋时踝关节合加速度的峰值显著降低（P＜0.01）；相较于传统跑鞋，跑者穿着极简跑鞋时合加速度的峰值显著增加（P＜0.01）。跑者在3 类跑鞋条件下踝关节合角加速度的峰值数据同样具有显著差异（图8），单因素方差分析显示：F（2，147）=476.6，ES=0.87，P＜0.01。Tukey HSD 事后多重检验显示：相较于传统跑鞋，跑者穿着极致缓震鞋产生的峰值合角加速度显著减小（P＜0.01）；相比于极简跑鞋，跑者穿着极致缓震跑鞋着地时的踝关节峰值合角加速度显著减小（P＜0.01）；相比传统跑鞋，跑者穿着极简跑鞋的踝关节合角加速度峰值显著增大（P＜0.01）。

图7 3类跑鞋50个步态内的踝关节峰值合加速度比较Figure 7.Comparison of the Peak Ankle Joint Resultant Acceleration within 50 Gaits in 3 Types of Running Shoes

图8 3类跑鞋50个步态内的踝关节峰值合角加速度比较Figure 8.Comparison of the Peak Ankle Joint Resultant Angular Acceleration of within 50 Gaits in 3 Types of Running Shoes

2.1.2 膝关节

跑者在3类跑鞋条件下50个步态内膝关节合加速度的峰值具有显著差异（图9），单因素方差分析显示：F（2，147）=210.3，ES=0.74，P＜0.01。相较于传统跑鞋，跑者穿着极致缓震跑鞋的膝关节峰值合加速度显著减小（P＜0.01）；相比于极致缓震跑鞋，跑者穿着极简跑鞋时产生的膝关节峰值合加速度更大，且具有显著差异（P＜0.01）；相比于传统跑鞋，跑者穿着极简跑鞋时产生的膝关节峰值合加速度更大（P＜0.01）。跑者在3 类跑鞋条件下50 个步态内膝关节合角加速单因素方差分析显示：F（2，147）=299.0，ES=0.80，P＜0.01，跑者在3 类跑鞋条件下膝关节峰值合角加速度具有显著差异（图10）。相较于传统跑鞋，跑者穿着极致缓震跑鞋产生的膝关节峰值合角加速度更低（P=0.006）；相比于极致缓震跑鞋，跑者穿着极简跑鞋的膝关节峰值合角加速度显著增大（P＜0.01）；相比于传统跑鞋，跑者穿着极简跑鞋时的膝关节峰值合角加速度显著增大（P＜0.01）。

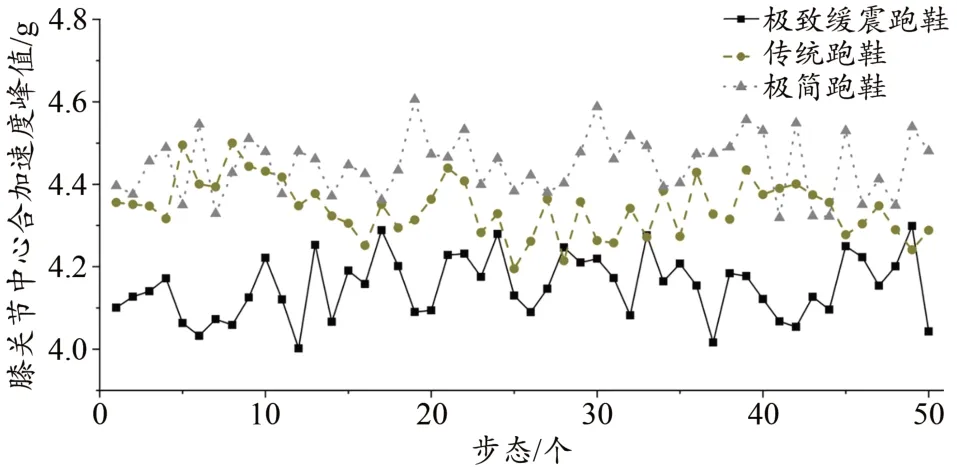
图9 3类跑鞋50个步态内的膝关节峰值合加速度比较Figure 9.Comparison of the Peak Knee Joint Resultant Acceleration within 50 Gaits in 3 Types of Running Shoes

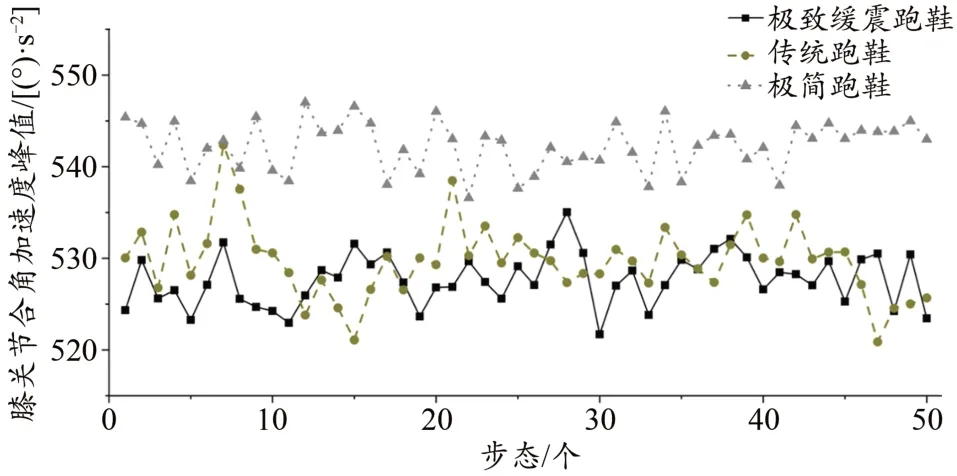
图10 3类跑鞋50个步态内的膝关节峰值合角加速度比较Figure 10.Comparison of the Peak Knee Joint Resultant Angular Acceleration within 50 Gaits in 3 Types of Running Shoes

2.2 最大Lyapunov指数

2.2.1 踝关节

跑者穿着在3 类跑鞋条件下踝关节合加速度的最大Lyapunov 指 数 分 别 为：A 组（0.472±0.15）bits/s，B 组（0.407±0.09）bits/s，C 组（0.339±0.08）bits/s（表1）。3 类跑鞋条件下跑者踝关节合加速度的最大Lyapunov 指数存在显著差异，单因素方差分析显示：F（2，33）=4.52，ES=0.22，具有较高的效应量（P=0.018）。Tukey HSD 检验组间多重比较显示，A 组与B 组间均值差=0.06，95% CI：-0.04，0.17，P=0.317，不具有显著差异；A 组与C 组间均值差=0.13，95% CI：0.02，0.24，P=0.014，具有显著差异。相比于极简跑鞋，跑者穿着极致缓震跑的踝关节合加速度的最大Lyapunov 指数显著增加；相比于极简跑鞋，穿着传统跑鞋踝关节合加速度的最大Lyapunov 指数的平均值增加了0.068 bits/s，95% CI：-0.04，0.18，但差异不显著（P=0.288）。

踝关节合角加速度的最大Lyapunov 指数分别为：A 组（0.74±0.26）bits/s、B 组（0.61±0.17）bits/s、C 组（0.56±0.14）bits/s（表1）。单因素方差分析显示：F（2，33）=2.69，ES=0.14，具有中等的效应量，不具有显著差异（P=0.083）。Tukey HSD 检验显示，A 组与B 组间均值差=0.13，95% CI：-0.07，0.33，P=0.253；A 组与C 组间不具有显著差异（P=0.078），但相比于极简跑鞋，跑者穿着极致缓震跑鞋的踝关节合角加速度最大Lyapunov指数的平均值增加了0.18 bits/s，95% CI：-0.02，0.38；相比于极简跑鞋，穿着传统跑鞋的平均值增加了0.05 bits/s，95% CI：-0.15，0.25，但差异不具有统计学意义（P=0.805）。

表1 踝关节合加速度和合角加速度的最大Lyapunov指数的单因素方差分析结果Table 1 One-Way ANOVA Analysis Results of Largest Lyapunov Exponents of Ankle Joint Resultant Acceleration and Angular Acceleration

2.2.2 膝关节

3 类跑鞋条件下膝关节合加速度的最大Lyapunov 指数分别为：A 组（0.936±0.12）bits/s、B 组（0.937±0.15）bits/s、C 组（0.652±0.20）bits/s（表2）。跑者在3 类跑鞋条件下膝关节中心合加速度的最大Lyapunov 指数数值具有显著差异（P＜0.01）。单因素方差分析显示，具有较高的效应量［F（2，33）=12.76，ES=0.44］。Tukey HSD 检验显示，A 组与B组的均值差为-0.000 2，95% CI：-0.16，0.16，P=0.999 6；A组与C 组间均值差=0.28，95% CI：0.12，0.44，P=0.000 3，具有显著差异。相比于极简跑鞋，跑者穿着极致缓震跑鞋时的膝关节合加速度最大Lyapunov 指数显著增大；B 组与C 组间差异显著（P=0.000 3），相较于极简跑鞋，跑者穿着传统跑鞋的最大Lyapunov 指数显著增大，平均值增加0.285 bits/s，95% CI：0.13，0.45。

3 类跑鞋条件下膝关节合角加速度的最大Lyapunov 指数分别为：A 组（0.456±0.15）bits/s、B 组（0.414±0.13）bits/s、C 组（0.380±0.10）bits/s（表2）。单因素方差分析显示，效应量较小［F（2，33）=1.02，ES=0.06］，跑者在3 类跑鞋条件下膝关节合角加速度的最大Lyapunov 指数不存在显著差异（P=0.373）。Tukey HSD 检验显示，A 组与B 组间均值差=0.04，95% CI：0.09，0.17，P=0.72；A 组与C 组间不具有显著差异（P=0.341），但相比极简跑鞋，跑者穿着极致缓震跑鞋膝关节合角加速度的最大Lyapunov 指数平均值增加了0.076 bits/s，95% CI：-0.05，0.20；B 组与C 组间无显著差异［均值差=0.03，95% CI：-0.10，0.16，P=0.795）］。

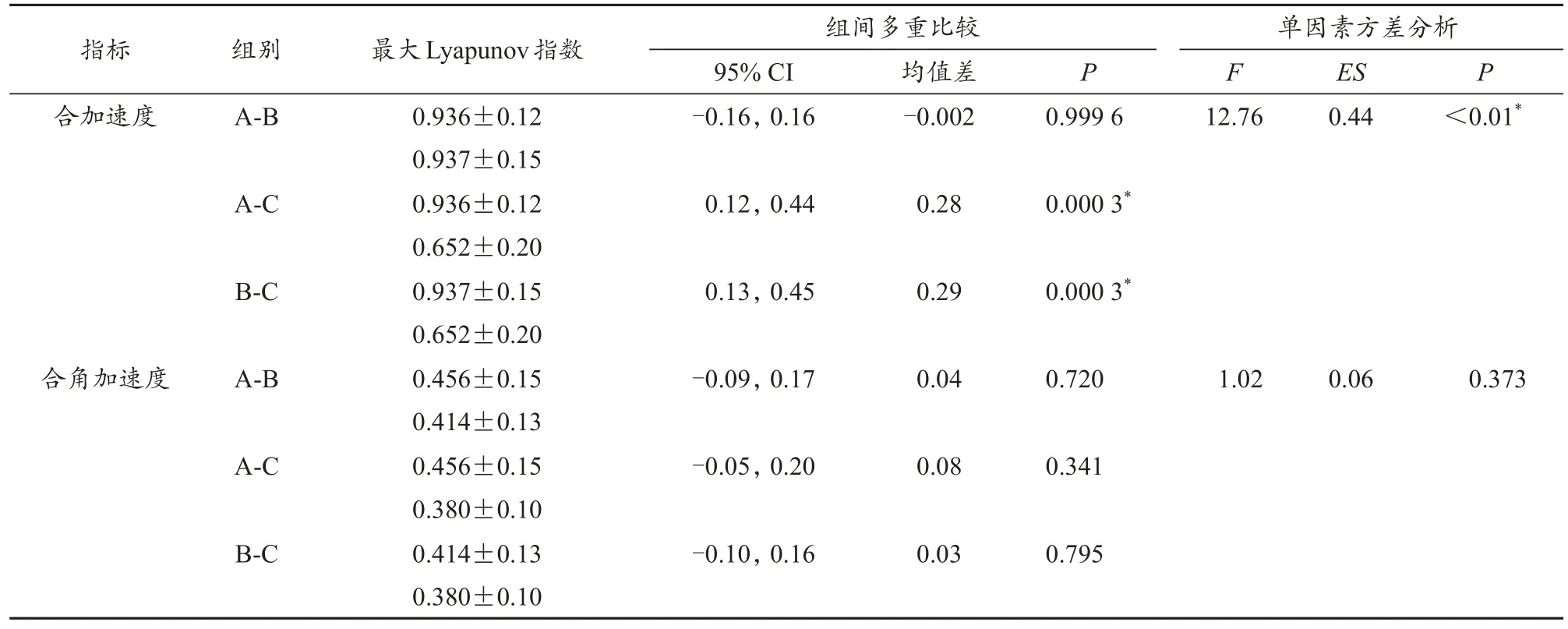
表2 膝关节合加速度和合角加速度的最大Lyapunov指数的单因素方差分析结果Table 2 One-Way ANOVA Analysis Results of Largest Lyapunov Exponents of Knee Joint Resultant Acceleration and Angular Acceleration

3 分析与讨论

本研究通过Rosenstein 算法（Rosenstein et al.，1993），计算跑者穿着传统跑鞋、极致缓震跑鞋和极简跑鞋跑步的过程中所产生时间序列数据的最大Lyapunov 指数。采用惯性测量单位传感器收集跑者膝、踝关节恒定速度下50 个连续且稳定步态的加速度数据，进行峰值合加速度比较，然后计算时间序列数据的时间延迟和嵌入维度，构建状态空间，计算最大Lyapunov 指数。本研究发现：对于峰值合加速度，无论是膝关节还是踝关节，极简跑鞋最大，而极致缓震跑鞋最小，且均具有显著差异；对于最大Lyapunov 指数，跑者穿着极致缓震跑鞋和极简跑鞋的踝关节合加速度差异显著，相较于极致缓震跑鞋，跑者穿着极简跑鞋的最大Lyapunov 指数更小，即动态稳定性更好。跑者穿着极致缓震跑鞋与传统跑鞋以及极致缓震跑鞋与极简跑鞋组间的膝关节合加速度差异显著，相较极致缓震跑鞋，传统跑鞋和极简跑鞋的最大Lyapunov 指数更小，即动态稳定性更好。

3.1 胫骨峰值加速度

踝关节合加速度峰值又称胫骨峰值加速度（peak tibia acceleration，PTA-R）。研究发现，更大的PTA-R 与更高的损伤率有关（Sheerin et al.，2020）。后跟着地模式的跑者着地时产生的胫骨应力大于前足着地模式的跑者（Ruder et al.，2019）。Sinclair（2017）研究发现，相较于极简跑鞋，跑者穿着极致缓震跑鞋着地时所产生的PTA-R 显著增大。但相关研究发现，相较于传统跑鞋和极致缓震跑鞋，穿着极简跑鞋的跑者所产生的瞬时垂直负荷加载率更大（Agresta et al.，2018；Sinclair et al.，2016）。Becker 等（2020）研究发现，极致缓震跑鞋跑步过程中臀大肌和腓骨长肌的均方根振幅小于传统跑鞋和极简跑鞋。Willy 等（2014）针对传统跑鞋和极简跑鞋的动力学研究发现，相较于传统跑鞋，跑者适应初期穿着极简跑鞋落地时产生的峰值垂直冲击载荷以及平均垂直负荷加载率均显著增大。

本研究发现，跑者穿着极简跑鞋产生的PTA-R 大于传统跑鞋，穿着传统跑鞋的胫PTA-R 大于极致缓震跑鞋。提示，跑者所产生的PTA-R 差异可能与跑鞋的类型相关，其中极致减震跑鞋产生的PTA-R 最小，而极简跑鞋产生的PTA-R 最大。因此，跑者不仅应注意在穿着极简跑鞋进行跑步的初期阶段由于不适应所造成的损伤，还需要注意极简跑鞋可能增加跑步过程的瞬时垂直加载速率和PTA-R，进而造成慢性损伤这一问题（Sinclair et al.，2016）。

极致缓震跑鞋前足和中足区域的中底厚，掌跟差较小，设计重点在突出跑鞋的缓冲减震作用，以降低冲击载荷，减少足-地接触所产生的相关损伤（Pollard et al.，2018）。Agresta 等（2018）通过对习惯穿着传统跑鞋跑步的人群进行为期4 周的极致缓震跑鞋和极简跑鞋跑步训练发现，相较于传统跑鞋，穿着极致缓震跑鞋和极简跑鞋的跑者着地时产生的冲击载荷增大，但极简鞋所产生的PTA-R 和足跟峰值加速度更大。极简跑鞋还会产生相较传统跑鞋和极致缓震跑鞋更大的瞬时负荷加载率（Hannigan et al.，2020）。相关的肌电研究表明，穿着极致缓震跑鞋跑者产生的胫骨前肌均方根幅值低于极简跑鞋（Becker et al.，2020）。因此，跑者在由穿着传统跑鞋改为极致缓震跑鞋的适应初期，其损伤概率可能小于由穿着传统跑鞋改为极简跑鞋的适应初期。这与本研究发现的3 类跑鞋跑者下肢关节峰值合加速和合角加速度的结果一致，也说明了即使长期穿着极简跑鞋跑步具有增强足部内、外部肌肉力量，提高足纵弓刚度等长期效应，但短期内也会增加下肢骨骼、肌肉损伤风险，因此从短期角度而言，人体更易于适应穿着极致缓震跑鞋进行跑步运动。

3.2 下肢局部动态稳定性

局部动态稳定性是测量人体动态平衡的重要指标之一，可以通过计算人体生物力学时间序列数据的最大Lyapunov 指数进行评估（李立 等，2014；吕金虎 等，2002；Look et al.，2013）。惯性加速度传感器获得的三轴加速度时序数据可以评估不同速度下步态局部动态稳定性差异。Stenum 等（2014）研究发现，不同最大Lyapunov 指数计算方法和不同步态速度均会造成局部动态稳定性的差异。一定条件下，步行速度越小，动态稳定性表现越好，同时局部动态稳定性还受不同跑步界面的影响（England et al.，2007）。Ekizos 等（2017）测试习惯穿着传统跑鞋跑步的跑者在跑步机上裸足和穿着传统跑鞋条件下跑步时的局部动态稳定性发现，急性裸足跑步态的动态稳定性更差，损伤风险更高，但是尚不清楚这种差异的原因是由于不同着鞋条件还是着地模式的改变造成的。

Frank 等（2019）比较初级跑者和具有长期跑步经验的跑者在穿着不同厚度（传统跑鞋 vs 极简跑鞋）和鞋底硬度跑鞋的条件下髋、膝和踝3 个关节局部动态稳定性发现，除了跑步经验对最大Lyapunov 指数产生显著影响外，不同鞋底厚度和硬度间不存在显著差异。该研究还发现，髋关节在上述不同条件下最大Lyapunov 指数的变化小且较稳定，而末肢关节踝关节的最大Lyapunov 指数受外界条件的影响最大。本研究发现针对踝关节和膝关节合加速度的最大Lyapunov 指数，传统跑鞋小于极致缓震跑鞋但大于极简跑鞋，并且跑者穿着极致缓震跑鞋时膝关节和踝关节合加速度的最大Lyapunov 指数显著大于极简跑鞋，跑者穿着极简跑鞋时膝关节合加速度的最大Lyapunov 指数显著小于传统跑鞋。从局部动态稳定性的角度，说明穿着极简跑鞋的下肢局部动态稳定性最佳，而极致缓震跑鞋的局部动态稳定最差。

结合Lieberman 等（2010）、Davis 等（2017）和Sinclair（2017）针对不同着地模式、着鞋条件和鞋底厚度等方面对人体足内外部神经肌肉活动、足纵弓功能以及运动损伤影响的研究认为，极简跑鞋更适合于跑者。结合3 类跑鞋的下肢关节峰值合加速度表明，虽然极致缓震跑鞋的局部动态稳定性较差，但是由于其下肢关节峰值合加速度小，前足和后足厚大的中底能够在跑步过程中一定程度上起到缓冲减震、减小由于着地冲击载荷和PTA-R 过大等因素导致的相关运动损伤的作用（Agresta et al.，2018；Sinclair et al.，2016）。

4 结论

1）从下肢关节峰值加速度的角度考虑，极致缓震跑鞋较传统跑鞋和极简跑鞋具有更好的缓冲减震作用，着地时的胫骨峰值加速度更小。

2）从局部动态稳定性的角度考虑，极简跑鞋较极致缓震跑鞋和传统跑鞋在跑步的过程中具有更好的下肢局部动态稳定性，系统减弱外部干扰的能力更好，说明跑者着极简跑鞋跑步时的步态更自然。

3）传统跑鞋组由于产生的下肢关节峰值加速度相对较小且具有较好的局部动态稳定性，对于需要兼顾跑步时的缓冲减震作用以及动态稳定性的跑者来说是较优的选择。