基于半隐式运动粒子法的减速器搅油损失计算及试验验证

徐占 张冰 王溪 赵雪松 白学斌

（1.中国第一汽车股份有限公司研发总院，长春 130013；2.苏州舜云工程软件有限公司，苏州 215100）

主题词：减速器 搅油损失 半隐式运动粒子法 传动效率

1 前言

电动汽车减速器内部的功率损失主要包括齿轮啮合损失、轴承摩擦损失和系统搅油损失。其中，搅油损失占比较大，尤其是在高速和高油位的情况下[1]。因此，深入研究减速器搅油损失对减速器效率的提升具有重要意义。

由于搅油损失对减速器效率影响较大，近年来，众多学者投入到搅油损失的研究中。Ji等[2]运用无网格光滑粒子法（Smoothed Particle Hydrodynamics，SPH）在不同雷诺数和油位条件下进行了多组数值仿真，并试验验证了仿真结果。Chen和Matsumoto[3]对8 种异构齿轮减速器进行了搅油试验，并应用半隐式运动粒子法（Moving Particle Semi-implicit method，MPS）进行了相应仿真分析，从润滑油速度、流态、搅油损失3个方面分析仿真计算结果，探索箱体结构对搅油损失的影响。李晏等[4]应用MPS研究了单个齿轮的不同转速、浸油深度和齿宽等条件对搅油损失的影响，并依据仿真结果搭建了单个斜齿轮搅油损失数学模型。Liu 等[5]基于有限体积法搭建了FZG单级齿轮箱搅油损失仿真模型，研究了FZG 单级齿轮箱内的润滑油分布和搅油损失。周雅杰等[6]搭建了齿轮箱内部流体空间的有限元模型，采用求解压力耦合方程组的半隐式方法（Semi-Implicit Methods for Pressure Linked Equations，SIMPLE）与流体体积函数（Volume of Fluid，VOF）两相流理论并应用该模型分析啮合区油液、齿轮圆周面的流体分布，以此进行齿轮搅油损失的计算。Changenet 等[7]搭建了一个壁面可移动的试验台架，研究了径向间隙和轴向间隙对齿轮副搅油损失的影响规律。Concli 等[8-9]应用数值仿真方法进行了不同转速、浸油深度和温度条件对齿轮副搅油损失与齿轮啮合区的挤压损失影响的研究，并应用试验验证了仿真结果。

上述关于搅油损失的研究中，多数是针对单对或单个齿轮的简单系统的研究，针对多对齿轮复杂系统的研究较少，且未在10 000 r/min 转速以上的高速工况下开展验证。本文针对多对齿轮啮合的复杂系统和湍流作用强烈的高速工况，提出结合Smagorinsky 湍流模型和多面体壁面模型提升减速器搅油损失计算精度的方法，并通过试验验证该方法的有效性，最后分析某减速器循环工况中搅油损失的占比。

2 搅油损失计算

2.1 半隐式运动粒子法

2.1.1 基本控制方程

计算流体力学（Computational Fluid Dynamics，CFD）分为欧拉体系和拉格朗日体系，传统的半隐式运动粒子法是一种基于拉格朗日体系的CFD方法。粒子法的主要控制方程包括：

连续性方程：

动量方程：

能量方程：

式中，ρ为液体密度；t为时间；u为粒子速度；p为流体压强；ν为运动粘性系数；f为体积力；H为焓；k为导热系数；T为流体温度；Q为体积内热源。

2.1.2 方程的求解

动量方程的求解采用半隐式方法，能量方程的求解采用显式方法，扩散项和体积源项乘以时间步长就可以直接得到每个时间步长后焓的变化，然后再用新的焓值计算流体温度。

基于不可压缩流体的质量守恒定律，压力泊松方程由流体的连续性方程推导而来。将式（2）的时间项离散后，可以得到：

该方程经过移项可以变形为：

式中，un为当前时间步速度；un+1为下一时间步速度。

预测速度为：

式中，u*为速度预测值。

由式（5）、式（6）可得：

将式（7）两边同时取散度可得：

根据不可压缩流体的连续性方程，式（8）的左侧恒等于0，右侧可以变形为：

由式（1）可得质量守恒方程为：

将式（9）代入式（10），可以得到压力泊松方程为：

根据Koshizuka[10]提出的模型，式（11）右侧源项的计算求解为：

式中，ρ*为密度中间状态；n*为当前粒子的粒子数密度；n0为初始粒子数密度。

H.Gotoh[11]提出了高阶源项模型，该模型在三维条件下可以写成：

式中，re为影响半径；ri、rj分别为编号为i、j的流体粒子的位置坐标；分别为编号为i、j的流体粒子的预测速度。

方程左侧拉普拉斯运算可展开为：

如果采用高阶源项模型，可得到线性方程组如下：

式中，d为维数；pi、pj分别为编号为i、j的流体粒子的压力；λ为预计算常数；ω为权重函数。

本文将Koshiuka 提出的经典源项模型和H.Gotoh提出的高阶源项模型有机结合[12]，分别乘以权重因子α和(1-α)，然后加和：

根据工程实践经验，取α=0.05可以达到较高的数值稳定性。

搅油力矩的计算公式为：

式中，M为搅油力矩；r为刚体表面某一点到转轴的矢量距离；n为表面法向量；ps为表面的压力；τt为壁面湍流切应力；s为表面积。

2.2 高精度搅油损失计算模块

搅油力矩主要来源于壁面的压力和壁面湍流切应力，其中刚体受到的压力差可以通过粒子的压力场计算。本文采用的湍流模型和多面体壁面模型对搅油过程中壁面受到的湍流切应力的计算精度提升起到了关键作用。Smagorinsky 湍流模型可以修正来自小于粒子尺寸的湍流粘性力导致的壁面切应力的误差，提高切应力计算精度。多面体壁面边界可以更加精细地保留齿轮齿形等几何特征，相比传统粒子壁面几何还原度更高。

2.2.1 湍流模型

亚格子湍流模型（SubGrid-Scale，SGS）最早用于大涡模拟，是一种基于网格法的模型。类似地，在MPS中，亚粒子湍流模型（Subparticle-Scale）被提出，并在Arai[13]、Duan和Chen[14]以及Li[15]的研究中使用。速度矢量ui可以分解为空间平均量和波动量，代入式（2）可得：

式中，δij为德塔函数。

为了改进湍流作用强烈情况下的模拟计算，研究使用零方程湍流模型[16]。在该模型中，由于湍流引起的动量和能量扩散效应体现在湍流运动粘度νt和湍流导热系数kt上，故νt的表达式为：

式中，Cs为Smagorinsky常数；ΔX为粒子间距。

2.2.2 多体壁面模型

本文所使用的多面体壁面（Polygon Wall）模型区别于传统粒子法所使用的粒子壁面（Particle Wall）模型。传统的粒子壁面虽然在数值处理方面相对简便，但是对于复杂几何形状的还原度差，不能够体现减速器壳体加强筋和导油筋等复杂几何体细节结构对流场的影响，且近壁面压力场和速度场受粒子排布形状影响较大。传统的显式多面体壁面边界方法[17]仅考虑壁面的压力和方向，缺少壁面粒子分布信息。Matsunaga等[18]提出的积分多面体边界方法由于计算量非常大，不适合工程实际问题求解。为了实现更精确高效的多面体几何壁面边界条件，本文提出“移动虚拟邻居粒子（Travelling Potential Ghost Neighbour Particles）”的概念。这种移动虚拟邻居粒子跟随每一个流体粒子i移动，其与每个流体粒子的相对位置固定不变。移动虚拟粒子就像一个围绕在粒子i周围的球型的粒子云，其半径为粒子的影响半径。

在流体流动中，一旦粒子i靠近一个多面体几何壁面，部分虚拟邻居粒子会穿过多面体进入几何实体内部。进入多面体几何实体内部的移动虚拟邻居粒子会被假想为真实的壁面粒子边界，称为虚拟壁面粒子（Ghost Wall Neighbour Particles）。这些虚拟壁面粒子在数值求解中并不真实存在，因此也并不会进入压力场求解。

进入多面体几何实体的移动虚拟邻居粒子会发挥壁面边界粒子的作用，阻碍流体粒子穿过多面体壁面边界，如图1 所示。这些虚拟壁面粒子会加入泊松方程源项的计算，假设虚拟壁面粒子的压力等于流体粒子i上一时间步的压力，在压力梯度的计算中，也会假设虚拟壁面粒子的压力等于流体粒子i的压力。在动量方程中，虚拟壁面粒子的速度等于多面体几何壁面的速度[12]。

图1 移动背景邻居粒子和多面体边界

在引入虚拟壁面粒子用于模拟多面体壁面边界条件后，泊松压力方程变形为：

主对角线元素扩展为：

非主对角线元素仍然保持不变:

包含多面体壁面边界的源项为：

式中，pvir为虚拟粒子的压力；ni,vir为虚拟粒子i的粒子数密度；Sgho为镜像粒子合集；pgho为镜像粒子的压力；ngho为镜像粒子的粒子数密度。

其中，虚拟壁面粒子权重的总和为：

在泊松方程的求解中，假设虚拟壁面粒子的压力等于粒子i上一时间步的压力：

3 仿真计算结果

3.1 计算流程

以上所提到的所有计算模型均在半隐式粒子法软件shonDy中集成。在设定好几何输入、物性参数、求解器以及完成划分计算区域等前处理步骤后，运动粒子法的主要计算流程如图2所示。

图2 粒子法计算流程

3.2 搅油损失计算

应用shonDy软件进行某三平行轴减速器搅油损失仿真计算，减速器3D模型如图3所示。

图3 三平行轴减速器3D模型

将减速器3D 模型分为壳体、输入轴、中间轴和输出轴4 个部分并分别导出.stl 文件，在shonDy 软件中导入上述.stl 文件，设置输入轴转速为1 500 r/min、2 500 r/min、3 500 r/min、4 500 r/min、5 500 r/min、6 500 r/min、7 500 r/min、9 000 r/min、12 000 r/min，中间轴和输出轴转速按速比2.81和8.79计算，输入润滑油材料属性，如表1所示。

表1 润滑油材料属性

取粒子直径为1 mm，加油量为1.62 L，设置重力方向、计算时长等参数后进行仿真计算，搅油损失计算结果如图4所示。

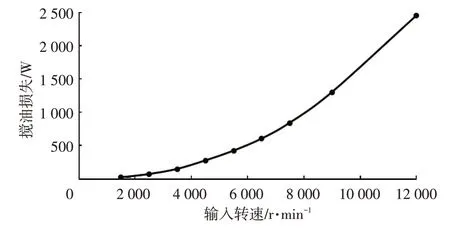
图4 搅油损失计算结果

将湍流模型和多体壁面模型嵌入shonDy软件算法中，按与表1同样的输入条件重新进行减速器搅油损失仿真计算，搅油损失修正计算结果如图5所示。

4 试验验证

4.1 搅油损失试验

4.1.1 试验台架

减速器搅油损失试验台架包括输入电机、输入扭矩传感器、减速器和相关连接夹具，如图6 所示。输入电机采用高速电机，最高转速为15 000 r/min；输入扭矩传感器量程为50 N·m，扭矩不确定度为0.1%～0.2%F·S，重复性≤0.1%F·S，过载能力为150%F·S。

图6 减速器搅油损失试验台架

4.1.2 试验方法

首先在减速器中添加规定量的润滑油，运转输入电机，当减速器油温满足45±5 ℃条件时，测试不同转速下的空载拖曳扭矩；然后将润滑油全部放出，测试不同转速下的空载摩擦扭矩。搅油扭矩为空载拖曳扭矩与空载摩擦扭矩的差。

4.1.3 试验结果

应用上述试验台架和方法进行减速器搅油损失试验，试验工况如表2所示，试验结果如图7所示。

表2 减速器搅油损失试验工况

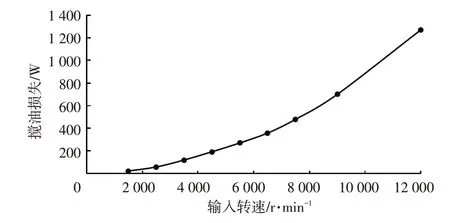
图7 减速器搅油损失试验结果

4.2 搅油损失精度验证

将搅油损失仿真结果与试验结果进行对比，搅油损失仿真平均精度约为47%，对比结果如图8所示。将搅油损失修正结果与试验结果进行对比，搅油损失修正仿真平均精度约为91%，对比结果如图9所示。试验结果表明，经过湍流模型与多体壁面模型的修正，减速器搅油损失仿真精度有较大提升。

图8 搅油损失仿真与试验结果对比

图9 搅油损失仿真修正与试验结果对比

4.3 搅油损失对循环工况效率的影响

在中国轻型汽车行驶工况（China Light-duty vehicle Test Cycle，CLTC）循环中，齿轮啮合损失、轴承摩擦损失和系统搅油损失占比分别为38%、8%和54%。将搅油损失减半和全部去除后，理论上CLTC循环效率从96.96%分别提升至97.87%和98.78%，结果显示，降低搅油损失能够有效提升减速器循环工况效率。

5 结束语

为提升搅油损失的计算精度，本文基于半隐式运动粒子法，通过湍流模型和多体壁面模型修正了搅油损失的算法，并分析了不同搅油损失对CLTC 循环的影响，可以得到以下结论：

a.高速工况下，传统方法在复杂系统和湍流作用强烈的工况中计算精度较差，高速工况下尤为明显，采用改进的搅油损失计算方法可以有效提高计算精度，经试验验证，该方法可以将搅油损失计算精度提升至91%。

b.CLTC循环中，搅油损失对传动效率影响显著，通过降低加油量、旋转体加包裹和主动润滑等手段可以有效降低搅油损失，提升CLTC循环下减速器的效率。