基于深度强化学习的THS-Ⅲ平台PHEV能量管理策略研究*

张小俊 沈亮屹 唐鹏 史延雷 李彦辰

（1.河北工业大学，天津 300401；2.中国汽车技术研究中心有限公司，天津 300300）

主题词：深度强化学习 插电式混合动力汽车 能量管理 层归一化 自适应巡航

1 前言

混合动力汽车同时配备电动机和内燃机，在减少能源消耗的同时可保证较长的续航里程，但多动力源提高了驱动系统的结构复杂度，故对混合动力汽车的能量管理策略进行研究具有重要意义。

目前，基于规则的能量管理策略因设计简单、易于实现[1-2]而被广泛应用。基于规则的能量管理策略依赖于一组简单的规则，不需要驾驶条件的先验知识，且具有很高的鲁棒性，但是缺乏灵活性和适应性[3]，因而基于优化的能量管理策略被提出，动态规划算法[4]、模型预测控制[5]与等效燃油消耗最小策略[6]是较为常见的方法[7]。但是动态规划算法很难应用于实时问题[8]，而模型预测控制与等效燃油消耗最小策略无法对车速进行精准预测。

随着人工智能技术的发展，基于深度强化学习（Deep Reinforcement Learning，DRL）的能量管理策略近年受到广泛关注。Qi 等人使用深度Q 学习（Deep QLearning，DQL）算法对某混合动力汽车的驾驶数据进行处理，提出了最佳燃料使用策略[9]。Han 等人使用更为精准的双Q 学习（Double Deep Q-Learning，DDQL）算法解决了DQL 算法的过估计问题，使得车辆燃油经济性提高了7.1%[10]。

DQL算法更适用于离散型动作，在连续动作的应用上稍显欠缺。王勇等人对THS 平台的混合动力汽车建立了后向仿真模型，将更加适用于连续动作的深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法应用在此模型中，发现使用DDPG 算法的车辆燃油经济性较基于规则的能量管理策略提升了19%[7]。Fujimoto 等人在DDPG 基础上进行改进，得到了双延迟深度确定性策略梯度（Twin Delayed Deep Deterministic policy gradient，TD3）算法[11]。

目前，基于深度强化学习的混合动力汽车能量管理研究已经取得了一定的成果，但大多建立在后向仿真模型基础上，很难模拟真实的驾驶过程。因此，本文对THS-Ⅲ平台的插电式混合动力汽车建立前向仿真模型，建立其能量管理的马尔可夫过程，应用DDPG 和TD3算法进行能量管理策略研究，并将该策略应用于自适应巡航工况中，对基于深度强化学习的能量管理策略进行验证。

2 THS-Ⅲ平台的PHEV模型建立

功率分流式插电式混合动力汽车（Plug-in Hybrid Electric Vehicle，PHEV）的结构和控制最为复杂，THS-Ⅲ平台的PHEV 是功率分流型PHEV 的代表[12]。因此本文对THS-Ⅲ平台的PHEV进行闭环前向仿真模型的搭建，以便还原真实的驾驶过程，优化能量管理策略。

2.1 整车模型的建立

前向仿真模型常用于汽车的完整设计过程，它可以较大程度地还原车辆的真实运行状态，提高仿真的真实性和可靠性[13]，故本文选择建立THS-Ⅲ平台PHEV的前向仿真模型，其结构如图1所示。

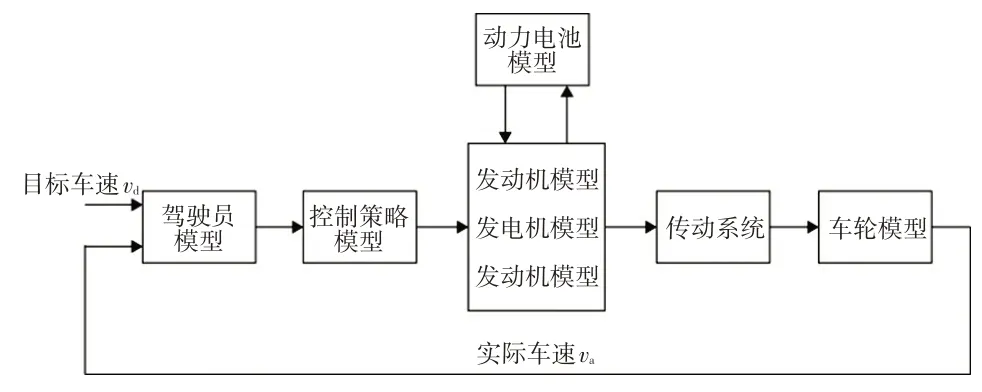
图1 车辆前向仿真模型结构示意

THS-Ⅲ平台插电式混合动力汽车结构如图2 所示，它主要由发动机、电动机、发电机、电池和功率分流机构组成。发动机、电动机和发电机通过2个行星齿轮和动力耦合装置将动力传输至差速器，通过车桥驱动汽车。

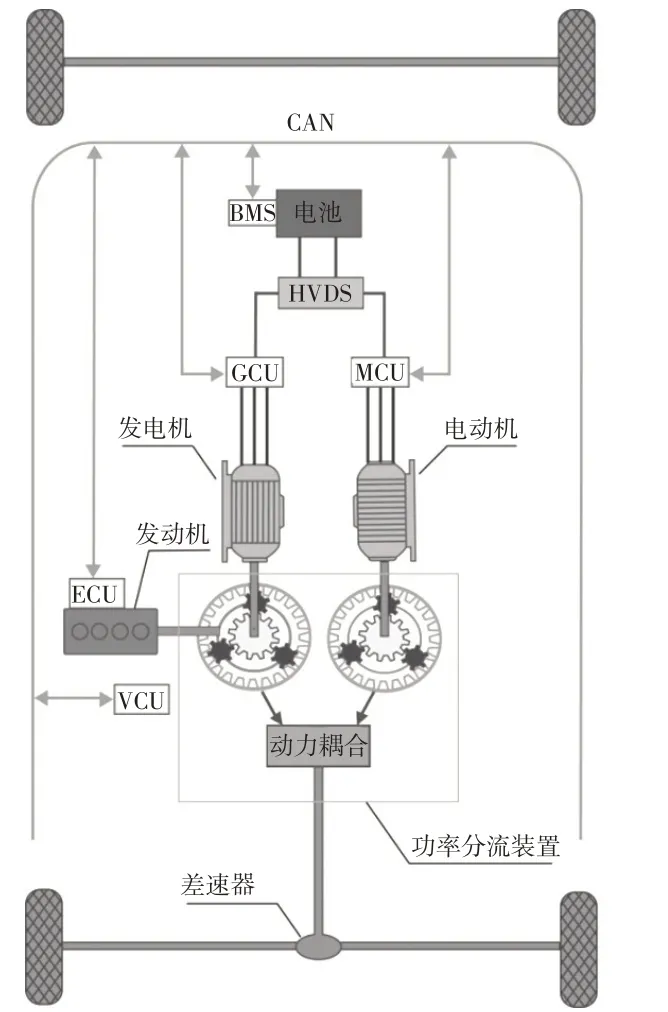
图2 THS-Ⅲ平台插电式混合动力汽车结构

2.2 车辆主要参数和约束条件

发动机万有特性曲线如图3所示，本文的发动机工作点均在图中最佳燃油消耗率曲线上。

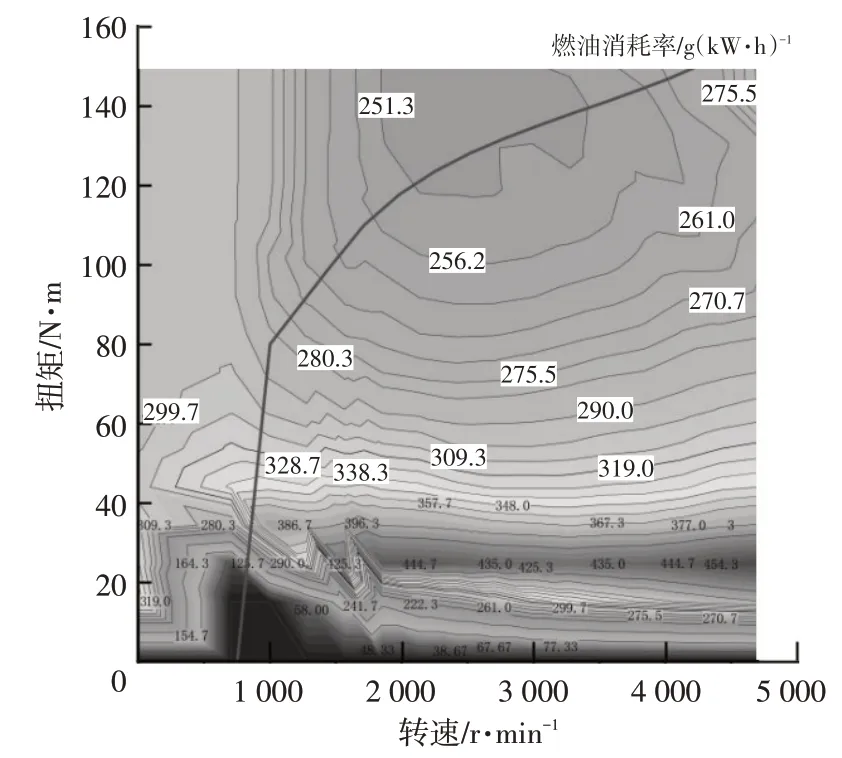
图3 发动机万有特性

通过图3可以得到燃油消耗率mf，通过查表可以得到发电机效率ηm和电动机效率ηg：

式中，ωeng、Teng分别为发动机转速和转矩；σeng为发动机查表函数；ωm、Tm分别为电动机转速和转矩；σm为电动机查表函数；ωg、Tg分别为发电机转速和转矩；σg为发电机查表函数。

闭环前向仿真模型通过驾驶员模型来模拟真实的油门踏板和制动踏板开度。通过油门踏板开度可以得到车辆所需的总功率Pr，功率流平衡方程满足：

式中，Peng、Pele分别为发动机和电动机的功率。

出于安全考虑，车辆电池的荷电状态（State of Charge，SOC）应限制在[0.3,0.8]范围内。车辆的ωeng、ωm、ωg、Teng、Tm、Tg等参数均应满足自身的约束条件，车辆主要参数如表1所示。

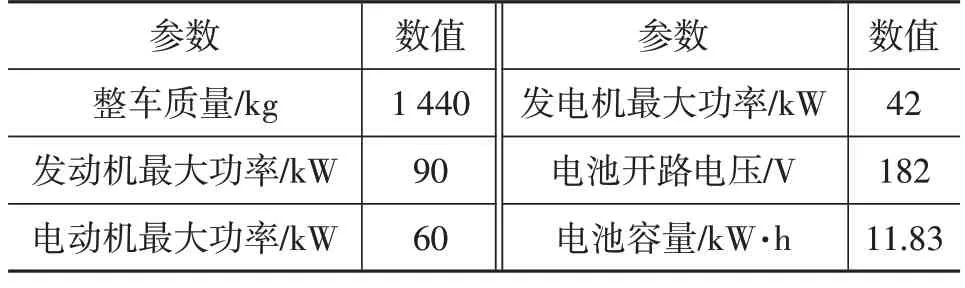
表1 车辆主要参数

3 深度强化学习

深度强化学习（DRL）的出现为人工智能的实现提供了理论基础。一方面，深度学习对策略和状态具有强大的表征能力，能够用于模拟复杂的决策过程；另一方面，强化学习（Reinforcement Learning，RL）赋予智能体自监督学习能力，使其能够自主地与环境交互，在试错中不断进步[14]。

3.1 马尔可夫决策过程

马尔可夫决策过程（Markov Decision Process，MDP）是深度强化学习的理论基础，适用于解决序列决策问题。用元组(S,A,P,R,γ)来描述马尔可夫决策过程，其中S为有限的状态集合，A为有限的动作集合，P为状态转移概率，R为奖励函数，γ为折扣因子。马尔可夫性是指系统的下一个状态只与当前状态有关，而与历史状态无关，其数学描述可表示为：

在式（5）的状态转移过程中会产生奖励函数R，在给定一个策略π的前提下，智能体累积获得的奖励Gt为：

式中，γk为折扣因子；Rt+1+k为(t+1)时刻的即时奖励函数。

本文希望智能体能够与其所处的环境进行交互，根据环境反馈来学习最佳行为，并通过反复试验不断改进行动策略，选择累计回报值最大的策略：

式中，π(s,a)为策略函数；E为均值函数。

为了获得最优策略，需要对每个动作的价值进行评估：

式中，Rt+1为(t+1)时刻的即时奖励；Q(St+1,At+1)为(t+1)时刻的Q值；Eπ为采取π策略下的均值函数；Qπ(s,a)为采取策略π时，在s状态下采取动作a的价值。

在深度强化学习中，可以利用神经网络的强大表征能力来代替传统强化学习中的Q表，通过更新神经网络中的参数θ表示某一动作的Q值，得到每个状态的最佳Q值：

式中，Q*(s,a)为s状态下的最佳Q值。

通过最大化Q值，产生最佳策略π*(s,a)：

式中，π*(s,a)为在s状态下的最佳策略。

3.2 层归一化与深度强化学习

在监督学习中，数据归一化可以缩短训练时间、提升网络稳定性[15]。在深度强化学习中，层归一化（Layer Normalization，LN）已应用于分布式深度确定性梯度策略（Distributed Distributional DDPG，D4PG）和近端策略优化（Proximal Policy Optimization，PPO）算法[16-17]。Bhatt等人将层归一化与DDPG算法进行融合，在某些环境下的训练中获得了良好效果[18]。

层归一化针对单个训练样本进行，不依赖于其他数据，将输入的元素xi归一化为

将归一化层加入到演员（Actor）网络和评论家（Critic）网络的输入层，如图4所示。

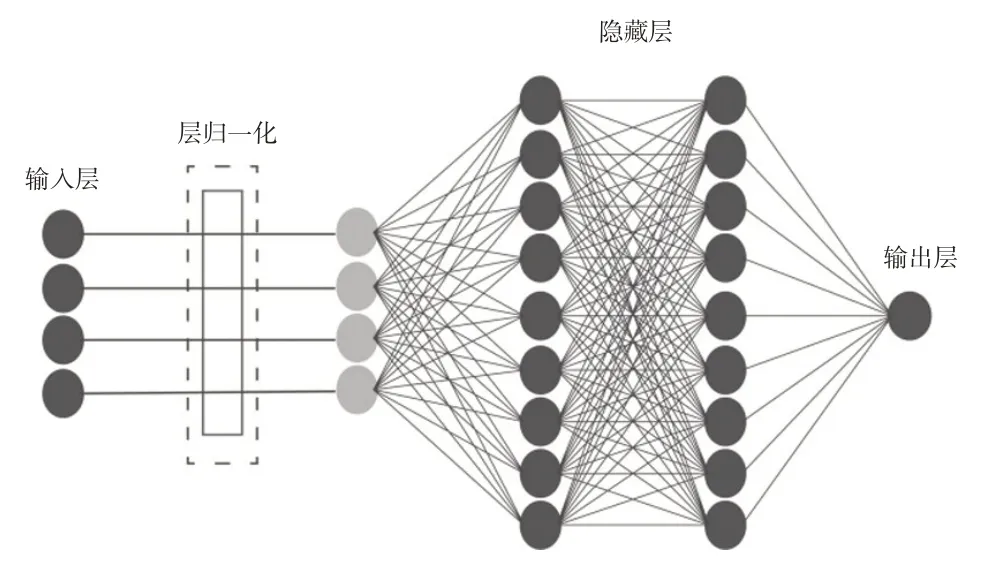
图4 神经网络结构示意

3.3 DDPG与TD3算法

DeepMind 团队基于演员-评论家（Actor-Critic）算法框架，结合确定策略梯度（Deterministic Policy Gradient，DPG）开发出DDPG 算法。基于确定策略梯度的深度强化学习算法优点在于需要采样的数据少、算法效率高[19]，这种特点适用于车载计算平台。在DDPG 算法中有演员和评论家2个网络，演员网络近似表示策略函数，其输入为状态s，输出为动作a，表示为：

为了保证确定性策略的探索性，需要在策略动作中加入噪声ψ，则策略函数为：

评论家网络用来近似价值函数，输入为状态s和动作a，输出为Q值。评论家网络采用最小化损失函数来更新网络：

其中：

DDPG 中引入演员目标网络和评论家目标网络来提高训练的稳定性。目标网络的更新方式为：

Fujimoto[11]在DDPG 算法的基础上进行改进得到TD3算法。Fujimoto发现DDPG的算法中存在价值估计过高的问题，并引入DDQL 的思想将DDPG 中的式（15）改为：

式中，ε∼clip(N(0,σ),-c,c)为clip 参数；N(0,σ)表示期望为0，标准差为σ的高斯分布；c为目标平滑范围。

式（17）解决了DDPG的过估计和峰值故障问题，并对目标策略进行平滑处理。

此外，在TD3 中，演员网络的参数更新频率低于评论家网络的更新频率，降低了DDPG中由于策略的更新导致的目标变化所带来的波动性。

3.4 基于深度强化学习的能量管理策略

本文将深度强化学习算法应用在THS-Ⅲ平台PHEV 的能量管理中，智能体分别采用DDPG 和TD3算法，外部交互环境为车辆模型，整体框架如图5所示。

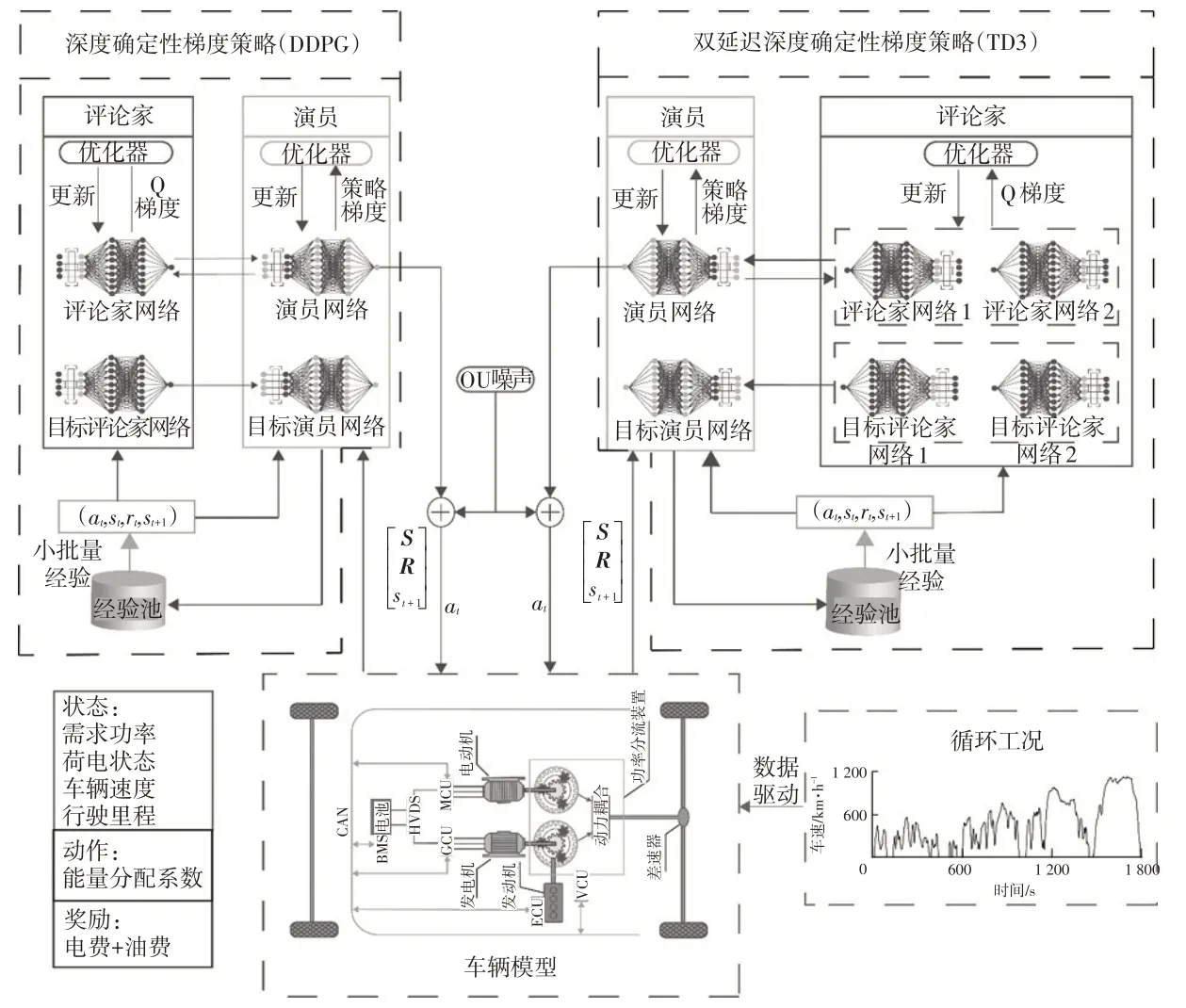
图5 基于深度强化学习的能量管理策略框架

马尔可夫决策过程中的状态、动作、奖励值的定义在基于深度强化学习的混合动力汽车能量管理中极其关键。

a.状态的定义。从算法的稳定性和收敛性角度考虑，本文仅选取较为关键的状态，状态S可表示为：

式中，v为车辆速度；SSOC为荷电状态；d为车辆行驶里程。

b.动作的定义。前向仿真模型通过驾驶员模型控制踏板开度并计算当前总功率需求Pr，通过A={a=[η]T}将Pr分配给发动机和电动机：

式中，η∈[0,1]为功率分配系数。

c.奖励值的定义。奖励值决定马尔可夫决策过程的解，且影响收敛精度和收敛速度。强化学习算法的目标是获取最大的预期累计奖励值，本文设定即时奖励值为时间步长内燃油消耗量与电量消耗的总花费之和的相反数，即时奖励值r(s,a)为：

累计回报Gt为：

式中，mt为t时刻的燃油消耗量；pfuel为燃油价格；Et为t时刻的电能消耗量；pele为电价。

4 训练数据的准备

图6所示为数据训练过程：首先使用工况数据对控制策略进行离线训练，然后将训练好的策略下载到控制器中进行在线学习。

图6 数据训练过程

4.1 典型工况

新欧洲驾驶循环（New European Driving Cycle，NEDC）工况是一种经典的测试工况，但其测试有非常大的局限性，在新能源汽车的测试中尤为明显。GB 19578—2021《乘用车燃料消耗量限值》[20]规定使用全球统一轻型车辆测试循环（Worldwide Light-duty Test Cycle，WLTC）工况代替NEDC 工况。与NEDC 工况相比，WLTC 工况引入了更多的瞬态过程，匀速比例降低，加速和减速更为频繁，有利于评价车辆在瞬态工况和高速工况下的能源消耗和排放水平[21]。本文采用WLTC-Class3工况，如图7所示，主要参数如表2所示。

图7 WLTC-Class3工况

表2 WLTC-Class3工况主要参数

4.2 ACC-60工况

本文将车辆的自适应巡航控制（Adaptive Cruise Control，ACC）与基于深度强化学习的能量管理策略相结合，并设定巡航速度为60 km/h，提出一种新的工况，即ACC-60工况。相比于训练单纯的传统工况，与车辆真实功能的结合将促进基于深度强化学习的能量管理的实际应用。

本文通过MATLAB 中的自动驾驶工具箱建立相关的道路和车辆环境。通过Simulink搭建ACC算法，并将巡航速度设置为60 km/h。该环境与控制算法能够较好地还原车辆在ACC状态下的速度变化情况。相关工况如图8所示，主要参数如表3所示。

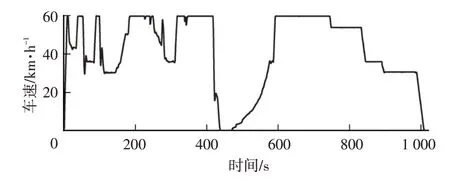
图8 ACC-60工况

5 仿真分析

通过WLTC-Class3 和ACC-60 工况对基于深度强化学习的能量管理策略进行仿真验证和结果分析。

5.1 算法验证

为了匹配工况和车辆的行驶数据，将仿真工况设定为2 个WLTC-Class3 循环和5 个ACC-60 循环。图9 所示分别为WLTC-Class3和ACC-60在100个回合内的训练结果，可以看出，无论哪种工况和算法，加入层归一化均有助于算法的稳定和收敛。

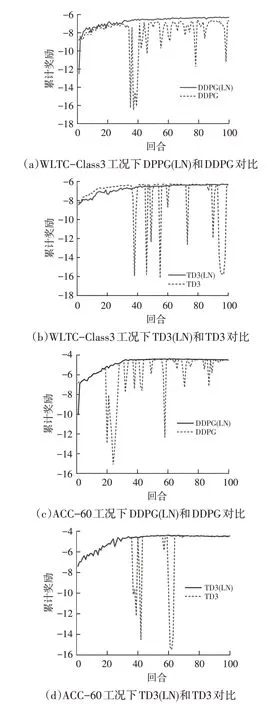
图9 不同策略和工况下的训练结果

图10 所示为在2 种训练工况下带有层归一化的双延迟深度确定性梯度策略（TD3(LN)）和带有层归一化的深度确定性梯度策略（DDPG(LN)）算法的对比。可以看出，二者在收敛过程和最终收敛值上区别不大。虽然TD3为DDPG的改进算法，但二者基本原理一致，TD3虽然有助于提高网络收敛的稳定性，但是在本文中DDPG也可以实现很好的收敛效果，而且DDPG相比于TD3拥有更为简单的网络架构，计算成本更低[11]。

图10 TD3(LN)和DDPG(LN)算法训练结果对比

5.2 仿真结果分析

图11 所示为2 种工况下不同算法的车辆SOC 随时间变化趋势的对比。可以发现，DDPG(LN)和TD3(LN)算法产生的变化趋势非常近似。另外，修改基于规则算法中的参数，使其SOC在[0.3,0.8]的范围内。

图11 2种工况下SOC随时间的变化情况

表4和表5所示分别为WLTC-Class3和ACC-60工况的仿真结果。以DDPG(LN)为例，可以得出，基于深度强化学习的能量管理策略在WLTC-Class3 工况下比基于规则的能量管理策略总花费节省了16.51%，燃油消耗量下降了15.56%，而在ACC-60 工况下比基于规则的能量管理策略总花费节省了31.95%，燃油消耗量下降了29.96%。在2 种工况中，与动态规划（Dynamic Programming，DP）算法相比，总花费差距仅为1.7%和0.4%。

表4 WLTC-Class3工况仿真结果

表5 ACC-60工况仿真结果

图12 和图13 所示分别为2 种工况下的电动机功率和转矩随时间的变化曲线。可以看出，基于深度强化学习的能量管理策略比基于规则的策略将更多的功率和转矩分配给了电动机，节省了燃油。另外，在动力电池能量超出安全范围被限制使用后，车辆可以利用制动能回收技术对动力电池进行充电，进一步节约费用。

图12 2种工况下电动机功率随时间的变化

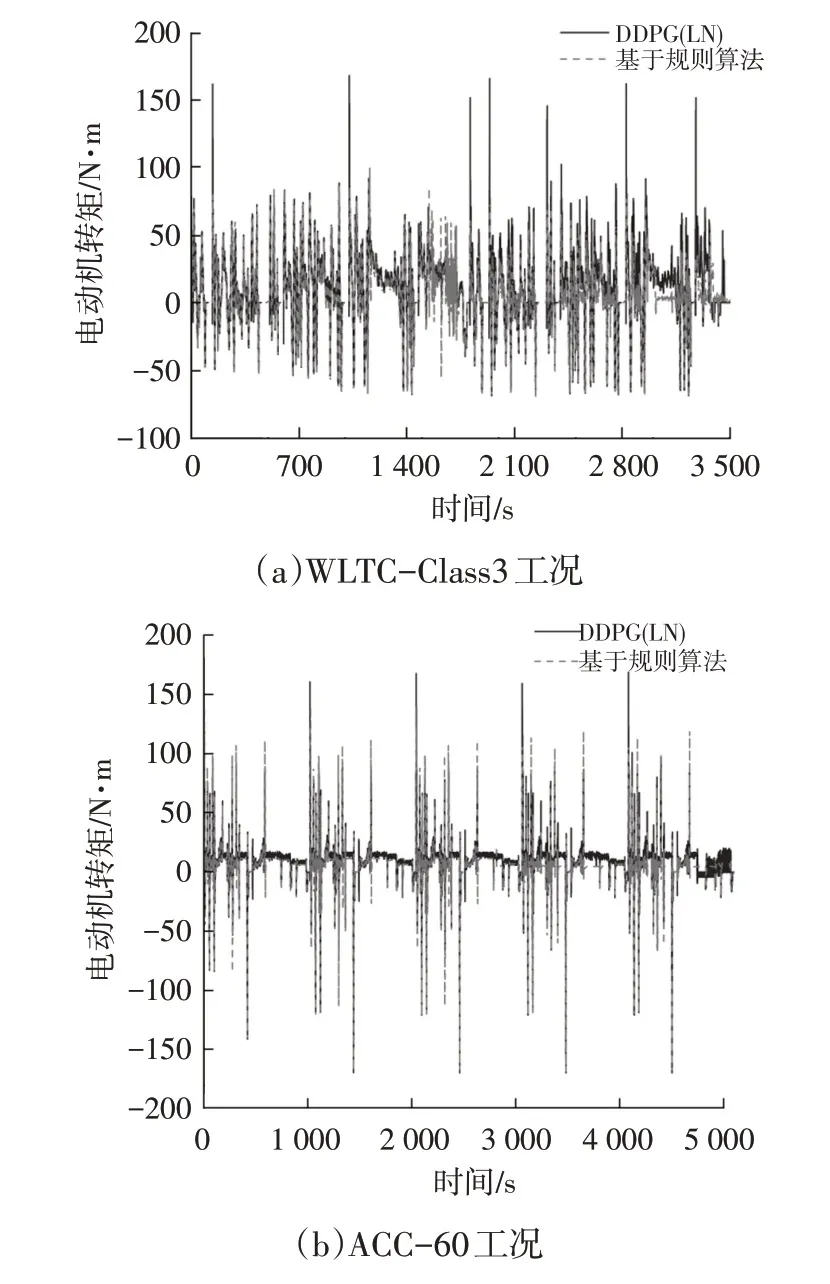
图13 2种工况下电动机转矩随时间的变化

6 结束语

本文基于MATLAB/Simulink 建立前向仿真车辆模型，通过对车辆能量管理MDP过程建模，将深度强化学习算法应用到THS-Ⅲ平台的混合动力汽车中，并得到如下结论：

a.加入层归一化的DDPG(LN)和TD3(LN)算法更加稳定，有助于算法的收敛。DDPG(LN)和TD3(LN)算法收敛数值和产生的策略非常相似，但DDPG(LN)的计算成本更低。

b.基于深度强化学习的能量管理策略不仅可以节省一定的费用，并且可以减少燃油消耗量，有助于保护环境。

c.在WLTC-Class3 工况下，DDPG(LN)和TD3(LN)算法都表现出很好的适应性。此外，2种算法在自行建立的ACC-60工况下也表现良好，表明其可以与车辆自适应巡航控制很好地结合，这将有助于基于深度强化学习的能量管理策略的实际应用。