基于田口法和响应曲面法的旋转唇密封可靠性分析*
张付英 夏靖炜 张志祥 马 骏
(1.天津科技大学机械工程学院 天津 300222;2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室 天津 300222)
旋转唇密封通常被称为油封,其作用是防止润滑油泄漏和外界杂质的侵入,具有结构简单、成本低、密封性好、追随性和补偿性好的优点,广泛应用于各工业领域的旋转轴密封。油封的可靠性不仅影响机械设备的工作效率、安全性和性能,而且油封失效会对环境造成影响并产生高昂的维修成本。油封的可靠性包括密封可靠性和损伤可靠性。通常将泵吸率和摩擦扭矩作为判断密封性能的指标,如果泵吸率大于0,说明润滑油从空气侧泵吸回油侧,油封处于密封状态;若泵吸率小于0,则油封会发生泄漏。摩擦扭矩则间接反映了密封运行时的摩擦热和磨损情况,摩擦扭矩越大,密封的可靠性越差。
随着现代机械的发展,对密封的要求也越来越高,国内外诸多学者已对旋转唇形密封的密封性能做了大量的实验和理论研究,并取得了丰富的研究成果。GABELLI[1]最先使用数值计算的方法来判断油封的密封性能。SALANT和FLAHERTY[2]建立了弹性流体力学耦合模型,在分析计算中考虑了唇口变形并引入空化指数,求解雷诺方程分析计算油膜压力,通过迭代法计算泵送率和摩擦力矩。STAKENBORG[3]建立了油封的二维模型,通过模拟计算得出接触压力与接触宽度呈正比,并且模拟结果与实验结果相符合。YANG[4]用MARC研究唇口的接触压力,并估算了油封唇口部位的油膜厚度。郭飞等人[5]建立了考虑流动因子的旋转唇密封混合润滑模型,预测旋转唇密封的最小膜厚、接触宽度、泵吸率和摩擦力矩。吴庄俊等[6]建立了简化的二维模型,得出抱轴力和接触宽度间的关系,并以此演算出包含转速和抱轴力的生热量和泵吸率方程,并分析了不同结构参数对唇形油封密封性能的影响。
国外有关密封圈可靠性的研究较少,目前国内对密封可靠性的研究主要是通过理论和计算机仿真对静密封展开可靠性研究。如于杨[7]给出了考虑接触压力和剪切应力的O形圈可靠性分析。陈永林和顾伯勤[8]建立了法兰密封垫片的泄漏干涉模型,并进行了垫片密封的可靠性计算。这些方法都采用应力-强度干涉模型对密封圈进行可靠度计算,但对动密封的可靠性研究较少。
由于泵吸率和摩擦扭矩作为可靠性指标的分析过程相似,为表示油封可靠性计算的完整过程,本文作者仅选择泵吸率作为可靠性指标,分析基于结构参数的旋转唇形密封的可靠度。文中油封的可靠性计算基于密封的极限状态方程。首先基于Abaqus有限元分析获得影响密封可靠性的结构参数,如理论接触宽度、前唇角、后唇角、过盈量、腰厚及其对应的静态接触压力;然后建立旋转唇密封的数值模型,计算不同结构参数作用下油封的泵吸率;其次应用田口法进行试验设计,确定各结构参数对油封密封性能的影响,应用响应曲面法建立油封的密封可靠性模型;最后应用蒙特卡洛法计算其可靠度。
1 旋转唇密封模型的建立
为了方便油封有限元分析和数值模型的建立与分析计算,做出以下假设:
(1)旋转轴和金属骨架的变形忽略不计;
(2)油封橡胶主体体积不可压缩;
(3)忽略运转后温度和油黏度变化等对密封性能的影响。
文中研究的油封为某变速箱输出轴的轴承密封,其结构为带有弹簧的内包金属骨架型,主体橡胶部分材质为丁腈橡胶,规格为60 mm×80 mm×8 mm,图1示出了旋转唇形密封的结构,唇与轴为过盈配合。油封的结构参数和工作参数如表1所示。
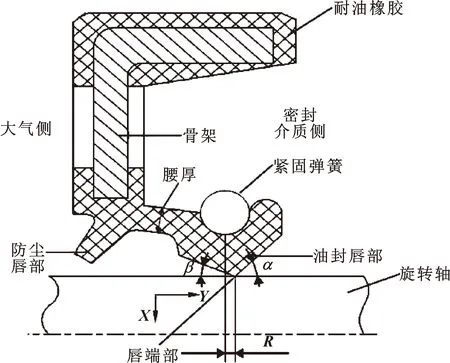
图1 旋转唇密封结构

表1 油封的基本参数
1.1 旋转唇密封的有限元模型建立与分析
有限元分析时,油封橡胶主体的IRHD硬度为75,其应力-应变关系为非线性,所以采用两参数的Mooney-Rivlin模型进行材料分析,材料常数可通过经验公式计算得出,C10=0.944 MPa,C01=0.236 MPa[9]。采用C3D8RH网格划分单元。由于油封的变形主要发生在唇尖部位,因此对此部分网格进行细化。建立的油封有限元模型和油封唇口局部细化网格如图2所示,并提取所研究结构参数下的静态接触压力和径向变形影响系数矩阵。
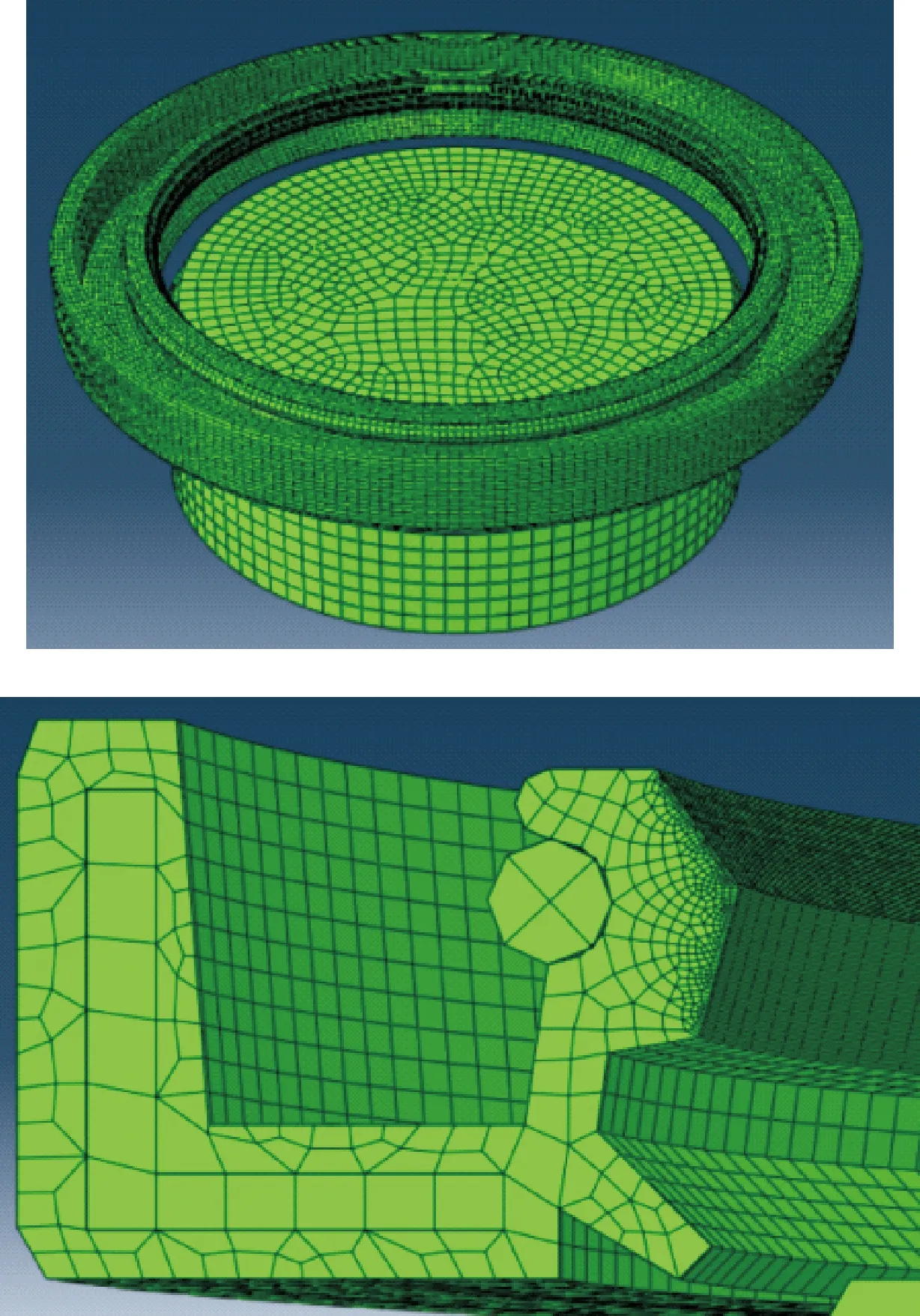
图2 油封的模型及局部网格细化
1.2 油封混合润滑模型的建立
油封密封区域的分布方向为轴向,因此文中基于式(1)所示的二维雷诺方程作为油封接触区润滑油膜的流体力学控制方程[10]。
(1)
式中:F为空化指数;Φ为流体压力/密度函数;H=h/σ,为量纲一油膜厚度,其中σ为油封表面粗糙度,h为油膜厚度;X=x/Lx,为量纲一周向坐标,Lx为圆周方向一个周期长度;Y=y/Ly为量纲一轴向坐标,Ly为实际接触宽度;K=Lx/Ly;V为量纲一旋转轴线速度,V=6μvLx/(paσ2),μ为润滑油黏度,v为油封的线速度,pa为环境压力;φx和φy为压力流量因子;HT为平均油膜厚度,可由式(2)计算。
(2)
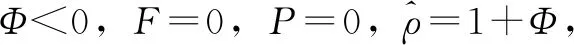
边界条件:在Y方向上,PY=0=Psealed,PY=1=1;
X方向P呈周期性变化,即,Px=0=Px=1,所有节点P≥0。
泵吸率Q[11]由式(3)计算得出。
(3)
油膜厚度可通过变形系统法计算,文中把油封一个周期Lx×Ly面积区域分为40×40个节点,节点i处的油膜厚度可通过式(4)计算。
(4)
式中:Hs为静态油膜厚度,其计算参考文献[10];In为量纲一径向变形影响系数,可由如图3所示的径向变形影响系数矩阵求得;Pavg是流体压力和接触压力总和,接触压力计算参考文献[11];psc为静态接触压力,由有限元分析获得。

图3 径向变形影响系数矩阵
如图4所示为静态接触压力曲线,油封数值计算流程如图5所示。
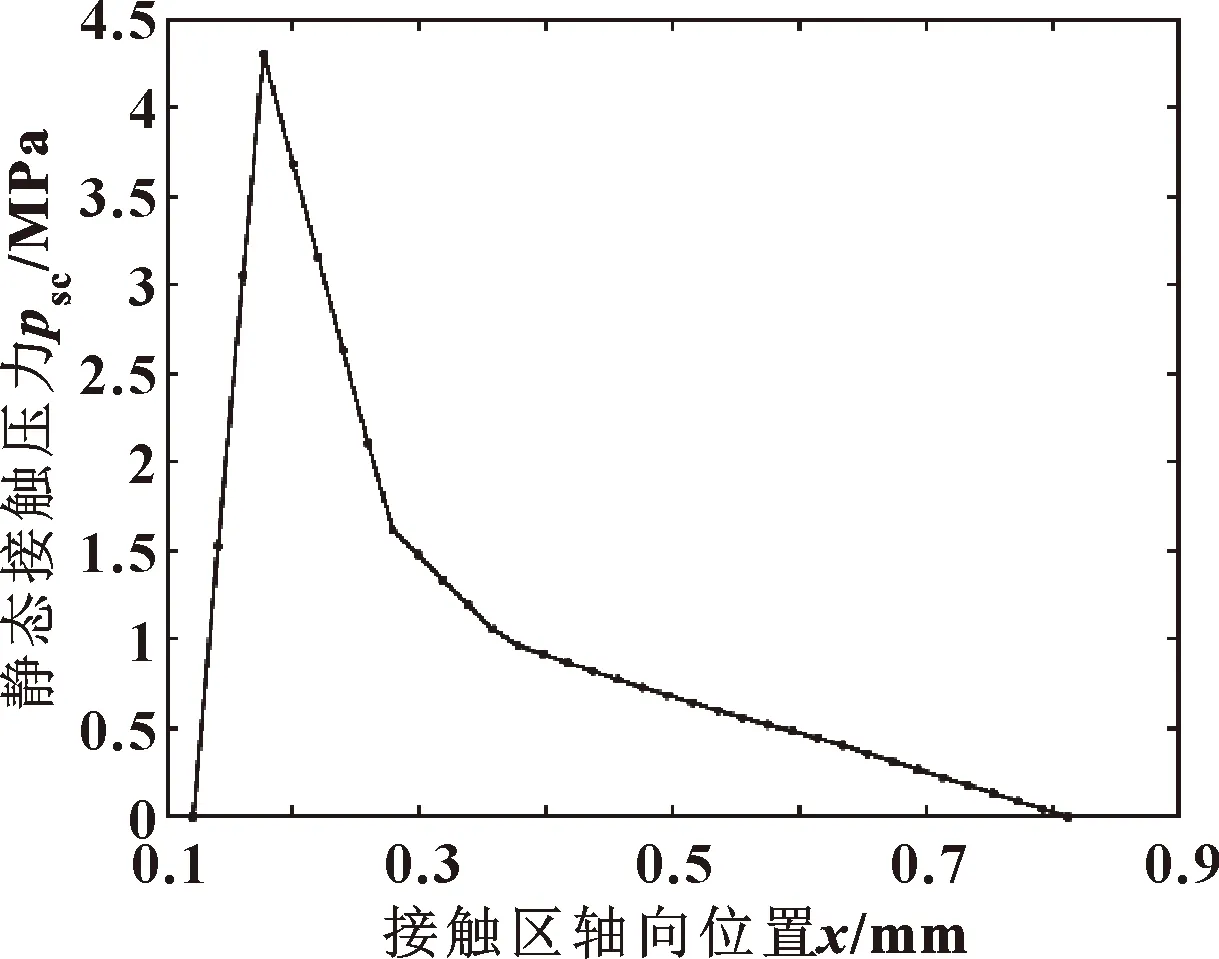
图4 静态接触压力分布

图5 数值计算流程
1.3 油封有限元模型和混合润滑模型的验证
基于建立的有限元模型和混合润滑模型,采用文献[5]中的结构参数及工况进行建模,提取数据并代入文中的数值模型进行计算,以验证数值模型的准确性,结果如表2所示。

表2 文献及文中数值模型计算的泵吸率对比
可以计算得出两者的相对误差在2%之内,证明模型有效。
2 基于田口实验法的油封密封可靠性因子分析
2.1 油封泵吸率的田口实验设计
为了研究油封结构参数对其密封可靠性的影响程度,利用田口方法的实验设计进行全因子正交试验,以油封可控因素中的理论接触宽度、前唇角、后唇角、过盈量和腰厚5个参数作为实验因子,以油封的泵吸率作为响应输出,以信噪比作为衡量泵吸率稳定性的指标,采用正交试验法获取各参数的较优组合,采用5因子3水平的正交试验,分析各因子对油封泵吸率的影响。表3所示为油封泵吸率的田口实验因子及水平,各因子的取值参考GB/T 9877—2008《液压传动旋转轴唇形密封圈设计规范》的推荐值范围确定[12]。
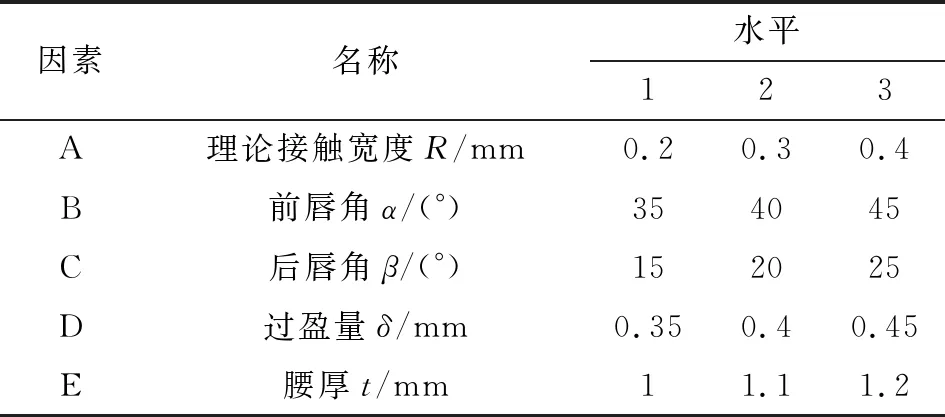
表3 田口实验的因子和因子水平
田口方法中,用信噪比作为衡量目标品质的指标,有望大、望小和望目3种特性,油封的泵吸率实验采用望大特性进行计算,即希望泵吸率越大越好。望大质量特性y的信噪比S/N的计算见式(5)。信噪比越大,说明在该参数水平下模型越稳定,油封的密封性能更好[13]。
(5)
表4给出了正交试验设计方案及信噪比,共安排27组随机试验。可见,第22组试验,即理论接触宽度为0.4 mm,前唇角为40°,后唇角为15°,过盈量为0.45 mm,腰厚为1 mm时稳定性最好。
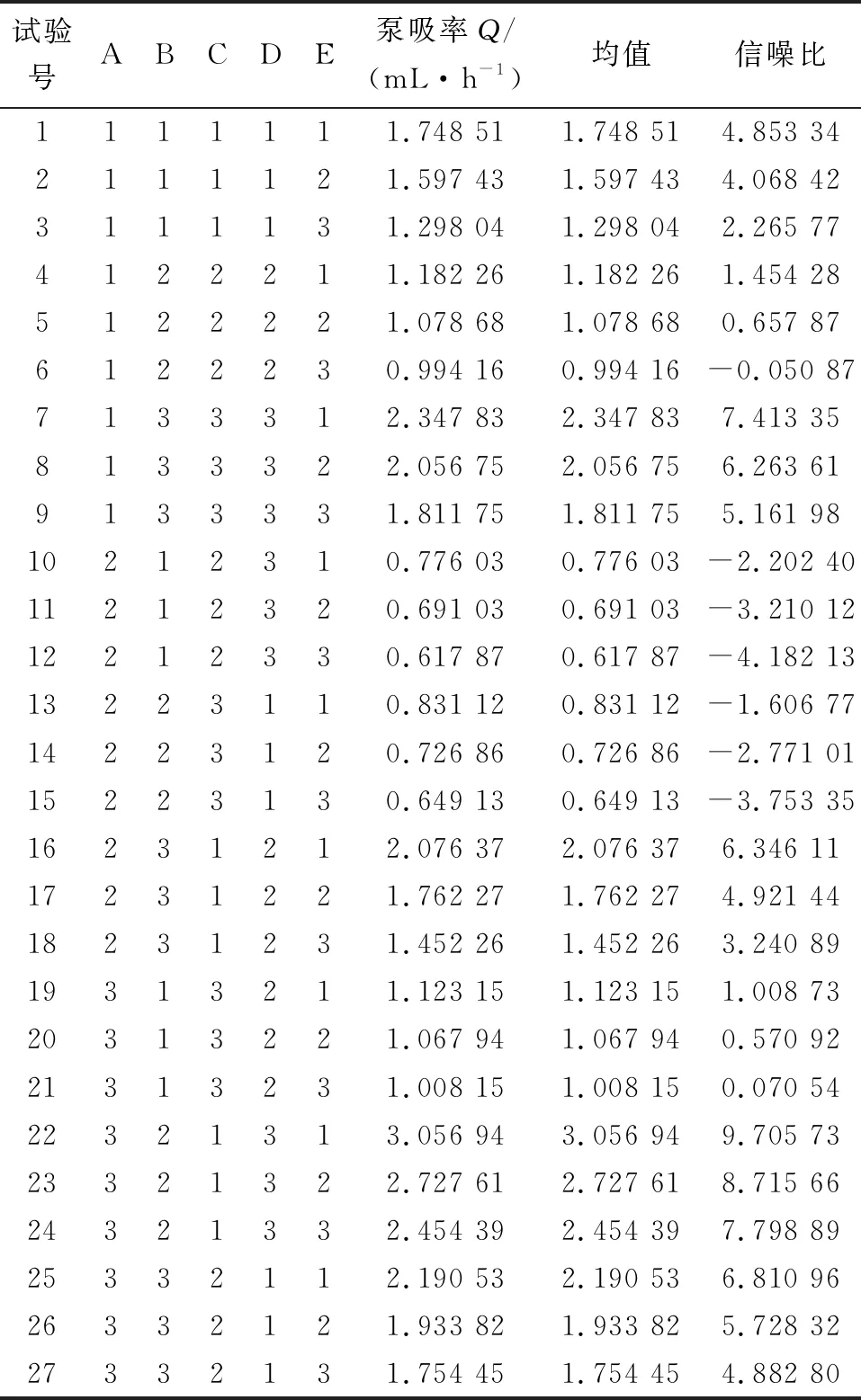
表4 正交试验设计及信噪比
2.2 基于田口实验设计的油封可靠性因子分析
Delta为信噪比的极差值,极差反映各个因子的重要程度,极差越大表明该因子的影响越重要。基于Minitab软件计算油封泵吸率的信噪比、均值的秩排序分别如表5和表6所示,通过秩的大小排序可判断哪一因素的影响最大。此外,信噪比和均值的主效应图(如图6所示)也可以直观判断各因素的显著水平。显然,对于信噪比而言,各个因子的显著水平由大到小依次为理论接触宽度、前唇角、后唇角、腰厚、过盈量;而对于均值,各因子的显著水平由大到小依次为理论接触宽度、前唇角、后唇角、过盈量、腰厚。该结果也可在主效应图中(如图6所示)得到验证。
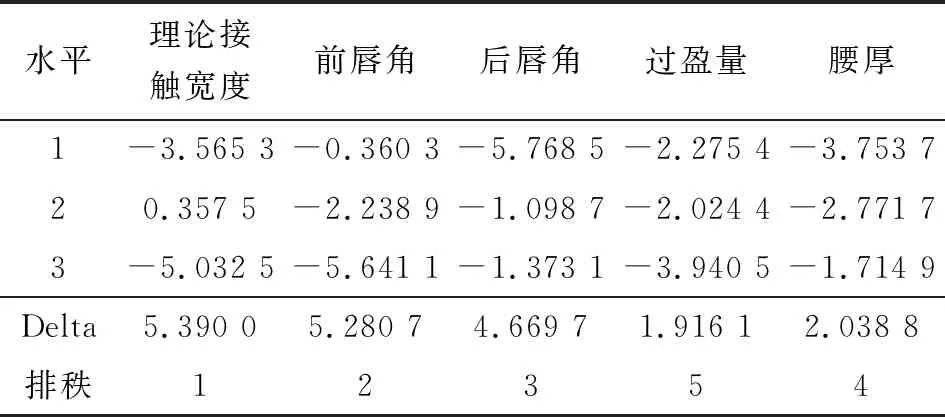
表5 信噪比排秩
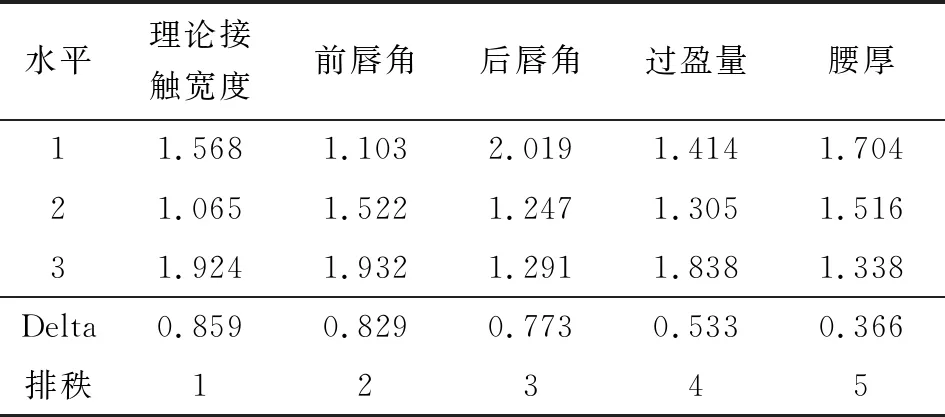
表6 均值排秩
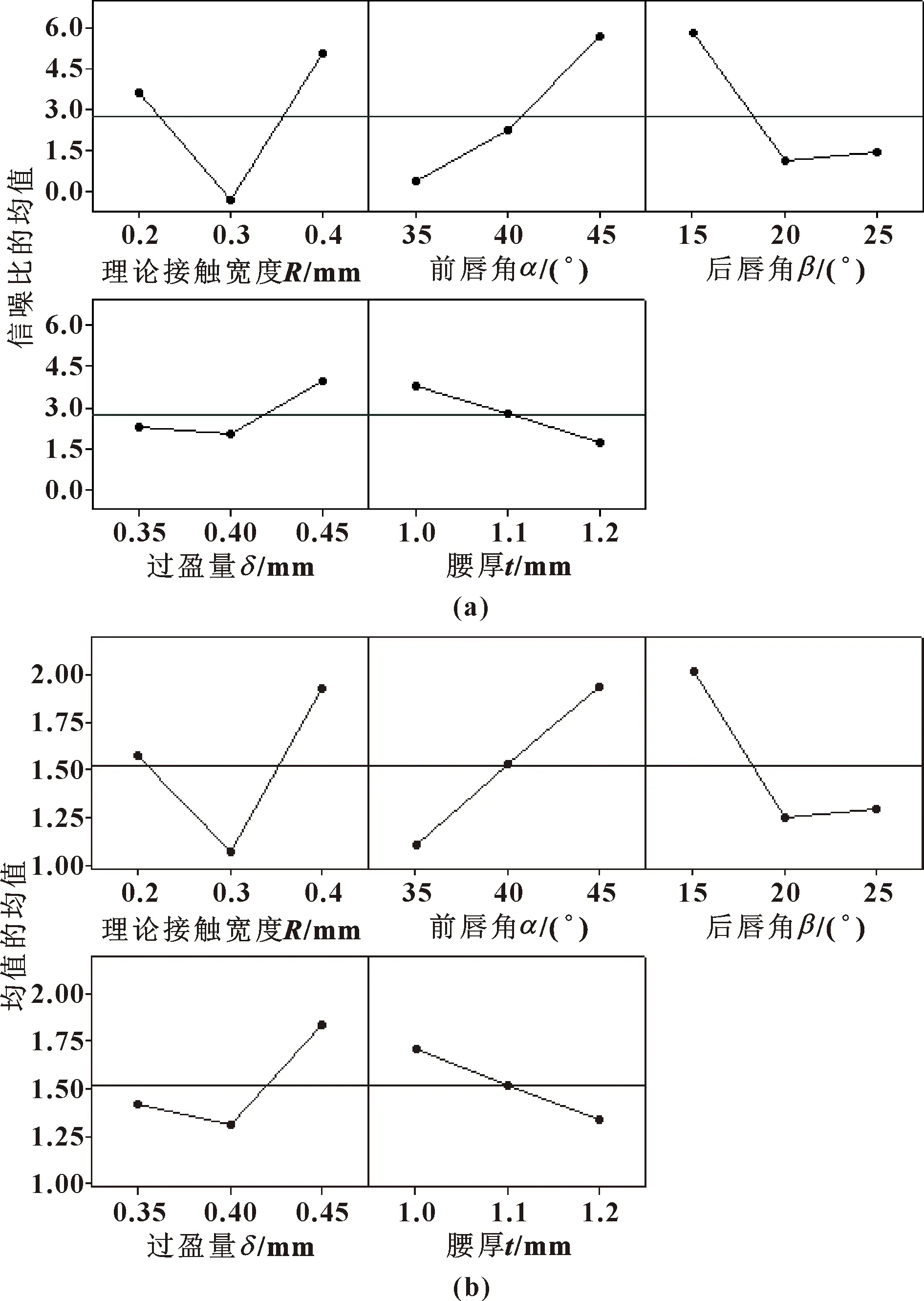
图6 信噪比主效应(a)和均值主效应(b)
3 基于响应曲面法的油封泵吸率函数拟合
3.1 油封泵吸率的模型拟合
响应面法是以综合实验技术为基础,通过拟合输出和输入变量的响应面来表示结构的真实失效面。响应曲面函数一般为非线性模型,如式(6)所示。
(6)
式中:a0、bi、cij为待定系数,可通过最小二乘估计或内插法进行确定。
非线性模型有线性+平方模型,线性+相互作用模型和完全平方模型。运用Minitab曲面分析对以上各个模型进行分析得到回归剩余标准差,分别为s=0.104 053,s=0.167 968,s=0.061 030 1,因此,选择完全平方模型的多元二次方程拟合回归函数,得到的泵吸率回归模型如式(7)所示。
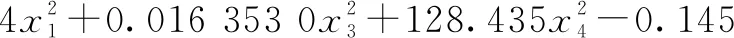
(7)
表7所示为泵吸率方差表,可见回归模型中各主效应和交互作用很显著(p≤0.05),表明模型拟合总体良好[14]。
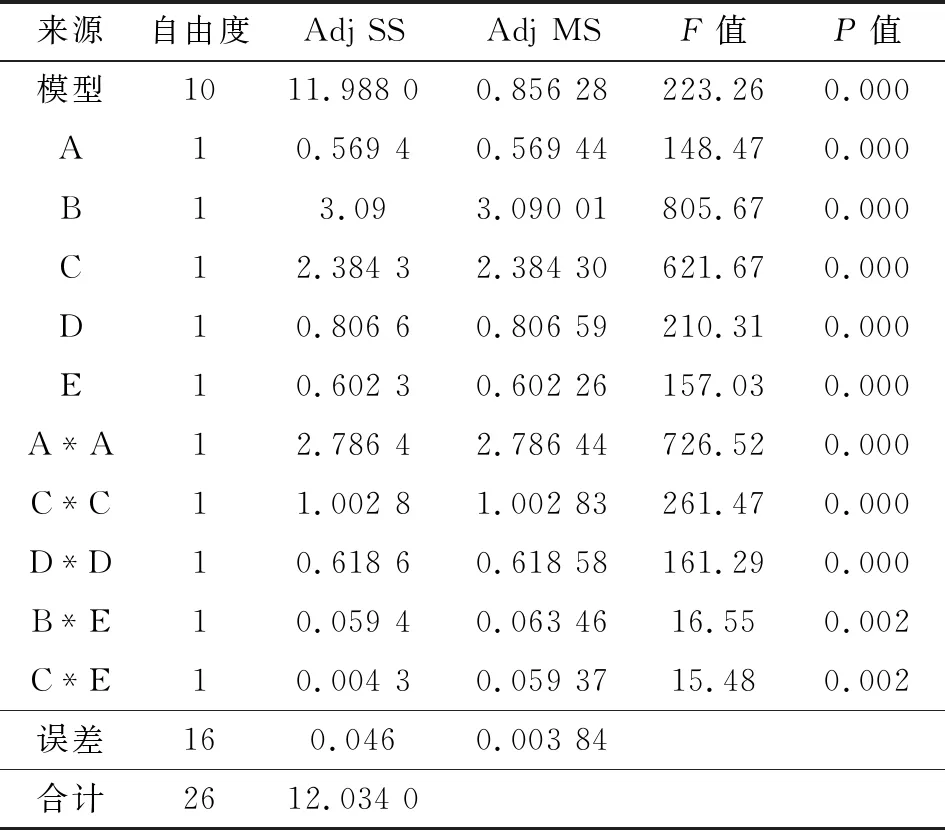
表7 泵吸率方差表
3.2 油封泵吸率拟合模型的诊断
通过如图7所示的泵吸率的残差分析来诊断所建立的模型。图7(a)、(c)所示的残差正太概率分布和残差直方图,说明模型的正态性假设成立;残差与响应变量拟合值的散点图(见图7(b)),没有呈现特殊的“漏斗形”或“喇叭形”[15],表明响应的拟合模型是正常的;残差以观测值顺序为横轴的散点图(见图7(d)),不存在0值线上下的异常波动,也不存在奇异点,表明数据的独立性合理。
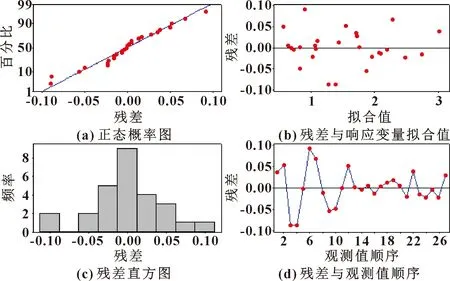
图7 泵吸率残差
4 油封的密封可靠性建模和计算
4.1 基于正态分布参数的油封可靠性建模
油封的密封可靠性可用可靠度来衡量,可靠度是指在规定的时间内和规定的条件下[16],油封实现其密封功能的概率,建立的油封可靠度模型如式(8)所示。
(8)
式中:R表示油封的可靠度;fX(X)为联合概率函数;g(x)表示油封的泵吸率极限状态方程,它表示油封的工作状态,当g(x)≥0时代表密封,反之,g(x)<0表示密封失效。
由于影响油封泵吸率的结构参数,均是在油封制作过程成形成的,因此假定其均为服从正态分布的随机变量,且各参数相互独立。依据随机参数矩阵X=[R,α,β,δ,t]T服从正态分布时,可靠性指标β的计算公式为
μZ=μR-μS
(9)
式中:μR表示变量的均值;σR表示变量的均方差;μS表示载荷效应的均值;σS表示载荷效应的均方差;μZ表示总均值;σZ表示总均方差。
得到可靠度的估计量如式(10)所示。
R=Φ(β)
(10)
式中:Φ(·)为标准正态分布函数。
4.2 基于蒙特卡洛法的油封密封可靠度计算
蒙特卡洛法是一种以统计学与概率论为基础的随机模拟法,是通过对变量随机取样的方法求其近似解,文中基于蒙特卡洛法计算油封的正态分布函数。具体过程为
假设功能函数为Z=g(x1,…,xn),由fx(x)模拟产生N组随机参数样本xj(j=1,2,3,…),代入结构功能函数求值,判断并统计落入可靠域的样本点数ns,用频率代表可靠度:
(11)
Ps=ns/N
(12)
对油封的5个变量进行随机化取样,然后代入结构功能方程计算,通过MatLab编写模拟蒙特卡洛概率程序。为了确保实验的准确性,N值越大越好,文中取N=100 000。计算结果如图8所示,得出样本中使油封极限状态方程大于等于0的样本个数ns=99 987,小于0的样本个数nf=13,因此,所研究油封的可靠性概率Ps=0.999 87,失效概率为Pf=0.000 13。
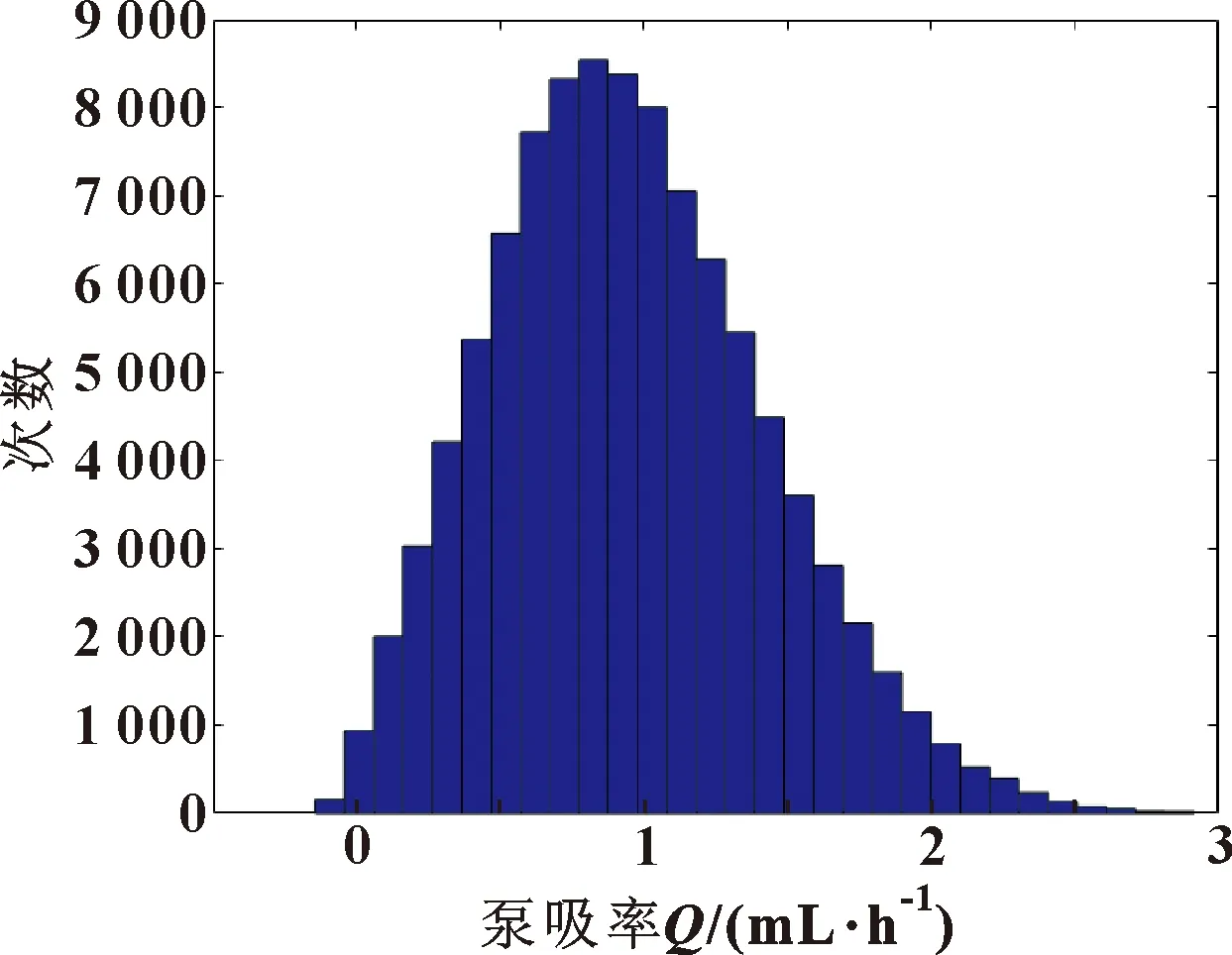
图8 泵吸率概率直方图
5 结论
(1)基于田口法进行正交试验,以信噪比作为衡量泵吸率稳定性的指标,在工况一定的情况下,分析各结构参数对泵吸率响应输出的影响程度。结果表明:对于信噪比而言,各因子的显著水平由大到小依次为理论接触宽度、前唇角、后唇角、腰厚、过盈量;对均值而言,显著水平由大到小依次为理论接触宽度、前唇角、后唇角、过盈量、腰厚;响应输出最大的参数最佳组合为:理论接触宽度0.4 mm,前唇角40°,后唇角15°,过盈量0.45 mm,腰厚1 mm。
(2)基于响应曲面法拟合极限函数,选取剩余标准差最小的作为函数模型;构建油封的可靠度模型,并运用蒙特卡洛法进行可靠度计算,计算结果可靠度为0.999 87。
(3)文中对给定结构尺寸的唇形密封进行可靠性分析,给出特定工况下的尺寸结构优化结果以及密封性能可靠度的计算结果,后续将继续考虑工况变化、材料老化等因素对密封可靠度的影响研究。

