随机变量及其分布单元测试卷（B卷）

■河南省临颍县南街高级中学 赵先举

一、选择题(本题共12 小题,每小题5分,共计60 分。在每小题给出的四个选项中,只有一项符合题目要求。)

1.在一次面试中,面试官从提前准备好的10道题目中抽出3道题让考生回答,若考生小张能回答其中6 道,则小张面试时恰好能正确回答2道题的概率为( )。

2.已知随机变量ξ～N(μ,σ2),若函数f(x)=P(x≤ξ≤x+3)的图像关于y轴对称,则μ=( )。

3.在一次课堂上,老师计划在班内随机选取一名学生回答问题,已知该班共有50人,其中女生20人,在女生中有6人住在306宿舍,则在回答问题的学生为女生的条件下,该学生来自306宿舍的概率为( )。

4.小赵在驾校一次通过科目二考试的概率是未通过的5 倍,令随机变量X=则P(X=0)=( )。

5.随机变量X的分布列如表1所示,若a,b,c成等差数列,且

表1

则P(X≥4)=( )。

6.甲、乙两人进行羽毛球比赛,比赛采取5局3胜制,无论哪一方先胜3 局比赛都结束,假定甲每局比赛获胜的概率均为,则甲以3∶1比分获胜的概率为( )。

7.已知随机变量X的分布列如表2所示。

表2

设Y=2X+3,则D(Y)等于( )。

8.设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )。

9.为喜迎“改革开放45周年”,某中学将于2023年5 月10 日在全校举行“改革开放知识”竞赛。在本次竞赛中共有40 道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的。评分标准规定:每题只选一个选项,答对得5分;不答或答错倒扣2分。某学生每道题答对的概率都为,则该学生在本次竞赛时得分的均值为( )。

A.96 B.132 C.172 D.186

10.某无人机配件厂商从其所生产的某种无人机配件中随机抽取了一部分进行质量检测,其某项质量测试指标值X服从正态分布N(18,4),且X落在区间[20,22]内的无人机配件个数为2 718,则可估计所抽取的这批无人机配件中质量指标值X低于14的个数大约为( )。

附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ≤ξ≤μ+σ)≈0.682 7,P(μ-2σ≤ξ≤μ+2σ)≈0.954 5,P(μ-3σ≤ξ≤μ+3σ)≈0.997 3。

A.228 B.455 C.27 D.40

11.若随机变量ξ～N(0,1),φ(x)=P(ξ≤x),其中x＞0,则下列等式成立的有( )。

①φ(-x)=1-φ(x);

②φ(2x)=2φ(x);

③P(|ξ|≤x)=2φ(x)-1;

④P(|ξ|＞x)=2-φ(x)。

A.①② B.②③

C.①③D.②④

12.多项选择题给出的四个选项中会有多个选项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。若选项中有i(其中i=2,3,4)个选项符合题目要求,随机解答该题时(至少选择一个选项)所得的分数为随机变量ξi(其中i=2,3,4),则有( )。

A.E(ξ2)+2E(ξ4)＜3E(ξ3)

B.E(ξ2)+2E(ξ4)＞3E(ξ3)

C.2E(ξ2)+E(ξ4)＜3E(ξ3)

D.2E(ξ2)+E(ξ4)＞3E(ξ3)

二、填空题(本题共4小题,每小题5分,共计20分。)

14.已知随机变量X～N(2,σ2),如图1 所示,若P(X＜a)=0.32,则P(a≤X≤4-a)=____。

图1

15.如图2,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体。经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X,则X的均值为_____。

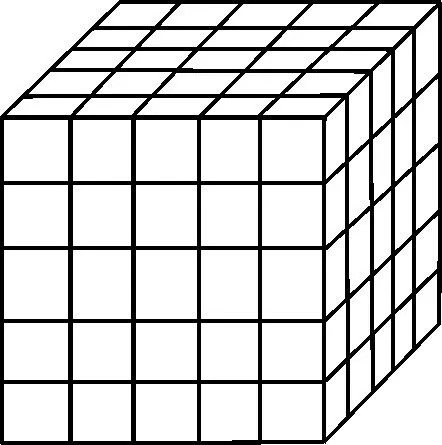
图2

16.盒中有2 个白球,3 个黑球,从中任取3个球,以X表示取到白球的个数,η表示取到黑球的个数。给出下列各项:

说法正确的项有____。(填上所有正确项的序号)

三、解答题(本大题共6小题,第17题10分,其他题每题12分,共计70分。解答时应写出必要的文字说明、证明过程及演算步骤。)

17.(本小题10 分)现有来自甲、乙两班学生共7名,从中任选2名都是甲班的概率为

(1)求7名学生中甲班的学生数;

(2)设所选2 名学生中甲班的学生数为ξ,求ξ≥1的概率。

18.(本小题12分)为了了解疫情后夜市经济推广效果,某地对夜市消费情况进行了一次随机调查,得到每次逛夜市的平均消费情况,如表3所示。

表3

(1)根据上表,估计男、女顾客每次平均消费大于50元的概率;

(2)若在夜市上随机选取一名男顾客和一名女顾客,记X为消费大于50元的人数,求X的分布列与数学期望。

19.(本小题12分)为做好党的二十大宣讲工作,某地从三所高校选取一部分大学生作为宣讲志愿者。已知来自甲高校的学生有12名,其中女生8 名;来自乙高校的学生10名,其中女生4 名;来自丙高校的学生9 名,其中女生3名。

(1)若从参与宣讲的学生中选取一人作为队长,求在选取甲高校学生的条件下,该学生为女生的概率;

(2)若从某一高校参与宣讲的同学中随机选取2人在网上进行直播,求这2人恰好是一男一女的概率。

20.(本小题12 分)某 贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众奔小康。经过奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加,为了制定提升农民收入的工作计划,该地扶贫办统计了2020年50位农民的年收入并制成频率分布直方图(图3)。

图3

(1)根据频率__分布直方图,估计50 位农民的年平均收入(单位:千元)(同一组数据用该组数据区间的中点值表示)。

(2)由频率分布直方图,可以认为该地区农民收入X服从正_态分布N(μ,σ2),其中μ近似为年平均收入近似为样本方差s2,经计算得s2=6.92,利用该正态分布,求:

①在扶贫攻坚工作中,若使该地区约有84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?

②为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1 000位农民。若每位农民的年收入互相独立,记这1 000位农民中的年收入高于12.14千元的人数为ξ,求E(ξ)。

P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3。

21.(本小题12 分)某校在2023 年4 月举行春季运动会,已知小赵同学在运动会定点投篮比赛项目中每次投篮命中的概率都为,且每次投篮是否命中相互独立。

(1)求该同学在3 次投篮中至少命中2次的概率;

(2)若该同学在10次投篮中恰好命中k次(k=0,1,2,…,10)的概率为Pk,k为何值时,Pk值最大?

22.(本小题12分)一个袋中分别装着20个标号为1的小球和10个标号为2的小球(所有小球除了标号,大小形状完全相同)。若从袋中随机取出一个小球,标号为1,则放回袋中;若标号为2,则不再放回,另补一个标号为1的小球放入袋中。在进行n次重复这样的试验后,记袋中所有小球标号之和为xn。

(1)求x2的分布列和数学期望。

(2)若xn的数学期望为E(xn)。

①求证:{E(xn)-30}为等比数列;

②求E(xn)。