基于Sigmoid函数的机器人鲁棒滑模跟踪控制系统设计

李 妮

(西安明德理工学院 通识教育学院，西安 710124)

0 引言

机器人作为现代工厂中的一种重要设备，其存在使一般工人不能从事简单的重复劳动，而由工业机器人实现了更为准确、全面、有效的现代化生产过程。为了保证机器人能够精准地完成工业生产工作，有必要对机器人的实时轨迹进行跟踪控制。机器人跟踪控制的最终目的是使得机器人的位置、速度等状态量与给定的理想参数一致[1-2]。在实际的跟踪控制过程中，尽量降低控制程序对机器人启动工作参数的影响，为此，设计了机器人鲁棒滑模跟踪控制系统。

鲁棒控制为：当控制系统存在参数不确定性或环境干扰时，闭环系统依然保持稳定。而滑模控制的基本原理是在给定的时间内，将系统置于任何位置的初始状态强制控制到预定的滑模表面，再利用此控制动作将系统的状态沿滑模表面滑回原点，进入稳定状态。现阶段对机器人跟踪控制系统进行了研究，文献[3]设计了一种基于逆动力学的机械臂鲁棒位置控制方法。分析机械臂的电机系统，采用转矩位置转换和反演滑模控制方法，设计逆动力学控制器，得到电机转矩控制函数以及与电机的当前位置信息，以此计算机械臂位置控制量，从而实现机械臂鲁棒位置控制，其鲁棒性能较强。文献[4]设计了基于D-H参数的M-DOF机器人建模、规划与控制系统，构建工业机器人设计中的运动学模型，建立D-H参数坐标系，对正逆运动学模型进行推导，利用五次多项式插值算法，完成关节空间的轨迹规划，结合直线插补算法，实现M-DOF机器人建模、规划与控制。该方法具有较好的应用价值。然而，上述系统在实际运行过程中无法同时兼顾机器人的鲁棒性和滑模转换状态，最终导致系统输出结果存在控制效果差、精度低的问题。

为了解决上述问题，引入Sigmoid函数。Sigmoid函数是一种连接函数，从统计学角度而言，Sigmoid函数遵循了正态分布规律，并且其误差项的平均值为0，具有同方差的特性。Sigmoid函数在机器学习中具有极其重要的地位，经常被作为一种用于将变量映射到[0，1]的阈值函数。设计基于Sigmoid函数的机器人鲁棒滑模跟踪控制系统。通过分析机器人超声采集传感器工作原理等效电路图和机器人状态观测器结构图，确定机器人轨迹跟踪控制目标，对机器人鲁棒滑模跟踪控制器进行改装。根据机器人的结构构建机器人数学模型，利用机器人传感器与状态观测器采集实时运行数据，计算机器人跟踪控制量，构建滑模运动与切换方程，完成滑模运动状态的切换，采用Sigmoid函数生成机器人鲁棒滑模控制律，实现机器人鲁棒滑模跟踪控制。通过上述设计，以期实现机器人的鲁棒滑模跟踪控制功能，并保证机器人的跟踪控制效果。

1 机器人鲁棒滑模跟踪控制硬件系统设计

在机器人内部装设UB500-18GM75型号的超声采集传感器，通过发光二极管工作状况判断传感器的采集情况，在机器人状态观测器中嵌入一组滤波器，提高数据观测精度。以DSPTMS32OF281型号的处理器为控制器的核心处理元件，实现控制算法。

1.1 机器人传感器与状态观测器

装设机器人传感器的目的是获取机器人与外界环境之间的位置信息，从而确定机器人轨迹跟踪的控制目标。而状态观测器的工作内容是确定当前机器人的工作状态，具体包括关节位置、姿态等。以获取机器人及环境位置信息为目的，装设UB500-18GM75型号的超声采集传感器，该设备具有两个发光二极管工作状况，其中红色LED常亮表示收集错误，闪烁表示精确超声波在TEACH-LLV工作方式下的暂停目标检测；黄色LED常亮表示目标在测量范围内，而闪烁则表示在TEACH-IN工作方式下执行超声检测任务。装设超声采集传感器的工作原理等效电路如图1所示。

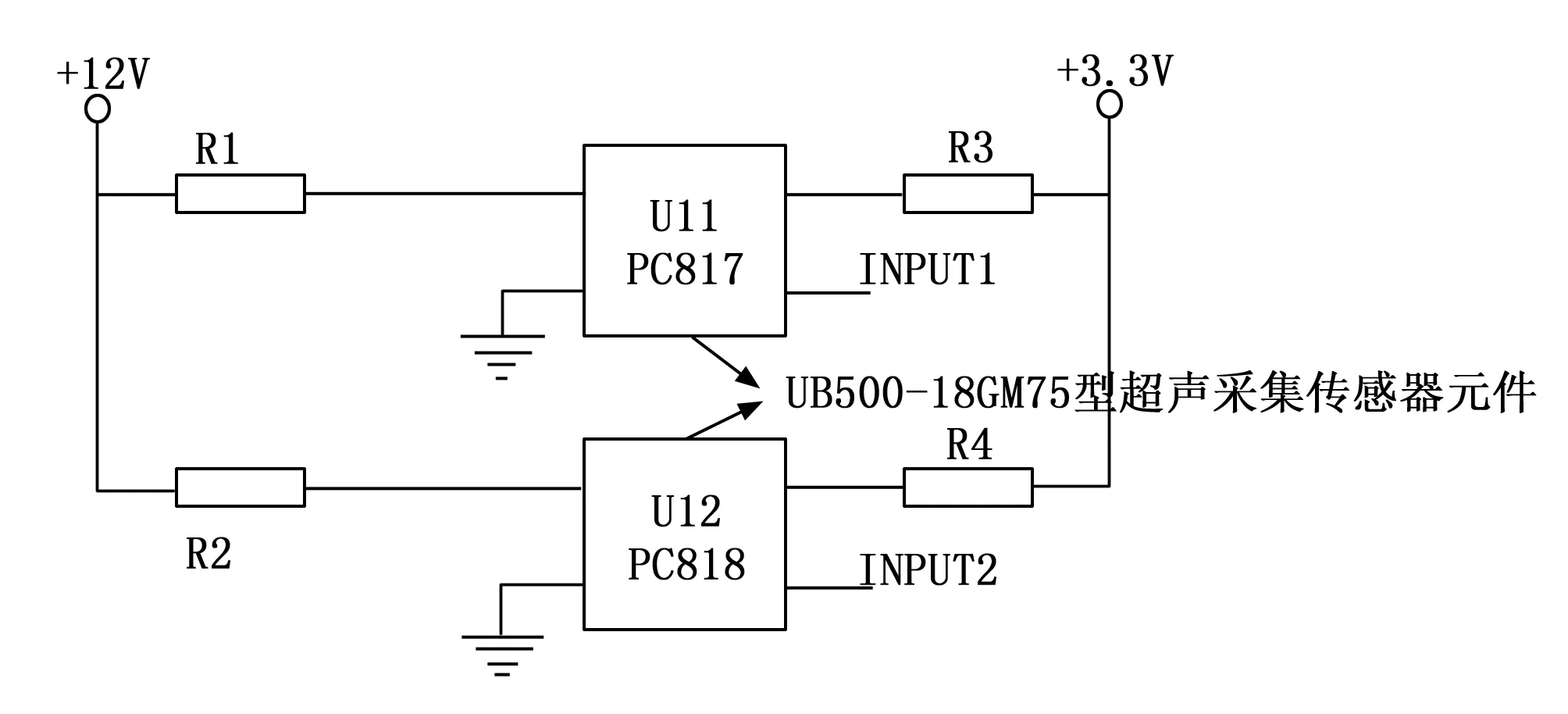
图1 机器人超声采集传感器工作原理等效电路图

在采集传感器的实际连接过程中，利用INPUTI ，INPUT2和OUTPUT连接LPC2119的相应引脚。在机器人超声采集传感器中嵌入一个无触点磁性转动编码器，可实现360度角的准确测量。集成的 Hall元件，模拟前端，以及数据信号的处理。将一个双极型磁体置于晶片的中央，构成了一种位置传感器。该位置传感器内置了 DSP处理器，它可以探测到磁场的方向，并且可以对12比特的二进制编码进行运算。另外，绝对角值也可以由脉冲宽度调制信号表示。另外机器人内置状态观测器的基本结构如图2所示。

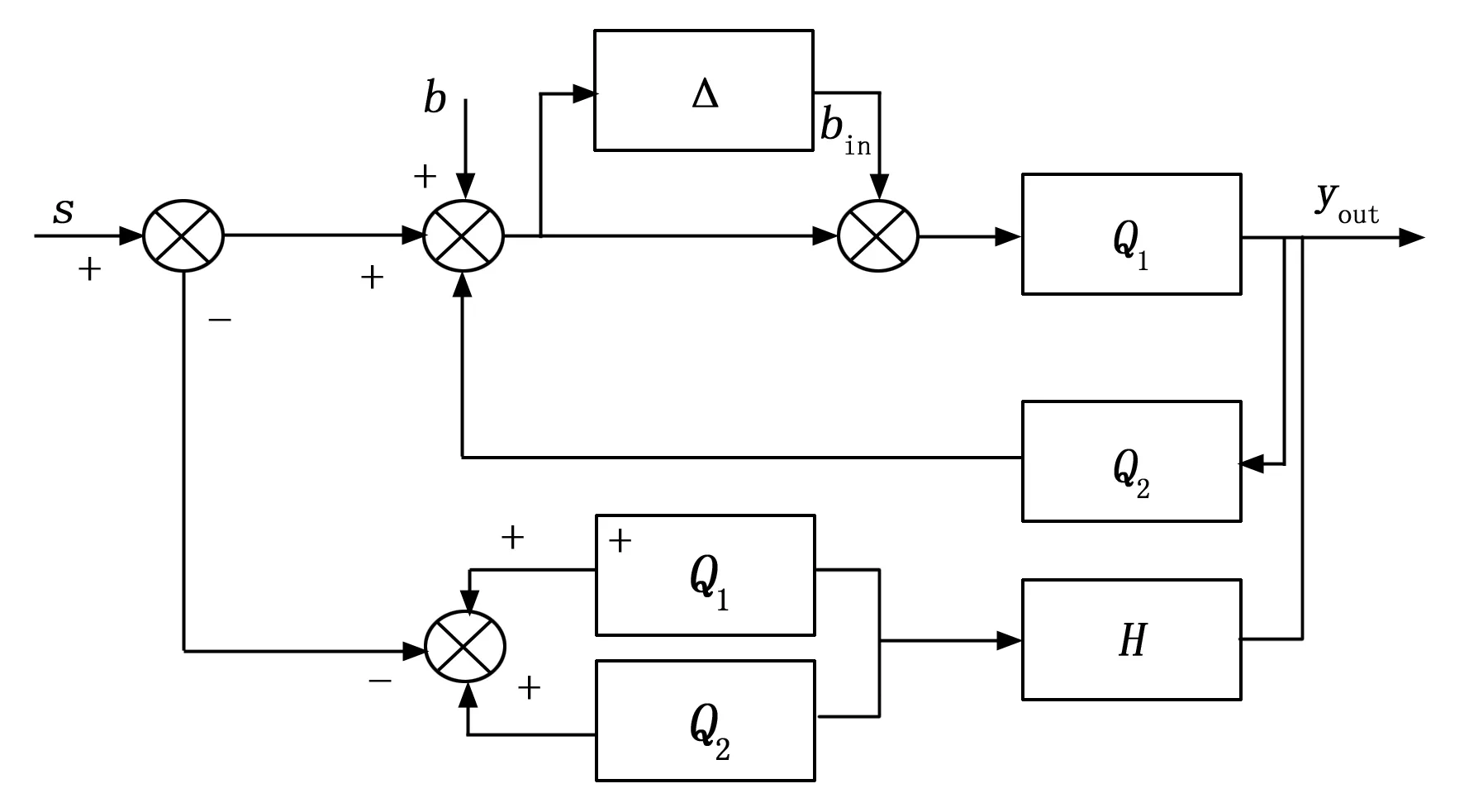
图2 机器人状态观测器结构图

图2中，Q1和Q2分别为机器人检测对象及其标称模型，Δ为机器人的乘法建模动态，b和bin对应的是机器人工作信号和未建模动态产生的等效信号，yout为机器人实时工作状态观测输出量。为了提高状态观测器输出的机器人状态数据的观测精度，在现有状态观测器的基础上嵌入了一组滤波器H。

1.2 改装机器人鲁棒滑模跟踪控制器

控制器是机器人鲁棒滑模跟踪控制功能的执行元件，鲁棒滑模跟踪控制器的改装结构如图3所示。

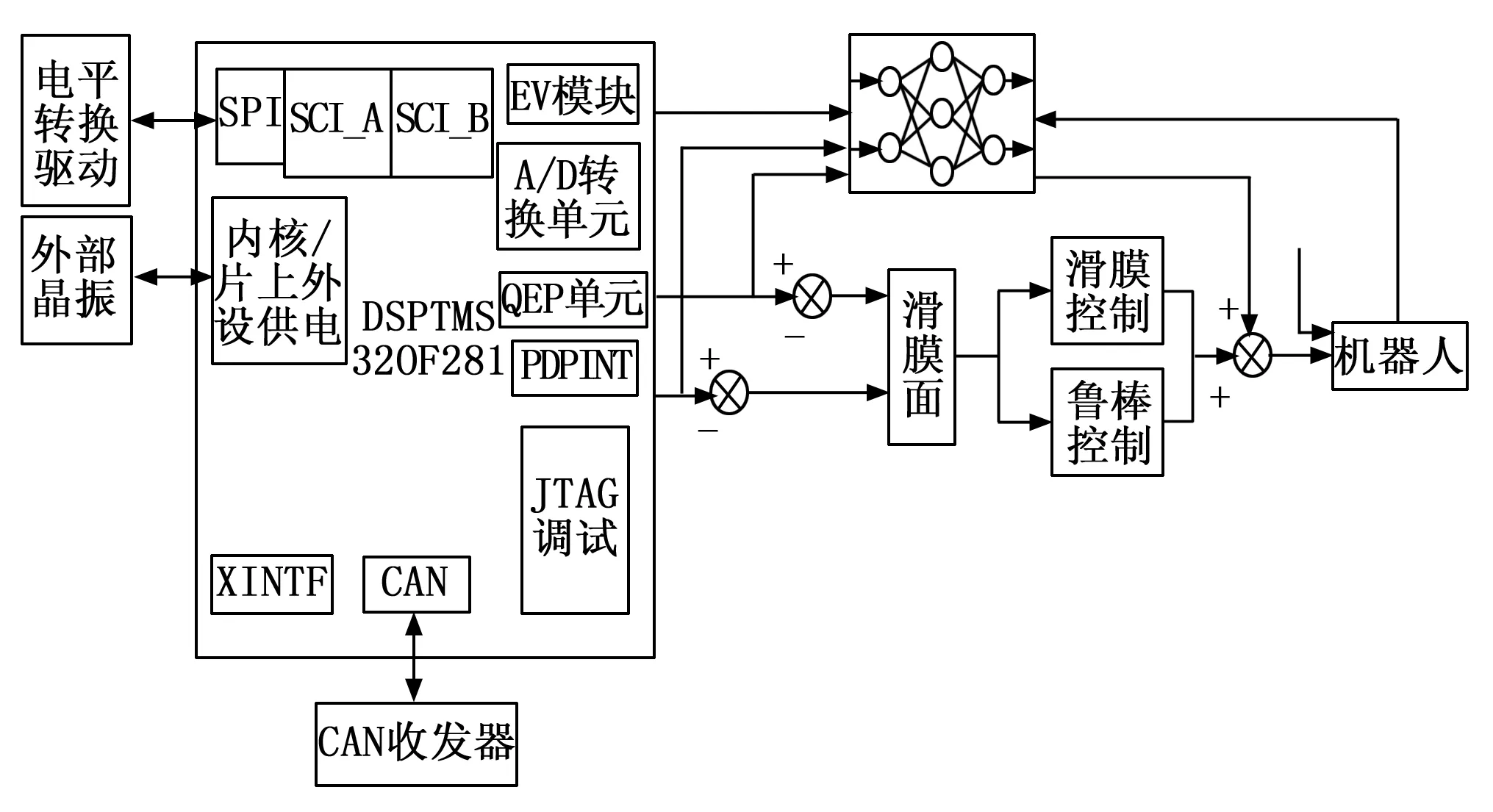
图3 机器人鲁棒滑模跟踪控制器结构图

从图3中可以看出，改装的鲁棒滑模跟踪控制器的核心处理元件为DSPTMS32OF281型号的处理器，负责实现控制算法并运行Sigmoid函数，为系统提供多种PWM控制信号。DSP芯片内部A/D变换，采集反馈信号，如电动机的电流、输出电压；当需要模拟量信号时，外延四路D/A变换器可以被指定：当输入到DSP时，过电流保护信号将会直接阻断切换管的驱动信号，当DSP接收到超过预先设定的限位数量时，DSP将会判断为长期过流，并且永久地关闭PWM信号直到人工恢复为止；在芯片上设置了一个正交编码的脉冲，它可以捕捉两个相位的差动输出脉冲，从而方便了速度和位置的控制[5]。另外，改装的控制器具备强大的数字通讯功能，内置了RS-232和RS-485通讯接口。通过RS-232通讯接口与主机通讯，上层机可以向驱动电机以及机器人关节发送命令。

2 机器人鲁棒滑模跟踪控制系统软件功能设计

分析机器人的结构，建立机器人运动学模型，进而获取机器人的数学模型，通过状态观测器采集机器人实时运行数据，根据机器人的各个关节的运动轨迹，计算机器人跟踪控制量，在趋近模态和滑动模态下，构建滑模运动与切换方程，利用Sigmoid函数生成相应的机器人鲁棒滑模控制律，获取机器人鲁棒滑模控制律的生成结果，通过积分隔离PID控制方法降低系统振动频率，提高系统的控制精度。

2.1 构建机器人数学模型

从结构方面来看，研究的机器人由执行、检测以及控制3个部分组成，其中控制部分主要用来发布控制任务，保证机器人可以在稳定移动的情况下完成既定任务[6]。在考虑机器人组成结构的情况下，结合机器人的运动原理构建相应的运动学模型如图4所示。

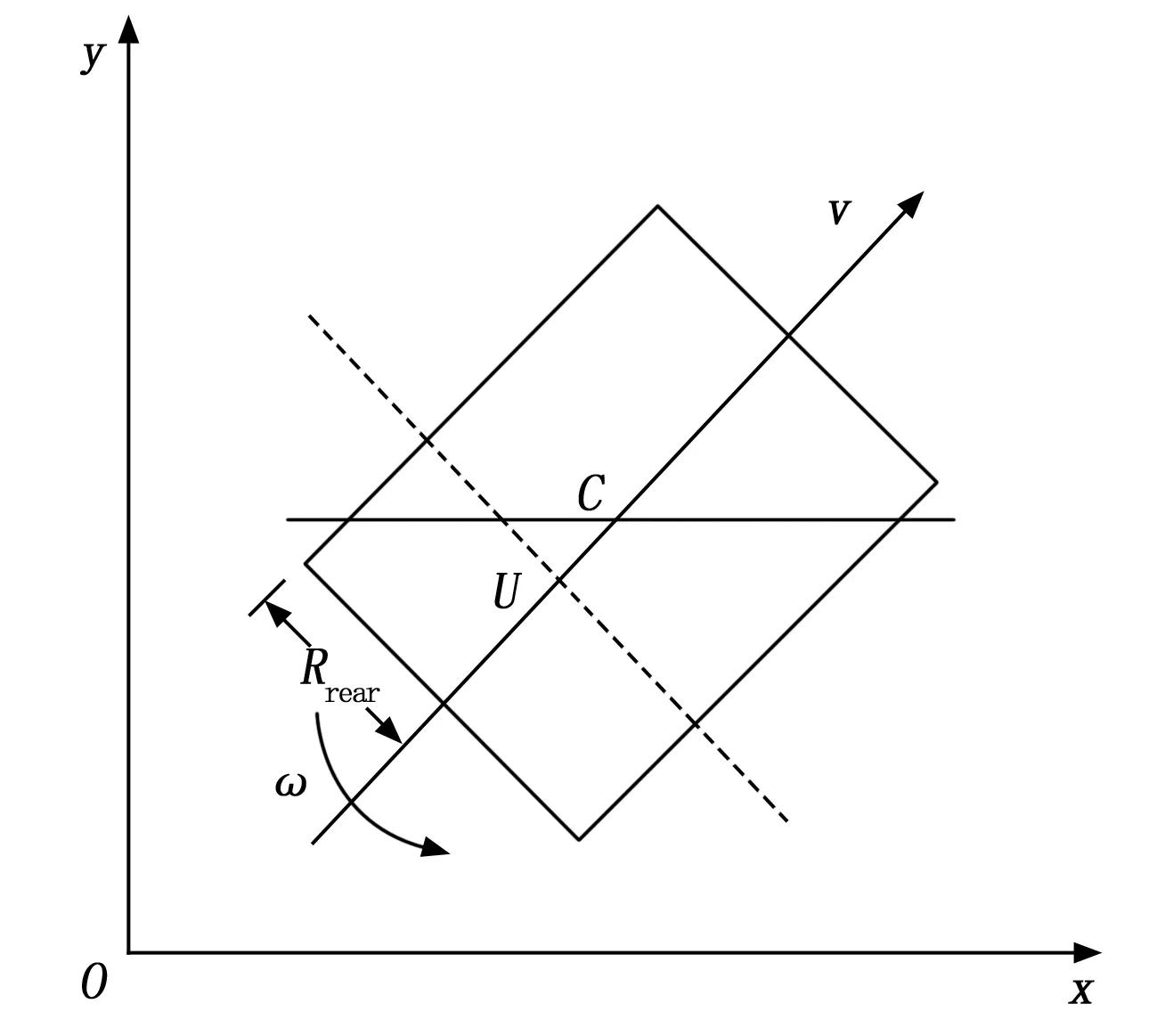
图4 机器人运动学模型示意图

图4中，参数U和C分别表示机器人后轴中心和质心，v和ω分别为机器人的实际移动速度和角速度，Rrear机器人后轮间距。在理想条件下，机器人实时转弯半径和横摆角速度可以表示为：

(1)

式中，Lf和Lwheel分别为瞬心到前轮距离以及质心与前轮垂直距离，θturn为前轮转向角，2dwheel表示的是前轮轮距，υr和υl分别为左、右轮轮速[7]。在设计实际机器人动态控制系统时必须考虑不确定性因素对控制品质的影响，确保系统的鲁棒性。在充分考虑不确定性因素，得到的机器人完整动力学模型如下：

(2)

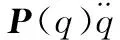
Zele=κeleΦIele

(3)

式中，变量κele和Iele分别表示常数系数和电机电枢电流，Φ表示通过直流驱动电机的单极磁通量。在机器人移动与执行任务过程中，各个关节驱动电机的转矩始终处于满足如下平衡关系：

Zele=Zf+Zload+Zinertia+μfω

(4)

其中：Zele为驱动电机的电磁转矩，也就是驱动设备的输出转矩，变量Zf、Zload和Zinertia分别为摩擦转矩、负载转矩和惯性转矩[9]。最终将驱动电机工作原理、动力学模型和运动学模型代入到机器人结构中，从而完成机器人数学模型的构建结果。

2.2 采集机器人实时运行数据

利用装设的机器人传感器与状态观测器，设置硬件设备的工作参数，传感器与状态观测器的输出结果即为机器人实时运行数据的采集结果，其中机器人状态观测器的实时输出结果可以表示为：

yout=htransmit(s)+htransmit(b)+htransmit(n)

(5)

其中，htransmit()为机器人状态信号在观测器中的传递函数。通过状态观测器的运行，得出机器人在任意时刻的位置信息以及运行速度信息。

2.3 计算机器人跟踪控制量

机器人跟踪控制量也就是当前机器人位姿与目标轨迹之间的偏差，根据机器人的执行任务生成各个关节的运动轨迹，标记各节点位置信息[10]。利用装设的机器人传感器与状态观测器，将当前机器人的实际运行状态表示为：

X(t)={[x(t)，y(t)]，v，ω，ϑ}

(6)

式中，[x(t)，y(t)]表示机器人的位置坐标，v、ω和ϑ分别为机器人的移动速度、关节角速度和关节角度，利用公式(6)可以得出机器人内各个组成元件在任意时刻的运行状态[11]。利用公式(7)计算当前机器人位置与输入轨迹中任意一点的距离。

(7)

式中，(xpi，ypi)为输入轨迹中第i个节点的坐标值[12]。选择d(j，pi)最小值对应的轨迹节点作为跟踪点，若公式(7)的计算结果为0，则表示机器人的坐标属于规划轨迹，即当前机器人处于规划轨迹上，否则认为机器人行驶轨迹存在偏差，那么机器人的跟踪控制量可以表示为：

(8)

其中：Δltrack和ϑtrack分别为移动距离控制量和关节角度控制量。按照上述步骤，即可得出机器人跟踪的实时控制量计算结果。

2.4 构建滑模运动与切换方程

机器人的运动模态包括趋近模态和滑动模态两类，到达滑模面之前的过程称为趋近模态，到达滑模面之后的运动过程称为滑动模态[13]。机器人滑动模态运动方程可以表示为：

Rslide=fslide(r，keq，t)

(9)

式中，r和keq分别为当前机器人的滑动状态和等效控制，变量r的取值分别为0或1，当r取值为0时证明当前机器人的运动模态处于趋近模态，否则认为机器人处于滑动模态。另外，fslide()表示的是为了达到全局滑模面设计的函数，其函数表达式如下：

fslide(0)=εspeed+Λ·Δltrack

(10)

其中：εspeed为机器人的速度跟踪控制量，Λ为正定矩阵[14]。将公式(8)的计算结果代入到公式(10)中，并与公式(9)进行联立，得出机器人滑动模态运动方程的构建结果，并通过对变量r的控制，实现滑模运动状态的切换。

2.5 利用Sigmoid函数生成机器人鲁棒滑模控制律

在改装鲁棒滑模控制器的支持下，根据机器人跟踪控制量的计算结果以及滑模运动与切换规律，利用Sigmoid函数生成相应的机器人鲁棒滑模控制律。Sigmoid函数也就是S型生长曲线，一般将其应用于神经网络中作为激活函数，取值范围在0～1之间。既可以映射实数、也可进行二分类，具有易于求导、平滑等特点，利用该函数对机器人实行鲁棒控制，可有效提升机器人的响应速度和控制精度。Sigmoid函数曲线如图5所示。

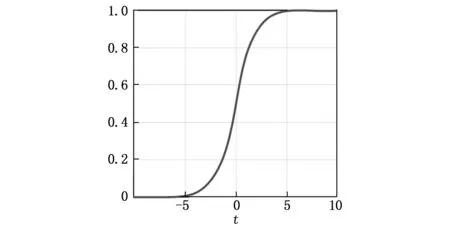
图5 Sigmoid函数曲线

机器人鲁棒滑模控制律生成过程中使用的Sigmoid函数表达式如下：

(11)

由于Sigmoid函数通常伴随神经网络一同运行，因此Sigmoid函数以神经网络作为运行背景[15]。假设在Sigmoid函数支持下，神经网络输出的机器人鲁棒滑模控制律为一维数据，则生成的机器人鲁棒滑模控制律可以表示为；

(12)

式中，Λ1和Λ2为对角正定矩阵，εi为神经网络输出的误差，误差函数对权值的偏导数分别为：

(13)

其中：ny为训练样本数，ϖj为神经网络的权重值，E为滑模控制误差集合。按照上述方法可以得出误差函数与神经网络中心以及宽度的偏导数计算结果，并对其进行实时更新[16]。在Sigmoid函数的支持下，保证生成的机器人鲁棒滑模控制律满足滑模的可达条件，并且通过选取合适的参数，能够保证系统在期望时间内到达滑模面[17]。为了保证改装鲁棒滑模跟踪控制器控制任务的执行力度，还需要利用Sigmoid函数以及神经网络进行控制律补偿，控制补偿量可以表示为：

(14)

其中：χj为Sigmoid函数的执行宽度。按照上述方式得出机器人鲁棒滑模控制律的生成结果，并通过改装控制器输出，直接作用在机器人执行元件上。

2.6 实现机器人鲁棒滑模跟踪控制功能

改装的机器人鲁棒滑模跟踪控制器能够执行常值切换、函数切换以及比例切换等控制任务，具体的控制原理可以表示为：

(15)

式中，u为输入到控制器中的机器人实时运行状态信号，sgn()为符号函数，λvss为机器人跟踪控制目标的最优解，λcon、λfun和λpro对应的是常值切换、函数切换以及比例切换的控制指令。与普通的跟踪控制相比，滑模跟踪控制的根本在于其控制的不连续性，当运动点运动到切换平面附近时，将从切换平面的两边同时趋向于该点，运动终止，由此可以定义机器人运动滑动模态区为：

(16)

其中：ξ为切换平面。在滑模区域内按照控制函数控制系统按照规定的状态运动，即实现了机器人的滑模控制。系统的滑模控制、鲁棒控制以及跟踪控制同步进行，利用改装的控制器生成滑模与跟踪控制指令，直接作用在执行元件上，在跟踪控制执行过程中，实时检测机器人的运行状态，光电编码器与减速器的输出轴相连，以实现伺服电机的位置回馈输出，并产生转速输出[18-20]。针对位置环，利用积分分块PID控制方法，在上位机的位置指示值与系统的位置反馈值有很大的偏差时，利用积分隔离PID控制的功能，既能有效地防止系统的振动，又能保证系统的控制精度。

3 系统测试与分析

为了验证所设计的基于Sigmoid函数的机器人鲁棒滑模跟踪控制系统的实际控制功能，设计系统测试实验。此次系统测试实验主要分为两个部分，一部分是测试在所设计控制系统下，机器人是否能够按照既定轨迹执行运动任务，另一部分是对比在有无环境干扰的情况下控制精度的变化情况。为保证所设计的机器人鲁棒滑模跟踪控制系统能够在实验环境中正常运行，需要对实验平台进行基本配置，实验平台的主控制器为百为公司的STM32开发板，系统上位机为LabBVIEW8.2软件、下位机为C语言。实验平台中的所有节点通过一对双绞线连接组成CAN通信网络，在所有硬件设备中集成串口以及CAN收发模块，保证各个硬件设备能够与上位机之间实现数据传输与通信。考虑到系统测试数据的复杂性，需要借助Matlab工具收集训练数据以及测试结果数据。

3.1 准备机器人样机

系统测试实验选择的机器人样机为IRB140型号的机器人，该机器人样机在出厂时包含两条机械臂和一个可移动的底座装置，每条机械臂中包含3个关节，分别为肩关节、肘关节和腕关节，每个关节的初始自由度设置情况不同。肩关节采用电机直接驱动，驱动电机型号为HC-KFS43，其转矩的额定值和最大值分别为1.3 N·m和0.85 N·m。腕关节和肘关节均采用同步轮同步带传动，转速比为8：1。在机器人的各个关节上安装编码器和传感器，编码器分辨率为120 000 p/rev。在开始系统测试实验之前，需要在实验环境中通过手动操作、远程传输等方式对机器人的功能进行测试，判断机器人样机是否能够在实验环境中正常运行，若存在功能运行异常的情况，需要对机器人元件甚至整机作替换处理。

3.2 生成机器人轨迹及鲁棒滑模跟踪控制任务

将生成直线轨迹、圆轨迹和曲线轨迹作为机器人的轨迹跟踪目标，在机器人的移动平台中任意选择两个点作为直线轨迹的起点和终点，根据两点确定一条直线的原理，生成机器人的直线轨迹。另外，圆轨迹和曲线轨迹的生成结果可以表示为：

(17)

式中，r为圆轨迹半径，φr为圆曲率，α为幅值参数。从公式(17)中可以看出，曲线轨迹的生成方式是模拟正弦运动。设定轨迹参数在0～8 mm之间，得出机器人轨迹的生成结果如图6所示。

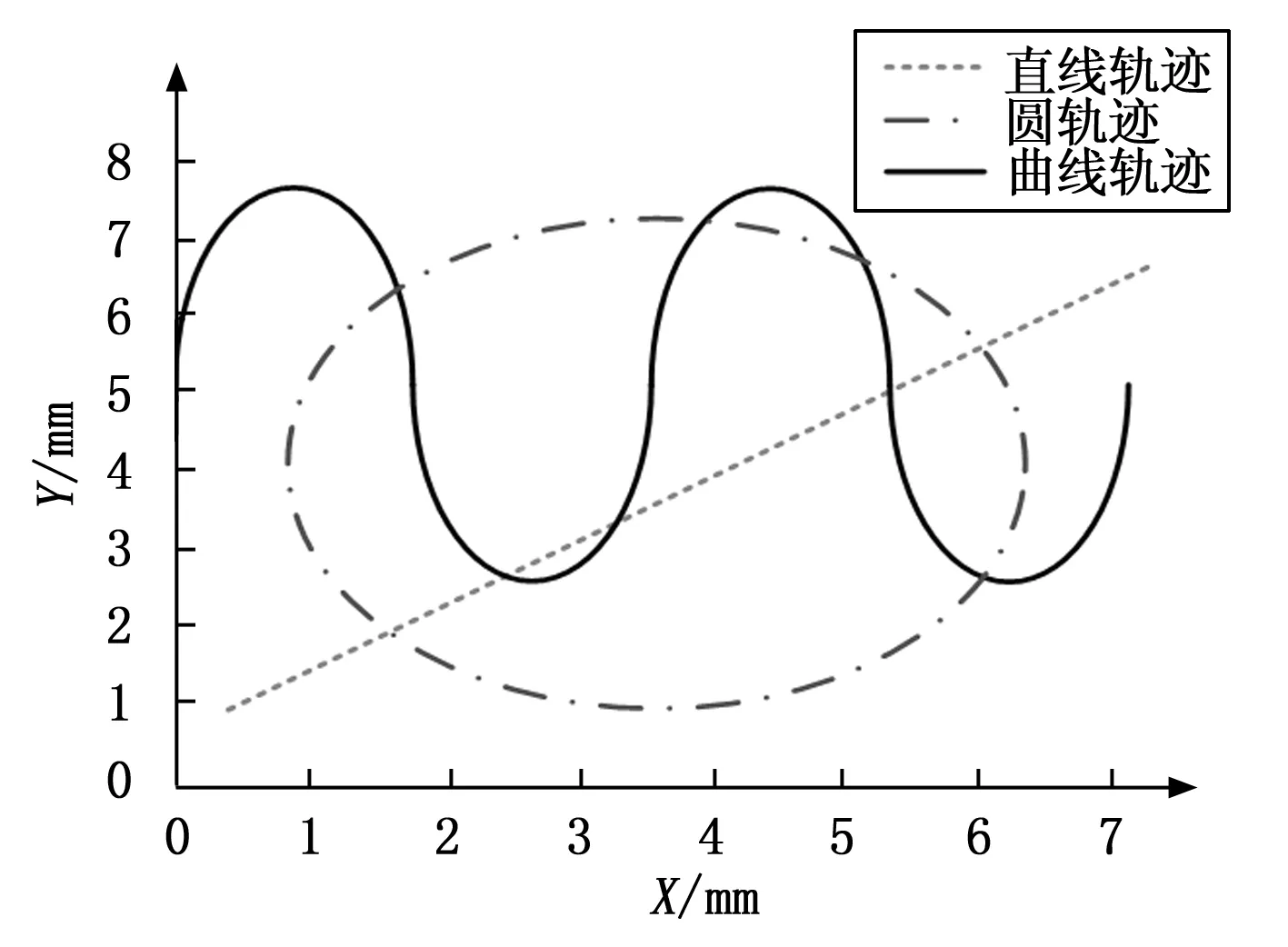
图6 机器人移动轨迹生成结果

对生成轨迹中的所有节点进行量化标记，作为机器人鲁棒滑模跟踪控制系统位置跟踪控制目标。除此之外还需要设置包含机器人姿态角、速度等信息的鲁棒滑模跟踪控制任务，部分控制任务的设置情况如表1所示。

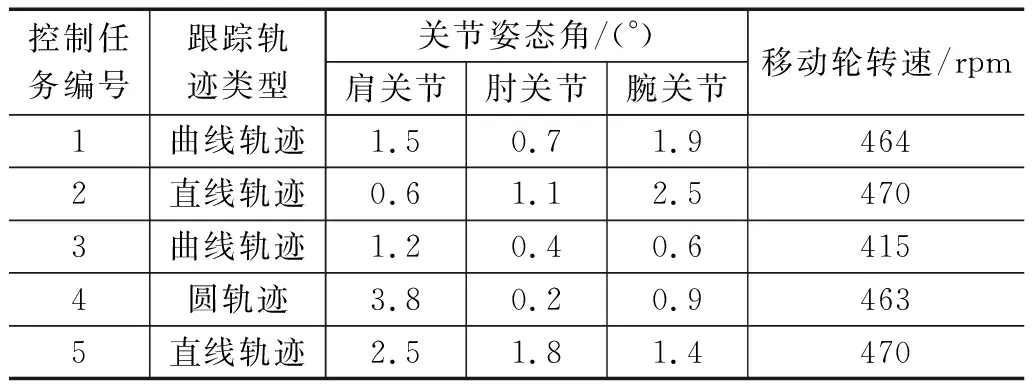
表1 鲁棒滑模跟踪控制任务设置表

由于机器人的位姿以及移动速度处于实时变化的状态，因此需要记录机器人任务执行状态下任意时刻的运动参数，以此作为验证机器人跟踪控制功能的比对标准。

3.3 加设机器人运行环境干扰器

在机器人的作业平台中加设一个干扰器装置，选择的干扰性型号为GRQ-03C，该设备通过发射无规律电磁信号实现对工作信号的干扰。设置环境干扰器的工作强度分别为0 dB和5 dB，从而实现对环境干扰的设置。

3.4 设置系统测试指标

根据系统测试实验目的，此次实验分别从机器人的轨迹跟踪控制精度和鲁棒控制效果两个方面进行，其中轨迹跟踪控制精度的量化测试指标分别为移动位置控制误差和关节姿态角控制误差，其中移动位置控制误差的测试结果为：

εposition=|xcontrol-xtarget|+|ycontrol-ytarget|

(18)

其中：(xcontrol，ycontrol)和(xtarget，ytarget)分别为机器人移动位置的实际值和目标值，根据表1的控制任务设置情况可以确定变量(xtarget，ytarget)的具体取值。同理，可以得出关节姿态角控制误差的数值结果如下：

εangle=|ϑi，control-ϑi，target|

(19)

式中，ϑi，control和ϑi，target分别为关节i姿态角的控制值与目标值。最终计算得出εangle和εposition的值越小，说明对应系统的跟踪控制功能越好。另外，系统鲁棒控制效果的测试指标设置为ι，该指标用来表示机器人在有、无干扰环境的情况下，控制误差的变化情况，该指标的数值结果为：

ι=|εposition，interfere-εposition|

(20)

式中，变量εposition，interfere表示在干扰环境下，机器人位置跟踪控制误差。在此次实验中，只考虑位置误差变化率，最终计算得出ι的值越小，说明对应系统的鲁棒控制效果越好。

3.5 系统测试过程与结果分析

由于所设计的机器人鲁棒滑模跟踪控制系统应用了Sigmoid函数，因此需要对相关的函数参数进行设置，并建立Sigmoid函数的运行环境。为了体现出所设计系统在控制功能方面的优势，分别设置文献[3]设计的基于逆动力学的跟踪控制系统和文献[4]设计基于D-H参数的跟踪控制系统作为实验对比系统，在相同的实验环境中对比3种控制系统，并保证系统的控制对象均相同。

3.5.1 机器人轨迹跟踪控制功能测试

将生成的机器人移动轨迹数据输入到所设计的控制系统中，进而生成对应的控制指令，在鲁棒滑模跟踪控制器的支持下，得出所设计控制系统的机器人移动轨迹，如图7所示。

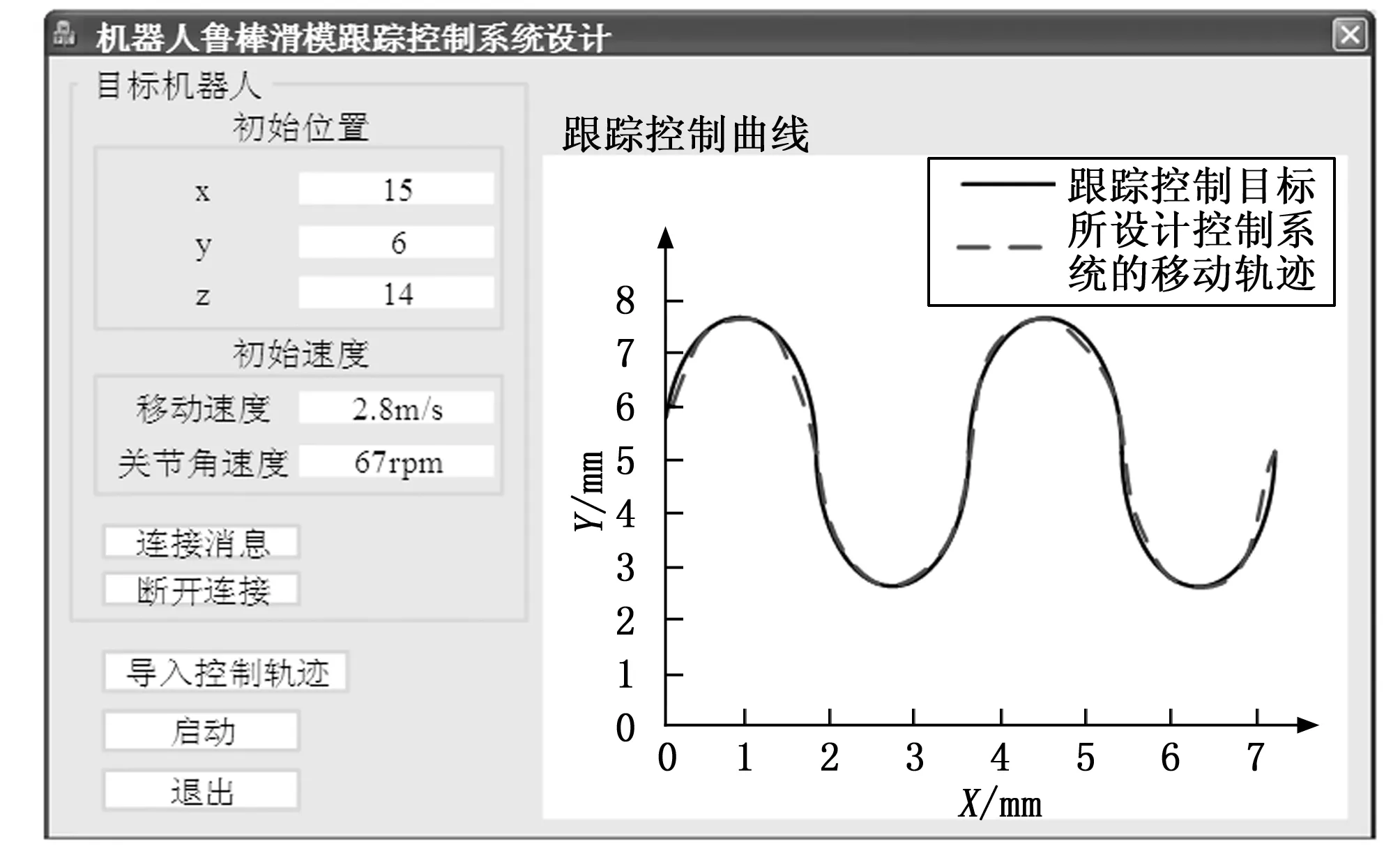
图7 所设计控制系统的机器人移动轨迹

同理可以得出文献[3]设计的基于逆动力学的跟踪控制系统和文献[4]设计基于D-H参数的跟踪控制系统的机器人移动轨迹，如图8所示。

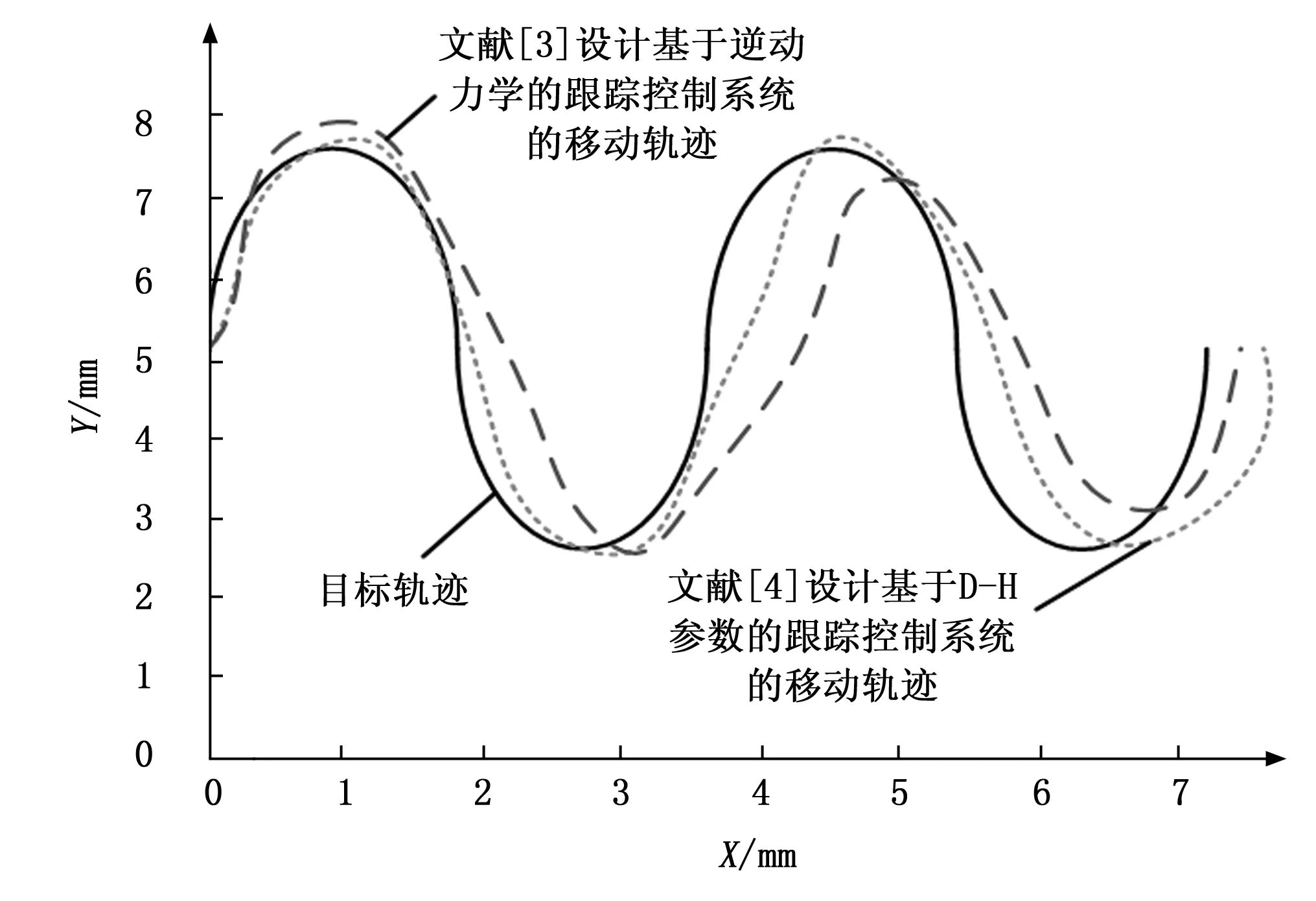
图8 对比控制系统的机器人移动轨迹图

从图7和图8中可以直观看出，所设计控制系统的机器人移动轨迹与设定轨迹目标基本重合，将机器人的实时位置信息代入到公式(18)中，计算得出文献[3]设计的基于逆动力学的跟踪控制系统和文献[4]设计基于D-H参数的跟踪控制系统位置跟踪控制误差的平均值分别为6.74 mm和5.85 mm，而所设计系统的平均位置跟踪控制误差为0.93 mm，低于文献[3]设计的基于逆动力学的跟踪控制系统和文献[4]设计基于D-H参数的跟踪控制系统的控制误差，证明所设计控制系统的轨迹跟踪控制功能更好。另外，机器人姿态角跟踪控制误差的测试结果，如表2所示。

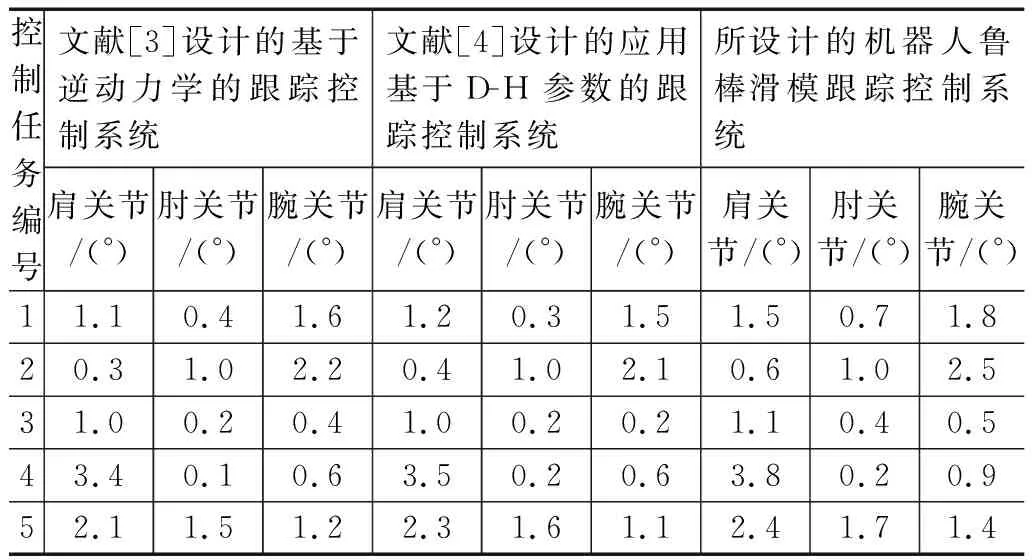
表2 机器人姿态角跟踪控制误差测试数据表

将表2中的数据代入到公式(19)中，计算得出3种控制系统的机器人姿态角跟踪控制误差的平均值分别为0.27°、0.26°和0.04°，由此可知，所设计控制系统的姿态角跟踪控制误差最小，轨迹跟踪控制功能好。因为所设计控制系统利用Sigmoid函数生成相应的机器人鲁棒滑模控制律，并通过积分隔离PID控制方法降低了系统振动频率，提高系统的控制精度。

综合上述实验结果可知，所设计控制系统的机器人移动轨迹与设定轨迹目标基本重合，其机器人姿态角跟踪控制误差平均值较小，能够有效提高机器人鲁棒滑模跟踪控制精度。

3.5.2 机器人鲁棒控制功能测试

将实验环境中的干扰器输出信号强度调整至5 dB，按照上述流程控制机器人，并得出相应的控制误差测试结果。将其与无干扰环境下的误差数据进行对比，得出系统鲁棒控制功能的测试结果，如图9所示。

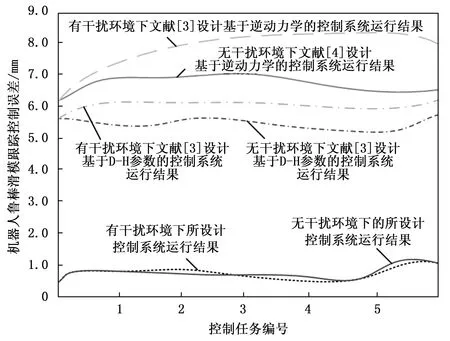
图9 机器人鲁棒滑模跟踪控制功能测试对比结果

由图9可以直观地看出，所设计控制系统的鲁棒滑模跟踪控制误差较低。通过公式(20)的计算，可得出文献[3]设计的基于逆动力学的跟踪控制系统和文献[4]设计基于D-H参数的跟踪控制系统的机器人鲁棒滑模跟踪控制误差的变化指数分别为0.34 mm和0.28 mm。而所设计系统的机器人鲁棒滑模跟踪控制误差的变化指数为0.06 mm，远远低于文献[3]设计的基于逆动力学的跟踪控制系统和文献[4]设计基于D-H参数的跟踪控制系统的控制误差，证明所设计控制系统的鲁棒滑模跟踪控制效果较好。

4 结束语

在实际的机器人使用中，为了实现对机器人的精准控制，设计了基于Sigmoid函数的机器人鲁棒滑模跟踪控制系统，保证了鲁棒精确跟踪运动轨迹。同时由于滑模在跟踪过程中与外界环境有较强的相关性，因此，根据其相关性进行了误差补偿，从而在保证鲁棒精准跟踪运动的同时，又不会影响到对环境的探测。从系统测试结果中可以看出，所设计系统可以实现对机器人实时、准确的控制，提高了机器人的跟踪精度，同时该系统可以对滑模跟踪的运行情况进行监测，使之保持高效稳定运行。