基于自适应并联结构神经网络的交通流量预测
杨启文,李 月,吴君娜,陈俊风,薛云灿
(河海大学 信息学部,江苏 常州 213022)
0 引言
随着社会的高速发展,城市交通流量持续增加,交通拥堵已常态化[1]。为了缓解交通拥堵、提高车辆的通行效率,实现交通智能化,交通流量的预测显得尤为重要。
由于车辆通行的随机性和复杂性,导致交通流量模型呈现具有极强的非线性特点,因此,通常采用利用非线性映射能力的人工神经网络(简称为“神经网络”)来建立交通流量预测模型,为智能交通提供决策依据[2]。例如,蒋杰[3]、赖锦辉[4]等人分别采用蚁群算法和布谷鸟搜索算法来优化BP神经网络,通过提高BP神经网络的逼近精度来建立更加精确的交通流量预测模型;Q.Chen,H.J.Yang以及W.Du等人则分别利用粒子群算法[5]、遗传算法[6]、鲸鱼算法[7]来优化小波神经网络(WNN,wavelet neural network),建立交通流量预测模型;Dogan通过长短时深度神经网络(LSTM,long short-term memory networks)来预测交通流量[8];在LSTM预测模型基础上,Lu进一步利用ARIMA模型组合来提高预测效果[9],而Jing则融合时间卷积神经网络(TCN,temporal convolutional network),构建了一种混合神经网络的交通流量预测模型[10]。
应用神经网络时,往往需要进行结构或参数优化,即神经网络训练。通常采用的训练手段有:采用试凑法[11],经验公式法[12],动态参数自调整法[13-14],模拟退火算法[15]和群智能优化算法[16]等方法来优化隐层节点数[17-18];采用梯度下降搜索法[19]、LM(Levenberg-marquardt)算法[20]、层次耦合约束优化算法[21]、模拟退火法[22]、群智能优化算法[23-24]等方法来优化神经元之间的连接权。
但是,在不同初始条件[25]下,即使采用具有全局优化能力的群智能算法和组合算法,也不能保证神经网络每次训练都能收敛到全局最优,从而导致神经网络的训练结果出现了一致性问题[26-28]。
为了增强训练结果的一致性、降低训练次数,提高工程应用的便利性,本文提出一种自适应并联结构神经网络(APSNN,adaptive parallel structure neural network),旨在采用常规优化算法,通过神经网络的自组织行为,在训练中实现网络结构自适应和参数优化;在满足训练精度前提下,维持训练结果的一致性。同时,利用APSNN,建立交通流量预测模型,降低预测偏差,提高预测的平稳性。
1 自适应并联结构神经网络
神经网络种类很多,本文考察常见的前向神经网络。
多层前向神经网络如图1所示,包括输入层、隐藏层和输出层,除输入层和输出层只有一层外,隐藏层可以是一层也可以是多层。
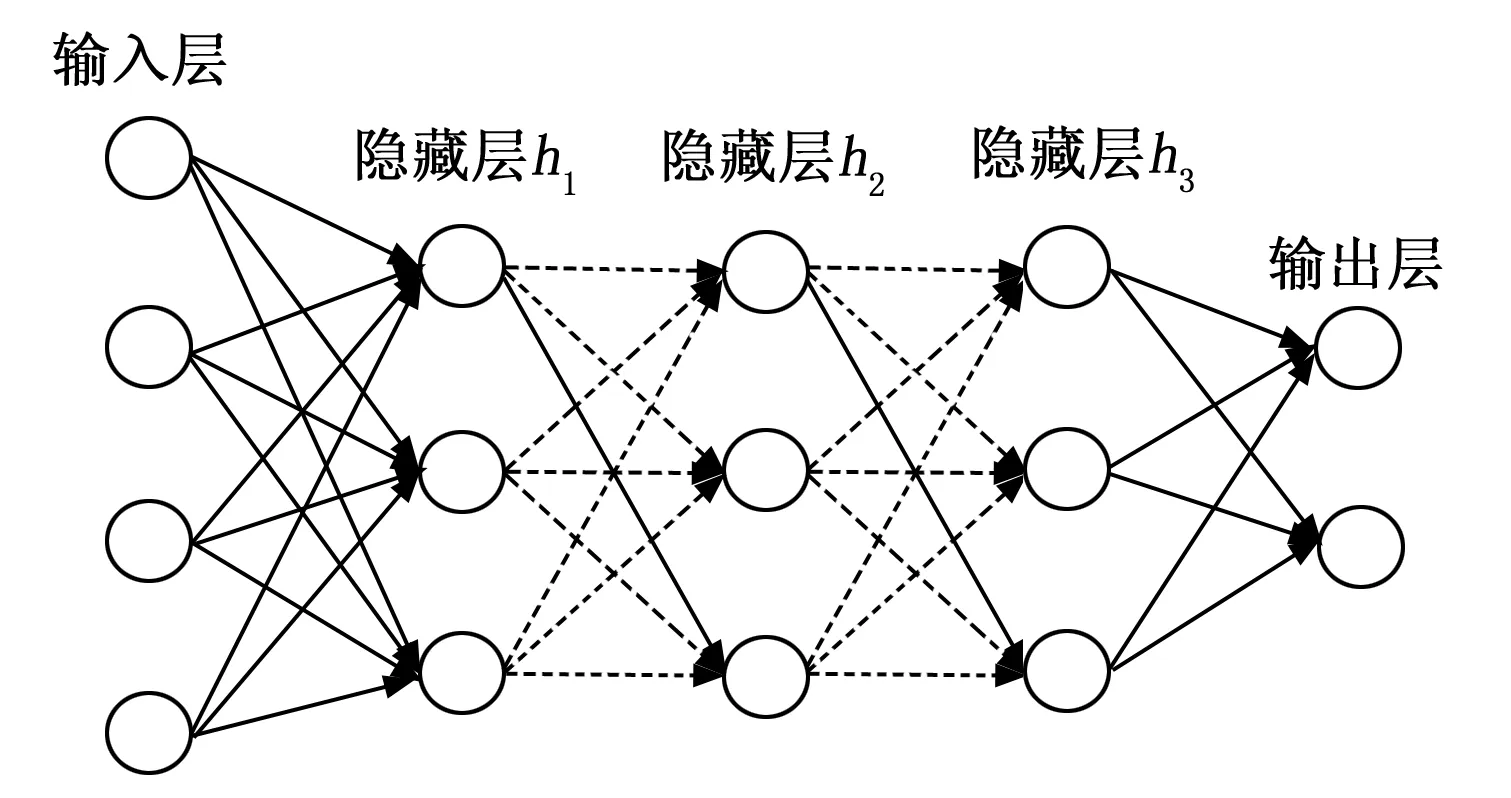
图1 多层前向神经网络
多层前向神经网络,常通过误差反传机制和梯度信息,对神经元的连接权进行迭代优化,这就是流行的误差反传学习算法,简称BP(back propagation)算法,对应的神经网络亦俗称为BP神经网络。BP算法是一种确定性优化算法,收敛速度快,但由于采用单点、惯序的确定性优化模式,不同的初始条件下会收敛到不同的局部极值。采用群智能优化算法训练神经网络时,尽管群智能优化算法具有理论上的全局收敛能力,但由于这类算法属于随机优化算法,早熟收敛现象一直存在。
因此,不论是确定性优化算法,还是随机优化算法,局部收敛或早熟收敛导致神经网络在不同初始条件下,训练结果也不尽相同,训练结果的一致性问题始终存在。
1.1 并联网络结构
为了能保持训练结果的一致性,本文对常规的神经网络进行结构改进,提出了一种由多个神经网络单元组成的并联网络结构。
如图 2所示,神经网络单元NNk(k=1,2,…,K)是由常规的前向神经网络(如图 1所示)组成,所有神经网络单元的输入端并联在一起,各单元的输出相加后形成神经网络的输出。神经网络单元的级联数量,在训练过程中,通过自组织行为自适应确定。
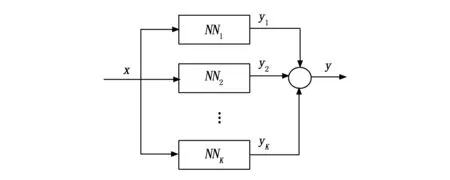
图2 并联神经网络结构
由于神经网络单元NNk的非线性,并联后的神经网络同样具备非线性特征,理论上可以实现对任意非线性函数的高精度逼近。
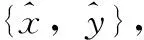
1.2 自组织机制
为了能采用常规的BP算法对图 2所示的并联神经网络进行训练,实现训练结果的一致性要求,对神经网络单元进行功能做如下定义。
定义:后一级神经网络单元NNk+1作为前一级神经网络单元NNk的补偿单元,在神经网络训练过程中,对上一级神经网络单元的训练残差进行补偿。
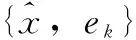
按照上述自组织机制构建的并联神经网络,只要神经网络单元的级联数不受限制,理论上都可以满足训练的精度指标,从而实现训练结果的一致性要求。
例如,设输入样本为:
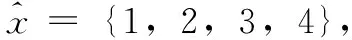
对应的输出样本为:
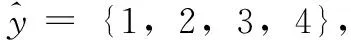
即输入输出训练样本集为:
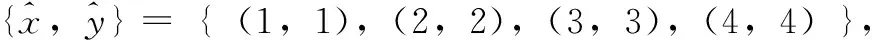
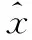
y1={0.9,2.01,3.05,3.95},
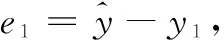
e1={0.1,-0.01,-0.05,0.05}。
利用训练残差e1,构造下一级神经网络单元NN2的训练样本集:
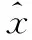
y2={0.11,-0.011,-0.04,0.06},
则神经网络单元NN2的训练残差为e2=e1-y2,即:
e2={-0.01,0.001,-0.01,-0.01}。
这样,神经网络单元NN3的训练样本集为:
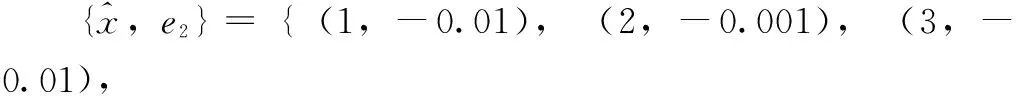
依此类推,只要将输入输出训练样本集作为第一级神经网络单元的训练样本集,其余各级神经网络单元的训练样本集,均可利用上一级的训练残差进行构建,直到训练残差ek满足精度要求为止。
APSNN的样本构建流程及网络结构自适应流程图分别如图 3和图 4所示。
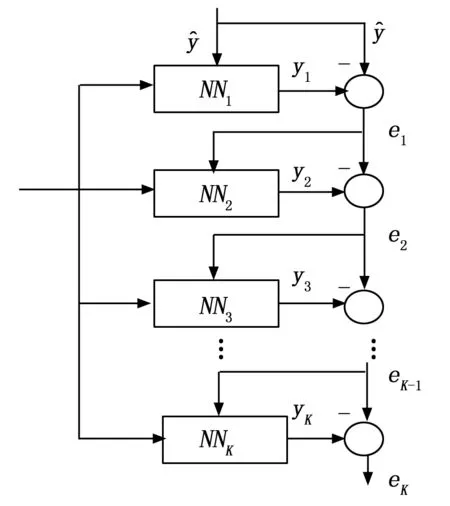
图3 APSNN样本构建流程
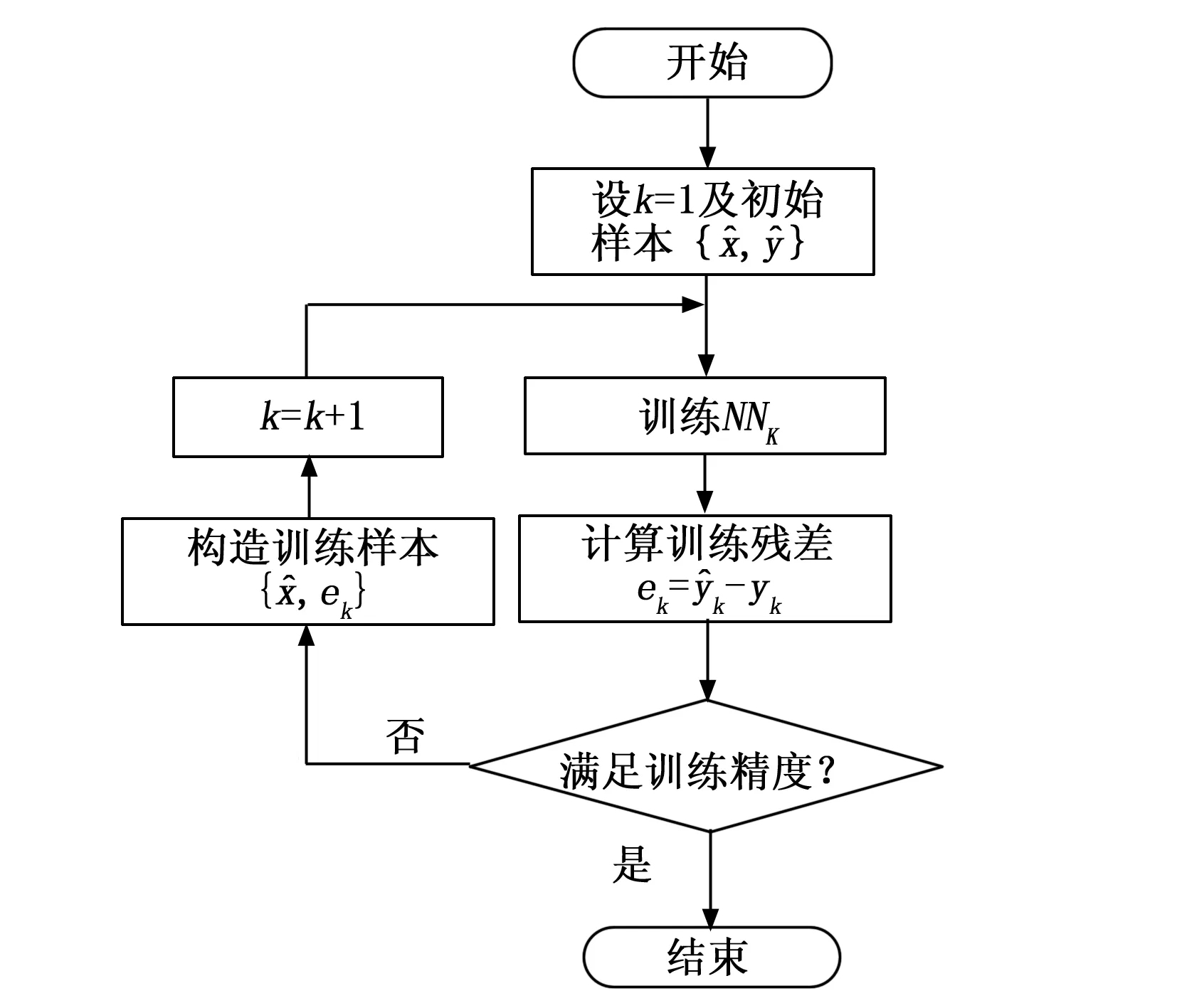
图4 APSNN自组织流程图
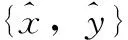
2 函数逼近测试
为了评价神经网络的训练性能,引入三项指标。
第一项指标是式(1)所示的逼近精度,即所有样本均方误差的对数:
(1)
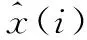
逼近精度的大小能够反映出神经网络的对函数的逼近程度,数值越小,逼近度越高。
第二项指标是式(2)所示的逼近精度的总体标准差:
(2)
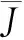
总体标准差反映出数据集在其均值附近的聚集程度。总体标准差越小,说明数据越集中,一致性较好。但考虑到逼近精度JK是训练残差的对数运算结果,因此,逼近精度JK在不同数量级处的总体标准差,难以反映出训练残差的一致性。故总体标准差仅反映逼近精度在数学意义上的一致性。
第三项指标是达标率,即多次独立实验中满足逼近精度的比例。
达标率可以反映出神经网络在逼近精度及其一致性方面的综合性能。达标率越高,说明满足逼近精度的训练次数越多。从工程应用角度看,达标率越高,需要对神经网络重复训练的次数就越少。因此,达标率更能反映出训练残差在工程意义上的一致性。
2.1 函数逼近测试
选取5个非线性函数作为测试函数:
(3)
采用BP神经网络和本文提出的APSNN对上述5个非线性函数进行逼近实验。
实验测试中,设置JK=-4作为达标率的精度阈值,即:当逼近精度小于-4时,认为训练结果达标(当逼近精度小于精度阈值时,能够获得满意的逼近效果)。
为了简化APSNN中的神经网络单元,各神经网络单元具有完全相同中间层数、隐节点数N和激活函数(sigmoid函数)。同时,为了能在相同条件下比较两种神经网络的性能,BP神经网络采用与APSNN完全相同的激活函数。两种神经网络均使用默认的LM算法进行训练,且终止条件也完全相同。
APSNN自组织规则如下:
1)JK=-4;
2)或者并联一级神经网络单元后导致JK增大;
3)或者并联的神经网络单元数达到5个。
当满足上述3个条件中之一时,APSNN自组织结束;当上述3个条件均不满足时,APSNN在原有的结构中,自动并联一级神经网络单元,实现结构扩张。
实验测试在Matlab平台(软件版本2018b)上进行。BP神经网络和APSNN中神经网络单元的训练终止条件均采用相同的默认条件,且在所有实验测试过程中保持不变。APSNN第一个神经网络单元的初始连接权与BP神经网络的初始连接权均为相同的随机数,后续并联的神经网络单元连接权为随机数。
针对函数f1(x),在区间[-6,6]内,按照步长0.01进行采样,形成121个采样点的输入输出训练集。
图 5为BP神经网络不同隐节点的50次独立训练结果。从逼近精度曲线上看,逼近精度的均值随着隐节点数的增加而减小(具体数据见表 1实验结果)。
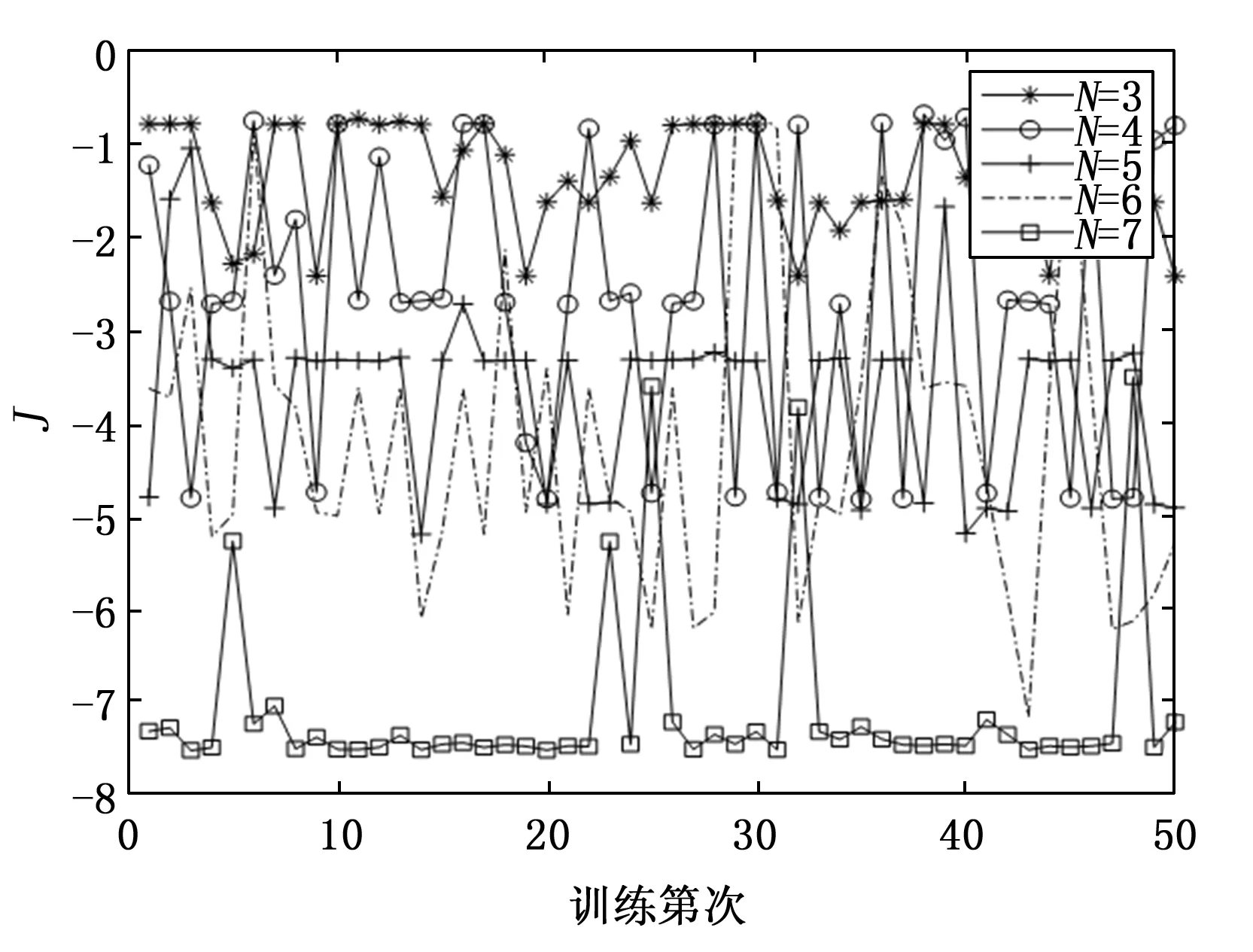
图5 BP神经网络的逼近精度
但是,在50次独立训练中,逼近精度值存在着较大的波动。例如N=3时,近50%的值分布在[-1,0]区间内,40%分布在[-1,-2]区间上,还有10%分布在[-2,-3]区间中。当N=7时,逼近精度的一致性有了明显的改善,数据主要集中在[-7,-8]区间上(共有45次),只有5次实验结果分散在[-3,-6]区间上。因此从数据分布的聚集程度上看,7个隐节点神经网络训练结果的一致性好。
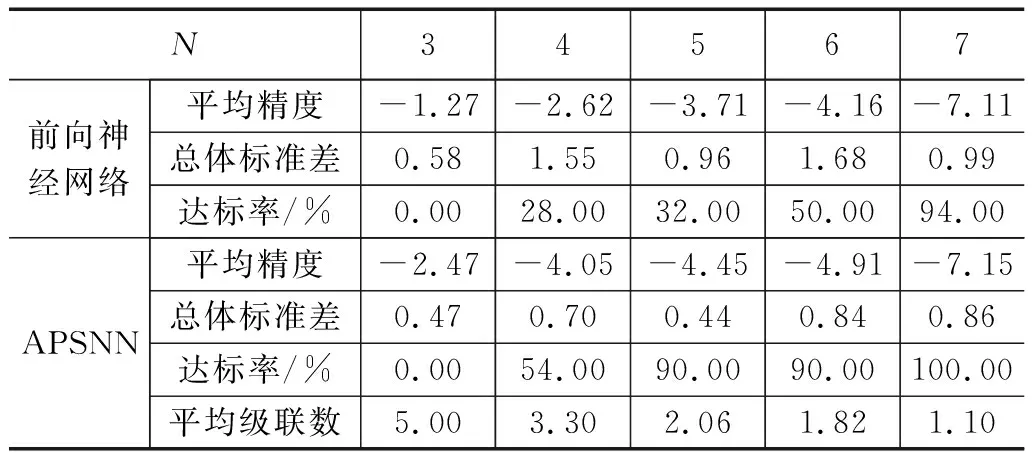
表1 函数f1(x)的实验结果
在表1所示的实验结果中,尽管3个隐节点BP神经网络的总体标准差在数值上要小于7个隐节点BP神经网络,但训练残差的均值处在不同数量级。从数据分布上看,7个隐节点BP神经网络仅有5次实验的数据分布“异常”;另外,从达标率指标上看,7个隐节点BP神经网络有94%的训练结果满足逼近精度指标要求,可以被工程接受。因此,采用达标率来衡量训练结果的一致性更具有工程上的合理性。
图6为APSNN在不同隐节点数(此处指神经网络单元的隐节点数)下50次独立训练结果。当N=3时,逼近精度近75%集中在[-2,-3]之间,明显高于BP神经网络。当神经网络单元的隐节点数N=7时,APSNN与BP神经网络的逼近精度曲线非常相似。APSNN尽管仍有5次逼近精度偏离[-7,-8]区间,但逼近精度均小于-4,而BP神经网络则有3次逼近精度值大于-4。
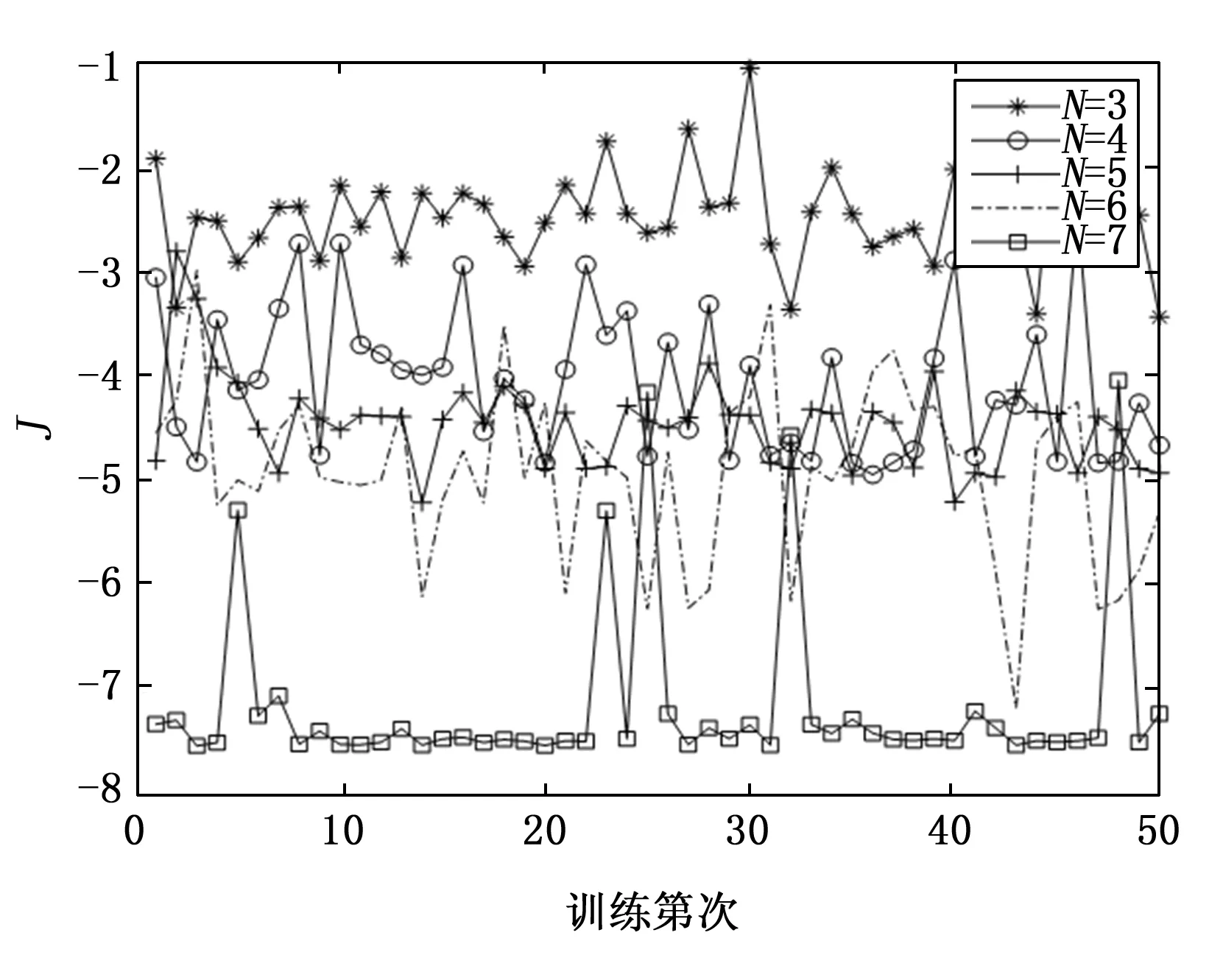
图6 APSNN逼近精度
表1的数据对比表明,APSNN在三项指标方面均优于BP神经网络。这种性能改善,与神经网络单元的残差补偿机制有着密切的关系。
图7是APSNN中神经网络单元级联数在50次独立实验中的变化情况。当神经网络单元的隐节点数为N=3时,由于逼近精度无法满足精度要求,根据自组织规则,在训练过程中会自动并联一级神经网络单元,直至并联数量达到上限5个。随着神经网络单元的隐节点数的增加,神经网络单元的逼近能力得到提升,需要并联的神经网络单元数越来越少。当神经网络单元的隐节点数为N=7时,只出现过两次2个神经网络单元并联的现象,其余48次训练由于达到了精度指标要求,因而只需要一级神经网络单元。此时APSNN差不多就退化为一个常规的BP神经网络,故二者在相同初始条件下,有48次训练结果完全相同。
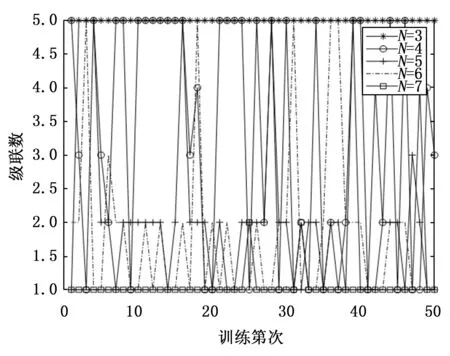
图7 APSNN级联数
表2~表5是BP神经网络和APSNN逼近函数f2(x)~f5(x)的实验结果(实验样本的采样间隔均为0.01)。
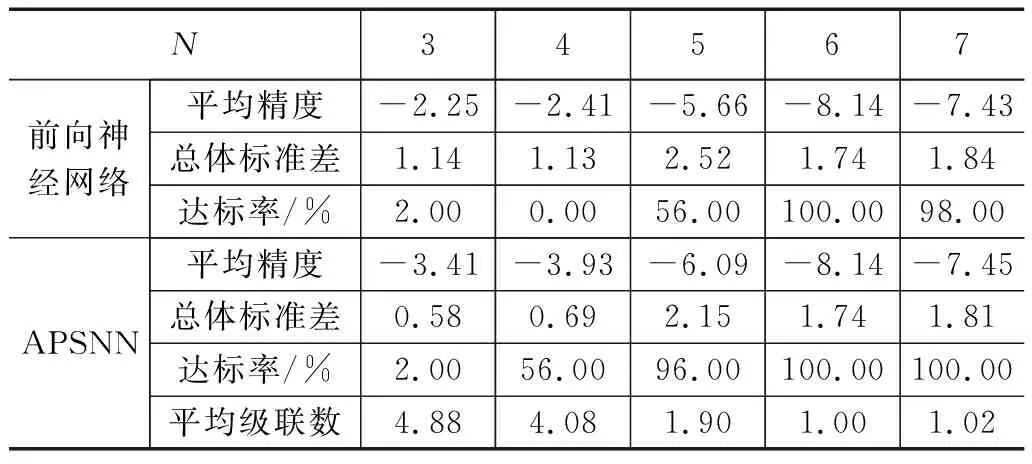
表2 函数f2(x)的实验结果
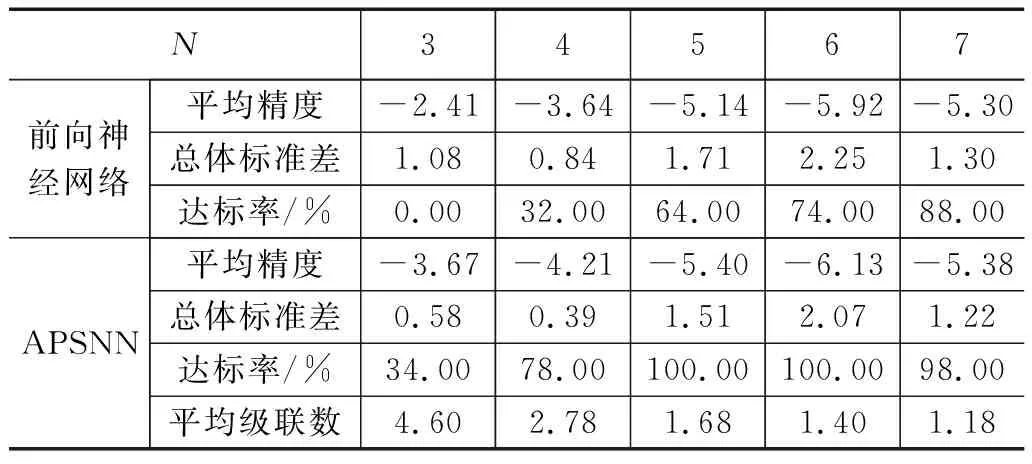
表3 函数f3(x)的实验结果
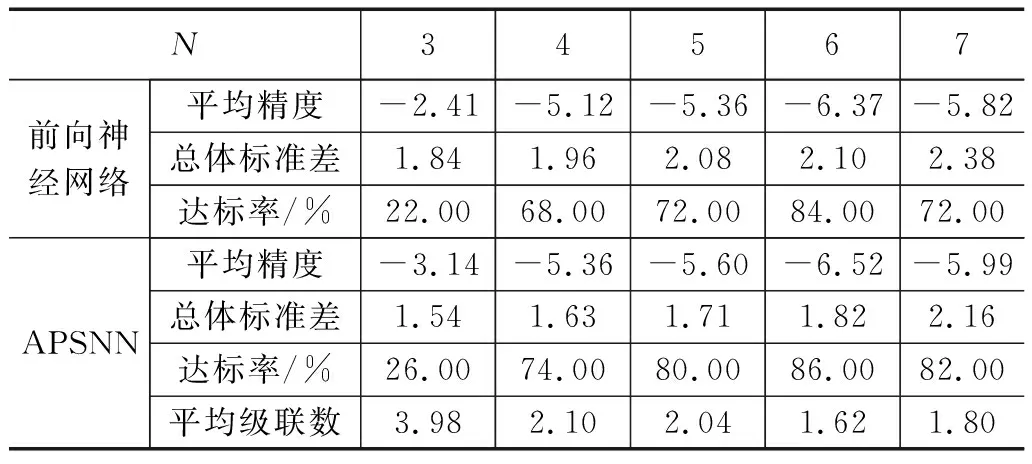
表4 函数f4(x)的实验结果
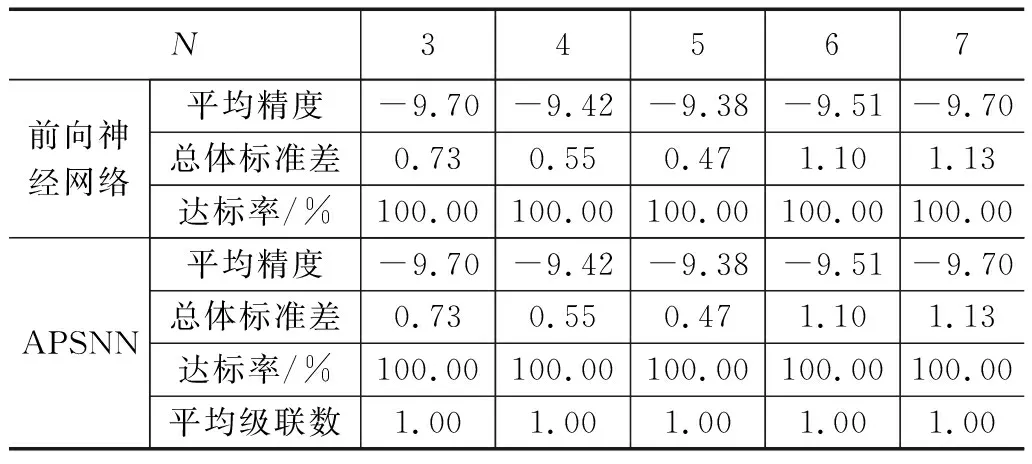
表5 函数f5(x)的实验结果
实验对比结果与函数f1(x)非常相似,APSNN在3项性能指标方面均优于常规的BP神经网络。在函数f5(x)的实验结果中,当APSNN的神经网络单元级联数为1,APSNN就等同于常规的BP神经网络,二者性能完全相同。
在APSNN训练过程中,神经网络根据训练残差的精度要求,通过触发自组织规则,由小到大地搭建神经网络结构,从而实现网络结构的自适应优化。而常规的神经网络结构优化,通常是对神经网络的不同候选结构进行性能评估,从中“挑选”出最优性能指标的网络结构。从二者的不同之处可以看出,常规神经网络结构优化不可避免地对同一结构进行重复评估,而APSNN的自组织规则能同时进行参数和结构优化,避免了神经网络单元的冗余评估,降低了优化过程的计算量。
3 交通流量预测
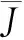
(4)
式中,d(i)为真实流量数据,p(i)为预测模型输出的预测数据。
考虑到交通流量与前一时刻的流量有关,本文采用前4个采样时刻的流量信息预测下一时刻的交通流量,因此,APSNN输入层节点数设为4,输出层节点数为1。当训练精度J≤5或者并联新的神经网络单元导致J增大时,训练过程中的自组织行为停止,训练结束。
选取美国明尼苏达州的明尼阿波利斯和圣保罗之间94号州际公路2018年9月1~30日的西行数据作为测试数据(数据源:https://archive.ics.uci.edu)。前25天的600个监测数据(每小时采集一次交通流量)作为神经网络的训练样本集;利用训练好的神经网络,预测后5天的交通流量。
图8是50次独立测试的预测精度变化曲线。从图中曲线的可以看出,APSNN和BP神经网络的预测精度相近,大部分预测精度在5.2附近,而WNN则在5.5附近波动。但是,APSNN在50次独立测试中的预测精度相差不大,一致性更好,而BP和WNN则出现了较大的波动。
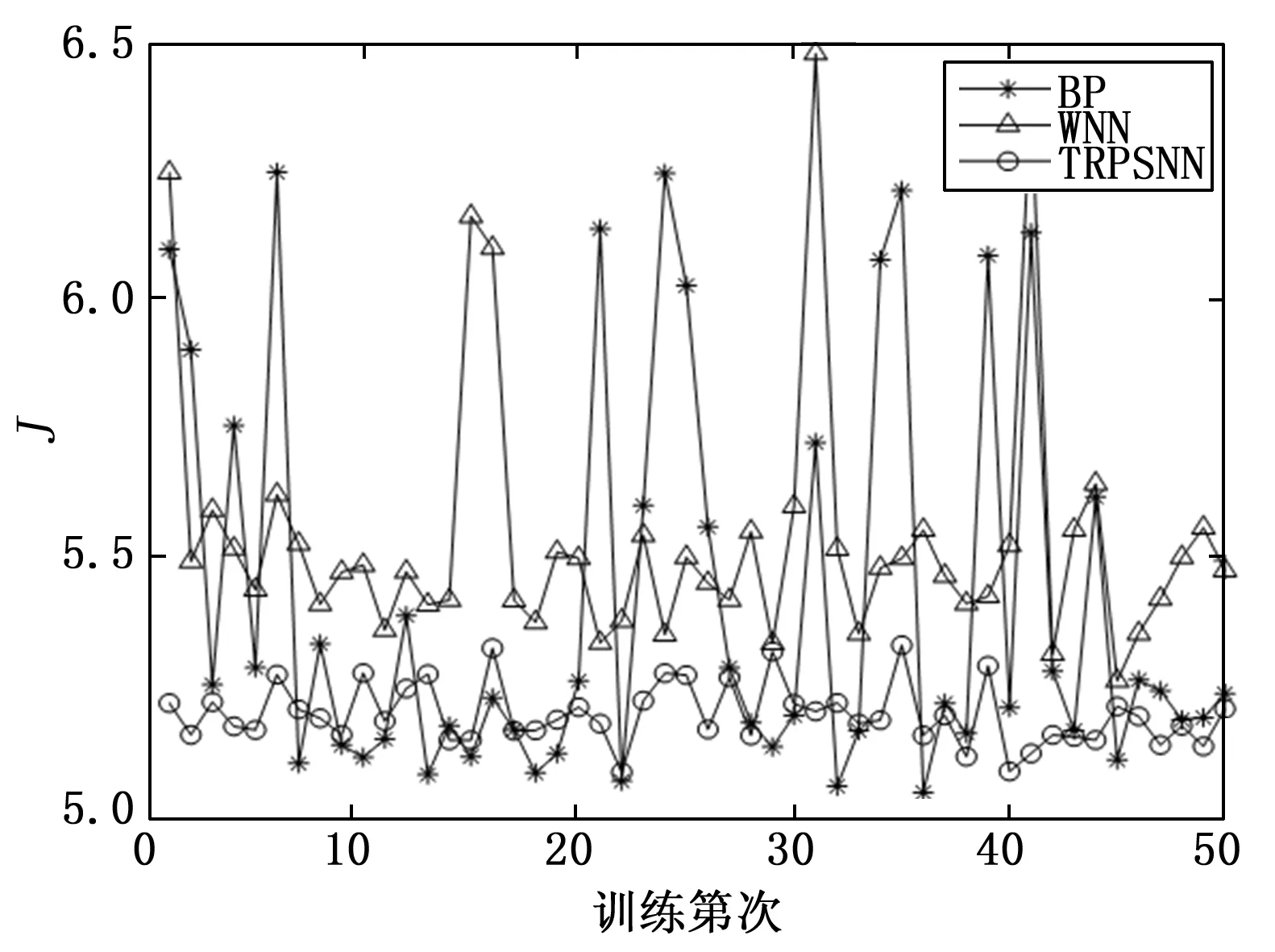
图8 预测精度
为了能更直观地比较预测的一致性,先计算单次实验中120个预测点的总体标准差,作为每个预测时刻的一致性性能指标,然后以这个总体标准差作为数据集,计算50次实验中的总体标准差,作为重复测试的一致性性能指标。
图9是3种神经网络的在50次实验中的总体标准差曲线。APSNN和BP的总体标准差大部分在400~500附近,而WNN在600附近波动。但APSNN在50次独立实验中的总体标准差非常平稳,这意味着APSNN不但在重复测试中表现稳定,而且在每个预测时刻的偏差也比较稳定。而BP次之,WNN最差。
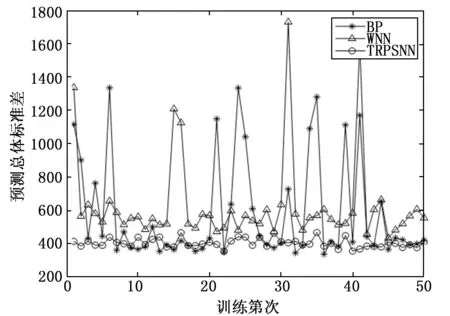
图9 预测标准差
表6是3种神经网络在50次独立测试中的3项性能指标。本文提出的APSNN在3项指标方面均表现优秀。在MAPE指标上,APSNN较BP和WNN分别降低了2.7%和9.7%。因此,采用APSNN进行交通流量预测,既能降低预测偏差,又能保持预测的平稳性。
表6 交通流量预测结果
4 结束语
由于现有优化算法的局限性,神经网络的逼近精度和训练结果的一致性难以保证,给工程应用了带来不便。本文提出了一种自适应并联结构的神经网络——APSNN。这种神经网络可以利用常规的优化算法,对神经网络单元进行逐级训练。在训练过程中,神经网络根据训练残差实现网络结构优化,确保训练精度及其一致性。
APSNN的自组织行为是通过神经网络单元的自适应并联扩展实现,不是对单个神经网络的内部隐含层和隐节点进行增删,这是本文与神经网络传统优化方案不同的地方。由于目前神经网络单元内部结构固定、隐节点数无法自适应,这是APSNN的不足之处。探索神经网络单元的结构优化,将是未来要解决的一个问题。

