抓住图形特征 破解折叠问题
张庆森


摘 要:正方形是初中数学中常见的平面几何图形,与正方形有关的线段长度或图形面积计算问题是历年中考数学的热点问题.文章对2023年扬州市中考数学第18题的解法进行了深入研究,根据图形的基本特征,利用全等三角形的性质、勾股定理、相似三角形的性质等知识给出本题的多种解法,并根据图形特征,给出本题的两个有趣变式.通过“一题多解”学习实践活动,不仅可以培养学生的推理能力,而且可以提升学生的数学核心素养.
关键词:正方形;折叠;勾股定理;相似三角形
正方形是初中数学中常见的平面几何图形,它是最特殊的平行四边形,具有平行四边形的所有性质.与正方形有关的线段长度或图形面积的计算问题倍受命题者的青睐,是历年中考数学的热点问题.本文对2023年扬州市中考数学第18题的解法进行了深入研究,根据图形基本特征,给出了问题的多种解法和两个有趣变式.
1 试题呈现
(2023年扬州市中考数学第18题)如图1,已知正方形ABCD的边长为1,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B′处,如果四边形ABFE与四边形EFCD的面积比为3∶5,那么线段FC的长为 .
2 试题分析
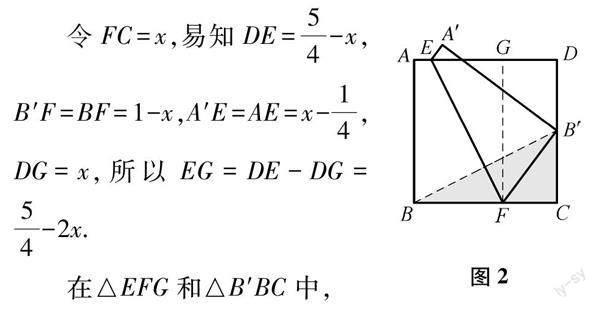
本题是一道以正方形为基本图形,以图形的轴对称为问题情境的线段长度计算题.从已知条件来看,本题需将四边形ABFE与四边形EFCD的面积之比转化为相关线段之间的数量关系.如图1,根据图形特征,易发现四边形ABFE与四边形EFCD都是直角梯形,由梯形的面积公式知S梯形ABFE=1/2(AE+BF)·AB,S梯形EFCD=1/2(FC+DE)·CD,从而可得S梯形ABFE/S梯形EFCD=AE+BF/FC+DE=3/5.又AD=BC=1,所以AE+BF=3/4,FC+DE=5/4.令FC=x,则DE=5/4-x,B′F=BF=1-x,A′E=AE=x-1/4.因此,根据图形特征,构建已知条件与所求结论之间的逻辑关系是解决本题的关键环节,方程是解决本题的重要工具.从图形特征来看,四边形A′B′FE与四边形ABFE关于直线EF对称,∠A′=∠A=90°,∠A′B′F=∠B=90°,由此易得△A′EG∽△CFB′,△B′DG∽△FCB′(G为A′B′与AD的交点).从而可考虑利用勾股定理和相似三角形的性质列方程解决问题.根据正方形的基本特征,也可构造全等三角形解决问题.因此本题主要考查正方形的性质、轴对称图形的性质、直角三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质,其综合性较强,是填空题中的一道压轴题,对学生而言具有一定的难度.
3 解法探究
基于以上分析,本题有多种解法.
思路1 利用勾股定理列方程求解
解法1:如图2,过点F作FG⊥AD,垂足为G,连接BB′.
4 变式探究
变式1:如图1,已知正方形ABCD的边长为1,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B′处,如果四边形ABFE与四边形EFCD的面积比为3∶5.求证:点B′是CD边的中點.
变式2:如图1,已知正方形ABCD的边长为1,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B′处,如果梯形ABFE与梯形EFCD的面积比为3∶5.求BF∶FC的值.
5 结语
从几何图形入手,抓住图形的基本特征,是探寻几何问题中已知条件与所求量之间逻辑关系的关键.在解决与正方形有关的折叠问题时可利用直角三角形或相似三角形构建已知条件与所求结论之间的逻辑关系,然后利用方程思想解决问题.当已知条件与所求结论之间的逻辑关系不明显时,可根据图形特征适当添加辅助线,使已知条件与所求结论之间的逻辑关系外显化,为问题解决创造便利条件.通过“一题多解”学习实践活动,不仅可以培养学生的推理能力,而且可以提升学生的数学核心素养.
参考文献:
[1] 畅英英.初中数学教学中有关折叠问题的解题研究[J].数理化解题研究,2021(29):2829.
[2] 焦鸥.新课程下基于初中数学折叠问题的教学思考[J].数学学习与研究,2020(28):121122.

