直线、平面垂直的判断及性质中的数学素养
■石汉荣 刘大鸣(特级教师)
以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理,运用公理、定理和已获得的结论证明一些有关空间图形的垂直关系,凸显逻辑推理、直观想象、数学运算的核心素养。
一、与线、面垂直相关命题的判断
例1下列命题中错误的是( )。
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
解析
对于A,设平面α∩β=a,设b⊂α,且b//a,显然直线b⊄β,根据线面平行的判定定理得b//β,A 正确。对于B,如果α内存在直线与β垂直,则由面面垂直的判定定理知平面α⊥β,这与已知矛盾,B 正确。对于C,设平面α∩γ=a,平面β∩γ=b,在平面γ内作直线m⊥a,n⊥b,由面面垂直的性质定理得m⊥α,n⊥β,由直线l⊂α,l⊂β,可得m⊥l,n⊥l,由α∩β=l,可得m,n为相交直线,所以l⊥平面γ,C 正确。对于D,平面α⊥β,设平面α∩β=a,在平面α内与a平行的直线都不与平面β垂直,D 错误。应选D。
素养:与线、面垂直的相关命题的真假判断问题,正确的需说明原因,不成立举出反例即可。线线、线面、面面垂直的五个常用结论:若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线;若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面;垂直于同一条直线的两个平面平行;一条直线垂直于两平行平面中的一个,则这条直线与另一个平面也垂直;两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面。
二、直线与平面垂直的判断与性质
例2如图1,已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为3,那么点P到平面ABC的距离为_____。
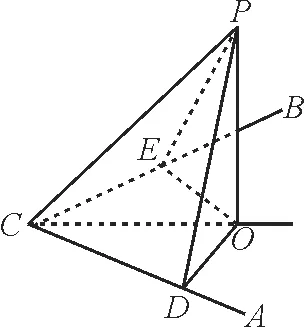
图1
解析
过点P作PD,PE分别垂直于AC,BC于D,E,作PO⊥平面ABC于O。
因为PO⊥平面ABC,所以PO⊥AC,所以AC⊥平面POD,所以AC⊥OD。同理,BC⊥OE。所以四边形CDOE是矩形。
素养:证明直线和平面垂直的四种常用方法:判定定理;平行线的传递性(a//b,a⊥α⇒b⊥α);面面平行的性质(a⊥α,α//β⇒a⊥β);面面垂直的性质。证明线面垂直的关键是证明线线垂直,而证明线线垂直则需借助线面垂直的性质。
三、平面与平面垂直的判断与性质
例3如图2,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点。过B1C1和点P的平面交AB于E,交AC于F。
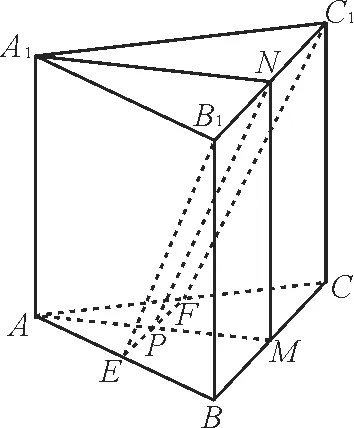
图2
证明:AA1//MN,且平面A1AMN⊥平面EB1C1F。
证明:因为M,N分别为BC,B1C1的中点,所 以MN//BB1。又AA1//BB1,所 以MN//AA1。
在等边△ABC中,M为BC中点,则BC⊥AM。因为侧面BB1C1C为矩形,所以BC⊥BB1。因 为MN//BB1,所 以MN⊥BC。由MN∩AM=M,MN,AM⊂平面A1AMN,可得BC⊥平面A1AMN。
因为B1C1//BC,且B1C1⊄平面ABC,BC⊂平面ABC,所以B1C1//平面ABC。因为B1C1⊂平面EB1C1F,且平面EB1C1F∩平面ABC=EF,所以B1C1//EF,所以EF//BC。又因为BC⊥平面A1AMN,所以EF⊥平面A1AMN。
因为EF⊂平面EB1C1F,所以平面EB1C1F⊥平面A1AMN。
素养:在垂直关系的证明中,线线垂直是证明的核心,可以根据已知的平面图形通过计算的方式(如勾股定理)证明线线垂直,也可以根据已知的垂直关系证明线线垂直。判断面面垂直的两种方法:面面垂直的定义;面面垂直的判定定理(a⊥β,a⊂α⇒α⊥β)。
感悟与提高
若点P是两条异面直线l,m外的任一点,则( )。
A.过点P有且仅有一条直线与l,m都平行
B.过点P有且仅有一条直线与l,m都垂直
C.过点P有且仅有一条直线与l,m都相交
D.过点P有且仅有一条直线与l,m都异面
提示:过点P与l,m都平行的直线不存在;过点P与l,m都垂直的直线只有一条;过点P与l,m都相交的直线最多有一条;过点P与l,m都异面的直线有无数条。应选B。

