基于集分割模型的复杂机场地勤人员排班研究

黄梦婷　缪彬

摘要：为了优化机场地勤人员的调配管理，提升机场服务质量，文章对传统的排班模式进行研究并改进，结合我国机场运营实况，借鉴国内外排班优化模型的理论与研究成果，建立以最小化班期成本为目标的集合分割排班模型，以最小化各项任务成本为目标，采用列生成算法对模型进行求解。该研究成果能够有效优化机场地勤人员的调配，在一定程度上提升机场服务质量，同时能快速解决机场地勤人员排班问题，对进一步推进人员排班模型及算法的研究有着积极作用。

关键词：地勤人员排班；集合分割模型；列生成算法；组合优化

一、引言

机场逐年增加的吞吐量会造成对地勤人员需求的增加，同时对其排班的难度也大幅增加，具体原因如下：不同任务类型需要不同的人员资质；多种工种，不同工种具有不同的排班规则；地勤排班计划对算法的鲁棒性和时间需求较高。因此，机场地勤人员排班本质上是，综合考虑航班到达不确定性、多任务、多工种情况下的复杂排班问题。

人员排班的主要研究内容是通过定义要完成的任务，及其开始时间段、工作持续时间、休息时间间隔等，为每个员工构建工作时间表以满足各种地勤服务需求，被广泛应用于医疗保健领域、交通运输、呼叫中心等领域。参考机组排班计划问题将地勤人员排班问题划分为人员派工和人员指派两个子问题。派工是地勤人员排班计划的主要任务，是将机场保障服务按要求匹配成一串没有时间冲突的任务序列，人员指派则是在人员派工的基础上，指派具体的不同资质的员工完成具体的保障任务。本文则具体研究作为排班计划核心阶段的人员派工问题。

目前，围绕地勤人员排班计划生成的研究有：Soukour等为降低地勤服务调度模型的复杂性，将其分为三个步骤求解：休息日安排、轮班安排和员工分配；Ip等将地面服务的调度优化问题描述为具有多个不同车辆的时间窗的车辆路径问题，为了解决这个问题，提出了一种混合编码的遗传算法；Clausen研究了多任务、面向层次资质需求的地勤人员排班问题，并使用模拟退火算法对模型进行求解。国内关于地勤服务调度问题的研究大多集中于车辆调度优化以及航班进出港排序优化问题上；卢敏、冯霞等分别研究了面向班型动态生成和面向层次资质的机场地服人员排班问题，克服了传统人员排班模型中的单一任务、单一资质问题。

上述研究成果一般集中于对地勤服务流程和模型约束条件的改进，且这些研究中大部分是针对单一的或特定类别的地勤服务进行调度，很少考虑从全局角度为机场地勤人员建立模型进行统一排班调度。为解决该问题，本文建立集合分割排班模型，以最小化各项任务成本为目标，采用生成算法对模型进行求解，为每一个班期生成可行的任务序列，建立更加全面的机场地勤人员协同排班模型。

二、问题模型构建

（一）问题描述

1. 模型相关概念

班期组：根据机场地勤保障的要求，按时间窗划分所需的不同班期类型，班期规定了地勤服务人员的到岗时间和离岗时间。班期组是指同一时间窗内的多个同类型班期的集合。

任务序列：就是指一串没有时间冲突的任务串，排班派工阶段的任务就是要找到适配于每个班期的最优的任务序列。

2. 模型的基本假设

相关成本假设：模型目标函数为班期成本最小化。模型的成本主要包括：任务不被覆盖的惩罚成本；班期的设置成本以及任务津贴。任务津贴具体包括员工执行任务的固定成本以及人员资质成本。

航班为周期性重复假设：模型假设航空公司的航班计划是周期性重复的。面对周期性的航班计划，机场地勤服务部门能以一定的周期为单位对地勤人员进行编排。

（二）模型构建

本文将地勤人员排班问题刻画为集合覆盖问题，建立如下模型：

式中：r表示任务序列，r∈R，R为全部可行任务序列集合；t表示任务，t∈T，T为所有待执行任务集合；s表示班期，s∈S，S为所有可能的班期类型；当r∈Rt时，xr的0-1取值表示r任务序列中是否包含t任务；当r∈Rs时，xr的0-1取值表示s班期中是否包含任务序列r，yt的0-1取值表示任务t是否没有被覆盖；zt表示任务t是否被多次覆盖；cr表示任务序列r的成本（含人力成本、物资成本）；c■■表示取消任务t的惩罚成本；c■■表示任务t被多次覆盖的惩罚成本。

式（1）为主问题模型的优化目标，任务执行的总成本最小；式（2）为任务覆盖约束，要求所有任务t∈T都被覆盖且仅被覆盖一次；式（3）为班期数量约束，要求每个班期组内的班期数量，要大于该班期时间段内可执行的任务序列个数；式（4）表示xr为0～1变量，表示第r个任务序列是否被选择；式（5）表示yt为0～1变量，表示任务t是否没有被覆盖；式（6）表示zt为0～1变量，表示任务t是否被多次覆盖。

三、基于列生成的模型求解算法

（一）算法的基本思想

列生成算法求解思路源于单纯形法，区别在于，列生成算法不需要计算验证原问题的所有的检验数，是以隐枚举方式为原问题提供较优“基变量”。基于本文，是将原问题分解为一个寻找最优派工方案组合的主问题和一个寻找新任务序列的子问题。主问题中的只包含部分可行任务序列，为受限的集合分割问题，对主问题进行松弛后求解，将得到的对偶解传递给子问题；带有成本约束的最短路子问题模型利用主问题的对偶信息寻找新的任务序列并加入主问题模型，通过这样的循环迭代，主问题不断增加新变量，其求解结果逐渐逼近原问题的最优解，当模型系统满足一定收敛准则时即完成模型的求解。具体算法流程如图1所示。

（二）受限主问题模型

本文将所有单个任务作为主问题的初始可行变量，即一个任务就代表一個任务序列。受限主问题表示如下：

其中，R1表示部分初始可行任务序列的集合，R1＜<R，R■<<Rt，R■<<Rs。

（三）子问题模型构建

由于对任务序列的时间跨度约束主要体现在“班期组s的任务序列集合Rs”上，即除了为每个班期组生成任务序列集合，还要求集合中每个任务序列是可以在该班期组工作时间窗内被执行的任务序列。在派工阶段，每一个班期组对应一个子问题，通过求解多个子问题模型，为每个班期组寻找更好的任务序列，作为新的列，加入限制主问题。因此在子问题模型中选取任务序列不再需要对任务执行时间的约束进行考虑。

子问题模型的目标是向主问题提供可行的任务序列，可行任务序列的定义是：加入主问题的可行的任务序列必须是差额成本大于零，否则停止迭代，具体子问题模型如下：

）

式中：αi表示i任务的机会成本（即任务覆盖约束对应的对偶变量）；ci表示i任务的执行成本；πs表示s班期的机会成本（即班期数量约束对应的对偶变量）；b（i）表示i任务的前可连接任务集合；a（i）表示i任务的后可连接任务集合；sis表示班期s是否从i任务开始；eis表示班期s是否以i任务结束；xijs表示s班期中的任务i是否与任务j相连；gi表示任务i的执行时间；maxs表示班期的最长时限。

式（13）表示子问题的目标函数，为主问题寻找新的任务序列；式（14）表示流量平衡约束；式（15）表示任务序列只能有一个任务起点；式（16）表示任务序列只能有一个任务终点；式（17）表示地勤人员的任务执行时间小于规定的班期时间段；式（18）表示xijt，xjit，sit，eit为0～1变量。

（四）求解算法

模型的求解大概思路及步骤。

Step1：建立集合分割模型，对数据进行初始化，运用启发式算法获得尽可能高质量的初始集合（可行任务序列）。

Step2：求解松弛的集合分割模型，并求对偶解。

Step3：利用主问题求得的对偶解对子问题进行求解，若子问题中的差额成本小于零则停止生成任务序列，否则继续执行第四步。

Step4：将新生成的任务序列传递给集合分割主问题，增加主问题的列数即增加主问题的任务序列，转到Step2。

Step5：恢复主问题的整数约束并对其求解，获取最后的排班方案。

（五）启发式算法求解初始集合

因地勤人员排班只是对一天的任务进行排列，且任务是根据航空公司的航班飞行计划安排的，各个任务的大概开始和结束时间是已知的，因此其算法步骤较为简单。

首先，根据所有输入的任务可生成一天三个时间段的班期：s1：4：00～12：30、s2：12：00～20：00、s3：19：30～02：30。

Step1：对所有任务按时间划分，分别寻找早中晚班的所有任务对其划分。

Step2：将早、中、晚班中时间没有冲突的任务进行组合。

由于不同任务可能要求不同资质人员执行，人员若不能满足多种资质要求的任务序列，则该任务序列为不可行任务序列，否则就将其列为初始的可行任务序列，转第三步。

Step3：写出初始可行班期组任务序列。由于前面已经对时间进行划分则各班期对应的班期组任务序列集合可相应得到。

Step4：求得各个任务对应的任务序列。

四、实验及分析

（一）实验数据

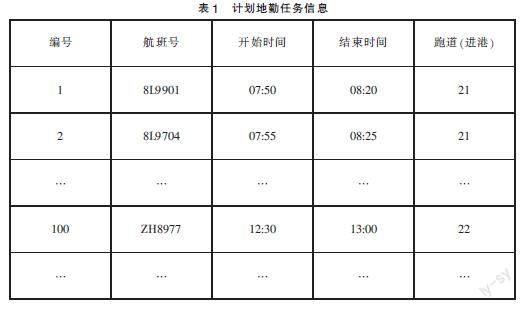
数据选用A机场地勤服务部2020年11月01日一整天的航班到达计划数据，共452个任务信息，包括任务的类型（航班号）、任务开始时间、任务结束时间、航班降落跑道，如表1所示；模型的生成以及模型求解的算法均采用SQL SERVER編写，试验的硬件环境是Intel（R）Core（TM）i5-10210u，2.11GHz主频，16G 内存，Windows操作系统的计算机，使用LINGO 18.0软件对模型进行求解，最后借助EXCEL工具对LINGO的求解结果进行筛选整理。

（二）实验结果

算法的参数设置如下：

成本设置：将测试模型的班期设置成本设为8500元/班；而任务不被覆盖的惩罚成本则假设为10000元/项；任务重复覆盖的惩罚成本为9000元/项。

任务衔接条件设置：所有任务的执行时长统一定为30分钟，同一跑道区域的所属任务，两两时间间隔≥30分钟的任务可相互衔接；不同跑道区域的所属任务，不可相互衔接。

从班期所保障的任务序列角度展示排班结果，表2中的行代表一个班期，规定了班期开始时间、班期结束时间以及保障的任务（航班号）。例如表2中的第1个班期数据表示：第1个班期实际开始时间为07：55，实际结束时间为12：10（属于类班期—早班），该班期保障的任务序列为：任务2、任务13、任务16、任务32、任务44和任务79。

五、结语

本文以机场航班过站期间的地勤服务问题为例，以运营成本最小化为目标，建立了集分割排班模型，由于地勤人员排班问题是典型的NP难问题，要穷尽所有可行的任务序列是几乎不可能的，故实现模型的求解非常困难，于是提出了列生成算法来求解该排班模型。利用A机场的实际数据进行实验，结果表明，相较于传统的排班模型，集分割排班模型能够有效减少模型变量个数，在更短的时间内得到员工班期方案，并且模型求解得到的班期方案能够有效优化机场地勤人员的调配，提升机场服务质量。

参考文献：

[1]Griffiths P，Saville C，Ball J，et al. Nursing workload，nurse staffing methodologies and tools：A systematic scoping review and discussion[J].International journal of nursing studies，2020，103：103487.

[2]Santosa B，Krisnawati M，Rusdiansyah A.Solving crew rostering using metaheuristics，a case study in Indonesia[J].International Journal of Metaheuristics，2020，7（04）：307-329.

[3]蓝伯雄，张米.考虑延误因素的机组排班模型研究[J].中国管理科学，2015，23（12）：167-176.

[4]王秀利，徐悦，胡修武.中小呼叫中心月度排班优化模型与算法[J].中国管理科学，2021，29（04）：169-178.

[5]Soukour A A，Devendeville L，Lucet C，et al.A memetic algorithm for staff scheduling problem in airport security service[J].Expert Systems with Applications，2013，40（18）：7504-7512.

[6]Ip W H，Wang D，Cho V.Aircraft ground service scheduling problems and their genetic algorithm with hybrid assignment and sequence encoding scheme[J]. IEEE Systems Journal，2012，7（04）：649-657.

[7]Clausen T.A Rule-Based Local Search Algorithm for General Shift Design Problems in Airport Ground Handling[J]. transporta，2010.

[8]樊瑋，吴建波，衡红军.基于多 Agent 的机场地面服务车辆调度方法研究[J].计算机应用与软件，2015，32（10）：256-259.

[9]张建同，杨文娟.基于优先级的进离港航班排序优化问题研究[J].运筹与管理，2018，27（06）：115-121.

[10]卢敏，王莉.面向班型动态生成的地服人员排班算法[J].交通运输系统工程与信息，2018，18（04）：54-60.

[11]冯霞，唐菱，卢敏.面向层次资质的机场外航服务人员排班研究[J].交通运输系统工程与信息，2018，19（02）：231-237.

[12]Van Hoai T，Reinelt G，Bock H G.Advanced column generation techniques for crew pairing problems[M]//Modeling， Simulation and Optimization of Complex Processes.Springer，Berlin，Heidelberg，2005：203-214.

＊基金项目：云南省教育厅省院省校合作项目“边疆欠发达地区中小企业创新发展对策研究”（课题编号KKDA202008001）。

（作者单位：昆明理工大学管理与经济学院。缪彬为通信作者）