指定流量分配系数的多回流出口边界算法

许开龙，刘再刚，姜胜利，王星，张磐

1．中物院高性能数值模拟软件中心，北京 100088

2．北京应用物理与计算数学研究所，北京 100088

在航空发动机燃烧室数值模拟中，计算域存在燃气和冷却气等多个出口边界，其出口流量分配关系通常根据工程设计要求或实验获得，模拟中需要引入特殊的边界处理方法以获得边界物理量分布作为定解条件，为边界处理方法带来较大挑战。此外，燃烧室中火焰筒等局部的燃烧组织是数值模拟的关注重点之一，截取燃烧室的部分结构作为计算域可显著降低数值模拟的计算量，但常规出口边界条件算法因出口存在回流或未充分发展无法保证计算稳定性和精度。因此，研发可指定流量分配系数、允许出口回流的出口边界算法对提升发动机燃烧室数值模拟软件的工程适用性和仿真置信度有重要意义。

出口边界的处理方式对数值模拟的稳定性和计算准确性有显著影响，是不可压缩流体数值模拟中的一个挑战性问题［1-2］。经过数十年的发展，已有诸多不可压缩流动模拟中出口边界处理方 法 的 研 究。Sani 和Gresho［3］综 述 了 经 典 的 出口边界处理方法，其中基于物理量局部单向化假设的对流边界条件［4］及零法向梯度的充分发展边界条件应用较为广泛［5-6］，但该方法在边界上存在涡团或回流时，会出现数值不稳定现象甚至直接发散，且降低时间步长或增加网格密度并不能改善这种数值不稳定性［7］。在实际应用中，常将出口边界面置于主流区下游足够远处，使得流动产生的涡团在到达出口边界前充分耗散。但主流区涡团的发展和流动雷诺数相关，计算域需要随着雷诺数的增加而扩展，造成了很大的计算资源开 销，如Steggel 和Rockliff［8］采 用 充 分 发 展 边 界条件计算二维圆柱扰流问题，出口边界位于下游125 倍圆柱直径处，主流区仅占计算域一小部分。此外，在海洋环流、大气流动、血液流动等问题中并不存在明确的出口，必须将计算域截断。

针对出口流动未充分发展的情况，Papanastasiou 等［9］首次在有限元离散下提出了自由边界条件，该方法将控制方程的离散拓展到边界上，并将边界上物理量和计算域内的值关联，无需用户额外提供流场信息。何吉欢［10］在有限元框架下进一步讨论了自由边界条件对复杂流场的处理 能 力。Li 和Tao［11］提 出 了 法 向 速 度 满 足 局 部单元质量守恒、切向速度满足齐次Neumann 条件的边界处理方法，并根据全局质量守恒进一步修正法向速度大小，成功实现出口边界上存在回流时传热问题的正确模拟；该方法简单实用，仅需修改速度边界条件而无需调整求解流程。Hasan等［1］通过改进边界上速度插值方法，实现了计算域缩减至6～8 倍特征尺寸时钝体绕流问题的正确计算。Xue 和Barton［12］提出了利用质量流量处理进/出口边界条件的方法，将出口边界处理方法拓展到了多出口的情形，并在二维T 形分叉管算例中验证了计算域大幅缩减、出口边界上存在回流情况时该方法的表现；该方法的优点是，以实际工程中可测量的出口质量流量作为边界条件输入信息，适用于多出口边界情形，提高了工程适用性，但该方法需要修正质量通量的计算方法，对整体的求解流程有一定影响。

不可压缩流体数值模拟中的多出口边界和自由回流出口边界的处理是充满挑战的问题，已有研究发展了适用于不同离散格式的方法，并取得了一定的应用效果，但面向复杂流动［13］、多相流［14］、多开口边界［12］等特征的方法仍在不断发展中。本文拟基于工程中可测量的流量分配系数确定各出口质量流率，发展了可指定出口流量分配系数、出口存在回流的出口边界条件算法，并集成在自主研发的高性能计算流体数值模拟软件中，验证了该出口边界条件的适用性和精度。

1 控制方程和数值方法

1.1 控制方程组及其离散方法

本文求解的不可压缩Navier-Stokes（N-S）方程形式为

式中：ρ为流体密度；u为速度；p为压力；Fl为第l个体积力；μ为流体动力黏度。

采用非结构网格有限体积法对式（1）和式（2）进行空间离散，速度和压力的离散使用基于单元的同位网格和Rhie-Chow 插值。整个计算域被划分为互不重复的微元控制体，取其中一个微元控制体Ω，包围该控制体的内部面元集合为I(Ω)，边界面元集合为B(Ω)，面元面积矢量为S，如图1 所示。使用高斯定理将控制体上散度积分转为通量的表面积分，可以得到积分形式的控制方程为

图1 计算域边界单元示意图Fig.1 Schematic of computational domain boundary cell

式中：下标“i”表示内部面元索引号；下标“b”表示边界面元索引号；=ρiui·Si和=ρbub·Sb分别为内部面元和边界面元上的流体质量通量，ρi、ui、Si和ρb、ub、Sb分别为内部面元和边界面元上的密度、速度和面积；|Ω|为微元控制体体积。针对离散后的N-S 方程，采用SIMPLEC 算法实现半隐式速度-压力的耦合计算，采用二阶Crank-Nicolson 格式离散时间项，采用二阶线性迎风格式计算对流通量，采用中心差分格式计算扩散通量。

1.2 出口边界条件

式（3）和 式（4）中、、-(μ∇u)b·Sb分别表示边界面元b∈B(Ω)上质量通量、动量对流通量和动量扩散通量，是边界条件处理关注的重点。在本文中，压力的出口边界条件设置为Dirichlet 边界条件，而速度u边界条件是研究的主要内容。针对图1 所示控制体，可以采用以下线性关系式描述任意边界面元上的速度和其邻接单元上速度的关系：

式中：uF为边界面元中心F点的速度；quF为单位面积法向通量。为处理网格畸变严重的情形，需要用式（7）将单元中心P点的值重构到P'得到uP'再进行计算。边界条件处理就是确定各面元上的值。

在常规边界处理中，边界上物理量的值可根据实验测量、物理观察等得到，如速度入口边界、壁面边界、对称边界等，进而确定4 个边界系数的值。但对于出流边界上，尤其是未达到充分发展的情况下，边界上物理量的值是未知的，且很难通过实验测量获得边界上的值或者通量分布。

以图1 中F点所在边界面元上边界处理为例，将边界面元速度分解到局部坐标系（n，τ，η）下，如式（8）所示。假设该出口边界上所有边界面元切向速度分量沿法向的梯度为0，而法向速度分量沿法向的变化率为一个常数，记为R，可以得到边界面元上3 个速度分量的计算式为

该方法中实际是将常规速度Neumann 型边界条件变为了Robin 型边界条件。

法向速度变化率R的确定方法需要重点关注。与Li 和Tao［11］的思路类似，本文基于全局质量守恒确定不可压缩流动问题中的出口边界条件。在多出口条件下，引入出口质量流量分配系数αj进行处理：假设计算域有J个出口边界，计算域所有入口边界质量流量及计算域内新增质量（质量源空间积分）之和为Mtot，各出口边界流量分配系数为αj（j=1， 2，…J；ΣJj=1αj=1.0），在不可压缩流体模拟中，全局质量守恒是保证求解稳定的必要条件［12］，可以得到出口目标质量流量Mj为

根据各出口面目标质量约束，结合式（9）、式（12）可以得到第j个出口边界上法向速度变化系数Rj为

结合式（9）～式（11）、式（13），可以得到边界法向速度、切向速度的迭代更新方法为

式中：k表示当前迭代步。

上述出口边界速度值的构造方法实际上与Papanastasiou 等［9］、Li和Tao［11］实现的自由边界条件的思想是一致的，即虽然出口边界面元上速度量是未知的，但当前时间步边界单元的速度场是严格按照N-S 方程的求解得到的，是符合物理规律的、自然的。基于该边界单元速度场构造边界速度值，并以出口面质量流量偏差作为边界速度的修正依据，也是合理的。相比于Xue 和Barton［12］提出的方法，该方法可按照常规的速度边界条件进行实现，无需改动N-S 方程求解流程，易于实现。在充分发展情况下，整体质量守恒已经满足，对应于Rj=0 的情形，结果是完全一致的。在应用实践中发现，上述速度边界条件计算方法在出口面上存在回流且网格畸变较为严重时，可能出现数值不稳定现象，基于P'点法向速度方向修正F点速度方向可以有效改善该不稳定性，修正方法为

式中：sgn(x)为符号函数，x＞ 0 时取值为1，否则为-1。

1.3 算法集成

考虑到实际工程问题构型复杂、计算规模大的特点，本文作者依托中物院高性能数值模拟软件中心自主研制的非结构网格并行编程框架JAUMIN［15］研制了不可压N-S 方程的SIMPLE，SIMPLEC 和PISO 求解算法，隐式欧拉和Crank-Nicolson 时间离散格式，一阶迎风、二阶线性迎风和中心差分空间离散格式，研制形成了面向工程实用和物理模型高效集成的高性能计算流体数值模拟软件。该软件基于非结构网格求解三维、不可压近似、稳态/非稳态形式的N-S 方程，支持常见类型的三维凸多面体网格，集成了工程常用的雷诺时均类湍流模型、大涡模拟类湍流模型、传热模型、输运方程求解功能、时空离散格式以及进口、出口、壁面、对称边界等典型物理边界条件。目前，该软件已成功应用于复杂结构湍流、航空发动机两相湍流燃烧、流-固耦合传热等问题的数值模拟，并基于广州“天河二号”超级计算机实现万核、1.6 亿四面体-六面体混合网格的流动模拟，并行计算效率超过70%，表现出良好的大规模并行扩展能力。

本文将发展的出口边界处理算法集成到自主研制的高性能计算流体模拟软件中，基于典型算例进行了方法的正确性验证。

2 方法验证

本节介绍了研究中开展的系列数值实验及结果分析，分别从流量分配、网格类型、计算域截断程度、雷诺数等维度验证了上述出口边界条件，并基于TECFLAM 旋流燃烧器流场模拟验证了所给方法在复杂构型、流动特征中的表现。在2.1 节，针对90°T 形分叉管、60°Y 形分叉管2 种网格类型算例，设定系列流量分配系数，验证了该方法在不同网格类型下流量分配计算的正确性；在2.2 节，针对六面体网格T 形分叉管算例，依次缩减侧面出口段长度，使得出口面流动状态在充分发展和强回流之间变化，考察了出口流动未充分发展时速度场的预测结果。Dong 和Shen［7］指出，流动雷诺数是影响出口边界条件数值稳定性的重要因素，在2.3 节，对比研究了雷诺数在200～50 000 之间变化时该方法的适用性。在2.4 节，介绍了该方法在TECFLAM 旋流燃烧器冷态流动模拟中的模拟验证情况。

2.1 流量分配计算验证

2.1.1 六面体网格算例：90°T 形分叉管

采用Hayes 等［16］提出 的90°T 形分叉 管算例验证六面体网格流量分配的正确性，算例构型如图2 所示。该构型入口段宽度为W，长度为Lin，设定为速度入口边界条件；主出口段长度为Lm，设定为本文中的出口边界条件，流量分配系数为α1；侧面出口段长度为Ls，设定为本文发展的出口边界条件，流量分配系数为α2；垂直于流动平面方向的2 个面设定为对称面，其余部分为壁面边界条件。通过组合入口、出口段宽度、出口流量分配系数以及雷诺数等，可以产生系列复杂的流动行为，如流动分离、再附着等现象。

图2 90°T 形分叉管算例构型及网格剖分示意图Fig.2 Schematic of computational domain of a duct with a 90° T-branch discretized by structured meshes

基于该构型，本节数值实验中重点关注流量分配系数和侧面出口段长度的影响，固定W=1 m，Lin=3W，Lm=10W，入口处速度设定为充分发展状态下近似抛物线分布uin=4x(1-x)，在Ls=10W和Ls=W这2 种 情 况 下，α1∶α2在0∶1.0～1.0∶0 之间变化。采用六面体网格离散计算域，网格数分别为7 464 和3 768，考虑到该设置下雷诺数较小，采用稳态求解器进行模拟。

图3展示了不同流量分配系数下速度大小的分布。图3（a）为Ls=10W的结果，在α1∶α2=0∶1.0 的设置下，相当于主分支出口被封闭，流体全部从右侧分支出口流出，进出口的速度大小及分布非常接近。随着α1∶α2的增加，主分支出口速度值逐渐增加，更多的流体从主分支出口流出，该规律及速度场的分布与预期是相符的。图3（b）展示了Ls=W的结果，从图中可以看出该组速度场计算结果定性合理，速度分布与图3（a）中对应计算域结果非常相似。需要注意的是，在入口段与右侧分支交叉拐角处存在低速回流区，说明尽管该组设置中侧面分支计算域仅为图3（a）结果的1/10，出口流动也远未达到充分发展的要求，但本文提出的出口边界处理方法能很好地预测流量分配结果。关于计算域缩减情况下流场的预测，将在2.2 节中详细阐述。

图3 90°T 形分叉管不同流量分配下的速度分布Fig.3 Velocity distribution of duct case with 90° T-branch at various mass flow ratios

表1 进一步列出了Ls=W，α1∶α2在0∶1.0～1.0∶0 这2 个极端之间变化时，计算收敛时入口流量、主分支出口1 流量、主分支出口2 流量的统计结果，以及实际计算得到的流量分配系数α1和α2。从统计结果来看，采用本文发展的出口边界条件计算得到的流量分配结果与设定值高度吻合，出口流量的最大相对偏差在0.001%量级。

表1 90°T 形分叉管算例流量统计结果Table 1 Mass flow rate statistics results of duct case with 90° T-branch

2.1.2 四面体网格湍流算例：60°Y 形分叉管

采用如图4 所示的三维60°Y 形分叉管算例考察本文方法在四面体网格中的表现。图中管道直径Φ=10 mm，入口段长度50 mm，2 个分叉管呈60°夹角，分叉段长度均为50 mm，分叉管上分支出口记为出口1，流量分配系数为α1，下分支出口记为出口2，流量分配系数为α2。

计算中采用均匀入口边界条件，速度大小为10 m/s，上下2 个分支出口采用本文的出口边界条件，其余边界为无滑移壁面边界条件。采用边界附近棱柱网格、内部四面体网格剖分计算域，包含900 744 个四面体网格，流动处于湍流状态，采用稳态求解器、SST（Shear Stress Transport）k-ω湍流模型进行该算例的计算。该算例可以验证本文算法在四面体网格、复杂流动状态下流量分配和出口回流的处理能力。

图5 绘制了α1∶α2在0∶1.0～0.5∶0.5 范围内变化时Y 形管轴向剖面上的速度分布，计算得到的出口流量和设定出口流量的比较结果如表2 所示。在上分支流量分配系数设置为0 时，计算得到的上分支出口接近于0。随着设定的上分支流量分配系数增加，相应流量逐渐增加，最终上下分支的速度呈对称分布。值得注意的是，在该算例设置下，上下分支起始段会出现一个回流区，其大小随着流量分配系数的增加而不断扩展。出口流量统计结果表明，本算例最大误差出现在α1∶α2=0∶1.0 这种极端流量分配情况下，最大相对误差在0.001%量级，说明本文发展的方法同样适用于典型三维四面体网格、湍流流动情形。

表2 60°Y 形分叉管算例流量统计结果Table 2 Mass flow rate statistics results of duct case with 60° Y-branch

图5 60°Y 形分叉管算例不同流量分配下速度分布Fig.5 Velocity distribution of duct case with 60° Y-branch at various mass flow ratios

2.2 计算域缩减结果一致性验证

本文出口边界处理方法的一个应用目标是，数值仿真中可以根据实际需要将出口边界置于任意位置，出口流动未充分发展、甚至存在回流的情形下数值计算仍然能够满足正确和稳定收敛的要求。为了进一步验证这一特性，研究中针对上文提到的90°T 形分叉管算例开展了系列数值实验进行验证，算例如表3所列。

表3 计算域缩减影响算例和取样位置设置Table 3 Test cases and sampling positions for truncation of computational domain

针对图2 所示的构型，在表3 中，算例1 中设置Lm=10W，Ls=10W。这种情形下主分支出口和右侧分支出口计算域均足够长，满足充分发展的假设，采用常规的出流边界进行计算，可以获得充分发展边界条件下流场解，并得到2 个出口上的质量流量，分别为α1和α2。在此基础上，算例2 采用本文方法处理出口边界条件，流量分配系数保持和算例1 一致，和算例1 的对比结果用于验证本文方法在计算域足够长的情况下和常规出流边界条件的一致性；在算例2 的基础上，进一步缩减右侧分支长度，Ls/W分别取5、3、2、1、0.5，得到算例3～算例7，使得右侧分支出口处流动依次从充分发展状态向回流状态变化，流量分配系数仍保持和算例1 一致。算例2～算例7和算例1 的对比结果，可以验证本文方法在充分发展状态、未充分发展状态以及存在回流状态下的适用性。

图6展示了表3中x= 1.0， 1.5， 3.0， 6.0 m的采样位置，用于定量分析出口边界位置对计算域内部场计算结果的影响。表3 中取样位置所在列“√”表示该算例设置下，当前取样位置在计算域设置范围之内，可进行取样比对。例如算例1中，侧分支长度Ls= 10W，4 个取样位置均位于算例计算域内。但在算例6 中，侧分支长度Ls=W，仅有x= 1.0， 1.5 m 这2 个有效取样位置，而x= 3.0， 6.0 m 这2 个位置因超出计算域不再对比分析。

图6 取样位置示意图（x = 1.0， 1.5， 3.0， 6.0 m）Fig.6 Schematic of sampling locations （x = 1.0， 1.5， 3.0， 6.0 m）

需要特别说明的是，在上述算例设置下，流动的物理特征由流量分配系数保证，在计算域改变时，2 个分支流量分配、物理特性等并未发生变化，重点考察算法能否保证不同计算域选择下结果的一致性。

图7 展示了算例1～算例7 的速度分布云图，为了方便比对，图中仅截选了实际计算域的一部分。图7（a）和图7（b）分别为Ls= 10W构型设置下充分发展边界条件和本文方法中的结果，出口流量分配系数为α1=0.59，α2=0.41。可以看出，在出口流动达到充分发展情况下，本文方法预测的速度场和常规出流边界预测的速度场是定性一致的。图7（c）～图7（g）为Ls/W=5， 3， 2， 1， 0.5 的结果，在右侧分支不断缩减的情况下，入口段、主出口分支以及右侧分支部分的速度分布均和图7（a）中的结果是一致的，即便是Ls/W= 0.5 构型设置、出口处存在强回流情形下，计算中没有出现数值振荡或流场形态的显著变化。

图8 进一步显示了算例1～算例7 在不同取样位置上的速度大小分布，各算例取样设置如表3 和图6 所示。从图中可以看出，Ls/W= 10构型设置、不同取样位置处，充分发展边界条件下的模拟结果和使用本文自由出口边界条件算法得到的速度大小分布基本一致，说明本文方法可以在更小的计算域复现出常规充分发展出流边界条件的模拟结果，即模拟结果与计算域出口边界位置的选择无关。

图8 中x= 1.5 m 和x= 3.0 m 取样处的速度分布显示y= 0.2～0.4 m 之间存在一个速度零点，结合图7 中的速度云图分布，可以看出该速度零点实际上是法向速度发生方向变化的临界点，即该区域存在回流区。图9 绘制了Lm/W= 10、Ls/W= 10 构型设置下2 个分支交叉点附近的流线分布，该流线图明确显示出主出口分支和侧出口分支均存在回流区。Ls/W= 0.5， 1， 2几种构型设置及预测结果说明了本文的出口边界处理方法同样适用于出口边界存在回流的情况。

图7 不同计算域截断情况下速度场云图Fig.7 Velocity contours of duct case with successively truncated computational domain

图8 不同计算域截断程度下典型取样位置的速度大小分布（Lm/W = 10）Fig.8 Velocity profiles of duct case with successively truncated computational domains at various sampling locations （Lm/W = 10）

图9 90°T形管拐角处流线分布（Lm/W = 10， Ls/W = 10）Fig.9 Streamlines distribution at corner of duct case with 90° T-branch （Lm/W = 10， Ls/W = 10）

2.3 流动雷诺数影响验证

Dong 和Shen［7］指出，雷诺数（Re）是影响出口边界条件数值稳定性的重要因素。为验证本方法在不同Re下的适用情况，研究中开展了Re=200～ 50 000 范围内的流场模拟数值实验，其中Re通过修改入口速度uin实现，入口速度均满足uin=Cx(1-x)的分布形式，C取值4、20、50、100、200、500、1 000，依次对应于Re为200、1 000、 2 500、5 000、10 000、25 000、50 000 的情况。构型参数选用Ls/W= 10 和Ls/W= 1 这2 种，用于表征不同出口位置选取情况。算例边界条件设置和上述T 形管保持一致，出口流量分配系数固定为0.6∶0.4。需要指出的是，该系列算例中流动特征变化较大，覆盖了Re= 200 的层流状态到Re= 50 000 的旺盛湍流状态，这里选用匹配于较宽Re范围的SSTk-ω湍流模型。

数值实验结果显示，本文提出的出口边界方法在Re= 200～50 000 范围内均表现出良好的数值收敛性，所有算例未出现数值发散的情况。图10 显示了Re= 25 000 情况下2 种构型对应的速度分布云图，相比于图7 中的结果，高Re下的2 个分支回流区显著扩展，这也是相同构型、采用常规出流边界条件时高Re下更容易出现数值不稳定的主要原因。图11 绘制了不同Re下2 种构型x= 1.0 m 处的速度剖面，其中实线为Ls=10W构型结果，实心方块为Ls=W构型结果，图中为了方便展示不同Re结果，纵轴采用对数坐标系。从图中可以看出，无论是低Re的层流状态还是高Re的旺盛湍流状态，仿真设置的计算域大小均不会影响速度场结果。

图10 Re = 25 000 时2 种构型下速度云图Fig.10 Velocity contours for two configurations with Re = 25 000

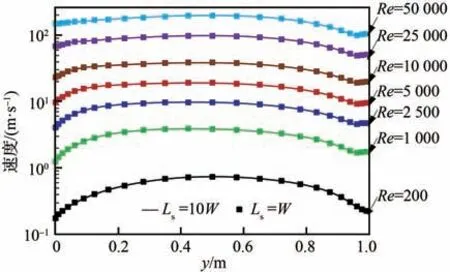
图11 不同Re 下2 种构型x = 1.0 m 处速度分布Fig.11 Velocity profiles at x = 1.0 m for two configurations with various Re

2.4 TECFLAM 复杂旋流算例验证

将1.2 节提出的方法应用于德国TECFLAM旋流燃烧器冷态流场［17-18］的模拟，检验该方法在复杂构型流动特征中的适用性。该燃烧室属于强旋流动，有丰富的冷态流动、甲烷-空气预混燃烧实验数据，被广泛用于数值仿真的结果验证［17-18］，其几何构型和网格剖分结果如图12 所示。TECFLAM 旋流燃烧器主体结构是环形通道包围着一柱状钝体，钝体直径为30 mm，环形通道（内径30 mm，外径60 mm）通空气或空气-甲烷混合物，旋流由环形通道上游一可移动块产生，旋流数可在 0～2.0 范围内连续调节，默认旋流数为0.75。整个燃烧器置于同轴空气伴流中，伴流速度为0.5 m/s。

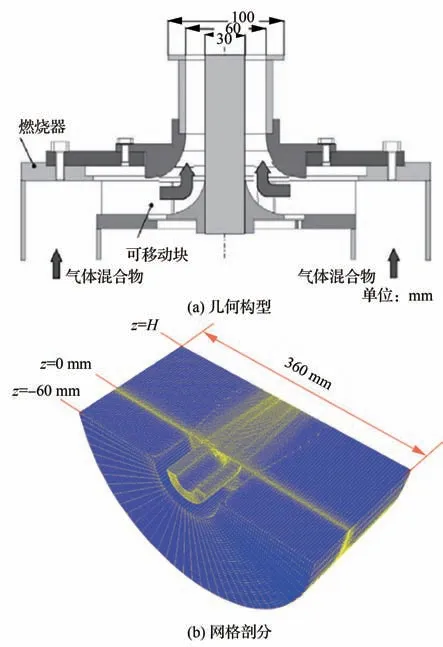
图12 TECFLAM 旋流燃烧器构型和网格剖分Fig.12 Configuration and meshing of TECFLAM swirl burner

计算域选定为燃烧器出口上部空间，出口处高度记为z=0 mm。燃烧室内产生的旋流等效为燃烧室出口处的速度边界条件，即u=-5.23y/r，v=5.23x/r，w=5.0 m/s，其中r为指定点距离中心轴线的径向距离。出口边界位于z=H处，H分别取值120 mm 和360 mm，计算域剖分为45 万网格和110 万网格。前者计算域覆盖了实验和数值研究的重点关注区域（z= 1～90 mm），但出口处存在较强的径向和周向运动，无法直接应用常规出口边界条件；后者出口位于主流区下游较远处，适用于传统边界处理方法，但网格量是前者的2.4 倍。

采用大涡模拟方法、动态Smagorinsky 亚格子应力封闭模型，基于上述2 种计算域模拟TECFLAM 冷 态 流 场，将z= 1， 10， 20， 30， 60 mm 处时均速度3 个分量的预测值与实验结果比对，结果如图13 所示。其中，实验值取自文献数据［17-18］，设置1 对应于H= 120 mm 的计算域，设置2 对应于H= 360 mm 的计算域。在H= 360 mm 时，速度分量的分布说明了计算域中的流动特征：气体从喷口喷出后，切向分量和轴向分量相当（～ 5 m/s），主导整体运动。沿着径向方向，切向速度分量先增加后减小，并在某个径向位置处出现最大切向速度，构成旋涡区。随着流动的发展，旋涡区域逐步沿着径向方向发展（～ 1 m/s）。图13 中设置2 和实验值结果表明，不同高度处速度3 个分量的预测值与实验值符合得较好。当H从360 mm 减小到120 mm 时，计算域大幅缩减，本文方法能够保证稳定收敛。从对比结果来看，在z= 1～60 mm 范围内，除了部分流场变化剧烈区域速度预测值出现一定的偏差，速度3 个分量的预测值仍然和实验数据保持较高的一致性。

图13 TECFLAM 旋流燃烧器模拟的时均速度分布与实验结果［17-18］对比Fig.13 Comparison of time-averaged velocity distribution in TECFLAM swirl burner simulation with experimental［17-18］ data

3 结 论

本文发展了一种基于质量流量分配系数的多出口计算域边界条件处理方法，实现了不可压缩流动模拟中多出口边界、存在回流情形的高效、稳定模拟，并基于自主研发的高性能计算流体数值模拟软件验证了该方法的有效性，主要结论如下：

1）针对典型六面体网格、四面体网格算例，该方法实现了出口质量流量分配系数在0～1.0范围内的稳定模拟，计算得到的质量流量分配系数和设定值最大相对偏差在0.001%量级。

2）在保持出口流量分配系数不变的情况下，该方法正确预测了出口流动未达到充分发展、存在回流或旋流下的流场，出口边界位置对计算结果的影响很小；在计算域出口流动达到充分发展状态时，其预测结果和常规充分发展边界条件的结果一致。

3）通过2 种典型构型设置、系列Re数值实验，验证了该方法适用于Re处于200～50 000 范围、出口流场未充分发展或存在回流的情形，覆盖了低Re层流到高Re旺盛湍流。

4）使用TECFLAM 旋流燃烧器冷态流场大涡模拟验证自由出口边界条件算法，结果表明计算区域缩减至1/3 后模拟仍能保证稳定收敛，预测值和实验数据保持较高的一致性。相比于使用常规出口边界的方法，本文的自由出口边界条件算法支持仿真人员根据需要选择计算域，可显著减小数值计算开销。