神经网络宽度对燃烧室排放预测的影响

王志凯，陈盛，范玮

1．中国航发湖南动力机械研究所，株洲 412002

2．西北工业大学 动力与能源学院，西安 710129

航空发动机燃烧室的发展方向是高温升、低污染，特别是对于民用航空发动机，NOx、CO、UHC（Unburned Hydrocarbon）和冒烟排放的适航标准不断提高、指标更加苛刻，同时在国家“碳达峰、碳中和”的战略背景下，对低排放燃烧室设计提出了更高的要求。

目前的降排放方法包括：① 发展低排放燃烧技术原理，如贫油预混预蒸发（Lean Premixed Prevaporized，LPP）［1］、贫 油 直 接 喷 射（Lean Direct Injection，LDI）［2］、富 油-淬 熄-贫 油（Rich-Quench-Lean，RQL）［3］等；② 创新燃烧组织实现方式，如中心分级燃烧（Center-Staged Combustion，CSC）［4］、驻 涡 燃 烧（Trapped Vortex Combustion，TVC）［5］、弱旋燃烧（Low Swirl Combustion，LSC）［6］等；③ 采用新燃料，主要是用低碳或零碳燃料代替传统的航空煤油，如生物质燃料［7］、氢燃料［8］、混合燃料（如氢气+甲烷［9］）等。

燃烧室排放的传统研究途径有经验公式、数值仿真、单头部/扇形/全环/整机试验等，但用于预估排放的经验公式普遍存在函数形式复杂、拟合精度有限、适用范围较窄等问题；高保真的数值仿真在时间和长度尺度上涉及到流动、雾化和燃烧化学反应的非线性耦合，需要大量高精度的试验数据进行模型标定；台架试验周期长、成本高，且单头部的排放试验结果对工程指导有限，并不能反映全环或者整机上的真实情况。近年来热门的机器学习为燃烧室排放快速预估和新知识新规律的挖掘提供了一种新的研究范式。神经网络［10-13］作为机器学习的重要工具，由于具有自适应、自学习、非线性映射和容错等优点，逐渐在燃烧室排放研究领域得到应用。文献［14］综述了机器学习在燃烧科学领域如化学反应、燃烧建模、燃烧测试、发动机性能预测和优化以及燃料设计等方面的应用研究。文献［15］建立了以发动机转速和负载为输入，燃油消耗和排放为输出的神经网络模型，试验测量数据和模型预测对比表明训练良好的网络能够预测发动机排放。文献［16］基于神经网络和支持向量机进行了燃气轮机NOx排放预测，提出了一种构建排放预测黑箱模型的遗传算法，该算法能自动确定预测燃气轮机NOx排放的多层感知机神经网络的最优拓扑。文献［17］建立了神经网络模型来预测发动机性能和燃烧排放特性。文献［18］建立了一种利用交互信息和反向传播神经网络估算氮氧化物排放的方法，平均绝对偏差和均方根误差降低了约15%，减少了对特征选择专家知识的需求，计算成本较低。文献［19］基于大量运行数据，采用神经网络对燃气轮机NOx排放及燃烧稳定性参数进行了建模，针对影响燃烧性能的参数进行了敏感性分析。

深度神经网络（Deep Neural Networks，DNN）一直是国内外研究的热点，深层结构神经网络和学习也在许多领域得到应用［20-24］。虽然深度结构网络非常强大，但普遍被极度耗时的训练过程所困扰。与此同时，为了在应用中获得更高的精度，深度模型不得不持续地增加网络层数或者 调 整 超 参 数 个 数。Chen 和Liu［25］2018年 提 出了宽度学习系统（Broad Learning System，BLS）作为深度学习网络的替代方法。作为一种新型的扁平式神经网络结构，宽度学习系统可以将新加入的数据以有效和高效的方式更新系统。和深度网络相比，宽度网络省去了层与层之间的耦合，因此具有快速、高效的特点，可以在时间效率和性能上达到非常好的平衡。随着机器学习的不断发展，宽度学习这种不需要深度结构的高效学习系统得到了研究者的青睐。

网络深度和网络宽度是神经网络结构框架中的2 个重要维度，如何在二者之间寻求有效的平衡，在低的计算资源消耗下实现神经网络模型的高精度预测是需要研究的重点。网络深度的作用是逐层抽象，不断精炼提取知识特征；网络宽度的作用是让每一层都学习到更加丰富的特征，网络太窄每一层挖掘的信息有限，网络再深都不能有效地提取到足够的信息向下传递。因此选择一个合适的网络宽度对神经网络模型的高效精确预测至关重要。但针对网络宽度的研究远不如网络深度多，目前主要依靠经验法则［26-28］来选取网络宽度。本文基于全环燃烧室排放试验数据，建立了输入工况参数与排放输出的映射关系的神经网络预测模型，通过横向拓展的方法研究了网络宽度对模型预测精度和拟合优度的影响，确定了最优网络宽度，并验证了基于最优宽度的神经网络排放预测模型的准确性和泛化性，为燃烧室方案设计阶段排放性能指标的快速评估和精确预测提供新的思路和方法工具。

1 试验系统和研究方法

1.1 试验系统

燃烧室排放试验系统主要包括进气系统、排气系统、循环水系统、冷却气系统、燃油系统、电气及控制系统、测试系统、燃烧室全环试验件等，如图1 所示。其中，燃烧室全环试验件主要由扩压器、外机匣组件、内机匣组件、火焰筒、旋流器、火焰筒内外环转接段、燃油分配器、双油路离心喷嘴、燃油总管及点火器等组成。

图1 燃烧试验系统示意图Fig.1 Schematic of combustion experimental system

燃烧室进口空气流量（ma3）采用标准流量喷嘴测量，燃油流量（mf）采用质量流量计测量；进口总压（Pt3）通过3 支沿周向分布的单点总压管测量，共3 点；进口总温（Tt3）通过3 支沿周向分布的单点热电偶进行测量，共3 点；出口总压（Pt4）通过3 支沿周向均布的梳状总压耙进行测量，每支3 个测点，测点沿径向按等距离分布；出口总温（Tt4）通过3 支沿周向均布的梳状热电偶进行测量，每支4 个测点，测点沿径向按等距离分布。采用燃气分析系统测量排气污染物，燃气采样探针1 支，沿径向布置3～5 点，燃气采样探针测点的径向分布按等环面设计，安装在燃烧室出口旋转机构上，便于对火焰筒出口环面进行测量。

排放试验工况具体是进口温度Tt3为370～820 K，进口压力Pt3为0.2～1.8 MPa，供油流量mf为0.016～0.4 kg/s，油 气 比FAR 为0.007～0.029，录取各个状态燃烧室出口燃气中CO 和NOx的浓度，排放结果换算成排放指数（EICO、EINOx），单位为g/（kg 燃油）。试验用油为3 号喷气燃料（RP-3），试验测试精度见表1。

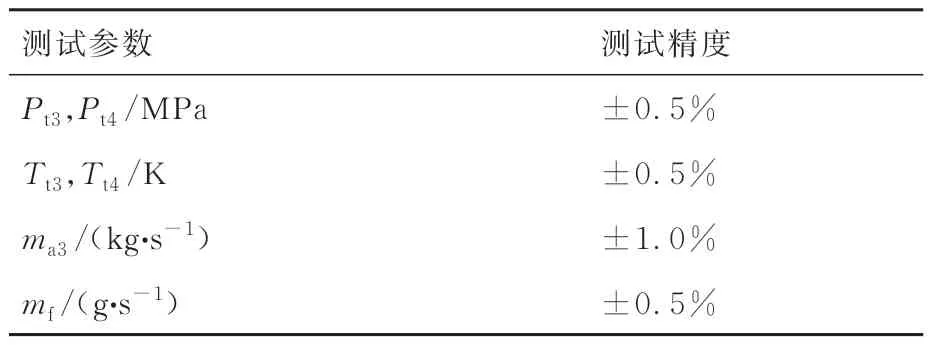
表1 测量参数和测试精度Table 1 Measurement parameters and test accuracy

1.2 神经网络

人类的大脑由数十亿相互连接的神经元组成，每个神经元网络由一个细胞体、一组称为树突的纤维和一个轴突组成，树突作为神经元的输入通道，而轴突作为输出通道。因此，神经元通过树突接收输入信号，而树突又与其他邻近神经元的（输出）轴突相连。通过这种方式，一个足够强的电脉冲可以沿着一个神经元的轴突传递给与其相连的所有其他神经元［12］。这使得信号可以沿着人脑的结构传播。神经网络可以认为是函数逼近算法，当有许多输入值和相应的目标输出时，神经网络将寻求近似存在于两者之间的映射。2 个神经元之间的每个连接都被赋予一个权重，这个权重作用于通过网络的数据流。

神经网络是一种应用类似于大脑神经突触连接的结构进行信息处理的数学模型，二者相似性主要体现在以下3 方面：① 均由大量相互连接的神经元网络组成；② 寻求通过网络传播信息；③ 接收来自邻近神经元的成套刺激，并将这些刺激映射到输出，输入到下一层神经元。

在神经网络中，反向传播（Back Propagation，BP）神经网络是一种信号正向传播、误差反向传播的前馈神经网络［29-31］，2 个过程之间相互交替可得到加权向量与阈值，从而使网络的误差函数最小。BP 神经网络由一个输入层、一个或多个隐含层、一个输出层组成，每一层由几个称为神经元的节点组成，一层神经元通过它们的权重直接连接到下一层。当将输入值xi输入网络时，输出值y是输入值经过激活函数fact变换后的加权和［32］，可表示为

式中：xi为来自第i个神经元的输入；wi为第i个神经元的连接权重值；b为偏置。

隐含层的神经元采用光滑可微S 型对数函数sigmoid 作为激活函数，表达式为

若单隐层前馈型神经网络连续，且传递函数为sigmoid，则网络可以逼近任何一个复杂的连续映射［33］。因此，为了快速实现对网络宽度的影响研究，本文采用基于单隐含层的BP 神经网络构建网格框架。输入层的网络宽度为输入参数的个数4，输出层的网络宽度为输出参数的个数2，通过横向拓展的方法确定隐藏层的网络宽度，即隐藏层神经元的个数。结合实际应用范围，确定了网络宽度为2n（n=2，3，4，5，6，7）的横向拓展方案开展对比研究，通过评估拟合优度和误差分析，以期获得本文的最优网络宽度。神经网络模型结构见图2，迭代流程见图3，图中MSE 为均方误差，Adj.R2为校正决定系数。

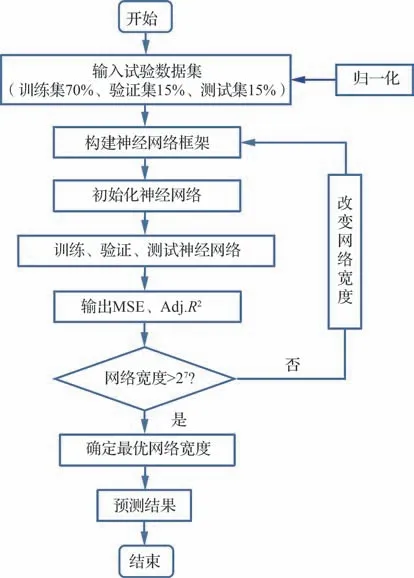
图3 神经网络迭代流程Fig.3 Procedure of neural network training

神经网络的训练函数为trainlm 函数，即采用L-M（Levenberg-Marquard）算法随机把输入向量和目标向量划分成训练集、验证集和测试集，该算法是牛顿法的改进，通过直接计算海森矩阵减少了训练步数，使得网络快速接近目标函数。L-M 算法的迭代方程为

式中：x(k)、x(k+1)分别为第k、k+1 次迭代神经网络中各层之间权值与阈值组成的向量；e为网络各层的误差向量；μ为系数；J为雅克比矩阵；H为海森矩阵。

为了消除特征参数量纲和量纲单位差异的影响，加快学习算法的收敛速度，将所有数据集参数在输入网络前进行归一化处理，使得数据统一映射到［0，1］区间上。归一化（Normalized）方法为

式中：x'为归一化处理后的数据；x为原始数据；xmax为最大值；xmin为最小值。

本文将排放试验录取的210 组试验数据作为真实样本，按70%、15%、15%随机划分为训练集、验证集和测试集。其中训练集用于拟合神经网络模型，挖掘映射关系，不断提高模型精度；验证集用来评估模型预测的好坏，并调整对应的参数；测试集用于检验模型对未参与训练的试验数据的匹配程度，用作网络泛化的完全独立测试，客观评价由训练集训练出的模型的泛化能力和精度。

选取燃烧室进口空气温度（Tt3）、进口空气压力（Pt3）、供油流量（mf）和油气比（FAR）4 个主要参数作为神经网络的输入节点，以排放指数EICO和EINOx为输出评价指标进行神经网络训练。

2 结果与分析

2.1 网络宽度优化

为了研究网络宽度对神经网络预测模型精度的影响，进而确定适合本文应用实际的最优网络宽度，需要对不同网络宽度下模型的拟合优度和预测精度进行对比分析。

采用均方误差（Mean Squared Error，MSE）表征模型预测值与试验值之间的误差，表示为预测值与试验值差的平方和的均值，该值越小代表预测效果越好。随着样本数量的增加，常用的决定系数R2必然增加，无法真正定量说明拟合优度。本文采用校正决定系数（AdjustedR2，Adj.R2）定量评估神经网络模型的预测值与试验值之间的拟合优度，Adj.R2是经自由度修正后的决定系数，抵消了样本数量对R2的影响，做到了真正上在［0，1］范围内越大，拟合优度越高。

MSE、R2和Adj.R2的表达式为

式中：yexp和ypred分别为试验值和预测值；为试验值的平均值；n为样本总数；p为特征数。

图4 为不同网络宽度下训练集、验证集和测试 集 对 应 的MSE 和Adj.R2对 比。由 图4（a）可见，MSE 整体呈现先减后增的趋势，当网络宽度为24时训练集、验证集和测试集的均方误差均较小，而且随着网络宽度的继续增大，模型预测误差显著增大，表明存在最优的网络宽度使得神经网络预测模型的误差最小。由图4（b）可见，Adj.R2整体呈现先增后降的趋势，当网络宽度为24时验证集和测试集的校正决定系数均最大，且训练集的校正决定系数也较大，随着网络宽度的持续增大，校正决定系数开始减小，表明存在最佳的网络宽度使得校正决定系数最大。

图4（a）和图4（b）显示，随着网络宽度的增加，训练集的MSE 逐渐减小，Adj.R2逐渐增大，表明训练的模型精度和拟合优度逐渐得到优化，原因是网络变宽，位于输入层和输出层之间的隐藏层具有更多的神经元节点进行数据挖掘，使得模型学习能力增强，模型有更多的容量去达到更好的预测效果。但是验证集和测试集的精度随网络宽度增加先改善后变差，当网络宽度太大（如26和27）时，训练集的预测精度和拟合优度很高，但验证集和测试集急剧变差，出现了过拟合现象，即神经网络在训练样本中表现优越，在验证集和测试集数据中表现不佳，其原因是网络宽度的增加使得网络结构变得复杂，数据挖掘、特征提取和学习能力变强，以至于在训练集数据中学习到了一些统计噪声（实际上这部分信息仅是局部数据的统计规律），并将其认为是一般规律，从而导致模型泛化能力下降，一般采用的方法就是降低模型复杂度，比如减小网络宽度，这也解释了存在最优网络宽度的原因。

综合图4 可知，网络不能太宽或者太窄，存在一个合适的网络宽度使得模型误差和校正决定系数均达到最佳，对于本文研究来说该最优宽度为24。

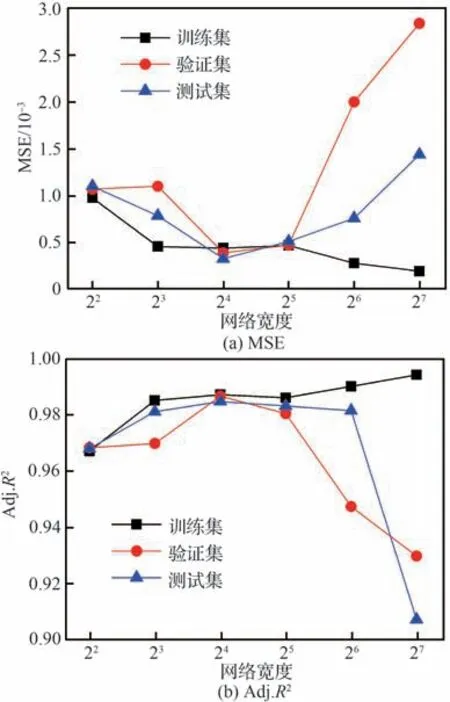
图4 网络宽度对MSE 和Adj.R2的影响Fig.4 Effect of network width on MSE and Adj.R2

2.2 模型验证

基于2.1 节获得的最优网络宽度进行神经网络模型训练，用来预测燃烧室排放指数。图5 和图6 显示了训练集、验证集和测试集上的CO 和NOx排放指数预测值与试验值对比，图中“′”表示根据式（5）得到的归一化值。由图可见，校正决定系数均＞0.986，而且拟合关系式趋于y=x，即CO 和NOx排放指数的预测值和试验值拟合优度高，表明基于最优网络宽度建立的神经网络预测模型能够很好地挖掘输入参数与排放之间的复杂映射关系，实现了对燃烧室CO 和NOx排放值的准确预测。

图5 EICO预测值与试验值对比Fig.5 Comparison of EICO from prediction and experiment

图6 EINOx预测值与试验值对比Fig.6 Comparison of EINOx from prediction and experiment

为了直观分析模型误差的分布状态，绘制了如图7 所示的误差直方图，其中横坐标为CO 和NOx归一化排放指数试验值与预测值的差值，是误差区间的中位数。误差直方图将模型误差存在的区域分为了20 个区间，以柱形的高度来表示各区间对应样本出现的频次。由图可见，试验值和预测值的误差主要分布在横坐标为-0.06～0.083 之间，绝大部分误差分布在-0.025～0.028 之间，集中分布在0 误差线左右，表明基于最优网络宽度的神经网络排放预测模型误差较低，具有很高的精度，可作为给定进口工况参数下燃烧室排放指数的预测工具。

图7 预测值与试验值的误差直方图Fig.7 Error histogram of prediction and experiment results

2.3 敏感性分析

机器学习和燃烧物理学是2 种不同的研究范式。如图8 所示，机器学习是一种数据驱动的方式，而燃烧物理是一种规律驱动的方式，因此机器学习可理解为一种黑盒子模型，而燃烧物理学是一种白盒子模型。在交叉应用中可以用机器学习帮助处理大量的燃烧数据，从而发现这些数据背后隐藏的模式；也可以用燃烧物理的知识工具理解机器学习，或者设计更好的机器学习模型。

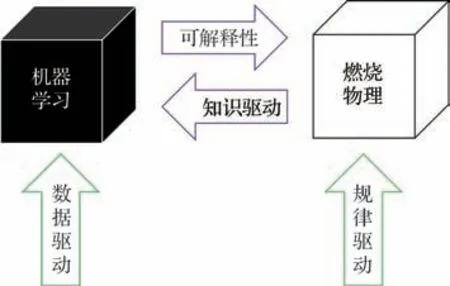
图8 机器学习和燃烧物理学的关系Fig.8 Relationship of machine learning and combustion physics

随着神经网络预测应用领域的不断拓展，作为制约机器学习应用的瓶颈，可解释性（Interpretability）问题越来越受到重视。可解释性可以帮助人类理解机器学习系统的特性，推断系统内部的变量关系，进而为分析参数之间的相关性提供辅助信息［34］。

在神经网络的可解释性研究方面，通常采用敏感性分析方法。敏感性分析是用于定量描述模型输入变量对输出变量的重要性程度的方法［35］，用于分析待解释样本的每一维特征对模型最终结果的影响［36］。典型的敏感性分析方法有基于连接权、基于统计和基于扰动分析3 类［34］。本文基于连接权采用2.1 节构建的神经网络模型开展敏感性分析，分析燃烧室输入参数对排放指数的影响关系，确定输入参数对输出目标的影响程度。

针对已建立的神经网络模型，利用式（9）［19］进行CO 和NOx排放指数2 个参数的敏感性因子计算，然后通过式（10）得出4 个输入参数对同一排放指数的整体影响占比大小。

式中：Si，k为第i个输入变量对第k个输出变量的敏感性因子；Nh为隐藏层数目；1 [ 1+exp(-wm，i)]为输入层与隐藏层连接权重经sigmoid 函数激活后的值；wk，m为隐藏层到输出层之间的连接权重；k=1 和k=2 分别代表输出变量为EIco和EINOx。

图9 显示了基于敏感性分析的输入参数对排放指数的影响占比。由图可见，在本文试验工况范围内，4 个输入参数中Pt3对CO 排放的影响最大，影响占比达到62%，其后依次是Tt3、mf及FAR；Pt3对NOx排放的影响最大，影响占比为43%，Tt3的影响次于Pt3，占比为26%，随后依次是FAR 及mf，且二者影响程度接近，主要原因是相同进口空气温度下，研究不同进口空气压力的影响时均保证了相同的进气流量，因此油气比和供油流量呈线性相关。

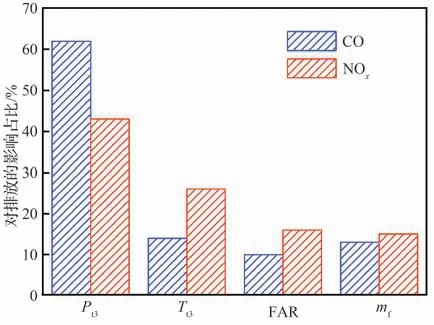
图9 输入参数对输出值的影响程度Fig.9 Analysis of sensitivity of various input parameters to emission output

下面以部分试验工况为例，结合燃烧物理机理和试验现象对构建的神经网络模型预测结果进行探讨。要分析排放受供油流量影响的规律和内在原因，首先需要了解本文试验所使用的双油路离心喷嘴的供油流量控制规律和雾化特性曲线（图10）。由图10 可见，双油路离心喷嘴的供油过程可分为3 个典型阶段。

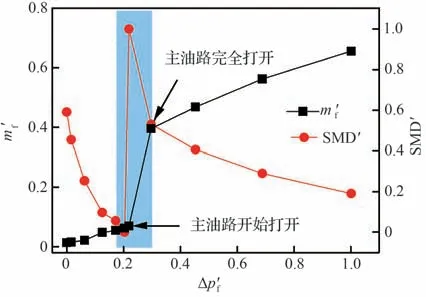
图10 流量和雾化特性曲线Fig.10 Flow rate and spray characteristic curves

第1 阶段：由于设计时副油路的打开压力低于主油路，故在供油压差较小（即横坐标归一化供油压差Δp'f＜0.2，对应的纵坐标供油流量m'f＜0.1）的区间内，当供油压差达到副油路打开压力时，副油路首先打开并持续工作。这个阶段内，雾化质量随供油增加逐渐改善，索太尔平均直径（Sauter Mean Diameter，SMD）呈现减小的趋势。

第2 阶段：随着供油压差逐渐增大，达到主油路打开压力（即Δp'f=0.2，对应的m'f=0.1）时，主油路开始打开，但打开过程较慢，需要持续增加供油直至主油路完全打开（即Δp'f=0.3，对应的m'f=0.4），主油路逐渐打开的过程使得原先副油路雾化很好的油雾场由于主油路大液滴的加入，造成燃油雾化质量突然恶化。

第3 阶段：主油路完全打开后（即Δp'f＞0.3，对应的m'f＞0.4），主副两油路共同工作，燃油供给达到相对稳定的状态，且SMD 随供油继续增加而减小。

图11 给出了不同试验工况下试验值和神经网络预测结果的变化曲线。图11（a）为归一化进口空气温度（Tt'3）为0.17 时，不同归一化进口压力（P't3）对应的归一化CO 排放指数（EI'CO）变化曲线。 由图可见，EI'CO随m'f或归一化油气比（FAR′）的增大先减后增，这是因为，由图10 可知当m'f＜0.1 时，双油路离心喷嘴的主油路还未打开，只有副油路工作，且随着供油流量增大，雾化质量逐渐改善，液雾平均粒径减小，燃油蒸发变快，燃烧反应加快，燃烧更充分，生成的中间产物CO 逐渐减少。当m'f达到0.1 时，主油路开始打开，但在图11（a）所示供油范围内主油路未完全打开，在此区间内，由图10 可知雾化质量变差，很容易引起燃烧不充分，导致燃烧中间产物CO增加。

图11 排放指数随输入参数变化曲线Fig.11 Variation curves of emission index with input parameters

图11（b）为Pt'3=0.75 时，不 同Tt'3对应的归一化NOx排放指数（EI'NOx）变化曲线。由图可见，EI'NOx随m'f或FAR′的增大而减小，且变化越来越缓和。该现象与常规变化规律不同，主要原因是对于该燃烧室，燃油雾化对NOx排放的影响强于因油气比增大引起的燃烧区温升对NOx排放的影响。具体地，图11（b）所示的供油范围处于图10 曲线的第3 阶段（双油路工作状态），图10 显示m'f＞0.4 时随着供油流量的增大，SMD 逐渐减小且存在逐渐缓和的趋势，一方面SMD 的减小有利于降低NOx排放［37］，另一方面雾化品质改善，火焰筒内燃油分布更均匀，有利于避免局部燃油集中导致的局部高温区出现，从而降低NOx，直至最后维持在一个较低的恒定水平。

此外，图11（a）还显示，EI'NO随P't3的增大而减小，原因是在低FAR 时，压力增大促进了化学反应，加速CO 向CO2的转化；在高FAR 时，压力增大抑制了CO2的化学裂解。图11（b）还显示，EIN'Ox随Tt'3的增大而增大，这是因为NOx的形成依赖于燃烧反应温度，进口温度升高有助于强化燃烧，主燃区温度升高，NOx排放增加。

3 结 论

1）基于录取的全环燃烧室排放试验数据，构建了以燃烧室Tt3、Pt3、mf和FAR 为输入，CO 和NOx排放指数为输出的神经网络模型，能够很好地挖掘输入参数与排放指数之间的映射关系。

2）神经网络宽度对燃烧室排放预测影响较大，存在一个最优的网络宽度值，使得神经网络预测模型的拟合优度和预测精度达到最佳，本文最优的网络宽度为24。

3）拟合优度、误差分析和敏感性分析验证了基于最优宽度的神经网络排放预测模型的准确性和泛化性，实现了对燃烧室排放的高效精确预测，可作为给定工况参数下燃烧室排放指数的预测工具。

4）基于敏感性分析的神经网络可解释性研究显示，在本文试验工况范围内，进口空气压力对CO 排放的影响最大，其后依次是进口空气温度、供油流量及油气比；进口空气压力对NOx排放的影响最大，其后依次是进口空气温度、油气比及供油流量。