基于代数结构视角对轻量分组密码WARP 的积分分析

邢朝辉 张文英 曹梅春

1 （山东师范大学信息科学与工程学院 济南 250358）

2 （山东交通学院理学院 济南 250357）

3 （山东管理学院信息工程学院 济南 250357）

（3613452@qq.com）

无线传感网络（wireless sensor network, WSN）与射频识别技术（radio frequency identification, RFID）在工业互联网中有着广泛应用，工业互联网的底层集成和使用了大量资源受限的终端设备，例如传感器、智能仪表、可编程控制器等，所生产的海量数据的安全传输是保障工业互联网安全运行的关键，于是，专门为WSN 及RFID 设计的轻量级加密算法应运而生.轻量级密码算法的早期典型代表是PRESENT[1]和LBlock[2-3]，近几年新提出的算法有GIFT[4]，WARP[5].

WARP 算法是由Banik 等人[5]在SAC 2020 会议上提出来的轻量级分组密码，它具有硬件面积小、能耗低的特点，在大多数典型硬件配置下，是目前128b分组密码中硬件面积最小的. 另外，它在软件实现上也有非常好的表现：在8b 微处理器上进行软件实现，在可接受的执行时间内，具有非常有竞争力的短代码长度和极低的RAM 能耗；在高端处理器上使用SIMD 进行软件实现时，实现效率非常高，适用于计算能力弱、存储空间小等资源受限的物联网加密环境. 多方安全性评估是新密码算法在投入市场之前必有的检验. 设计者[5]给出了一个21 轮不可能差分区分器和一个20 轮积分区分器；文献[6]给出了一条19 轮差分路径和21 轮密钥恢复攻击；文献[7]基于21 轮区分器进行了24 轮矩形攻击，还给出了一个全轮的相关密钥差分攻击. 相关密钥攻击假设攻击者可以反转密码机里密钥的某些比特位，但在实际应用中攻击者不具有这个权限，该攻击对密码算法安全性不形成实际威胁. 设计者在算法描述文档中曾声明不考虑相关密钥攻击的威胁. 本文用积分分析的方法对WARP 进行了单密钥情境下的有效攻击.

积分攻击是针对分组密码算法最有效的攻击方法之一，它是由Daemen 等人[8]在评估分组密码SQUARE 时首次提出. 在2002 年FSE 会议上，Knudsen等人[9]对此类攻击技术进行了理论上的统一，称之为积分攻击. 积分攻击的关键是寻找一个覆盖轮数尽可能多的积分区分器. 传统的积分区分器构造方法主要有2 种：一是通过评估积分性质的传播进行构造的方法；二是代数次数估计方法. 在2015 年欧密会上，Todo[10]提出了可分性的概念，它是积分性质的推广，它的提出为积分区分器的构造带来突破性的进展. 可分性在构造积分区分器时考虑了更多加密原语的代数信息，更准确地描述了积分性质，从而改进了许多加密算法的积分攻击结果[11-14]. 此外，可分性还可以与多种自动化搜索工具相结合，实现对可分性的自动化搜索[15-18]. 但是当密码算法的分组规模较大时，对可分性的搜索会受限于计算复杂度和存储复杂度. 目前，一些研究从代数结构层面进行宏观分析和可证安全性探索[19-20]，在某些算法的分析上取得了优于可分性的积分分析结果，例如，在文献[20]中，作 者将SPN（substitution permutation network）密码算法多轮的加密变换表示成上的多变量多项式，其中b为S 盒的输入比特数，研究多变量多项式中出现次数较少的输入字可能带来的密码学性质得到了SKINNY 的10 轮积分区分器，时间复杂度低于使用可分性得到的积分区分器.

本文中总体框架采用Feistel 结构，且F 函数采用SP（substitution permutation）结构的分组密码称为Feistel-SP 类分组密码[21]. 本文的研究动机来源于Zhang 等人[20]的工作以及WARP 算法的问世. 借鉴文献[20]方法的核心思想，本文也把输出字写成输入字的多变量多项式，基于多变量多项式中输入字的出现次数讨论分组密码基于代数结构的积分性质. 在研究过程中，发现了某种代数结构的密码算法具有积分性质，并通过分组密码S 盒差分分布表（difference distribution table, DDT）的特性：|{x| x∈为偶数，证明了这一性质.利用该性质，可以找到某些覆盖轮数更多的积分区分器，从而改进利用代数结构进行积分分析的方法.另外，通过对几个Feistel-SP 结构分组密码的结构进行分析，发现此分析方法可从分析SPN 分组密码扩展到分析Feistel-SP 分组密码上，并将改进的积分分析方法应用到Feistel-SP 分组密码WARP 算法上，构造了2 个数据复杂度为2116的22 轮积分区分器，基于该区分器给出26 轮积分攻击，而WARP 设计者只给出1 个数据复杂度为2124的20 轮积分区分器，且认为最多可进行21 轮攻击. 为了验证所给方法和理论的正确性，对用此方法所构造的18 轮积分区分器做了实际实现，其复杂度为232，耗时7.1 h. 将本文的结果与之前所有单密钥情境下的攻击结果进行了对比，如表1 所示. 结果表明，本文的积分攻击是目前对WARP 可验证的最好的密钥恢复攻击结果.

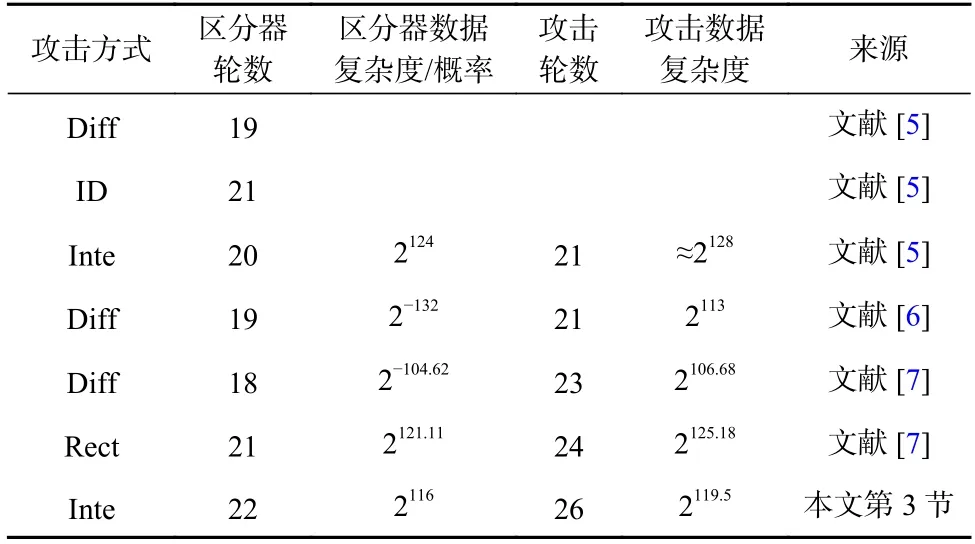
Table 1 Key-Recovery Attacks on WARP in the Single-Key Scenario表1 单密钥情境下对WARP 的密钥恢复攻击

1 预备知识

本节简要介绍积分分析方法、文中用到的基本符号和定义，以及WARP 算法描述.

1.1 积分分析

积分分析的主要思想是选择特定的明文集合，一般是对明文的某些比特位进行遍历（称为活跃比特），其余的明文比特位固定（称为常量比特），对选定的明文集合进行加密，对得到的所有密文值逐比特位异或求和（称为积分），若积分中的某些比特位恒为0（与密钥和常量比特无关），则称这些比特位是平衡的，即H:而对于均匀分布的随机变量而言，积分的每一比特位等于0 的概率为1/2，攻击者通过积分值的非随机性将目标算法与随机置换区分，并恢复某些密钥比特位.

1.2 二元关系

定义1[22]. 由2 个元素x和y（x，y可属于不同集合）按一定顺序排列成的二元组称作一个有序对，记作〈x,y〉,其中x是第1 元素，y是第2 元素.

定义2[22]. 如果一个集合满足条件之一：1） 集合非空，且它的元素都是有序对；2） 集合是空集. 则称该集合为一个二元关系.

定义3[22]. 设U，G为二元关系，U和G的复合记作U°G，其中U°G={〈x,y〉|∃t使得〈x,t〉∈U∧〈t,y〉∈G}.

1.3 WARP 算法描述

因为在本文中S 盒细节以及轮常数取值不影响对算法的分析，所以忽略S 盒细节及轮常数描述. 解密过程与加密过程类似，只是将置换π换成π−1，轮常数逆序使用. 具体加密过程为：

首先，将128 b 明文X加载到128 b 的初始 状态Q0中，然后迭代运行41 轮. 当轮数r=1, 2, …, 40 时，轮函数包含4 个步骤.

解密过程略. 关于WARP 算法的详细描述，请参见文献[5].

2 利用代数结构构造积分区分器的框架

首先简要回顾文献[20]中利用代数结构构造SPN 分组密码积分区分器的主要思想：把明文字（密文字）用中间状态字的多变量多项式表示出来，通过统计中间状态字在多变量多项式中出现的次数来构造积分区分器. 给定的分组密码的代数结构通过多变量多项式体现出来，用以评估抵抗攻击的安全性.我们发现该思想同样适用于Feistel-SP 结构分组密码，并且攻击效果更佳. 该文献指出可用S 盒的置换性质构造积分区分器，定理1 描述了该性质.

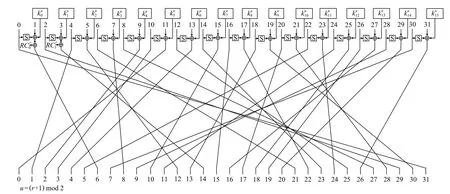
Fig.1 The round function of WARP图1 WARP 算法的轮函数

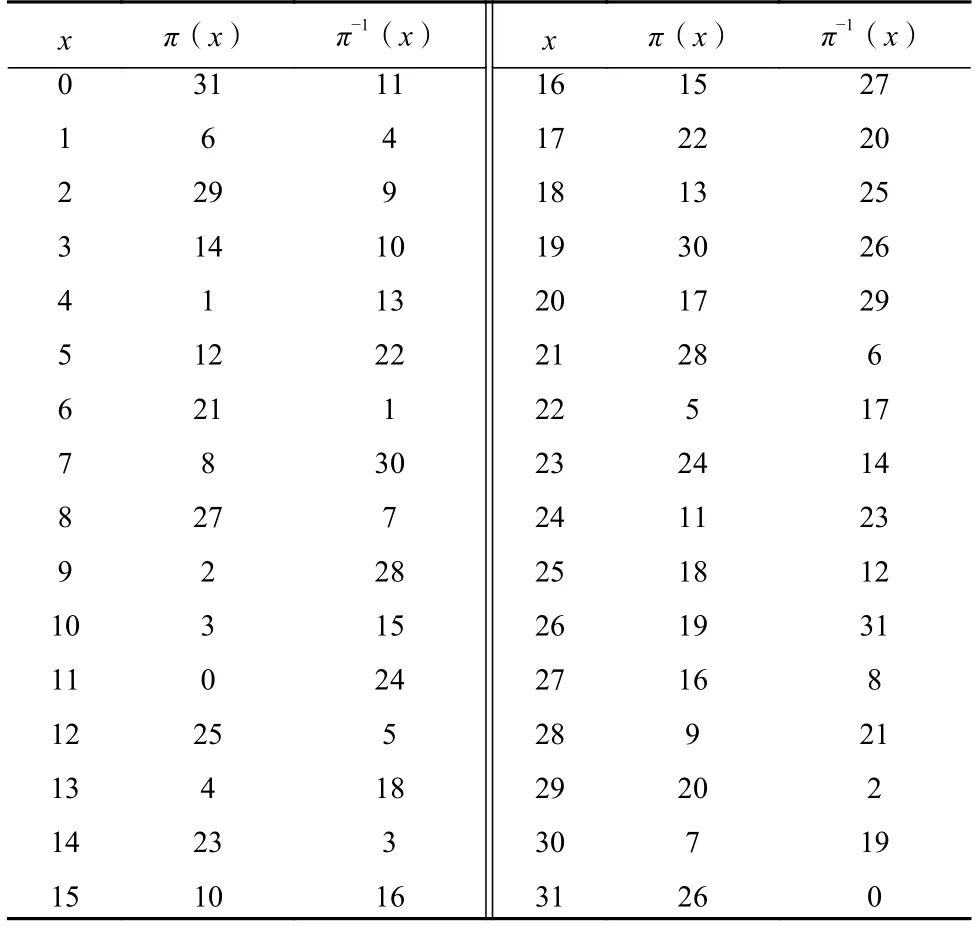
Table 2 Shuffle π and π−1 of WARP on 32 Nibbles表2 WARP 算法中面向32 个半字节的置换π 和π−1

本文将用$（x）表示置换Sn−1（…S1（S0（x⊕c0）⊕c1）…⊕cn−1）. 定理1 表明，若中间状态字在密文字的表达式里只出现1 次，则当中间状态字遍历时，密文字是平衡的. 在研究过程中，发现了某种代数结构的密码算法具有积分性质，可以用中间状态字的多变量多项式进行判别，并将某些积分区分器扩展至更多轮数，见定理2.

定理2 表明，虽然中间状态字在密文字里出现2 次，但是若以S（S（x）⊕S（x⊕u）⊕v）的形式出现，则当中间状态字遍历时，密文字也是平衡的. 借鉴文献[20]给出的构造积分区分器的思想，辅助运用定理1 和定理2，给出了一个构造SPN 结构和Feistel-SP 结构分组密码积分区分器的通用框架. 在介绍通用框架之前，本节先给出构造过程中用到的一些概念.

本步骤关注从中间状态Q开始，经过r轮加密得到Y的加密过程. 把每个密文字yi用中间状态字q0,q1, …,qn−1表示出来，然 后统计每个中间 状态字qj在每个密文字yi表达式中出现的次数. 当加密轮数超过某个数值re时，每个中间状态字qj在每个密文字yi表达式中至少出现1 次，小于数值re时，有些中间状态字在某些密文字表达式中出现次数为0，re即加密方向全扩散的轮数. 假设qa在加密re轮后的密文字yb的表达式中只出现1 次，根据定理1，当qa活跃，其他中间状态字固定为常数时，加密re轮后，密文字yb是平衡的，这样可以得到一个

3 对WARP 算法的积分分析

设计者利用MILP 和可分性，给出了一个需要2124个选择明文（令31 个明文字活跃）的20 轮积分区分器，设计者认为利用该积分区分器最多只能实现21 轮密钥恢复攻击. 本节中利用多变量多项式的代数结构分析方法给出了2 个只需要2116个选择明文（令29 个明文字活跃）的22 轮积分区分器，并且利用该积分区分器，至少可以实现26 轮密钥恢复攻击. 为方便实验验证，本文特地给出了一个时间复杂度为232的18 轮可实现积分区分器.

3.1 构造20 轮积分区分器

根据第2 节给出的框架，分3 步来构造WARP的积分区分器.

步骤1. 构造Te.

假设从中间状态Q=（q0,q1, …,q31）加密r轮后得到密文Y=（y0,y1, …,y31），将每个密文字yi用q0,q1, …,q31表示出来，然后统计中间状态字qj在yi中出现的次数. 具体做法如下所示.

当r=1 时，用中间状态字q0,q1, …,q31把1 轮加密后的密文字y0,y1, …,y31表示出来，请见附录A 中式（A1）.

迭代1 轮加密的表达式，得到r=2, 3, …, 10 轮后每个密文字yi的多变量多项式表达式. 由1 轮加密表达式可以看出，中间状态字qj在r轮密文字yi中出现次数等于qj在某些r−1 轮密文字中出现次数之和，编程迭代计算可以得到每个中间状态字在每个r轮密文字中出现的次数. 我们发现10 轮时达到了全扩散，即每个qj在每个yi的表达式中至少出现1 次，如图2所示. 图2 中的（i,j）元素表示第j个中间状态字在第i个密文字中出现的次数. 假设qu在yv的表达式中恰好出现1 次，则令qu活跃，其他中间状态字固定为常数，加密10 轮之后的密文字yv是平衡的.

接下来，本文借助于实验寻找加密更多轮后积分为0 的密文字. 依次令单个中间状态字qj活跃，其余的31 个中间状态字固定，观察加密多于10 轮后是否仍存在积分为0 的密文字. 实验发现加密11 轮和12 轮后依然存在积分为0 的密文字，但这些密文字是否真正平衡需要根据定理1 和定理2 对该密文字表达式的代数结构进行判断. 例如，令q3活跃，其他中间状态字固定，加密12 轮之后的密文字y15的积分为0.q3在y15表达式中出现4 次，写出y15的代数表达式（详见附录B），发现该表达式结构为：y15=S（S（x⊕α）⊕S（x）⊕β）⊕$（q3）⊕$′（q3）⊕γ，其 中α，β，γ是不包含q3的项，$（q3）和$′（q3）是定理1 中所示S 盒的复合，q3在其中各出现1 次. 当q3活跃，其他中间状态字为常数时，根据定理1 和定理2，y15平衡. 从而可以得到一个同样的方法，可以得到另一个另外还有若干个11 轮的Traile.

Fig.2 The number of times qj appears in yi after 10-round encryption图2 加密10 轮后qj 在yi 的表达式中出现的次数

步骤2. 构造Td.

假设从中间状态Q开始解密r轮得到明文X=（x0,x1, …,x31），用q0,q1, …,q31把每个明文字xi表示出来，并统计qj在每个xi的表达式中出现的次数.

当r=1 时，用中间状态字q0,q1, …,q31把一轮解密后的明文字x0,x1, …,x31表示出来，请见附录A 中式（A2）.

迭代一轮解密的表达式，得到r=2, 3, …, 10 轮解密后的每个明文字xi的表达式，并统计每个中间状态字qj在其中出现的次数，发现与加密相同，解密10 轮时达到了全扩散. 解密9 轮时，存在qj在某些xi的表达式中出现次数为0，例如，q0在x16，x26，x28的表达式中出现次数为0，从而可以得到一个本文中 令A={x0,x1, …,x31}，xi∈{0,1}4. 通过解密9 轮后qj在xi的表达式中出现的次数，如图3所示，可以找到所有从而得到二元关系图3 中的（i,j）元素表示第j个中间状态字在第i个明文字中出现的次数.

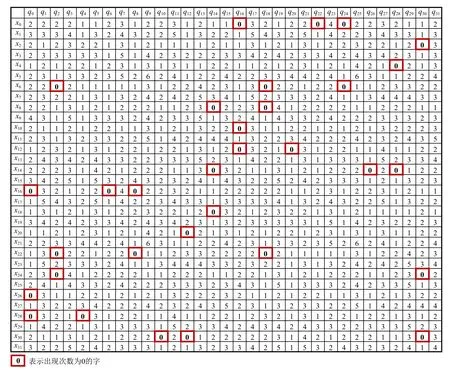
Fig.3 The number of times qj appears in xi after 9-round decryption图3 解密9 轮后qj 在xi 的表达式中出现的次数

20 轮积分区分器Ⅰ: 令集合{xi|i∈{0, 1, …, 31}{8, 14, 18}}中的每 个明文字活跃，x8，x14，x18为常数，经过20 轮加密后，y15是平衡的.

20 轮积分区分器Ⅱ：令集合{xi|i∈{0, 1, …, 31}{2, 24, 30}}中的每 个明文字活跃，x2，x24，x30为常数，经过20 轮加密后，y31是平衡的.

2 个积分区分器的数据复杂度都是229×4=2116个选择明文，低于设计者给出的积分区分器的复杂度231×4=2124个选择明文.

3.2 扩展为22 轮积分区分器

Feistel 结构轮函数具有如下特点，有一半状态没有变化，直接赋值给下一轮的状态比特，同时这半数状态经过轮函数后和剩下的另一半状态异或后赋值给下一轮的另一半状态. 通过观察WARP 轮函数的加解密代数表达式发现，每个中间状态字都可以被它的前一轮或者后一轮的2 个状态字、密钥字和轮常数表示出来. 特别是，轮密钥的异或发生在S 盒之后. 利用这一特性，可以将3.1 节所得20 轮积分区分器向解密方向和加密方向各扩展1 轮，得到22 轮积分区分器.

以20 轮积分区分器Ⅰ为例，该区分器由Td9中的有序对〈A{x8,x14,x18},q14〉与中的有序对连接而成. 我们将其置于22 轮积分区分器的第1～21轮的位置，q14为第10 轮的中间状态字如图4 所示.

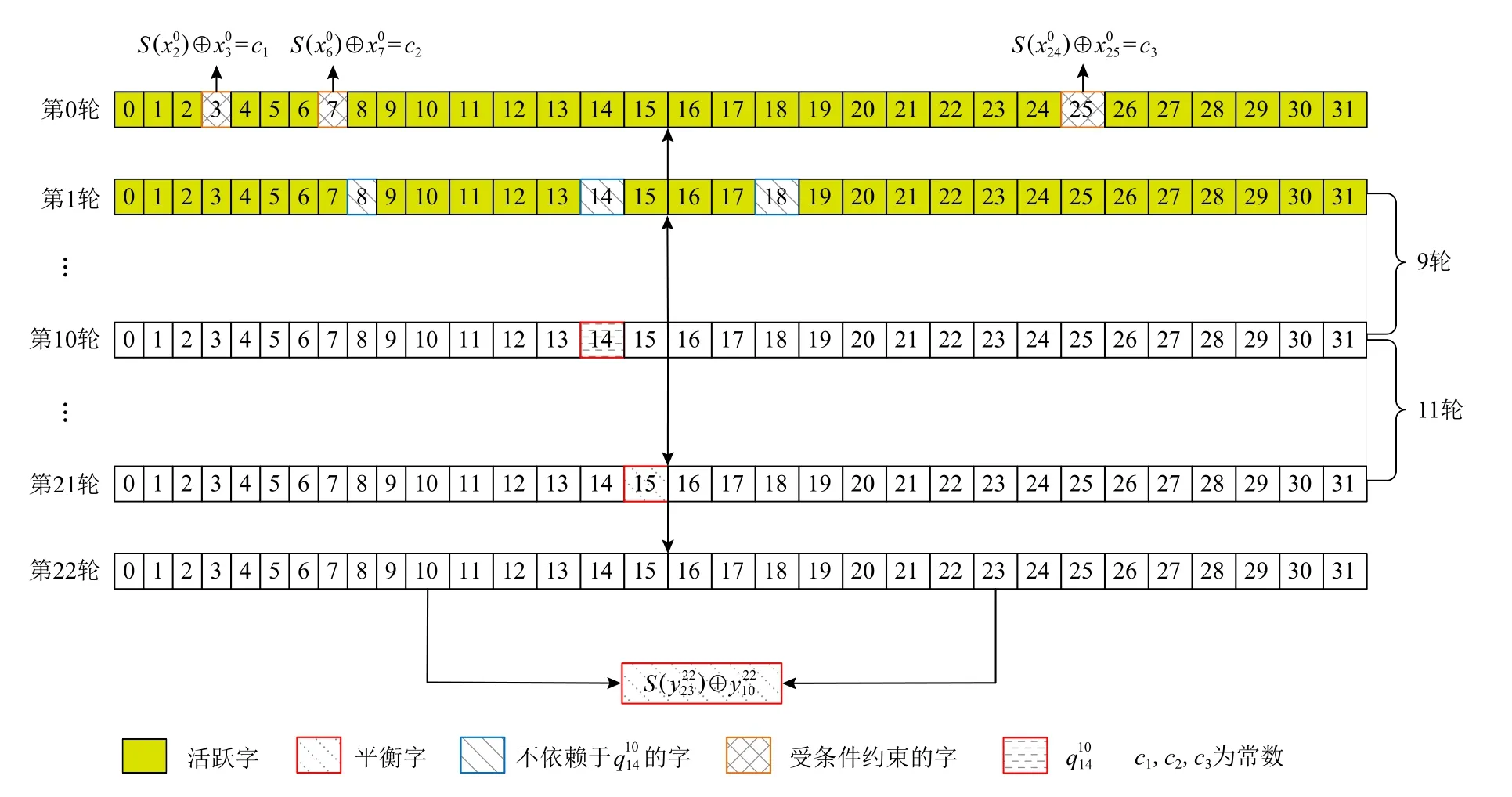
Fig.4 A 22-round integral distinguisher图4 22 轮积分区分器

2 个22 轮积分区分器的数据复杂度仍然是 2116个选择明文.

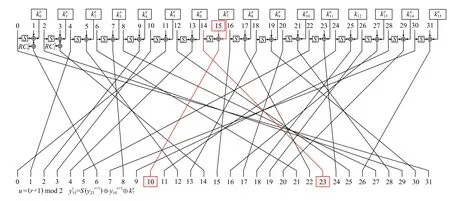
Fig.5 The balanced combinations of ciphertext图5 平衡的密文字组合

3.3 构造18 轮可实验验证的积分区分器

当减少构造区分器的Traild的轮数时，区分器所需的活跃明文字个数也会减少. 用一个和一个通过q14连接，构造了一个16 轮积分区分器：令{x0,x1, …,x31}中的{x5,x14,x15,x18,x19,x20,x21,x27}明文字活跃，其余的明文字为常数，加密16 轮后，y15平衡.然后将此区分器分别在解密方向和加密方向各扩展1 轮，得到一个18 轮积分区分器，即：令明文字x3,x6,x8,x16,x22,x25,x26,x29活 跃，令x7⊕S（x6）,x9⊕S（x8）,x17⊕S（x16）,x23⊕S（x22）,x27⊕S（x26）,x0,x1,x2,x4,x5,x10,x11,x12,x13,x14,x15,x18,x19,x20,x21,x24,x28,x30,x31为常数，加密18 轮后，S（y23）⊕y10平衡. 该区分器的数据复杂度为28×4=232个选择明文，随后在配置为Intel Xeon E5-2670 v2 @2.5 GHz, 2.49 GHz，16.00 GB RAM 的 服务器上进行了实验，运行时间为7.1 h，证实了结论的正确性.

3.4 对WARP 算法的26 轮积分攻击

基于22 轮积分区分器，利用部分和技巧[2,23]在区分器尾部加4 轮，对26 轮WARP 进行了密钥恢复攻击.

2 个表达式中包含13 个26 轮密文字和10 个轮密钥字.

攻击步骤有3 步：

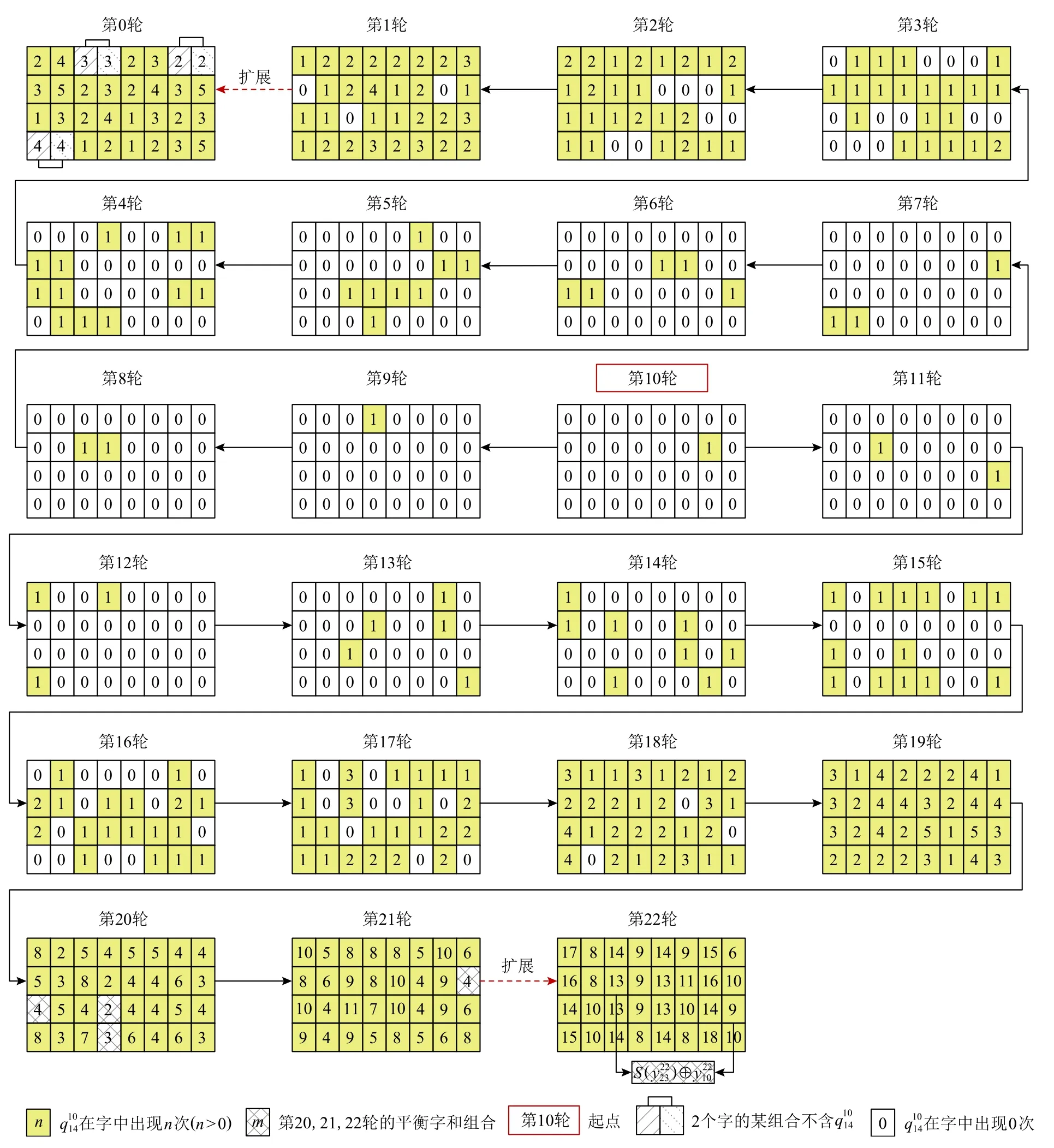
Fig.6 The trail of the dependence on in the 22-round distinguisher图6 22 轮区分器中对的依赖关系迹

在3.3 节给出的18 轮区分器尾部加1 轮，对19轮WARP 进行可实现的密钥恢复攻击，可以恢复4b密钥本文在同一个服务器上进行了实验，运行时间约为7.6 h，验证了该攻击方法的正确性.

4 总结

本文将明密文字用中间状态字的多变量多项式来表示，通过对多变量多项式进行分析，发现了一类代数结构具有的积分特性，用该性质改进了SPN 和Feistel-SP 分组密码积分分析的结果. 将该方法应用于WARP 算法，分析轮数由原来设计者给出的21 轮提高到26 轮. 据我们所知，该区分器和密钥恢复攻击是迄今为止单密钥情境下最好的结果.

附录A.

附录B.

作者贡献声明：邢朝辉负责分析方法的理论分析、实验设计及实现、论文撰写；张文英提出分析思路、指导写作并修改论文；曹梅春负责图表整理及论文校对.