类型增强的时态知识图谱表示学习模型

何 鹏 周 刚 陈 静 章梦礼 宁原隆

1 （战略支援部队信息工程大学 郑州 450001）2 （郑州工程技术学院 郑州 450044）

（helen830209@163.com）

知识图谱（knowledge graph）以多关系有向图的形式组织和存储现实世界的知识. 其中，节点表示实体（人名、地名、机构名、概念等），边表示实体间的语义关系. 因此，知识图谱又可以看成是结构化三元组的集合，对应有向图中的边（关系）及其相连的2个节点（实体）. 自从2012 年，谷歌首次提出知识图谱的概念并将其成功应用于信息检索领域以来，知识图谱在学术界和工业界得到了广泛的关注和研究.现有的知识图谱包括Freebase[1]、Dbpedia[2]、WordNet[3]等，已经在许多人工智能相关的应用中起到了巨大的推动和支撑作用，如个性化推荐[4]、智能问答[5]、信息检索[6]以及自然语言处理[7]等.

现有的知识图谱规模庞大，往往包含上亿条事实三元组，不可避免的存在由数据缺失造成的不完整性问题. 为了解决此问题，人们提出了各种知识图谱补全方法，通过基于已有的事实来推理和预测知识图谱中缺失的链接. 知识图谱表示学习（knowledge graph representation learning）是一种有效的知识图谱补全方法，它可以自动预测缺失的知识，同时解决知识图谱中的数据稀疏性和计算效率问题，为基于知识图谱的深度学习工作提供了极大的便利.

知识图谱表示学习又称为知识图谱嵌入（knowledge graph embedding），旨在将知识图谱中的元素（实体和关系）映射到低维的连续向量空间中，学习实体和关系的嵌入表示，同时保持知识图谱的内在结构和语义信息，即将知识图谱的符号化表示形式转换成数值化表示形式，从而实现高效的语义计算. 现有的知识图谱表示学习模型通常是静态的，忽略了事实的时间动态性和时序依赖性. 而在现实世界中，时间是实体和关系所具有的重要属性，事实往往随时间的变化而发生动态的演化. 常见的知识图谱Wikidata[8]和YAGO[9]都包含了知识的时间信息. ICEWS[10]和GDELT[11]是2 个带有时间信息的事件知识图谱. 将知识图谱中可提供的时间信息引入三元组中，构成的带有时间戳的四元组集合称为时态知识图谱（temporal knowledge graph）. 如图1 所示，连接实体的关系带有时间戳，表明该事实发生的具体时间，比如（美国，总统，奥巴马， [2009—2017]）只在2009—2017 年间有效. 当采用静态的知识图谱表示学习模型对时态知识图谱进行补全时，很容易混淆相似实体的语义信息. 比如，当对缺失实体的事实（美国，总统，？，[1993—2001]）进行链接预测时，如果忽略了给定的时间戳[1993—2001]，则可能会混淆“克林顿”和其他历届美国总统，给出错误的答案. 时态知识图谱表示学习模型通过将可提供的时间信息显式或隐式的融合到知识图谱表示学习过程中，使得链接预测的结果随时间不同而产生不同的排序，从而有效地区分相似语义的实体，提高时态知识图谱补全的准确性.

Fig.1 An example of temporal knowledge subgraph extracted from the Wikidata图1 从Wikidata 抽取的时态知识图谱子图示例

由于上述优点，最近几年时态知识图谱表示学习迅速成为知识图谱领域的研究热点. 已经有一些时态知识图谱表示学习模型通过利用时间信息来改善表示学习的效果，但它们普遍存在一个或多个问题：1）不具备完全表达性，即不能准确的区分事实（比如，“2009—2017 年间的美国总统是奥巴马”）与非事实（如“2009—2017 年间的美国总统是希拉里”）[12]，从而限制了模型的表示能力. 2）只考虑时间点形式的时间戳（如[2014-07-16]），而没有考虑时间段形式的时间戳（如[2009—2017]）. 比如，在Wikidata 和YAGO这2 个著名的时态知识图谱中，事实通常带有时间段形式的时间戳，由于时间的连续性，建模时间段形式的时间戳是一项具有挑战性的工作. 3）存在冗余计算和时空复杂度高的问题. 4）没有充分利用类型兼容性. 类型兼容性是指知识图谱中的实体除了表示个体语义信息外，还隐含了一般的类型语义信息，且一个特定关系总是连接具有相同类型的实体. 比如（美国，总统，？）中，“总统”这一关系总是连接“国家”类型和“人”类型的实体. 在推理缺失信息时，利用类型兼容性这一先验知识可以判断缺失实体的类型应该是“人”，它在向量空间中应该与其他“人”类型的实体位置接近，从而可以更好地限制和优化实体嵌入.

为了解决这些问题，本文提出一种类型增强的时态知识图谱表示学习模型（type-enhanced temporal knowledge graph representation learning model, T-Temp），用于解决时态知识图谱中的知识补全和语义计算问题. 模型基于张量分解技术，将时态知识图谱看成3 阶张量，语义关系和时间信息联合索引其中的一个模式向量. 同时，设计一种类型兼容性函数，自动捕获实体的类型特征并优化实体表示. 此外，模型具有完全表达性，且可以建模时态知识图谱中常见的时间点形式和时间段形式的时间信息，具有普遍适用性.

本文的主要贡献包括3 个方面:

1）提出了一种基于张量分解的时态知识图谱表示学习模型T-Temp，将时间信息显式地编码到表示学习过程中，并利用实体和关系的类型兼容性，学习实体、关系、时间和类型的嵌入表示，提升表示学习的有效性.

2）理论上证明T-Temp 模型具有完全表达性，并与现有的同类模型做对比分析，说明其具有较低的时间和空间复杂度.

3）在真实的时态知识图谱ICEWS、Wikidata、YAGO 中抽取出来的4 个公开数据集上开展广泛的实验. 在链接预测任务上的结果表明T-Temp 模型的性能较其他先进模型有显著提升，类型嵌入的可视化聚簇结果也表明T-Temp 模型能够有效地捕获实体的类型特征.

1 相关工作

本节主要介绍与本文工作相关的知识图谱表示学习模型，包括静态知识图谱表示学习模型、时态知识图谱表示学习模型和类型增强的知识图谱表示学习模型，具体可参考综述文献[13−16].

1.1 静态知识图谱表示学习模型

现有的大多数知识图谱表示学习模型基于静态事实进行建模，大体上可分为2 类：基于平移距离的模型和基于张量分解的模型.

基于平移距离的模型通常将关系建模成向量空间中的平移或旋转操作，用关系操作后的实体间距离度量事实的真实性. 著名的基于平移距离的模型TransE[17]及其变体模型TransH[18]、TransR[19]、TransD[20]等均将关系建模为实数向量空间中的平移操作. 而最近的RotatE[21]和HAKE[22]模型则将关系建模为复数向量空间中的旋转操作，从而推理知识图谱中的各种关系模式，提高模型的关系建模能力. 然而，大部分平移距离模型不具备完全表达性[12]，限制了其表示能力，基于张量分解的SimplE[12]模型能够克服这一缺点. SimplE 模型受到经典张量分解技术——典 范多元（CANDECOMP/PARAFAC, CP）分 解[23]——的启发，将每个事实三元组对应3 阶张量中的1 个元素，其中，实体和关系分别索引该张量的一个模式向量，同时构建反向关系来统一不同位置的实体嵌入.Lacroix 等人[24]也提出了类似的基于CP 分解的模型.ComplEx[25]模型是另一个基于张量分解的模型，它通过将实体映射到复数向量空间而非实数向量来建模实体间的关系. ComplEx 和SimplE 都具有完全表达性[12,24]，但与SimplE 相比，ComplEx 存在冗余计算问题. 此外，Yang 等人[26]提出一个简化版的张量分解模型DistMult，王培妍等人[27]提出一种基于张量分解的知识超图模型Typer.

尽管静态知识图谱表示学习模型取得了较好的表现，但它们没有考虑知识的时态演化性，容易造成相似语义实体的混淆.

1.2 时态知识图谱表示学习模型

最近，一些研究者通过对静态模型进行时态扩展，提出了时态知识图谱表示学习模型. 比如，TTransE[28]、TA-TransE[29]、HyTE[30]、Duration-HyTE[31]模型是对经典静态模型TransE 的时态扩展，和TransE 一样，这些动态模型不具备完全表达性. 受到静态模型RotatE的启发，TeRo[32]模型将时间信息建模成复数空间中的旋转操作，实体通过沿不同角度的时间旋转来体现不同时期的时间特征. ChronoR[33]模型同样受到静态模型RotatE 的启发，但实体的旋转变换由时间和关系共同决定，且采用向量间的角度而非距离来度量事实的真实性. DE-SimplE[34]模型在静态模型SimplE的基础上，通过引入DE（diachronic embedding）函数[35]来学习实体的时间演化特性. ConT[36]模型可以看成是静态模型Tucker[37]的扩展，它用特定时间张量代替Tucker 分解[38]中的核张量. 由于其时间嵌入需要大量的参数，在训练过程中效率较低且容易产生过拟合. ChronoR、DE-SimplE、ConT 模型都只能处理离散的时间点信息，而没有考虑连续的时间段信息.TComplEx 和TNTComplEx[39]模型将时态知识图谱表示成一个4 阶张量，并添加一个时态模式向量来扩展静态模型ComplEx. 同样，TComplEx 和TNTComplEx模型也存在冗余计算问题.

1.3 类型增强的知识图谱表示学习模型

实体的类型特征体现了实体的一般语义和类别，相关工作利用这一特征进一步优化知识表示的学习效果. TKRL[40]模型首次引入显式的实体类型来增强TransE. JOIE[41]模型将知识图谱表示为本体视图（即类型信息）和实例视图（即实体信息），并联合编码这2 个视图. TaRP[42]模型根据实体类型定义关系类型，并采用贝叶斯规则拟合关系类型和实体类型间的语义相似性. 上述模型均需要提供额外的类型信息. 最近，Jain 等人[43]认为实体类型普遍隐含在知识图谱中的实体和实体间的复杂语义关系中，并提出TypeDM和TypeComplEx 模型，通过建模实体和关系间的类型兼容性扩展DistMult 和ComplEx 模型，自动学习实体的类型嵌入，不需要额外的类型信息. 然而，所有这些类型增强模型都没有考虑知识的时间动态性.

与上述工作相比，本文工作主要致力于解决时态知识图谱中的知识补全问题. 本文提出的类型增强的时态知识图谱表示学习模型T-Temp 属于张量分解模型. 在表示学习过程中，T-Temp 模型可以以较低的时空消耗，充分利用各种形式的时间信息，并自动学习和表示实体的类型特征，不需要提供额外的类型信息. 此外，据我们所知，T-Temp 模型是为数不多的具有完全表达性的时态模型.

2 类型增强的时态模型T-Temp

本节首先对时态知识图谱表示学习中的相关问题进行形式化定义，并对一些基本的概念和符号进行解释；然后详细介绍所提出的T-Temp 模型.

2.1 问题定义

定义1.时态知识图谱. 时态知识图谱表示成一个带有时间信息的多关系有向图G=(E,R,T)，其中E是节点（实体）集，R是边（关系）集，T是时间戳集. 因此，时态知识图谱又可以看成是四元组(h,r,t,τ)∈G或(h,r,t,[τs,τe])∈G的集合，其中h,t∈E分别称为头实体和尾实体，r∈R是它们之间的关系，τ ∈T或[τs,τe]∈T是与事实相关联的时间戳. 具体来说，τ表示事实发生在一个特定的时间点，[τs,τe]表示事实在一个开始时间为 τs、结束时间为 τe的持续时间段内均有效.

定义2.时态知识图谱存在不完整性问题. 本文用W⊂E×R×E×T表示现实世界中的全部事实，时态知识图谱G是W的子集（即G⊂W），时态知识图谱补全是一个根据G推理W的问题.

定义3.知识图谱表示学习模型通常定义3 件事：

1）嵌入函数——将知识图谱中的元素映射为向量、矩阵或张量等嵌入表示；

2）得分函数——将上述嵌入表示作为输入，通过数值运算获得输出，作为评估事实真实性的得分；

3）损失函数——通过最大化所有已知事实的得分来学习和优化各元素的嵌入表示.

2.2 T-Temp 模型整体架构

本文基于张量分解的模型，学习实体、关系和时间戳的向量化嵌入. 同时，利用实体和关系的类型兼容性，自动学习实体的类型嵌入，进一步优化实体表示. 图2 展示了模型的整体架构，按照知识图谱表示学习的过程，首先，我们提出将已知四元组嵌入到实数向量空间中的嵌入函数；接着，定义基于CP 分解的得分函数以及基于语义相似性的类型兼容性函数，并将两者结合，形成最终的得分函数；最后，设计一个带有正则化的交叉熵损失函数作为优化目标，学习各元素的嵌入表示.

2.3 嵌入函数

嵌入函数又称为编码器. 本文将时态知识图谱中的实体、关系和时间戳元素显式的编码到维度为d的实数向量空间. 如图2 所示，对于给定四元组(h,r,t,τ)，向量h,t∈Rd分别是头实体h和尾实体t经过嵌入函数映射后得到的嵌入表示，代表头/尾实体的个体语义特征，向量分别是关系r和时间戳 τ经过嵌入函数映射后得到的嵌入表示，代表关系和时间戳的语义特征，其中rd+τd=d.

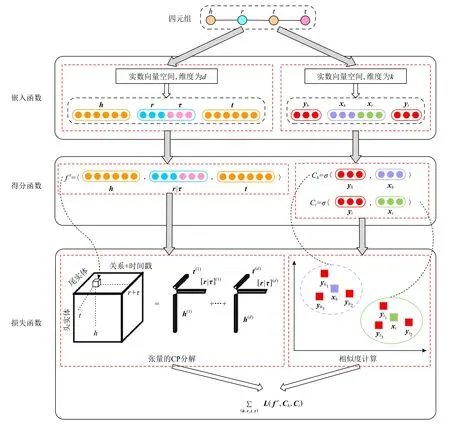
Fig.2 T-Temp architecture图2 T-Temp 架构

为了学习实体所隐含的类型特征并建模实体与关系间的类型兼容性，嵌入函数进一步将实体所属的类型信息编码到维度为k的实数向量空间中. 具体来说，向量yh,yt∈Rk分别表示头实体h和尾实体t的类型嵌入，代表头/尾实体的类型特征. 此外，构建关系的类型属性，根据一个特定关系总是连接具有相同类型的头实体和尾实体，令关系r期望连接的头实体类型为关系的头类型，关系r期望连接的尾实体类型为关系的尾类型. 并定义向量xh∈Rk为关系r的头类型嵌入，表示关系的头类型特征；向量xt∈Rk为关系r的尾类型嵌入，表示关系的尾类型特征. 实体类型体现了多个实体的一般语义信息，往往没有实体的语义丰富，因此通常情况下k≪d.

2.4 得分函数

本文定义基于CP 分解的得分函数，将时态知识图谱G看成一个3 阶张量X∈R|E|×|R||T|×|E|，其中 |E|是实体的个数，|R||T|是关系个数 |R|和时间戳个数 |T|的乘积. 头/尾实体分别索引模式-1 和模式-3 向量，关系和时间戳联合索引模式-2 向量. 根据定义4 所描述的CP 分解方法，头实体向量、尾实体向量、关系向量和时间戳向量组成的多线性乘积可以用来估计张量X中的各个元素，即四元组(h,r,t,τ)的得分函数为

其中h表示头实体向量，t表示尾实体向量，[r|τ]表示关系向量r和时间戳向量 τ的级联. 该得分函数的值越大，说明四元组越真实. 需要指出的是，这种原始的基于CP 分解的方法存在同一实体位于头/尾不同位置时的嵌入向量不一致问题，为了解决这个问题，本文在训练时采用与静态模型SimplE 类似的，构建反向关系的方法统一实体的嵌入.

另一方面，考虑到本文所提出的模型不需要提供额外的类型信息，实体和关系的语义关联中其实隐含了它们的类型特征. 为了可以自动学习和挖掘这些类型特征，根据实体和关系的类型兼容性这一先验知识，我们定义基于语义相似度的类型兼容性函数来建模实体和关系间的类型兼容性，采用与余弦相似度的计算成比例的向量内积形式. 对于关系与其相连的头实体，类型兼容性函数为

其中yh表示头实体的类型向量，xh表示关系r期望连接的头类型向量，σ是sigmoid 函数. 类似地，对于关系与其相连的尾实体，类型兼容性函数为

其中yt表示尾实体的类型向量，xt表示关系r期望连接的尾类型向量.(h,r,t,τ)

将式（3）与式（4）（5）相结合，得到四元组的最终得分函数：

式（6）中2 个类型兼容性函数可以看成是CP 分解得分函数的系数，即根据四元组的类型兼容性调节该得分函数的结果.

除此之外，常见的时态知识图谱通常是异构的，也就是说，除了时态感知关系，还包含大量的非时态感知关系. 比如Wikidata 中的三元组（奥巴马，出生地，夏威夷州），其关系“出生地”就是一个非时态感知关系，即奥巴马的出生地永远是夏威夷州，不会随时间发生变化. 为了能更好地处理这种既包含时态关系，又包含非时态关系的异构型时态知识图谱，本文在得分函数中增加了一个非时态组件，相应的得分函数变为

其中rs∈Rd表示关系r的非时态向量，而r又称为关系的时态向量表示. 对于时态感知关系来说，由于其通常出现在含有时间信息的四元组中，因此，该关系对应的时态向量r应该使正四元组得分较高，负四元组得分较低；而其对应的非时态向量rs应该使大部分不含有时间信息的三元组得分较低. 相反，对于非时态感知关系来说，其对应的非时态向量rs应该使正三元组得分较高，负三元组得分较低；而其对应的时态向量r应该使大部分含有时间信息的四元组得分较低.

2.5 损失函数与时间戳预处理

在2.4 节定义的得分函数基础上，对于缺失尾实体的四元组(h,r,?,τ)，我们可以估计任意候选实体ti∈E的真实性：

对于缺失头实体的四元组(?,r,t,τ)也类似. 进而，本文采用交叉熵损失函数来学习和优化各元素的向量化嵌入：

此外，考虑到参数正则化可以提升模型的泛化能力，避免对训练数据的过拟合，本文采用类似于文献[37]中的张量核范数Ωp(θ)和基于先验知识的时间戳平滑 ∆p作为模型的正则化项：

其中||·||p表示向量的p-范数，τi和τi+1表示任意2 个相邻的时间戳嵌入表示. 模型的最终优化目标是最小化带有正则化项的损失函数：

其中λ1和 λ2是加权超参.

在模型进行训练之前，需要考虑如何处理时态知识图谱中常见的2 种时间信息形式，即时间点时间戳和时间段时间戳. 在事件知识图谱ICEWS 和GDELT 中，事实（事件）带有时间点形式的时间戳 τ，用来表示该事件发生的具体时间. 由于时间点的离散性特点，这种形式的时间信息可以直接适用于TTemp 模 型. 而 在时态知识图谱YAGO 和Wikidata 中，与事实相关联的往往是时间段形式的时间戳[τs,τe]，如何建模这种连续性时间信息是一项具有挑战性的任务. 与TComplEx 和TNTComplEx 模型中 采用的 在时间段范围内均匀采样的方法不同，我们直接用时间段的开始时间和结束时间作为新的时间戳来代替原有的时间戳，从而将持续性时间信息做离散化处理. 本质上是利用扩充数据量的方法尽可能多地采集连续性时间信息，形成模型可处理的四元组形式.算法1 给出了T-Temp 模型的伪代码.

算法1.T-Temp 模型.

输入：训练集Strain，实体集E，关系集R，时间戳集T，训练总轮数N，批次大小 β，嵌入维度k，d和rd，τd，加权超参 λ1和 λ2；

输出：所有实体的嵌入向量e∈{h,t}和类型嵌入向量ye，所有关系的嵌入向量r，rs和头/尾类型嵌入向量xe，所有时间戳的嵌入向量 τ.

2.6 完全表达性证明

完全表达性是知识图谱表示学习模型的一个重要属性，现有工作[12,34,38]已经证明，基于张量分解的静态模型ComplEx、SimplE、Tucker 具有完全表达性，最近提出的DE-SimplE 模型是第1 个具有完全表达性的时态模型. 本文从理论上分析T-Temp 模型的完全表达性.

定义5.知识图谱表示学习模型具有完全表达性，当且仅当给定知识图谱中的已知事实（真事实）集合，存在一种嵌入表示，能够正确区分真事实与假事实.

Kruskal[44]将N阶张量的秩定义为能够进行CP分解的最小R值. 虽然确定给定张量的秩是个NP 难问题[45]，但Kruskal[46]已经证明3 阶张量的秩存在一个弱上界. 受到此证明启发，本文证明T-Temp 模型具有完全表达性，并给出嵌入表示的边界.

定理1.给定实体集E、关系集R和时间戳集T上的已知事实集合G，存在维度为|E|×|R|×|T|的嵌入表示，使得T-Temp 模型具有完全表达性.

证明. T-Temp 模型具备完全表达性的充分条件是，真事实和假事实的得分永不相交，即得分函数能够正确划分所有真事实与假事实. 由于得分函数中的Ch和Ct取值位于0～1 之间，不影响总体函数值的正负，为了简化证明，我们只关注得分函数的第1 部分f′.

大小为|E|×|R|×|T|的嵌入向量可以看成是 |E|个大小为|R|×|T|的块. 对于头实体ei，令其嵌入向量ei∈R|E|×|R|×|T|第i块中的所有元素值为1，其余块中的元素值均为0. 于是，只有第i块中的元素值对四元组(ei,rk,ej,tl)的得分有影响. 接下来，进一步分析嵌入向量的第i块.

在大小为|R|×|T|的第i块中，令关系rk和时间戳tl的嵌入向量级联[rk|tl]∈R|E|×|R|×|T|的第i块第(k×|T|+l)个元素值为1，其余为0. 因此，嵌入向量ei与[rk|tl]的哈达玛积中，只有第i块第(k×|T|+l)个元素为1，其余为0. 基于以上嵌入向量的元素值设置，如果四元组(ei,rk,ej,tl)为真事实，只需要令尾实体嵌入向量ej∈R|E|×|R|×|T|的第i块第(k×|T|+l)个元素值为1，否则值为−1，即可得到真事实的得分〈ei,[rk|tl],ej〉为1，假事实为−1，互不相交. 证毕.

2.7 时间和空间复杂度分析

时间和空间复杂度是知识图谱表示学习模型的另一个重要属性，会直接影响模型的训练效率和可扩展性. 如表1 所示，本文根据嵌入函数和得分函数分析比较T-Temp 模型和几个现有的时态模型所需的参数量和时间消耗，其中 γ为调整时态特征权重的超参[34]. 在时间复杂度方面，除ConT 模型外，所有模型都消耗与嵌入维度呈线性的时间复杂度O(d). 由于ConT 模型涉及3 阶张量运算，其时间复杂度为O(d3).在参数个数方面，除了DE-SimplE 模型，其他模型的参数个数均与时间戳的个数相关. 由于本文所提出的T-Temp 模型可以自动学习类型特征，模型需要与类型表示相关的参数量k(2|E|+4|R|). 而通常情况下k≪d（比如第3 节实验中，d=2000,k=20），因此该部分参数量可忽略不计. 又因为rd+τd=d，所以TTemp 模型所需的参数个数总体上与最先进的ChronoR，TeRo，TNTComplEx 等模型相当甚至更少.

3 实 验

链接预测是标准的知识图谱补全任务，本节通过时态知识图谱上的链接预测任务对T-Temp 模型进行有效性验证. 首先对实验中所采用的数据集、评价指标和基线模型等进行说明. 然后将实验分为5 组以达到不同的实验目的：

1）在4 个通用的数据集上对T-Temp 模型进行链接预测实验，并将实验结果与之前的先进模型进行对比分析，以评估T-Temp 模型的有效性；

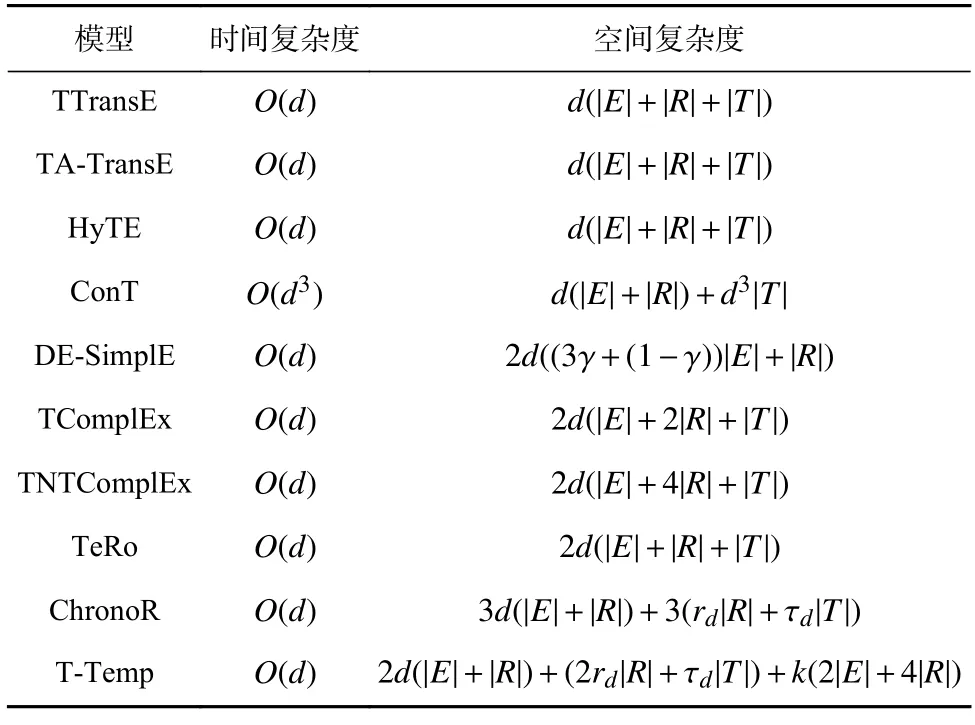
Table 1 Comparison of Our proposed models and State-ofthe-Art Temporal KGE Models on Time Complexity and Space Complexity表1 本文模型与现有时态知识图谱表示学习模型的时间复杂度和空间复杂度对比

2）通过消融实验分析类型兼容性和时间段时间戳的处理方法对T-Temp 模型性能的影响；

3）对学习到的实体和类型嵌入进行聚簇实验，并将聚簇结果进行可视化展示，以验证T-Temp 模型能够自动捕获实体的类型特征.

4）进行超参的敏感性分析实验，以验证模型的性能对于超参设置的敏感度.

5）链接预测任务上的案例研究实验，更细粒度地展示T-Temp 模型如何提升链接预测结果的准确性.

3.1 数据集

本文在4 个抽取自真实时态知识图谱的公开数据集上对T-Temp 模型进行评估，包括：ICEWS14[29]、ICEWS05-15[29]、YAGO11k[30]、Wikidata12k[30].其中，ICEWS14 和ICEWS05-15是Garcia-Duran 等人[29]从事件知识图谱ICEWS中抽取的2个子集. ICEWS包含从1995—2015年发生的政治事件，通过头/尾实体（比如“国家”“总统”）和相连关系（比如“进行访问”“表达会面或谈判的意图”）以及时间点形式的时间戳（如[2014-05-23]）来表示. ICEWS14 和ICEWS05-15 分别对应2005—2015年间发生的政治事件. YAGO11k和Wikidata12k 是时态知识图谱YAGO和Wikidata 的子集，与事实相关联的是时间段形式的时间戳（如[2006-11-18], [2012-08-20]）. 通过YAGO11k 和Wikidata-12k 数据集，可以证明T-Temp 模型能够有效地处理连续性时间信息. 表2 列出了4 个数据集的详细统计信息，需要说明的是，表中YAGO11k 和Wikidata12k数据集的时间戳个数是经过2.5 节中介绍的离散化预处理后的值.

Table 2 Statistics of Datasets表2 数据集的统计信息

3.2 评价指标

为了准确评估模型在链接预测任务上的性能，本文采用2 个广泛使用的评价指标：平均倒数排名MRR（mean reciprocal rank）和击中率Hits@N[21-22,30-34,37].首先，用所有已知实体e∈E分别替换测试集中每个四元组(h,r,t,τ)的头实体h和尾实体t，从而为每个四元组创建2 个候选元组集合(h′,r,t,τ)和(h,r,t′,τ). 然后，用学到的嵌入表示和得分函数为所有候选元组计算得分，并按照得分进行降序排名. 与文献[17]中的设置一样，只对训练集和验证集中均未出现过的候选元组进行排名. 根据此排名，MRR为测试集元组在候选元组集合中排名倒数的平均值：

其中rankh和rankt分别表示测试元组在替换头/尾实体组成的候选元组集合中的排名.Hits@N为排在前N名的测试集元组的平均个数：

其中，C(·)是条件函数，当条件成立时值为1，否则为0.MRR和Hits@N的值越大，说明模型在链接预测任务上的性能越好.

3.3 基线模型和实验设置

本文选取了当前被应用较多的静态和时态知识图谱表示学习模型作为基线模型. 静态模型包括：基于平移距离的TransE 和RotatE 模型，基于CP 分解的DistMult、ComplEx、SimplE 模型；时态模型包括：TransE 的时态扩展模型TTransE、TA-TransE、HyTE.

基于Tucker 分解的时态模型ConT 以及基于CP 分解的时态模型DE-SimplE、TComplEx、TNTComplEx、TeRo、ChronoR. 这些模型均已在第1 节中进行了详细介绍.

为公平起见，本文在单个NVIDIA Geforce RTX 2080Ti GPU 上运行T-Temp 和部分基线模型，使 用Ubuntu 16.04 LTS 操作系统，配置Intel Core i7-7700 3.60GHz CPU，128GB 内存. 本文利用PyTorch[47]实现T-Temp 模型，Adam[48]作为优 化器. 训练批次大小为1 000，训练总轮数为50，且每5 轮验证1 次模型，选择验证集上MRR值最高的模型参数进行测试. 对于ICEWS14 和ICEWS05-15 数据集，最佳参数设置为d=2000，k=20，λ1=λ2=0.01，rd/τd=0.25，学习率为0.2；对于YAGO11k 数据集，最佳参数设置为d=1800，k=30，λ1=0.1，λ2=1，rd/τd=0.6，学习率为0.1；对于Wikidata12k 数据集，最佳参数设置为d=2000，k=30，λ1=λ2=0.01，rd/τd=0.6，学习率为0.1.

鉴于部分基线模型与本文采用的数据集和评价指标相同，直接引用其公开报告的实验结果[32-33]. 对于其他基线模型[36-37]，按照其公开论文中的最佳实验设置进行模型复现.

3.4 链接预测实验

表3 和表4 给出了T-Temp 模型和其他先进模型在4 个数据集上的链接预测结果对比. 总体来说，时态模型在评价指标上优于静态模型，说明在知识图谱表示学习过程中引入时间信息能够显著提升模型性能. 本文提出的T-Temp 模型在所有数据集上的结果均超过最先进的时态模型，表明T-Temp 模型能够有效完成时态知识图谱补全任务.

具体来说，在ICEWS14 和ICEWS05-15 这2 个带有时间点形式时间戳的数据集上，T-Temp 模型的MRR指标结果比最先进的时态模型ChronoR 分别提升了3.9%和1.8%，比同样基于CP 分解的时态模型TNTComplEx 分别提升了8.5%和16%. 这是因为TTemp 模型不仅利用事实的时间信息，还充分挖掘实体的类型特征，从而进一步优化实体嵌入. 而ChronoR和TNTComplEx 模型仅仅融合了时间信息，忽略了隐含在实体关系中的类型信息，因此无法取得更优的结果. 此外，由于ConT 模型中的每个时间戳需要大量参数来表示，容易过拟合，所以ConT 性能欠佳，而且大量参数也使其训练速度尤其缓慢.

YAGO11k 和Wikidata12k 是2 个带有时间段形式时间戳的数据集，ChronoR、DE-SimplE 和ConT 模型不能处理这种连续性时间信息，因此它们在YAGO11k和Wikidata12k 这2 个数据集上没有结果. 尽管TeRo模型采用与本文模型相同的方法来处理持续性时间信息，但T-Temp 模型的结果仍然比TeRo 更优. 一方面是因为TeRo 只考虑通过时间的旋转操作来建模实体的时态演化性，而忽略了关系和整个事实的时间变化属性；另一方面也进一步验证了本文的模型自动挖掘并利用实体类型特征的优点.

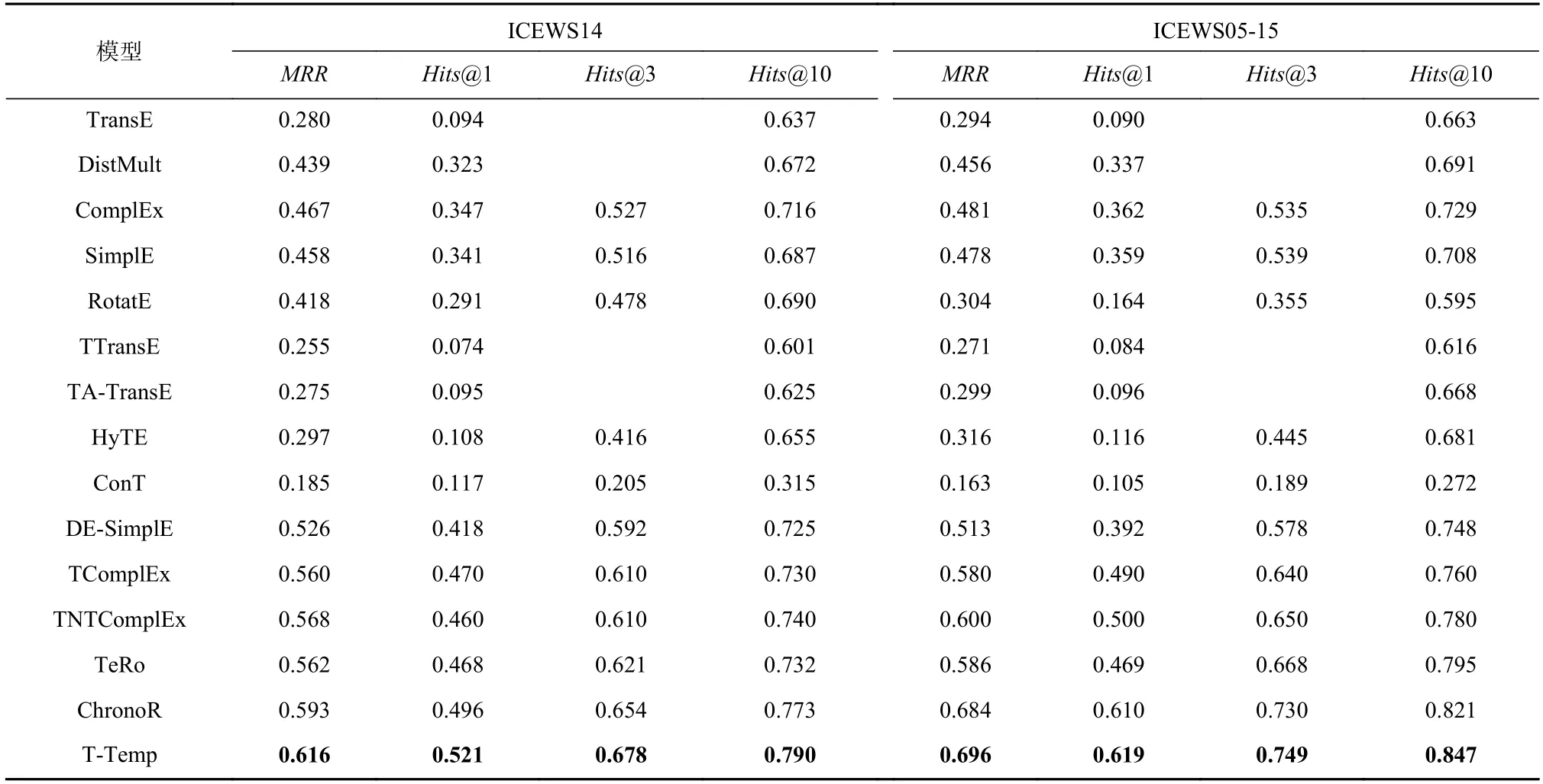
Table 3 Link Prediction Results on ICEWS14 and ICEWS05-15表3 在ICEWS14 和ICEWS05-15 上的链接预测结果

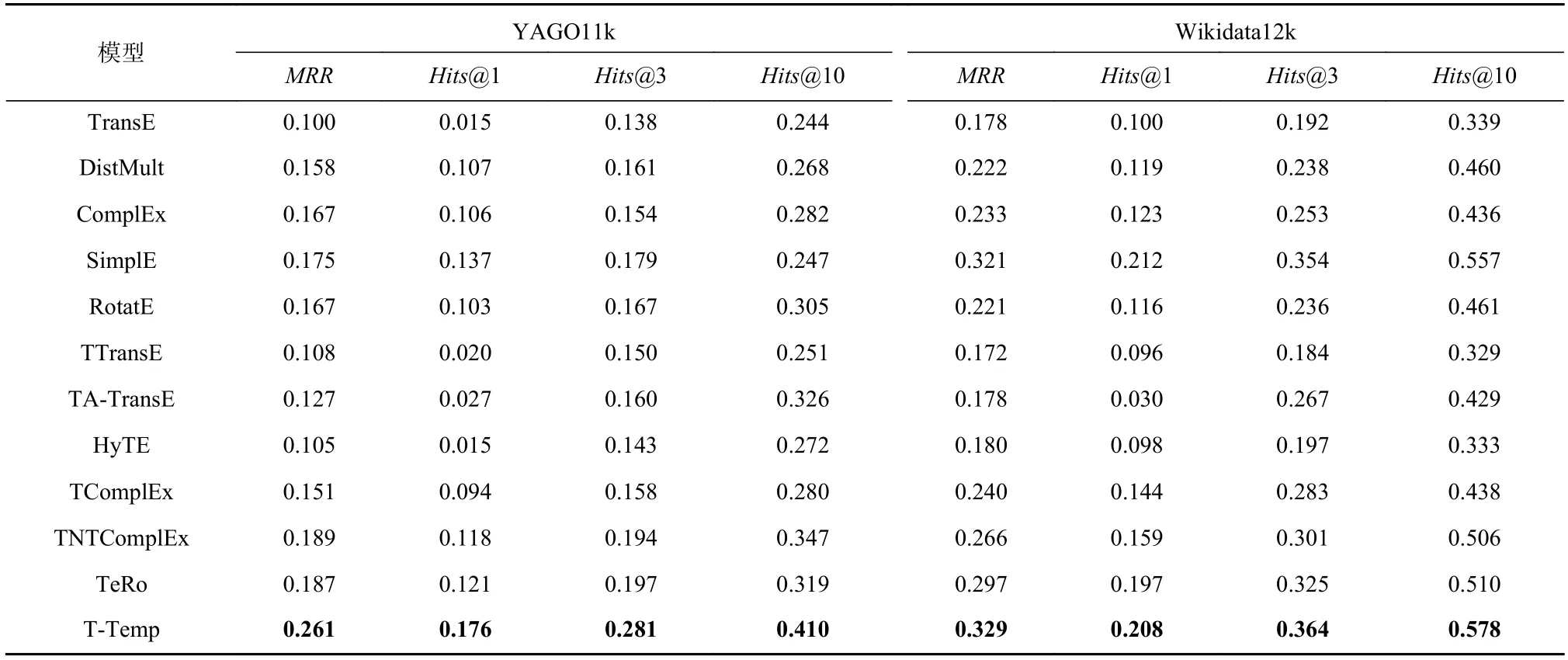
Table 4 Link Prediction Results on YAGO11k and Wikidata12k表4 在YAGO11k 和Wikidata12k 上的链接预测结果

3.5 消融实验

为了分析类型兼容性和连续性时间信息的处理方法对模型性能的影响，本文基于T-Temp 模型设计了2 个变体模型，T-Temp-Type 和T-Temp-Type（Unif），分别表示从T-Temp 的得分函数中移除类型兼容性函数，以及在该变体模型基础上进一步将连续性时间信息的处理方法变为TComplEx 和TNTComplEx模型中采用的均匀采样方法. T-Temp 模型及其变体模型在YAGO11k 数据集上的链接预测结果如表5所示.

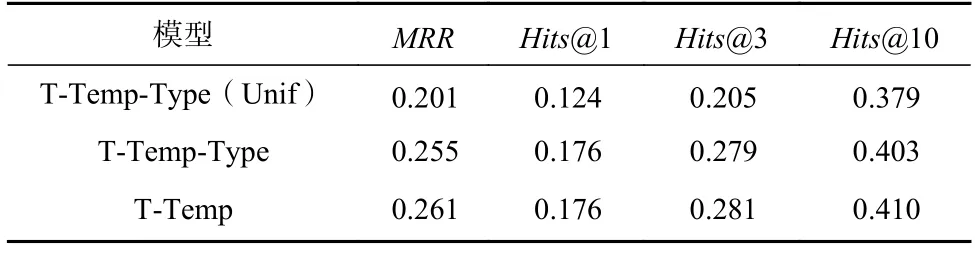
Table 5 Results of Ablation Experiments on YAGO11k表5 YAGO11k 上的消融实验结果

从表5 中可以看出，T-Temp 模型比变体模型TTemp-Type 在MRR评价指标上高2.4%，说明建模类型兼容性并自动学习实体的类型特征确实能提升模型效果. 而变体模型T-Temp-Type（Unif）的结果则进一步退化成与TNTComplEx 相当. 验证了我们设计的连续性时间信息的处理方法可以更多地采集时间的语义信息，有效改进模型性能.

3.6 聚簇和可视化实验

为了评估T-Temp 模型能否有效捕获实体的类型特征，本部分实验对T-Temp 模型在ICEWS14 和YAGO11k 数据集上学习到的实体和类型嵌入进行聚簇，并将聚簇结果可视化. 具体来说，我们采用k-means[49]算法进行聚簇，采用t-SNE[50]方法对实体和类型嵌入进行降维（原来的维度分别是d和k），方便可视化. 图3分别展示了在不同数据集上的聚簇结果，不同的簇用不同颜色标识.

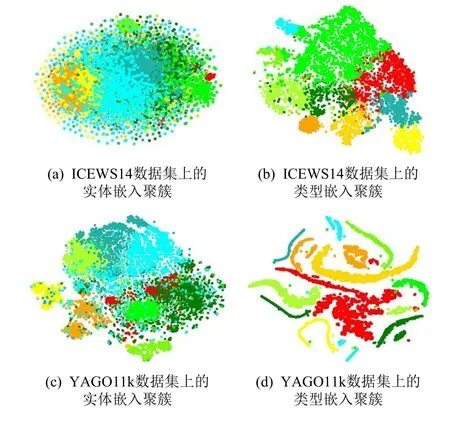
Fig.3 The visualization of entity and type embedding clustering图3 实体和类型嵌入聚簇的可视化

从图3 中可以看出，类型嵌入的簇比实体嵌入的簇更紧凑，且簇与簇之间的区分更明显，而实体嵌入却没有这种明显的聚簇现象. 说明类型嵌入确实能够有效捕获实体的一般语义特征，学习实体中隐含的类型信息.

3.7 参数敏感性分析

为了研究T-Temp 模型中的参数对其性能的影响，本文在ICEWS14 数据集上对一些重要的超参进行了细粒度的分析和比较，包括2 个嵌入向量空间的维度d和k以及训练总轮数N. 令嵌入向量空间的维度分别为d∈{1 600,1 800,2 000,2 200,2 400,2 600,2 800}和k∈{10,15,20,25,30,35,40}，训练总轮数为N∈{30,40,50,60,70,80,90,100}. 为了实验公平，除了当前研究的超参外，其余超参的设置与3.3 节中的相同，实验结果如图4 所示.

图4（a）显式了当维度为d的嵌入向量空间取不同维度值时T-Temp 模型的各项评价指标变化趋势.从图4（a）中可以看出，当维度小于2 000 时，各项指标随维度的增加呈上升趋势，并在维度取值为2 000时达到最大；当维度大于2 000 后，各项指标随维度的增加呈缓慢下降趋势. 维度为d的嵌入向量空间用来表示实体的个体语义信息，实验结果说明该向量空间的维度是个敏感参数，当维度取值过小时，可能造成欠拟合问题，即向量空间无法充分表达所有实体的丰富语义信息；而当维度取值过大时，则可能出现过拟合现象，从而导致性能变差.

图4（b）显式了当维度为k的嵌入向量空间取不同维度值时，T-Temp 模型的各项评价指标变化趋势.从图中4（b）可以看出，模型的各项指标同样随维度的增加先呈上升趋势，然后在维度为20 时达到最大值，随后开始缓慢下降. 维度为k的嵌入向量空间用来表示实体所属的类型信息，实验结果同样说明该向量空间的维度是个敏感参数，其取值过小或过大可能造成模型的欠拟合或过拟合问题. 此外，实体的类型特征所包含的一般语义信息通常没有实体的个体语义信息丰富，因此实验中2 个嵌入向量空间的最佳取值维度有k≪d.

图4（c）显式了当训练总轮数N取不同值时，TTemp 模型的各项评价指标变化趋势. 从图4（c）中可以看出，当训练轮数增加时，模型的各评价指标均有所提升. 而当训练轮数进一步增加时，各项指标逐渐趋于平稳，模型达到一个相对稳定的状态.

3.8 案例研究

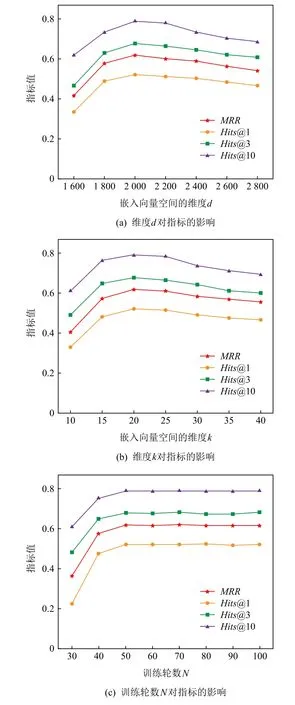
Fig.4 The sensitivity analysis of parameters图4 参数敏感性分析

为了更细致地展示T-Temp 模型确实可以利用时间信息来提高链接预测任务的准确性，本文从YAGO11k 数据集中抽取出一些带有时间信息的四元组作为典型案例进行研究，包括：（Ashley Cole, plays for, Arsenal, [1999—2006]）（Ashley Cole, plays for, Chelsea,[2006—2014]）（Ashley Cole, plays for, A.S. Roma,[2014—2016]）（Ashley Cole, plays for, LA Galaxy,[2016—2019]） . 这些四元组的头实体和关系均是“Ashley Cole”和“Playsfor”，而尾实体则随着时间的不同而有所不同，说明该球员在不同时期曾服务于不同的足球俱乐部.

实验分为2 种情况进行对比：1）掩去四元组中的尾实体，在已知头实体、关系和时间戳的情况下通过模型来预测尾实体，即回答问题：（Ashley Cole, plays for, ?, [1999—2006]）（Ashley Cole, plays for, ?,[2006—2014]）（Ashley Cole, plays for, ?, [2014—2016]）（Ashley Cole, plays for, ?, [2016-2019]）；2）是将四元组中的尾实体和时间戳均掩去，通过训练好的模型来预测尾实体，即回答问题（Ashley Cole, plays for, ?）. 模型根据得分函数对所有候选实体组成的元组计算得分，并按照得分高低依次进行排序，实验结果如表6所示.

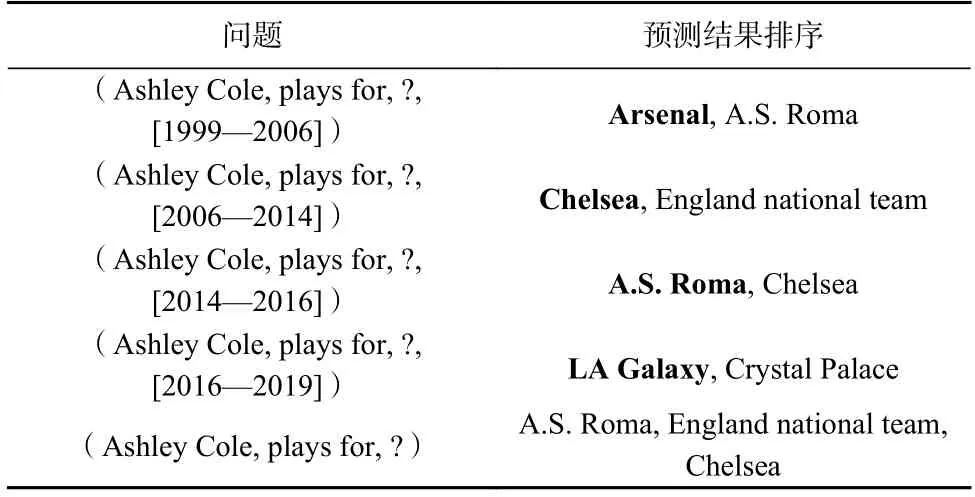
Table 6 Comparison of Link Prediction表6 链接预测对比

从表6 中可以看出，在回答有具体时间范围限制的问题时，模型预测结果排名第一的候选实体均为正确答案，说明T-Temp 模型确实可以利用可提供的时间信息实现更精准的链接预测. 而回答不带有时间戳的三元组问题时，模型则给出了若干个候选实体作为答案. 这些候选实体虽然无法给出用户精准的答案，但得益于T-Temp 模型的类型限制作用，他们都属于“足球俱乐部”这一类型，一定程度上满足了用户的需求.

4 总结与展望

时态知识图谱表示学习是近几年的研究热点之一. 本文基于张量的典范多元分解技术，提出了一种类型增强的时态知识图谱表示学习模型T-Temp，用于解决时态知识图谱补全和语义计算问题，并证明了该模型在理论上具有完全表达性和较低的时空消耗. T-Temp 模型在表示学习的过程中不仅可以利用可提供的各种形式的时间信息，还可以利用实体和关系间的类型兼容性，自动学习实体、关系、时间和类型的嵌入表示，不需要提供额外的类型信息. 在4个公开的时态知识图谱数据集上进行的大量实验结果证明了T-Temp 模型的有效性.

鉴于现有的时态知识图谱中，与事实相关联的时间戳存在大量的缺失现象，下一步，计划探索TTemp 模型对缺失的时间戳进行预测和补全的问题.另外，如何将T-Temp 模型扩展到开放世界假设[51]，实现对未来事件的推理和预测，也是值得深入研究的方向.

作者贡献声明：何鹏提出了算法思路，完成实验并撰写论文；周刚、陈静、章梦礼、宁原隆提出指导意见并修改论文.