双曲正切高斯与两阶段反向学习平衡优化算法

李守玉,何 庆,陈 俊

(贵州大学 大数据与信息工程学院,贵阳 550025) E-mail：qhe@gzu.edu.cn

1 引 言

为了更好解决现实中的复杂优化问题,研究者们通过观察、研究自然界中生物的进化或物体存在的物理现象,提出了遗传算法、粒子群算法、蚁群算法及灰狼算法等元启发式算法,并在工程领域取得不错的成果.

然而传统的遗传算法[1]易出现的局部搜索精度不高且算法执行效率低;粒子群算法[2]虽收敛速度快、易于实现,但存在早熟现象;蚁群算法[3]虽有较强的记忆性,但它容易出现停滞现象且效率低.平衡优化算法[4](Equilibrium Optimizer,EO)由Faramarzi于2019年提出的基于物理的元启发式算法.EO的寻优过程是在动态和平衡状态的控制体积-质量平衡模型中,帮助模型中的粒子找寻平衡状态.该算法与遗传算法和粒子群算法相比,具备较强的竞争力,同时它具有参数少、执行效率高及易于部署等优点.因此,它被成功应用到阈值图像分割[5],多目标优化[6],优化太阳能抛物面收集器的热性能参数[7],光伏电池参数估计[8]等科学领域.

然而平衡优化器算法与大多启发式算法一样存在易陷入局部最优且收敛速度慢等问题.为此,研究者提出了不同的改进策略.文献[9]通过引入反向学习和改进浓度更新公式,提高算法寻优精度及加快算法收敛.文献[10]利用混沌映射建立的搜索机制,改善算法寻优性能并应用于特征选择.文献[11]将拉普拉斯分布与反向学习结合增强开发能力,达到快速收敛的目的.文献[12]将热交换优化与平衡优化器结合提高算法的优化性能.文献[13]利用对立学习和逃逸策略提高算法的勘探能力.虽然上述算法对优化性能有一定提升,但收敛速度慢的问题仍然存在以及未同时考虑提高全局与局部寻优能力.

针对平衡优化算法存在的问题,本文提出了双曲正切高斯与两阶段反向学习的平衡优化算法(HEO-OBL),将双曲正切函数与黄金分割数融入高斯分布中,增强算法的全局搜索能力;利用遗传算法中的交叉和变异,缓解种群迭代后期多样性减少;通过两阶段方向学习,使用不同的反向学习平衡全局与局部搜索能力并加快算法收敛.

2 平衡优化算法

2.1 种群初始化

EO算法也是通过随机初始化生成初始种群：

(1)

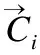
2.2 均衡池

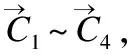
(2)

2.3 浓度更新

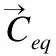
(3)

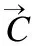
(4)

(5)

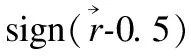
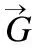
(6)

(7)

(8)

(9)

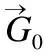
3 双曲正切高斯与两阶段反向学习平衡优化算法

3.1 双曲正切高斯因子

文献[14]充分发挥黄金分割数的优势提出黄金正弦算法,其在解决函数优化问题取得较好的成果.文献[15]利用黄金正弦作为中间媒介,提高蝴蝶算法的优化能力.另外,文献[16]利用双曲正切函数代替传统开关函数,增强滑模观测器的抗干扰性和稳定性.文献[17]借助双曲正切函数的变化特性,实现风机箱变熔断器与集电线路之间反时限动作特性配合,证明了黄金分割数和双曲正切函数行之有效.

基本EO算法中平均候选解对算法的全局搜索和局部搜索起重要的作用,为了进一步增强其对算法的影响,提出了双曲正切高斯因子.该策略主要利用双曲正切函数的变化特性以及黄金分割数的优势对高斯分布进行改造,进而加强算法寻优能力.除此之外,将将种群的迭代信息融入双曲正切函数,使其的变化更符合种群进化规律.具体改造如下：

(10)

(11)

N(gn,th)

(12)

文中采用高斯分布N(a,b),其中a表示均值,b表示方差.将式(1)和式(2)融入高斯分布中,得到双曲正切高斯因子.gn为黄金分割数且充当高斯分布的均值,使高斯分布具备它的优势,增强算法的全局搜索能力,另外,th为融入迭代信息的双曲正切函数.同时,它作为高斯分布的方差能够根据种群进化过程,动态调整分布,达到自学习进化规律的目的,从而提高平衡全局与局部搜索的能力.它通过如下方式作用平均候选解.

Cave=CaveN(gn,th)

(13)

3.2 交叉变异混合策略

基本EO算法存在迭代后期种群多样性逐渐减少,导致出现早熟现象,从而影响算法的优化精度.因此,借助遗传算法中交叉和变异操作增强种群多样性.文中交叉操作在增强种群多样性占主导作用,变异起辅导作用.交叉依据较大的交叉概率,对种群中个体位置进行交叉,得到新的个体位置;变异则是以较小的变异概率对种群个体进行变异,生成新个体;两者协同配合进一步增加种群个体多样性,进而提升种群多样性.交叉概率和变异概率在增强种群多样性环节扮演重要的角色,对两者的定义如式(14)和式(15).

交叉概率定义如下：

(14)

变异概率定义如下：

(15)

为了充分发挥交叉与变异的优势,文中将交叉概率设为0.8,变异概率设为0.08.

3.3 两阶段反向学习策略

为了更进一步加快算法收敛,利用反向学习中反向解的思想,提出两阶段反向学习策略.其核心原理是对浓度更新之后个体求取反向解,再通过贪心算法择优进入下一次循环.反向点定义：若p(x1,x1,…,xn)是n维坐标系中的一个点,x1,x1,…,xn∈R,同时满足xi∈[ai,bi],则反向点完全由坐标确定.

(16)

两阶段反向学习策略,其一是随机反向学习;其二是基本反向学习.该策略通过随机产生[0,1]的随机数与切换概率比P较大小,进而为算法选择不同阶段的反向学习.在文中,切换概率设为P=0.5.

若P小于该随机数,则选择基本反向学习：

(17)

若P大于该随机数,则选择随机反向学习：

(18)

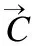
虽然两阶段反向学习策略产生新的个体一定程度加快算法收敛,但是不能保证产生的新解一定优于原位置的解,因此,使用贪心思想进行择优.

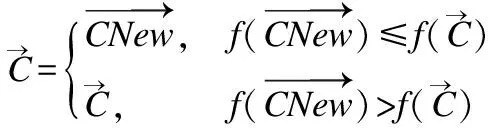
(19)

3.4 算法流程图

文中所提双曲正切高斯与两阶段反向学习平衡优化算法的算法流程,如图1所示.

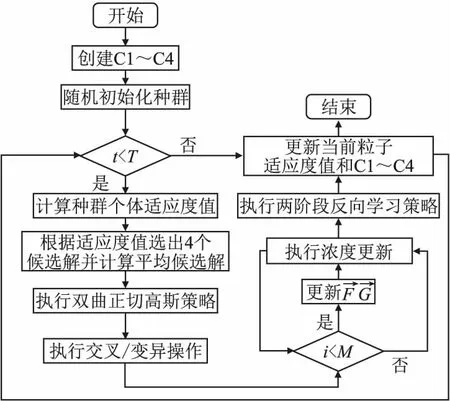
图1 算法流程Fig.1 Algorithm flow

Step1.算法初始阶段,先创建用于存储候选解的C1～C4.

Step2.采用随机初始化的方式对种群中的个体位置进行初始化.

Step3.进入大循环,迭代更新种群个体位置,直到满足迭代停止条件.

Step4.计算种群个体的适应度,并对根据4个候选解计算平均候选解.

Step5.通过4个候选解C1～C4求出平均候选解,然后利用双曲正切高斯策略提高平均候选解的全局与局部搜索能力.

Step6.执行完Step 5后,对种群中的每个个体先执行交叉操作,然后执行变异操作,提高种群多样性.

Step7.进入个体浓度循环阶段,直到满足迭代停止条件.

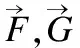
Step9.执行浓度更新,然后转Step 7.

Step10.利用两阶段反向学习策略,加速算法收敛,然后转Step 3.

4 实验与仿真分析

实验环境为Windows7,64位操作系统,CPU为Inter Core i5-6500H,主频3.2GHz,内存8GB,算法在MATLAB2014b上运行.

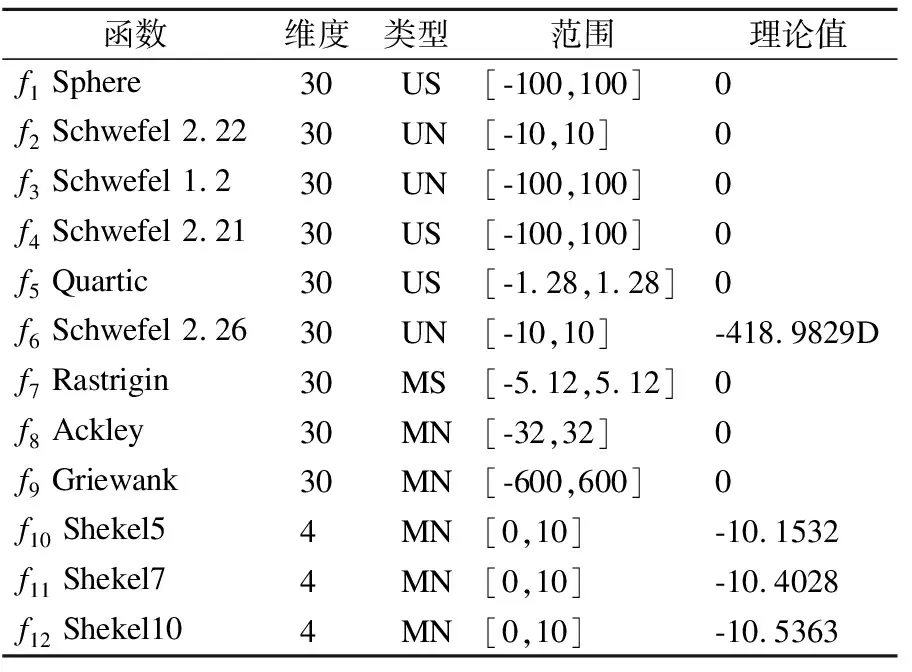
表1 基准测试函数Table 1 Benchmark function

为了测试HEO-OBL算法的鲁棒性和有效性,使用12个含有单峰可分、单峰不可分、多峰可分多峰不可分等类型基准测试函数,其中f10～f12为Shekel函数系列,求和上限分别取5、7以及10的函数,如表1所示.

表2 算法参数Table 2 Parameters of algorithm

同时,为保证对比的公平性,算法基本参数设置相同：种群规模为30,最大迭代次数500,独立运行30次.另外,算法的初始对于其寻优性能也会产生相应的影响,因此,初始参数参照相关文献进行设置,如表2所示.

4.1 各策略与常见算法性能分析

表3通过最优值、平均值、标准差、成功率以及平均耗时(s)等5个性能指标来评估各算法的性能,对比数据如表3所示.其中,最优值和最差值展现算法的寻优上限和下限,从算法最好状态以及最差状态了解寻优能力;平均值则反映算法在30次独立运行后,算法寻优能力和收敛速度的综合体现;标准差则体现了算法寻优过程中算法的稳定程度;平均耗时可以看出算法执行效率.另外,为了充分验证HEO-OBL的有效性和鲁棒性,将HEO-OBL与双曲正切高斯因子(EO1)、交叉变异混合策略(EO2)、两阶段反向学习策略(EO3)、灰狼算法(Grey Wolf Optimizer,GWO)、鲸鱼算法(Whale Optimization Algorithm,WOA)与蝗虫算法(Grasshopper Optimization Algorithm,GOA)进行对比.

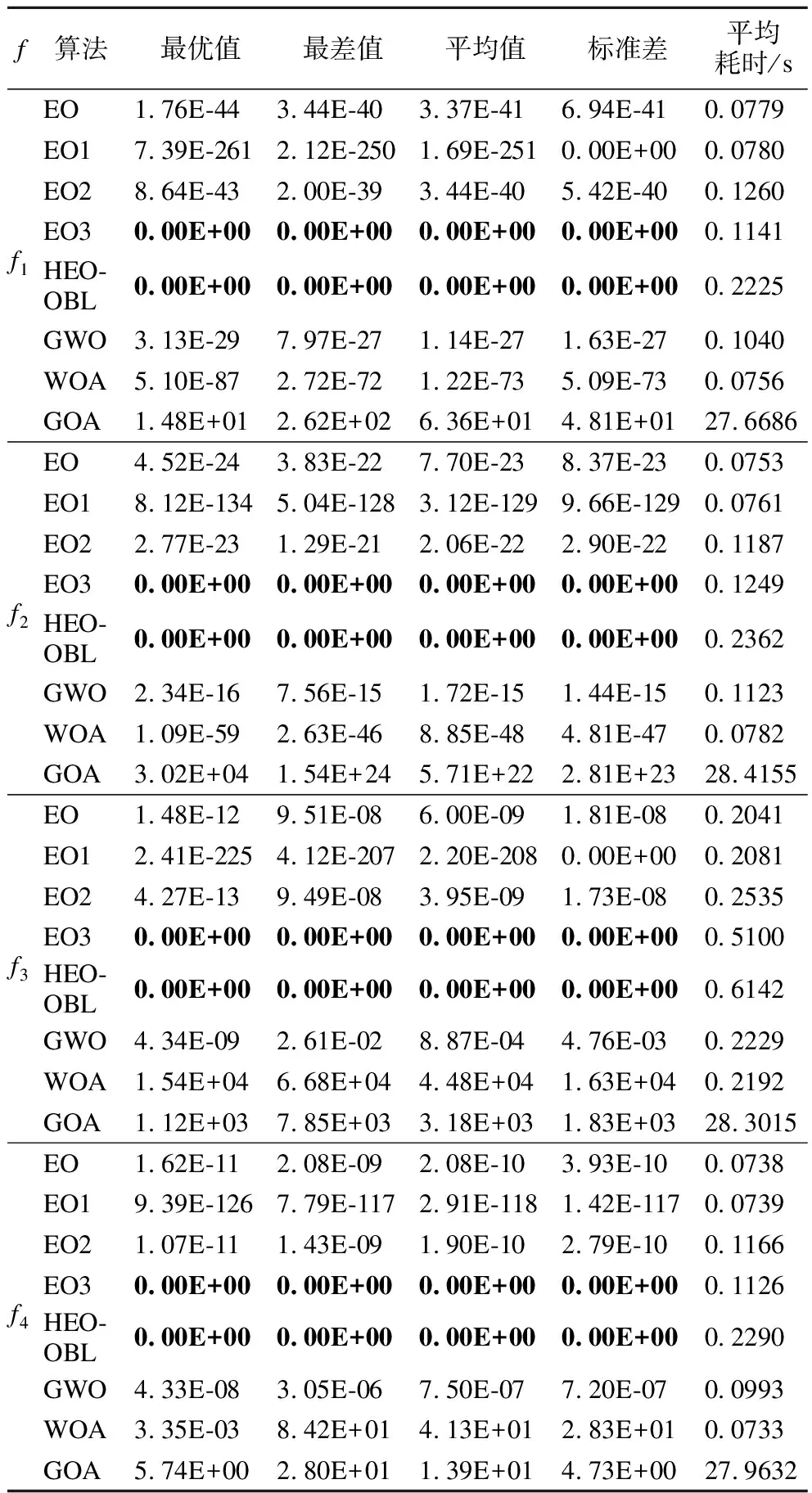
表3 基准测试函数结果对比Table 3 Comparison of benchmark function results

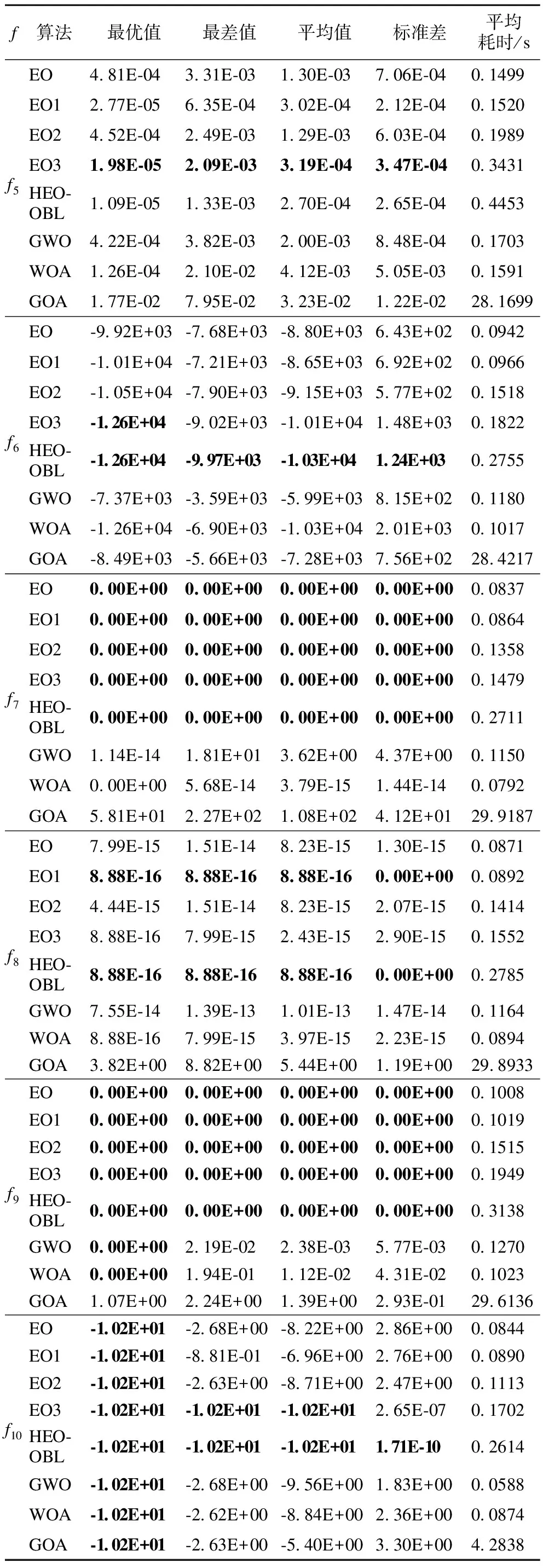
f算法最优值最差值平均值标准差平均耗时/sEO4.81E-043.31E-031.30E-037.06E-040.1499EO12.77E-056.35E-043.02E-042.12E-040.1520EO24.52E-042.49E-031.29E-036.03E-040.1989f5EO31.98E-052.09E-033.19E-043.47E-040.3431HEO-OBL1.09E-051.33E-032.70E-042.65E-040.4453GWO4.22E-043.82E-032.00E-038.48E-040.1703WOA1.26E-042.10E-024.12E-035.05E-030.1591GOA1.77E-027.95E-023.23E-021.22E-0228.1699EO-9.92E+03-7.68E+03-8.80E+036.43E+020.0942EO1-1.01E+04-7.21E+03-8.65E+036.92E+020.0966EO2-1.05E+04-7.90E+03-9.15E+035.77E+020.1518f6EO3-1.26E+04-9.02E+03-1.01E+041.48E+030.1822HEO-OBL-1.26E+04-9.97E+03-1.03E+041.24E+030.2755GWO-7.37E+03-3.59E+03-5.99E+038.15E+020.1180WOA-1.26E+04-6.90E+03-1.03E+042.01E+030.1017GOA-8.49E+03-5.66E+03-7.28E+037.56E+0228.4217EO0.00E+000.00E+000.00E+000.00E+000.0837EO10.00E+000.00E+000.00E+000.00E+000.0864EO20.00E+000.00E+000.00E+000.00E+000.1358f7EO30.00E+000.00E+000.00E+000.00E+000.1479HEO-OBL0.00E+000.00E+000.00E+000.00E+000.2711GWO1.14E-141.81E+013.62E+004.37E+000.1150WOA0.00E+005.68E-143.79E-151.44E-140.0792GOA5.81E+012.27E+021.08E+024.12E+0129.9187EO7.99E-151.51E-148.23E-151.30E-150.0871EO18.88E-168.88E-168.88E-160.00E+000.0892EO24.44E-151.51E-148.23E-152.07E-150.1414f8EO38.88E-167.99E-152.43E-152.90E-150.1552HEO-OBL8.88E-168.88E-168.88E-160.00E+000.2785GWO7.55E-141.39E-131.01E-131.47E-140.1164WOA8.88E-167.99E-153.97E-152.23E-150.0894GOA3.82E+008.82E+005.44E+001.19E+0029.8933EO0.00E+000.00E+000.00E+000.00E+000.1008EO10.00E+000.00E+000.00E+000.00E+000.1019EO20.00E+000.00E+000.00E+000.00E+000.1515f9EO30.00E+000.00E+000.00E+000.00E+000.1949HEO-OBL0.00E+000.00E+000.00E+000.00E+000.3138GWO0.00E+002.19E-022.38E-035.77E-030.1270WOA0.00E+001.94E-011.12E-024.31E-020.1023GOA1.07E+002.24E+001.39E+002.93E-0129.6136EO-1.02E+01-2.68E+00-8.22E+002.86E+000.0844EO1-1.02E+01-8.81E-01-6.96E+002.76E+000.0890EO2-1.02E+01-2.63E+00-8.71E+002.47E+000.1113f10EO3-1.02E+01-1.02E+01-1.02E+012.65E-070.1702HEO-OBL-1.02E+01-1.02E+01-1.02E+011.71E-100.2614GWO-1.02E+01-2.68E+00-9.56E+001.83E+000.0588WOA-1.02E+01-2.62E+00-8.84E+002.36E+000.0874GOA-1.02E+01-2.63E+00-5.40E+003.30E+004.2838

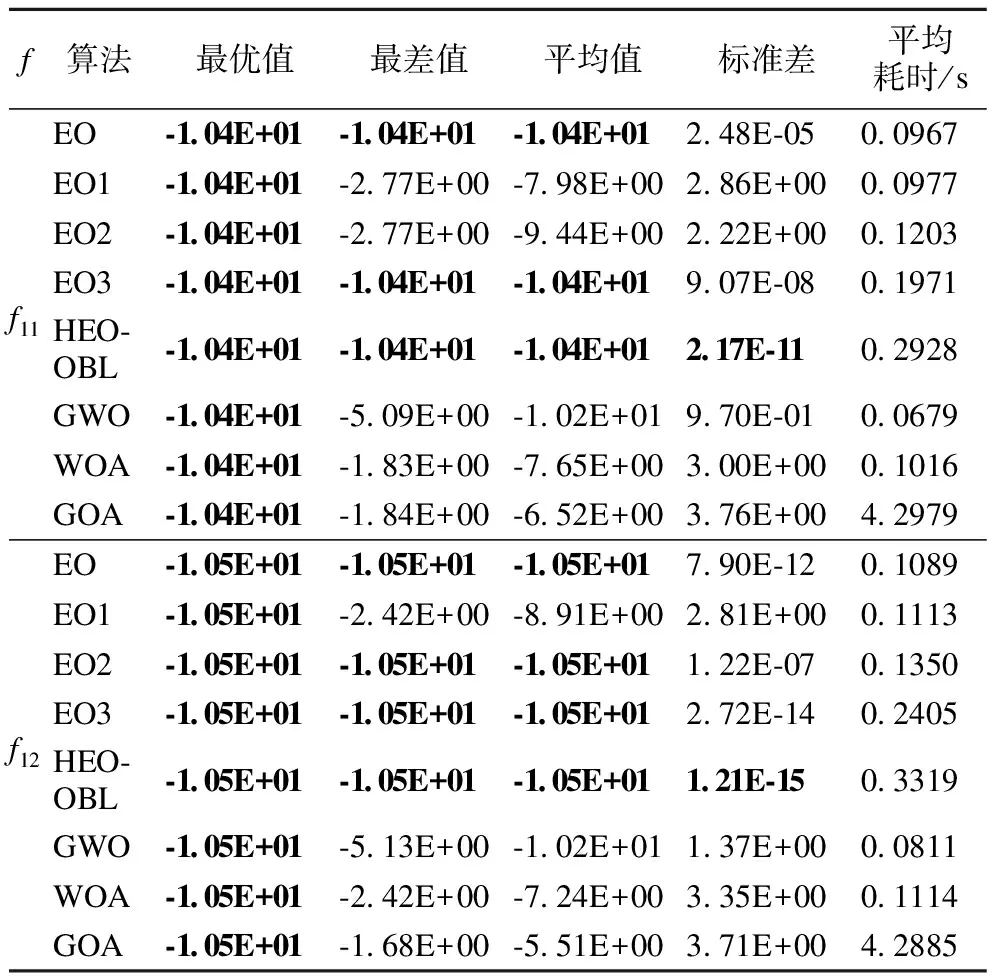
f算法最优值最差值平均值标准差平均耗时/sEO-1.04E+01-1.04E+01-1.04E+012.48E-050.0967EO1-1.04E+01-2.77E+00-7.98E+002.86E+000.0977EO2-1.04E+01-2.77E+00-9.44E+002.22E+000.1203f11EO3-1.04E+01-1.04E+01-1.04E+019.07E-080.1971HEO-OBL-1.04E+01-1.04E+01-1.04E+012.17E-110.2928GWO-1.04E+01-5.09E+00-1.02E+019.70E-010.0679WOA-1.04E+01-1.83E+00-7.65E+003.00E+000.1016GOA-1.04E+01-1.84E+00-6.52E+003.76E+004.2979EO-1.05E+01-1.05E+01-1.05E+017.90E-120.1089EO1-1.05E+01-2.42E+00-8.91E+002.81E+000.1113EO2-1.05E+01-1.05E+01-1.05E+011.22E-070.1350f12EO3-1.05E+01-1.05E+01-1.05E+012.72E-140.2405HEO-OBL-1.05E+01-1.05E+01-1.05E+011.21E-150.3319GWO-1.05E+01-5.13E+00-1.02E+011.37E+000.0811WOA-1.05E+01-2.42E+00-7.24E+003.35E+000.1114GOA-1.05E+01-1.68E+00-5.51E+003.71E+004.2885

从表3可以看出,在f1～f12函数上,HEO-OBL的5个性能评估指标均优于单个改进策略和其他算法,证明HEO-OBL能够兼容3个改进策略且充分发挥它们的优势,帮助提高算法的寻优精度和加快收敛速度.从改进策略角度看,在f1～f6和f10函数上的EO1的最优值和最差值相较于EO寻优精度更高.这也充分说明加入双曲正切高斯因子,有助于改善算法寻优的上限及下限,算法寻优精度提升显著;虽然EO2的寻优精度提高不明显,在f1～f2函数上略低于EO,但f4～f6和f8函数上均要优于EO.EO2通过交叉和变异操作保持种群多样性对于HEO-OBL的意义十分重大;在f1～f4函数上EO3的5个性能评估指标均能寻到理论值,f5～f6和f8函数上,精度仅次于HEO-OBL.这验证了两阶段反向学习能够综合提高EO的综合寻优能力.此外,3个改进策略在f7、f9和f10～f12函数上寻优性能与EO相同并且在多个函数的寻优精度也高于GWO、GOA和WOA.从平均耗时看,GOA的耗时最长,算法执行效率低且精度最差;EO、EO1、WOA的耗时相差不大;EO3和GWO的耗时在一个量级;相对于EO、EO1、EO2、EO3、WOA和GWO,HEO-OBL的耗时略有增加,主要因为HEO-OBL需要执行对个体的交叉、变异以及两阶段的反向解,但从算法总体寻优结果和执行效率考虑,HEO-OBL增加的耗时在接受范围.

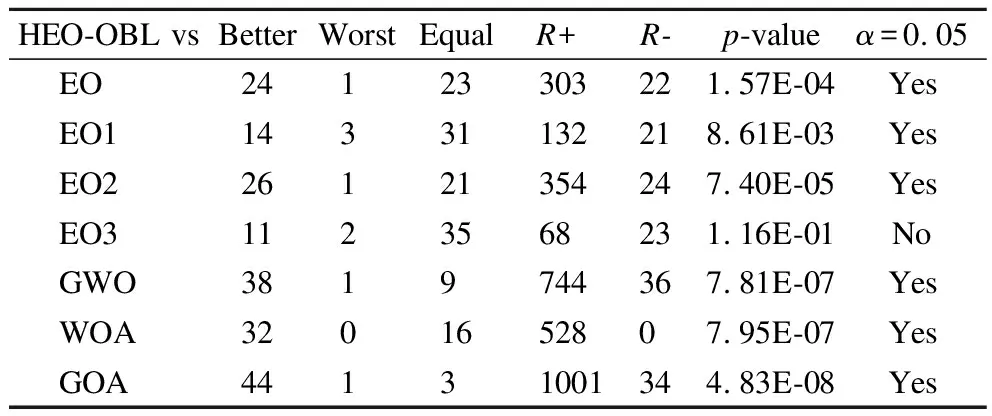
表4 8种算法在0.05显著性水平下的Wilcoxon检验结果Table 4 Wilcoxon test results of the 8 algorithms at 0.05 significance level

Derrac等人[18]指出对改进进化算法应该进行统计检验.因为平均值和标准差不会比较算法的每次运算结果,所以需要通过统计检验.本文主采用wilcoxon和Friedman两种非参数检验方法进行统计检验,前者验证两个算法之间的显著差异性,后者则通过秩均值衡量算法的性能,秩均值越小,算法性能越好,反之亦然.两种检验方法主要针对每个算法的寻优能力的检验,即各算法在12个测试函数上的最优值、最差值、平均值和标准差4个性能指标进行检验.表4列出了8种算法在0.05显著性水平下的wilcoxon检验的结果.

从表4中可以看出,除了“HEO-OBL vs EO3”,其余情况下,HEO-OBL的R+和R-值都较高,p-value值都小于0.05.这意味着除了EO3之外,HEO-OBL和其他算法之间的性能差异显著.

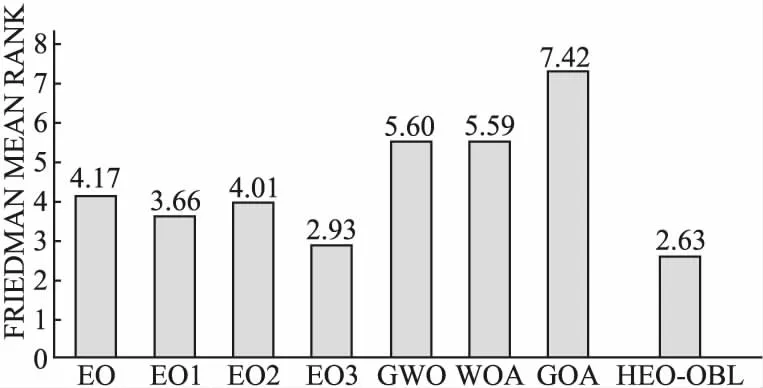
图2 8种算法在12个基准函数上Friedman检验的秩均值Fig.2 Rank mean of the Friedman test on 12 benchmark functions of 8 algorithms

基于Friedman秩检验,图2显示了12个函数上的8种算法的秩均值.如图2所示,HEO-OBL得到了最小的秩均值,其次是EO3、EO1、EO2、EO、WOA、GWO和GOA.这又一次证明HEO-OBL以及改进策略的有效性和竞争性.

4.2 收敛性分析

为了更好的观测HEO-OBL及其他算法的寻优过程,图3给出部分基准测试函数的平均收敛曲线图,各算法的曲线图例与图3(a)一致.此外,为了便于观察曲线的收敛情况,除了图3(b),其余曲线的纵坐标取以10为底的对数.

从图3(a)～图3(e)能够看出,迭代前期HEO-OBL、EO1和EO3曲线下降速度很快且寻优精度都高于EO,说明加入双曲正切高斯因子和两阶段反向学习能够增强算法跳出局部最优的能力,使得算法在迭代开始时收敛速度变快,有助于大幅度提高EO算法的全局搜索能力.随着算法进入迭代后期,GOA发生最严重的停滞,GWO和WOA次之,算法过早陷入局部最优,而HEO-OBL得益于改进策略的有效融合,在整个寻优过程中保持最强的寻优能力.除此之外,在图3(a)～图3(c)中,相比单个策略及其他算法,HEO-OBL能够快速收敛到更高的寻优精度;尤其图3(c)中,除GOA和GWO外都能寻到理论值,但HEO-OBL的收敛速度最快,EO1、EO3、EO2、EO紧随其后.在图3(d)中,EO1最后的收敛精度与HEO-OBL在同一个量级,EO2的寻优精度与EO相似;图3(d)～图3(e)中,EO3的寻优精度与HEO-OBL最为接近,高于其他算法.这也充分印证上述HEO-OBL以及3个改进策略的有效性,并且具备出色的收敛能力.

结合表3的实验结果和图3的收敛曲线图证明,不管基准测试函数是单峰、多峰,HEO-OBL的综合性能均比其他算法要好.图3(c)因纵坐标取对数的原因加上算法寻到0后曲线后面就没有显示.

4.3 与新改进智能算法对比

为了进一步研究HEO-OBL优化性能,将其与新改进的(modified Equilibrium Optimizer,m-EO)[9]、(Opposition-based

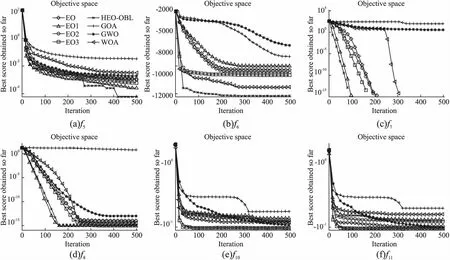
图3 各算法的平均收敛曲线Fig.3 Average convergence curves of each algorithm

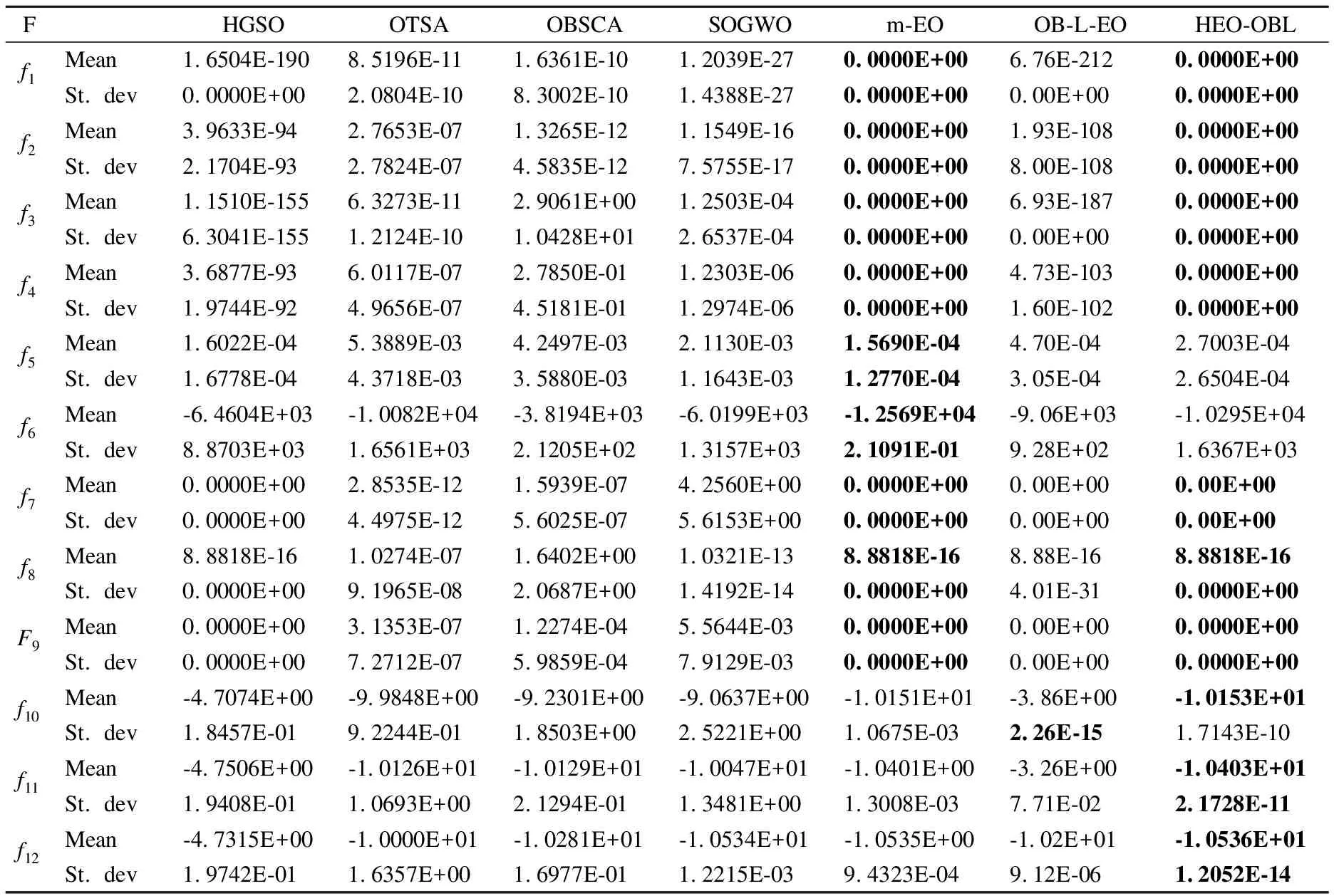
表5 与新改进算法对比Table 5 Compared with the new improved algorithm

Laplacian Equilibrium Optimizer,OB-L-EO)[11],其他新改进算法,如亨利气体溶解度优化(Henry gas solubility optimization,HGSO)[19]、改改进的模拟退火算法(Improved Simulated Annealing algorithm,OTSA)[20]、改进的正余弦算法(improved Opposition-Based Sine Cosine Algorithm OBSCA)[21]和改进的灰狼算法(Selective opposition basedgrey wolf optimization,SOGWO)[22]进行对比.同时,为了确保对比的公平性,HEO-OBL的参数设置与文献[9]保持一致,即种群规模为30,函数维度为30,最大迭代次数为500,独立运行30次.其中,HGSO、OTSA、OBSCA和SOGWO的数据源自文献[9].最终结果如表5所示,最优结果已黑体表示.

从表5可知,HEO-OBL在12个函数上的整体性能都优于HGSO、OTSA、OBSCA和SOGWO.HEO-OBL在10个函数上获得更高的精度比m-EO的函数还多一个.与OB-L-EO相比,HEO-OBL在所有函数上的优化效果更好,除了f10上的标准差.在众多新改进的算法中,HEO-OBL出色的优化性能离不开改进策略的贡献,双曲正切高斯因子利用正切变化动态提高算法的全局和局部搜索能力,利于扩大搜索空间的寻优范围;选择与交叉最大城堡度保留种群多样性,避免种群多样性流失;两阶段反向学习从收敛速度角度,不仅加快算法的收敛速度,还可提高收敛精度,3个改进策略有效的结合才使HEO-OBL具备更强的优化能力.

4.4 时间复杂度分析

HEO-OBL算法的时间复杂度如下：假设种群规模为N,搜索空间维度为D,则EO的随机初始化的时间复杂度为O(N×D),计算个体适应度为O(N),迭代过程中的时间复杂度为O(N×D),浓度更新的时间复杂度为O(N),EO总的时间复杂度为O(N×D).

同理,HEO-OBL加入的双曲正切高斯因子时间复杂度为O(1),增加的交叉变异混合策略时间复杂度由交叉的时间复杂度为O(N×D)和变异的时间复杂度为O(N),增加的两阶段的时间复杂度为O(N×D),因此HEO-OBL总的时间复杂度O(N×D).因为HEO-OBL和EO的时间复杂度一样,所以HEO-OBL并未对算法产生负面影响.

4.5 与新改进算法在CEC2014上的对比分析

为了进一步研究HEO-OBL在复杂优化函数上的寻优性能.文中采用智能算法领域常用评估优化能力的CEC2014函数集进一步测试HEO-OBL整体优化性能.该函数集远比表1中12个经典基准测试函数更为复杂.CEC2014的30个测试函数主要被划分为4类,即单峰函数(F1-F3)、多峰函数(F4-F16)、混合函数(F17-F22)和复合函数(F23-F30).文献[23]提供了30个函数的详细信息.

将HEO-OBL算法与新改进粒子群算法和改进的灰狼算法进行对比,其中带时变加速系数的改进粒子群算法(Improved PSO with time-varying accelerator coefficients,IPSO[24])、具有自适应加速度系数的改进粒子群算法(modified PSO with adaptive accelerationcoefficients,TACPSO[25])、动态维度搜索灰狼算法(Dynamically Dimensioned Search Grey Wolf Optimizer,DGWO[26])和带有加权距离的灰狼算法(Grey Wolf Optimizer with a novel weighted distance,GWO-WD[27])算法进行比较.同时,为了确保对比公平,算法的参数与GWO-WD原文献设置一致,即种群大小为30,CEC2014

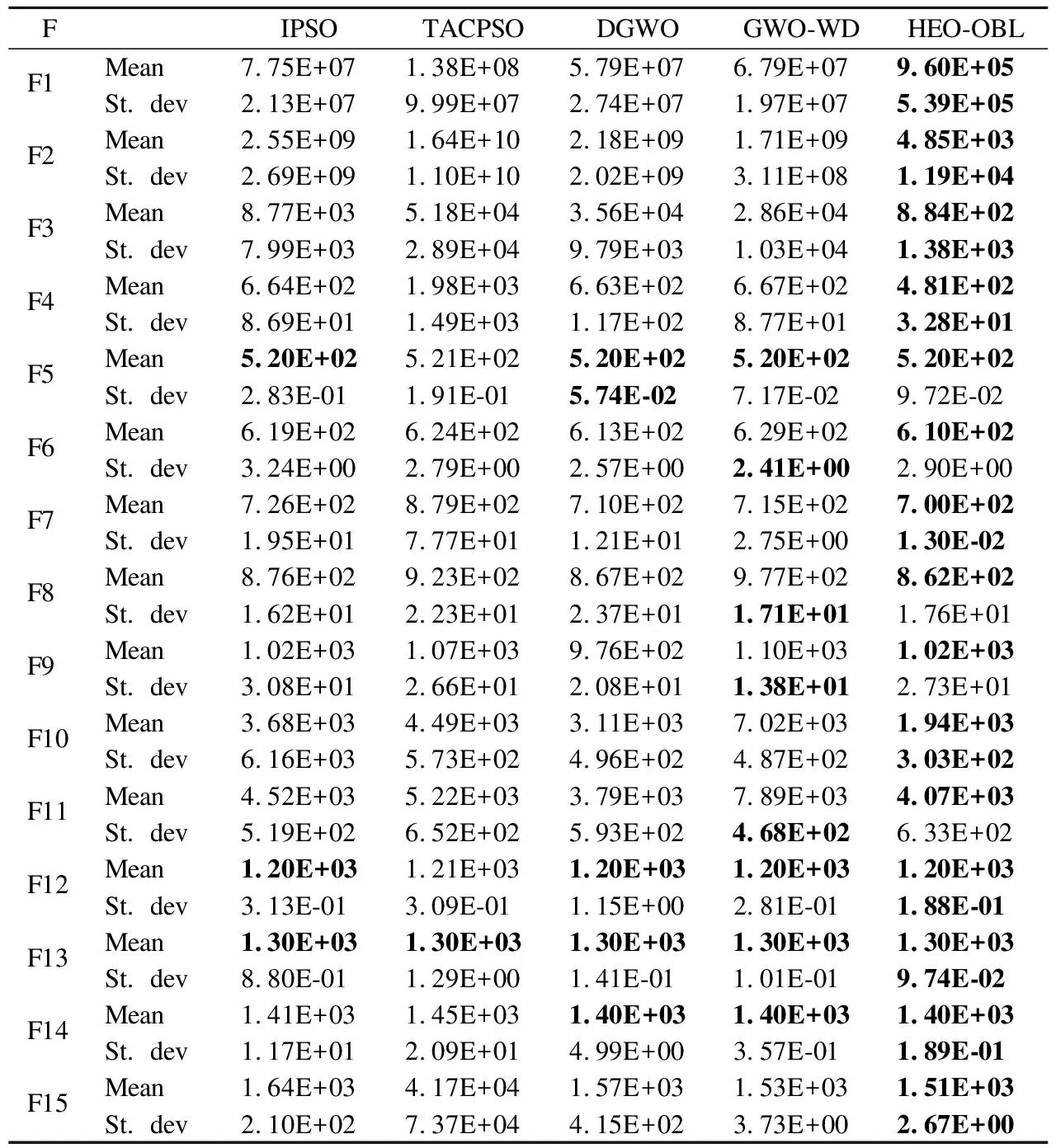
表6 CEC2014测试函数结果对比Table 6 Comparison of CEC2014 function results

FIPSOTACPSODGWOGWO-WDHEO-OBLF16Mean5.17E+061.61E+031.61E+031.61E+031.61E+03St. dev7.06E+055.48E-016.28E-013.37E-015.65E-01F17Mean6.91E+064.14E+062.13E+064.47E+062.45E+05St. dev2.61E+052.87E+063.93E+052.11E+062.00E+05F18Mean1.94E+039.93E+072.14E+072.56E+075.18E+03St. dev3.13E+012.70E+083.13E+066.96E+063.31E+03F19Mean5.26E+032.01E+031.94E+031.98E+031.91E+03St. dev2.62E+036.35E+013.00E+013.59E+012.16E+00F20Mean5.26E+031.74E+041.95E+041.63E+047.08E+03St. dev2.62E+031.73E+039.63E+036.59E+033.37E+03F21Mean1.68E+057.15E+051.42E+051.20E+061.16E+05St. dev1.21E+058.92E+052.92E+046.77E+051.01E+05F22Mean2.71E+032.86E+032.56E+032.83E+032.65E+03St. dev5.77E+001.96E+021.76E+022.20E+022.19E+02F23Mean2.63E+032.68E+032.63E+032.52E+032.50E+03St. dev1.21E+013.88E+011.18E+013.69E+010.00E+00F24Mean2.64E+032.68E+032.60E+032.60E+032.60E+03St. dev1.19E+011.64E+011.53E-031.53E-052.53E-07F25Mean2.71E+032.72E+032.71E+032.70E+032.70E+03St. dev5.77E+005.08E+005.24E+002.95E-130.00E+00F26Mean2.73E+032.72E+032.75E+032.70E+032.75E+03St. dev6.23E+016.35E+015.08E+019.05E-055.05E+01F27Mean3.53E+033.78E+033.35E+033.29E+032.90E+03St. dev2.48E+028.68E+011.19E+23.46E+020.00E+00F28Mean4.36E+034.50E+033.96E+033.42E+033.00E+03St. dev3.87E+026.12E+022.93E+024.57E+020.00E+00F29Mean2.18E+071.64E+071.01E+065.12E+058.78E+05St. dev1.68E+071.47E+072.13E+061.75E+051.86E+06F30Mean6.04E+041.14E+054.07E+045.79E+048.24E+03St. dev6.63E+047.79E+042.37E+043.54E+044.01E+03

函数维度设为30,各算法独立运行30次.另外,IPSO、TACPSO、DGWO的数据均来自GWO-WD.均值(Mean)和标准差(St.dev)被用来评估各算法的性能,对比结果记录在表6中.

由表6可知,与IPSO相比HEO-OBL在27个函数获得了更好的结果,在3个函数(F5,F12～F13)获得相似的结果;与TACPSO相比,HEO-OBL在28个函数取得了更高的精度,在2个函数(F13和F16)和取得了类似的结果;与DGWO相比,HEO-OBL在23个函数提供了更好的结果,在6个函数(F5,F12～14,F16和F24)以及1个函数(F22)提供了相似和较差的结果;与GWO-WD相比,HEO-OBL能够在21个函数得到更优的结果,在7个函数(F5,F12～14,F16,F24,F26)个函数(F26和F29)得到相似和较差结果.HEO-OBL与4种改进算法在复杂函数的优化结果对比表明了HEO-OBL不仅在基准测试函数上拥有出色的竞争力,在复杂函数仍具有更强的优化能力.

表7 5种算法在0.05显著性水平下CEC2014的Wilcoxon检验结果Table 7 Wilcoxon test results of CEC2014 for 5 algorithms at the significance level of 0.05

此外,显著性水平为0.05的Wilcoxon秩和检验结果记录在表7中.从该表中,HEO-OBL在所有情况下都获得更高的R+值和R-值并且p-value都小于0.05.这说明HEO-OBL与其他4种新改进算法存在显著差异.同时,Friedman秩检验也被用来评估各算法在CEC2014上的整体性能,5种算法所得的均秩值绘制在图4中.

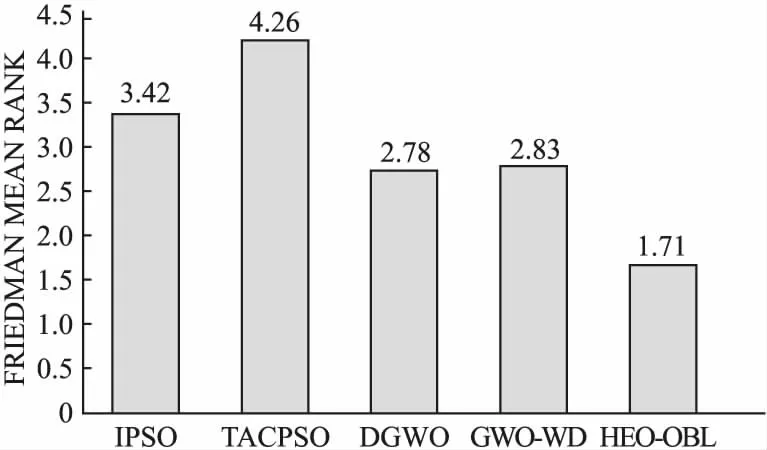
图4 5种算法在CEC2014上Friedman检验的秩均值Fig.4 Rank mean of the 5 algorithms in the Friedman test on CEC2014

从图4可以看出,HEO-OBL取得最小的秩均值,排名第一,其次是DGWO、GWO-WD、IPSO和TACPSO.这也从统计角度说明了HEO-OBL的整体性能非常具有竞争力.

5 结 论

为了缓解EO算法寻优过程中种群多样性减少导致EO算法容易陷入局部最优和加快收敛速度,本文提出了双曲正切高斯与两阶段反向学习平衡优化算法,并应用12个基准测试函数和30个CEC2014复杂函数来验证改进算法的综合性能.双曲正切高斯因子融合黄金分割数、双曲正切函数以及高斯分布的优势,有助于扩大个体的全局搜索范围,提高优化精度;交叉变异混合策略虽然对精度提升效果不显著,但对种群整体多样性的贡献很大;利用两阶段反向学习,个体可以使用不同的反向学习平衡和增强算法的全局和局部搜索能力,从而提高寻优精度和加快算法收敛.另外,本文不仅使用最优值、最差值、平均值、标准差、平均耗时等指标对算法评估,还使用非参数检验Wilcoxon秩和检验对算法进行显著性分析以及Friedman秩检验对算法整体性能分析,实验结果表明HEO-OBL算法具备更好的优化性能且具有出色的竞争力,同时算法的有效性和鲁棒性也得到充分验证.

未来研究准备改进交叉与变异环节确保种群多样性的同时,显著提高寻优精度;同时,考虑将改进的平衡优化算法应用于解决柔性车间调度问题、机器人路径规划等领域,更进一步验证算法的性能.