借助几何直观 培养关键能力
——以2022年中考几何直观试题为例*
潘竹树 (福建省泉州市第九中学 362000)
1 课标引领
《义务教育数学课程标准(2022年版)》指出,初中阶段核心素养主要表现为抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识和创新意识[1]7.几何直观主要是指运用图表描述和分析问题的意识与习惯,能够根据描述画出相应的图形,分析图形的性质;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路[1]8.
几何直观能为学生理解与洞察其他更为抽象的数学内容与结构搭建桥梁,几何直观是启发问题解决思路的基本策略[2].抽象能力是数学思维的基础,只有具备一定的抽象能力,才可能从感性经验中获得事物的本质特征,上升到理念认识[3].几何直观和抽象能力相互依托,几何直观本质上是依托图形展开想象的抽象思维;反之,只有具备一定的抽象能力,才能发展几何直观学习能力,增强运用图形思维的意识,提升数形结合的能力.本文剖析2022年全国部分地区中考数学几何直观题型和考查的思想方法,提出培养学生抽象能力的“教—学—评”建议.
2 中考几何直观试题考查学生的思想方法案例分析
数学思想方法包括化归思想、函数思想、分类讨论思想、整体思想和形数结合思想等.借助几何直观试题,剖析中考试题考查的思想方法,通常按“观察—构造—推理”过程展开,此过程基本伴随有运算、建模和创新等活动.
2.1 考查学生的化归思想
化归转化思想能够帮助学生从看似杂乱无章的现象中抽象找到一般规律,把问题数学化,利用数学方法解决问题,是几何直观过渡到抽象能力的重要途径.
例1(2022·泰州)如图1所示的象棋棋盘中,各个小正方形的边长均为1,“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点的最短距离为.
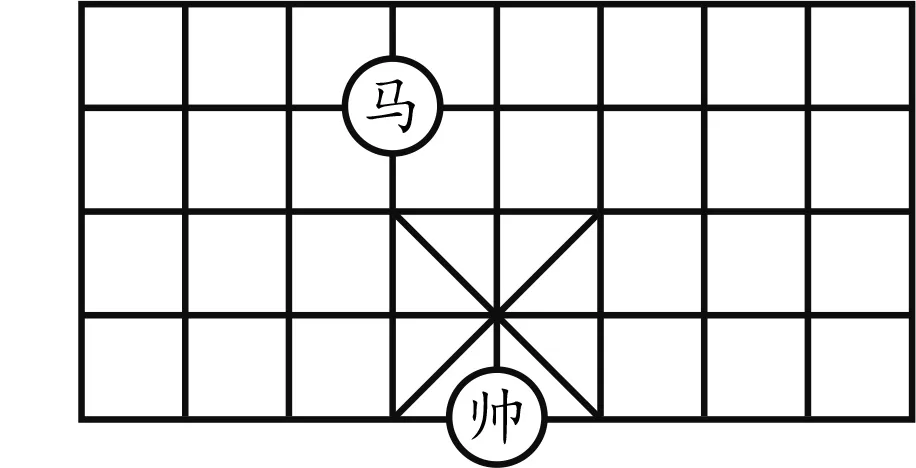
图1
构建直观模型
通过观察,建立“马走日”模型,尝试“马”的几种不同走法,作出预判.
推理解决问题
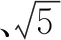
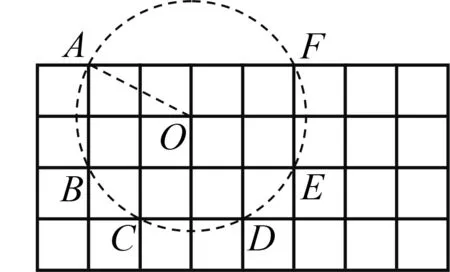
图2
例2(2022·绍兴)如图3,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,BC上的动点.下列四种说法:①存在无数个平行四边形MENF;②存在无数个矩形MENF;③存在无数个菱形MENF;④存在无数个正方形MENF.其中正确的说法个数是( ).
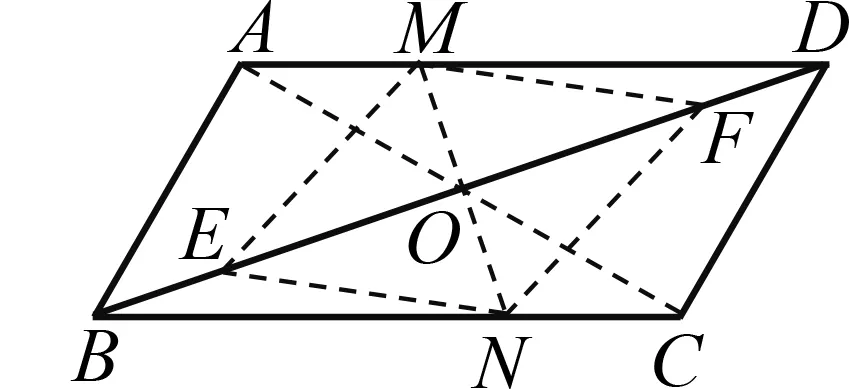
图3
A.1 B.2 C.3 D.4
构建直观模型
根据平行四边形对角线交点模型,画草图,作出预判.
推理解决问题
通过草图作出的判断只是“形似”,还要有一个数学化的过程.本例找出对角线的交点是关键.连结对角线AC交BD于点O,过点O作直线交边AD于点M,交边BC于点N.易证OE=OF,OM=ON,所以四边形MENF是平行四边形,答案A正确.
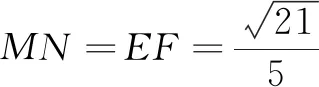
2.2 考查学生的函数思想
真正的知识,包括数学最为本质的知识,是来源于感性经验的,是通过直观得到的,抽象不能独立于人的思维而存在[3].建立在图形特征上的几何直观结论,要通过抽象的论证加以确认.
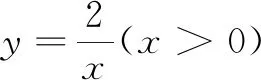

图4
建立形数联系
△AOB是等腰直角三角形,当直角边OA最小时,斜边OB也最小.
推理解决问题
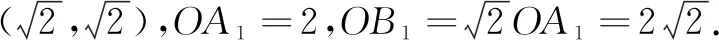
例4(2022·滨州)如 图5,正方形ABCD的对角线相交于点O,如果∠BOC绕点O按顺时针方向旋转,其两边分别与边AB,BC相交于点E,F,连结EF,那么点E在由B到A的过程中,线段EF的中点G经过的路线是( ).

图5
A.线段 B.圆弧 C.折线 D.波浪线
构建直观模型
建构“动点经过的路线”模型,通常操作是找出起点、终点和中间任意一点,通过观察三个点的位置判断其轨迹.∠BOC的旋转有两个特殊位置,起始位置点B与点E重合,此时点G为BC的中点I;结束位置点A与点E重合,此时点G为AB的中点H.连结IH,发现点G在线段IH上,从而初步判断中点G经过的路线为线段.
推理解决问题
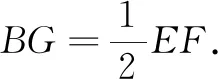
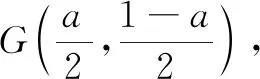

图6
2.3 考查学生的分类讨论思想
作图是形成直观想象的一种重要方法,图形特征越画越深入,数量关系越画越清楚,思路越画越清晰,思考越画越深入[4].通过作图,让学生借助几何直观感悟图形存在多种不同的情况,再从相似的图形中辨析“不同的结构”,提升学生的抽象能力.
例5(2022·绍兴)如图7,将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图7所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( ).
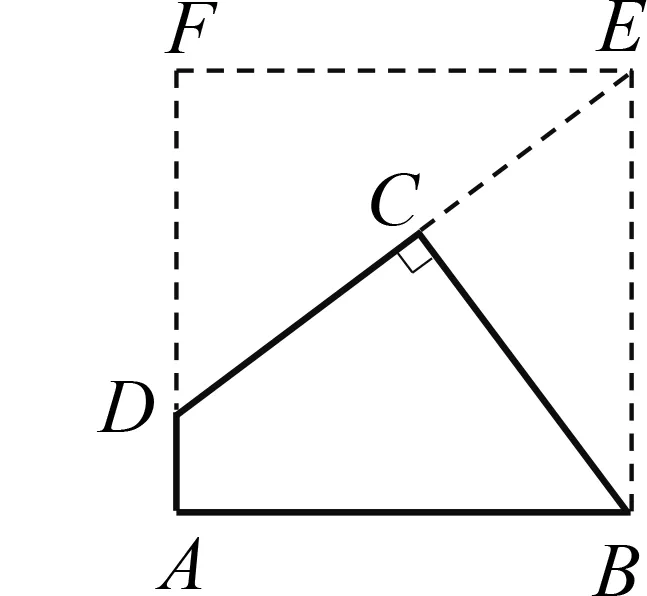
图7
构建直观模型
建构“相似直角三角形模型”,三角形是沿边CD,BC剪开的,且∠C=90°,尝试作图,还原尚未剪开的“原图”是解题关键.
推理解决问题
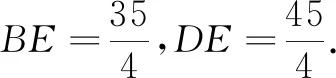
如图8,△HCD∽△BGH,通过计算可得DH=10,BH=15.答案A正确.
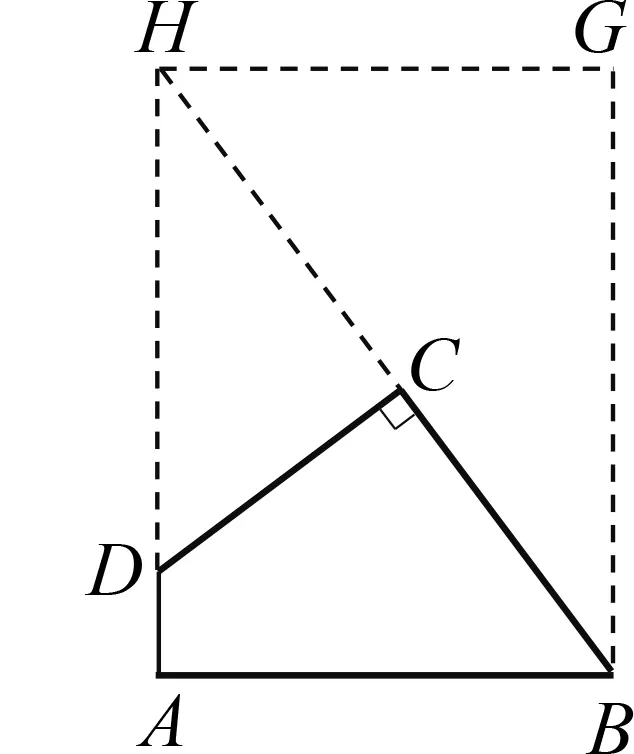
图8
2.4 考查学生的整体思想
借助几何直观认识图形,不能是盲人摸象,应该建立在图形总体特征的基础上,这样有利于更加深刻、全面地把握图形的特征,再通过抽象的代数运算进行确认.
例6(2022·宁波)将两张全等的矩形纸片和另两张全等的正方形纸片按如图9的方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等,若知道图中阴影部分的面积,则一定能求出( ).

图9
A.正方形纸片的面积
B.四边形EFGH的面积
C.△BEF的面积
D.△AEH的面积
建立形数联系
已知条件只有图形,没有矩形和正方形的边长,要判断四边形或三角形的面积,通性通法就是整体把握,设未知数判断四边形或三角形的面积的变化规律.
推理解决问题

2.5 考查学生的数形结合思想
“数缺形时少直觉,形少数时难入微.”数形结合思想是学生借助几何直观,进一步提升数学抽象能力的重要途径.
例7(2022·常州)如 图10,在四边形ABCD中, ∠A=∠ABC=90°,DB平分∠ADC,若AD=1,CD=3,则sin∠ABD=.
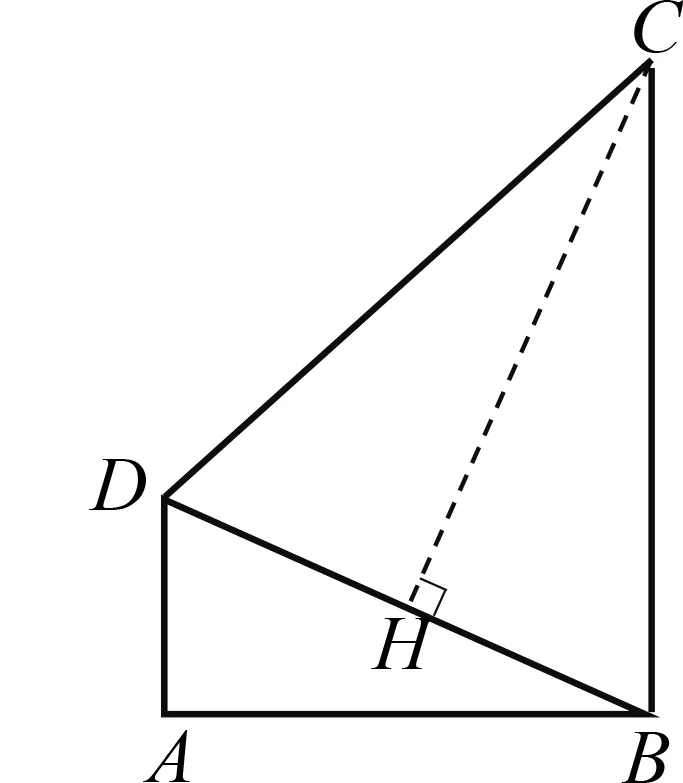
图10
建立形数联系
已知AD=1,要求∠ABD的正弦值,就需要求BD的大小.因为∠A+∠ABC=180°,所以AD∥BC,又因为∠ADB=∠BDC,所以∠DBC=∠BDC,DC=BC,添辅助线,过C点作CH⊥BD于H.
推理解决问题

例8(2022·宿迁) 如图11,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形面积平分,则直线l被正六边形所截的线段长是.

图11
构建直观模型
建构“正六边形的中心模型”,因为经过点M的直线l将正六边形面积平分,所以直线l经过正六边形的中心O.
推理解决问题

3 借助几何直观,培养抽象能力的“教—学—评”建议
“教—学—评”一致性的关键是要有清晰的目标.明确以培养几何直观为目标的教学策略,能促进学生从直观到抽象的提升.
3.1 在“教”中培养抽象能力
教学设计应体现逻辑的连贯性、思想的一致性、方法的普适性、思维的系统性,构建研究数学对象的基本路径[5].初中是学生感性思维上升到理性思维的重要转折阶段,这个阶段“教会”学生利用“眼观”把握图形,体会利用图形特征解题的优势;“教会”学生把生活问题转化为数学问题,体会“建构”直观模型的必要性,使形象思维过渡到抽象思维;“教会”学生结合图形进行“推理”,体会认识事物需要抽象的分析与论证的必要性.课前,教师要注重分析教学内容,明确哪些素材是培养学生几何直观、抽象能力的基本知识;课中,要制定培养学生几何直观、抽象能力的策略,让学生在掌握基本技能的同时,积累基本活动经验,从中体验几何直观的优越性;课后,要帮助学生梳理几何直观与抽象能力的联系,打通几何直观与抽象能力的通道,在数学基本思想的引领下让学生构建结构化的知识体系.通过几何直观和抽象能力相互作用,形成数学概念、性质、法则的方法与能力.
3.2 从“学”中提升抽象能力
数形结合活动是培养学生几何直观的有效途径[2].图形除自身具体的特征外,还包括图形的平移、旋转与轴对称等运动.学生“学会”在观察图形中发现问题,找到图形的特殊之处;“学会”从结论逆推提出问题,掌握演绎推理的方法;“学会”分析图形的基本特征找到解题方法,掌握逻辑推理的方法;“学会”数形结合,直观与推理相结合解决问题.这个过程中要鼓励学生大胆猜想、小心求证,鼓励学生在课堂上互动交流,从中“学会”从不同角度观察图形,“学会”从图形的特征挖掘有效信息,“学会”分析问题,“学会”提出自己感到困惑的问题,在倾听、思考与碰撞中提升抽象能力,思维由“零碎的认识”过渡到“整体地把握”,提升了抽象思维.学生以几何图形为介质,“学会”分析与综合、关系推理和质疑,提升了批判性思维;“学会”借助几何直观进行结构化、数学化处理,提升问题解决能力;“学会”联想迁移、类比化归,搭建起从直观到抽象的桥梁,提升了创造性思维;“学会”主动反醒,优化策略,提升了元认知能力.学生在构建问题的直观模型中,找到解决问题的策略,形成数形结合的能力,把握了数学的本质,提高了抽象能力.
3.3 在“评”中考查抽象能力
评价学生包括口头评价、书面评价和考试评价.口头评价主要在“教”的环节实施,课堂评价是一种过程性评价,评价学生是否利用几何直观准确认识图形、是否准确把握图形的特征、是否重视细化抽象过程、是否明确抽象的策略、是否掌握抽象的方法.书面评价主要在“学”的环节实现,评价学生是否准确运用图形特征、是否严密论证图形的结论、是否融汇贯通、是否增强了图形思维的意识.抽象能力水平主要在“考”的环节来反馈,抽象能力虽然不能直接观测,但抽象能力水平却能通过“数量关系”和“空间形式”这两个横向维度,以及“归纳与释义”“关联与建构”“拓展与普适”这三个纵向维度来测评.在抽象能力指标体系的指导下,教师能够制定更科学的策略,借助几何直观解决实际问题,让学生经历数学抽象的全过程,提升抽象思维的水平,引导学生从几何直观的角度对问题再认识、再思考.
“教—学—评”一体化评价的目的不仅在于检测教育教学效果,更重要的是发现教育教学过程中的问题,以及实施过程中的匹配度[6].通过评价中发现的问题,教师能及时发现教学中存在的问题,更好地调整教学策略,培养学生实现从感性到理性、从直观到抽象的跨越.
4 结语
几何直观是种意识,也是种技能与能力,更是种思维方式[7].以课标为引领,教师通过对中考试题的研究,有助于指导学生借助几何直观的思维方式把握问题的本质,明晰思维的路径.虽然学生的几何直观有先天的差异,但是通过后天的科学指导,学生的几何直观和其他关键能力将得到协同发展.

