章末复习课要重视回归教材与变式教学
——以《二元一次方程组》复习课为例*
刘东升 (江苏省南通市教育科学研究院 226600)
最近参加某地名师工作室组织的教研活动,听了一节《二元一次方程组》章末复习课.开课教师选了一套教辅资料配备的复习PPT,先练习了4道解二元一次方程组问题,然后是“链接中考”,和学生一起练习并讲评了3道二元一次方程组的应用问题.整节课基本上处于“一题接一题”“题题无联系”的刷题状态,是一节脱离教材的复习课.课后组织方也没有安排大家议课评课,只是由名师工作室领衔人对该课简要点评,高度评价了该教师的教学基本功及一些可圈可点的课堂生成细节.笔者课后对这节复习课进行了深入思考和再设计,现整理成文,供大家研讨.
1 七年级《二元一次方程组》章末复习教学设计
·活动1 从教材章前图问题出发

教学预设:除了代入、加减两种消元法之外,还可以启发学生用以下两种方法.
方法3:将②式变形为(x+y)+x=16,然后将①式直接代入可解出x.
方法4:将①式变形为(2x+y)+y=20,将②式直接代入也可解出y.
活动1主要是复习本章的教学重点——根据系数特点,灵活选择不同的消元策略解二元一次方程组.这个教学活动用时在5~8分钟为宜,可充分与学生对话,请学生上台讲解或演算解法.
·活动2 一起来“纠错”

教学预设:学生将2x+2y=16化简为x+y=8,这与另一方程x+y=10矛盾,故这个抄写的方程组是无解的.这里可以提醒链接如下的一道教材应用题:
某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入393元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
教学预设:学生先设出未知数,列出方程组,再简要变形后得到矛盾,所列方程组无解,说明记录有误.在此基础上,再给出问题3,训练整体变形求解.讲评之后,如果学情较好,教师可从二元一次方程组一般形式的角度,讨论各项系数特点与方程组解的情况.
问题3有甲、乙、丙三种货物,若购甲货物2件,乙货物4件,丙货物1件,共需90元;若购甲货物4件,乙货物10件,丙货物1件共需110元.若甲、乙、丙三种货物各购1件,共需多少元?
教学预设:出示该题之后,考虑本课主要不是训练解决实际问题,所以为了节约教学用时,可在PPT上虚拟小虎同学对这道题的如下初步思考:
小虎同学设甲1件需x元,乙1件需y元,丙1件需z元,根据题意,列出三元一次方程组后发现,这个方程组中有3个未知数,却只有两个方程,小虎认为题目有错.
请同学帮助分析一下,这道题目是否有错漏?难道也无法求解吗?
教学预设:问题3有多种整体变形、代入消元的方法,教学时注意根据学情相机追问有没有不同的方法,将学生的思维引向深入,这也与开课阶段复习二元一次方程组不同解法形成一种呼应.整体来说,活动2教学用时要控制在12~15分钟.
·活动3 含参数的方程组问题
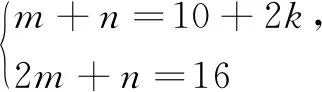
(1)用含k的式子表示m,n;
(2)设平面直角坐标系xOy中,点P(m,n)到x轴的距离是到y轴距离的两倍,求k的值.

教学预设:活动3教学用时控制在12~15分钟为宜.解后回顾反思时,要让学生对比变式问题、不同解法之间的联系.这个回顾反思非常重要,是帮助学生学会反思、学会看清不同问题的“一致性”的有效活动,有利于学生今后遇到陌生问题时能及时进行“等价转换”.
·活动4 课堂小结,布置作业
小结问题1:开课阶段主要复习了二元一次方程组的不同解法.现在你对二元一次方程组的消元法有了哪些新的认识或理解?
小结问题2:本课中有些习题的解法很有趣,体现了“少算多思”的特点.哪道习题或解法给你留下了深刻的印象?请和同学们交流一下.
布置作业:
1.解方程组
立意解读:该方程组中的第1个方程不宜直接去分母、移项、合并这样去化简、整理,而应该着眼于整体,反复运用乘积为1或-1的性质整体解读,达到化繁为简的变形目标.

2 关于章末复习课的教学思考
2.1 章末复习课要体现回归教材
教材在章末小结时常常会给出一个知识框架图和一些复习要点,然后就是一组复习题.教师在新授课期间或课外作业已布置给学生练习过,待到章末复习时,总感觉教材上没有内容可以复习选用.这是一种误解,认为章末复习课只要关注教材上的章末小结那几页内容.事实上,对章末复习课,教师要再次研究整章教材内容,从章前图到章末小结都要细致查阅、研究,再认识、再理解、再体会,往往能发现教材编写者的良苦用心,也就能抓住教材上的重点内容、经典问题,并将其作为复习课的重要学材进行选编、开发和运用.可以发现,上文复习课例中,从开课阶段的问题到复习进程中链接的实际问题或变式问题都与教材密切相关,让学生感受到章末复习课就是对教材上很多问题的“再理解”与“再探究”.
2.2 章末复习课要重视一题多解
从一些章末复习课的听课情况来看,课堂中习题容量偏大,往往会导致一些教学内容来不及讲解.这样一来,有些值得开展深度讲评的例习题就没有跟进必要的追问,包括一题多解的研究,使得学生对这些问题的接触成为“入宝山而空回”.笔者以为,适当减少课堂容量,通过必要的一题多解,既能减轻课堂上学生忙于刷题导致的学习倦怠,也能帮助学生从不同角度认识一些典型习题或解法.单墫先生曾说:“一道题,怎样才能找到解法?这是一个很难说清楚的事情.但如果解完题以后,回顾一下,或许可以总结出一些规律性的东西,这些东西有助于我们今后找到解题的方法.琢磨已有的解法,也能学到一些解题的方法.”[1]在上文课例中,开课阶段我们就让学生运用不同方法求一个简单的二元一次方程组,这种一题多解看似价值不大,但一些解法中的整体变形、代入化简,却为后续较复杂问题的解决提出了解题思路或求解方法.
2.3 章末复习课要加强变式教学
变式教学是很多教师开展解题教学时都积极实践的一种有效的教学方式.在复习课中,对例习题进行即时变式或拓展,帮助学生举一反三、触类旁通,也就追求了适合学生的教学深度[2].上文课例中,我们从不同角度积极实践变式教学,比如问题2和问题4的题干都可以看成是由问题1变式而来,让学生感受到不同复习活动之间的联系,追求较好的“转场”效果.而问题2或问题4下面的系列问题也都紧密联系、变式推进,有些虽然看似“形异”,但是它们从解题思想层面上却体现着整体处理策略,实际也是一类“质同”问题,类似的变式教学对于训练学生识别“等价问题”往往会起到很好的示范作用.

