数列解密同构显 课本一隅题根隐
巨小鹏 黄龙海
(陕西省汉中市龙岗学校)
解题的目的在于化繁为简,以此理解数学的本质.作者曾对同构法在函数和解析几何中的应用做了归纳分析后,数列中的同构思想解题也在课本中找到了其题根题源,特别是对一阶递推数列和二阶递推数列问题做以分析,寻找其规律,揭示其本质.
1.平凡见奇生面开——真题呈现
【例1】(2020·全国Ⅲ卷理·17)设数列{an}满足a1=3,an+1=3an-4n.计算a2,a3,猜想{an}的通项公式并加以证明.
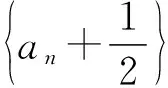
2.源头活水清如许——课本寻根
陈景润先生曾谈起数学解题时说:“题有千变,贵在有根”.以题根为源展开探究,旨在找到破题方向,抓住解题思维入口,通过变式拓展理解解题“大道至简”的解题模式,理解数学概念和定理(公式)的本质,找到题根题源,就找到问题的底层逻辑,以此展开思维继续探究.
题源1(苏教版(新版)高中数学选择性必修一P163问题探究)若数列{an}满足:a1=1,a2=5,对任意的n∈N*,都有an+2=4an+1-4an,求an的表达式.
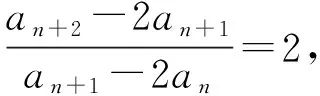
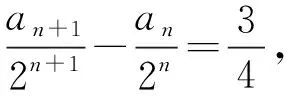
请仿照上面的解法,思考:已知数列{an}满足:a1=1,a2=1,对任意的n∈N*,都有an+2=an+1-an,求an的表达式.(解析略)
题源2(苏教版(新版)高中数学选择性必修一P168第16题探究题)已知数列{an}满足:a1=1,对任意的n∈N*,都有an+1=2an+1,求an的通项公式.
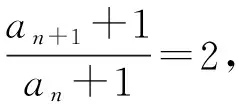
3.鸳鸯绣出教君看——同构法问题解答
【例1解析】解法一:由题意可得a2=3a1-4=9-4=5,a3=3a2-8=15-8=7.猜想an=2n+1,证明:由a1=3,a2=5得a2-a1=2.因为an+1=3an-4n,an=3an-1-4(n-1)(n≥2),两式相减得an+1-an=3(an-an-1)-4,令bn=an+1-an,且b1=2,所以bn=3bn-1-4,两边同时减去2,得bn-2=3(bn-1-2),且b1-2=0,所以bn-2=0,即an+1-an=2.又a2-a1=2,所以数列{an}是首项为3,公差为2的等差数列,所以an=2n+1.
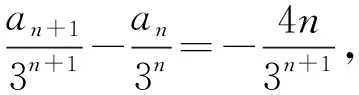
解法三:由题意可得a2=3a1-4=5,a3=3a2-8=7,猜想an=2n+1.证明:由于an+1=3an-4n,所以可设an+1+λ(n+1)+μ=3(an+λn+μ),其中λ,μ为常数,整理得an+1=3an+2λn+2μ-λ,故2λ=-4,2μ-λ=0,解得λ=-2,μ=-1,所以an+1-2(n+1)-1=3(an-2n-1)=…=3n(a1-2×1-1).又a1-3=0,所以{an-2n-1}是各项均为0的常数列,故an-2n-1=0,即an=2n+1.
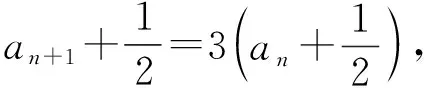
从两个高考例题和题根中可以看出,解题过程中通过引导和同化,以顺应学生的思维层次和知识结构,让学生从观察到变形,将条件进行等价转化,化成结构形式相同的方程,然后构造出等差(比)数列,从而利用熟悉的等差(比)数列定义或者性质解决问题,起到化繁为简的目的,我们将这种方法称为“同构法”.
4.悉数金针度与人——数列中应用举例揭规律
4.1方程中数列同构问题
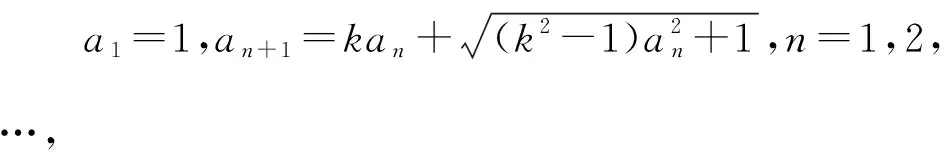
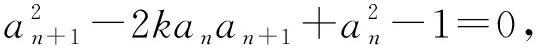
4.2递推数列中同构问题
类型一an+1=pan+q型
an+1=pan+q构造同构式an+1+m=p(an+m).例如题源2.
类型二an+1=pan+an+q型
an+1=pan+an+q构造同构式an+1+A(n+1)+B=p(an+An+B).
【例4】已知数列{an}中,a1=3,且满足an+1=an+2n+2,bn=an-n2(n∈N*).证明:数列{bn}是等差数列,并求{bn}的通项公式.
【解析】证明:因为an+1=an+2n+2,所以an+1-(n+1)2=an-n2+1,故bn+1-bn=1,所以数列{bn}是等差数列,且公差为1.又b1=a1-1=2,故bn=2+(n-1)=n+1.
类型三an+1=pan+rpn+1型
an+1=pan+rpn+1型方法参考题源1.
类型四an+1=pan+rqn+1型


类型五an+1=manr型
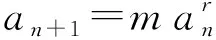
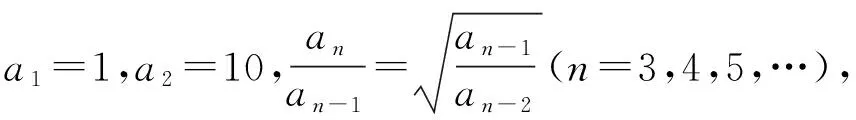
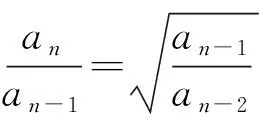
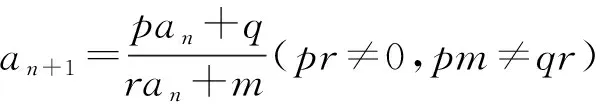

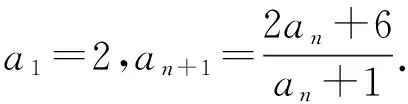
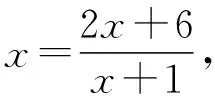
类型七an+2=pan+1+qan型
an+2=pan+1+qan构造同构式an+2-san+1=t(an+1-san),或者求出特征方程x2-px-q=0,特征根是α,β,若α≠β,则an=Aαn+Bβn,若α=β,则an=(An+B)αn,其中A,B为常数,根据a1,a2的值,建立方程组求出常数A,B,即得an.
【例7】已知数列{an}满足a1=2,a2=8,an+2=4an+1-3an.求{an}的通项公式.
【解析】解法一:方法如题源1得数列通项an=3n-1.
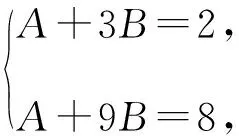
类型八an+2=pan+1+qan+t型
an+2=pan+1+qan+t构造等差数列即可.
【例8】数列{an}满足a1=1,a2=2,an+2=2an+1-an+2.设bn=an+1-an,证明{bn}是等差数列.
【解析】证明:由an+2=2an+1-an+2,得an+2-an+1=an+1-an+2,即bn+1=bn+2.
又b1=1,所以数列{bn}是首项为1,公差为2的等差数列.
【评注】以上类型通过化归与转化为已知熟悉的形式解决问题,除了同构转化还利用了不动点法和特征根法解决问题,它们也具有同构思想.


