例析求分式值的几种常用方法
甘肃省白银市白银区武川新村学校
王花香
分式的计算是“认识分式”这一章中的重点,而求分式的值是分式的计算中的重点.由此可见,掌握求分式的值的方法,对提高学生本章知识点的掌握程度和应用能力具有积极意义.所以,本文中在举例分析的基础上,利用举一反三或变式等方法,呈现求分式的值的几种常用方法,以期帮助一线教师不断提高课堂教学效率.
通过对近几年各地中考数学试卷的分类整理发现,求分式的值多以解答题形式出现,在某些省市区的试卷中也会以选择、填空题的形式出现.下面,笔者采用例题分析的方式展现求分式的值的几种方法.
1 参数法
参数法是解决求分式的值这类问题时最常用的方法,掌握这种方法,也就能解决大部分求分式的值的问题[1].

分析:这道题中的条件以等比的形式出现,那么可以假设该比的比值为k,把待求式转化为关于k的代数式的值.
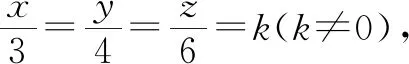
x=3k,y=4k,z=6k.

方法总结:参数法指的是在解题过程中,通过适当引入一些与题目研究的数学对象发生联系的新变量(参数),以此作为媒介,再进行分析和综合,从而解决问题[2].此外,运用参数法需注意两个问题:
第一,所设参数应保证不为零;
第二,不要受到引入的参数的干扰,因为最终该参数会消去.
在例1中,通过引入参数k,将x,y,z均用含k的代数式表示出来,最后消去参数k,求得结果.
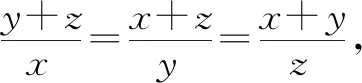

y+z=kx,
①
x+z=ky,
②
x+y=kz.
③
于是,由①+②+③,可得
y+z+x+z+x+y=kx+ky+kz,
2(x+y+z)=k(x+y+z).
因为x+y+z≠0,所以k=2.

2 两头凑法
所谓两头凑法,其实就是观察条件的特点思考所求分式需要怎样的信息,或观察所求分式的特点思考需要怎样的条件[3].
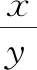
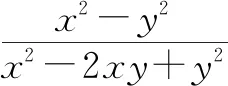
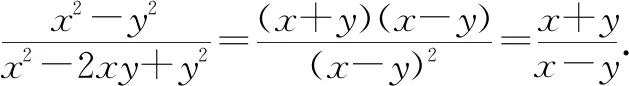
④
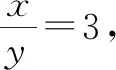
将x=3y代入④,得
解法2:由于xy≠0,则根据分式的基本性质,将分式的分子、分母同时除以xy,得
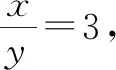
所以,由⑤得
方法总结:解决分式的求值问题,最有效的方法是将题目已知条件和所求问题一同考虑.根据这一思路,首先要考虑条件能为所求问题提供什么有价值的信息,然后考虑所求问题需要条件能提供什么有效信息,这就是两头凑法[4].
需注意的是,在变形已知条件时,应该使变形所得到的式子在所求的式子中可用,如解法1;或者,变形所求的式子时,应该与已知条件有明显的、直接的联系,如解法2.
3 整体法
整体法和“认识分式”这一章中蕴含的整体思想有关联.

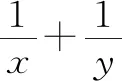

x+y=5xy.
⑥

所以将⑥代入⑦中,得

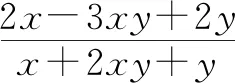
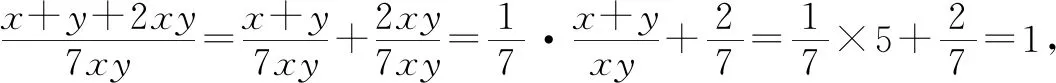
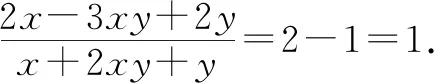
解法3:由题意可知x≠0,y≠0,所以xy≠0.
将分式的分子、分母同时除以xy,可得


总而言之,求分式的值的方法非常多.本文中所例举的参数法、两头凑法和整体法是几种比较常用的方法.这几种方法灵活性较强,一线数学教师应抓住机会构建高效课堂,让学生在这样的课堂中得到较充分的训练.

