最简分式易错点及避错策略分析
甘肃省平凉市崆峒区广成学校
周义武
根据目前的实际教学发现,学生在最简分式这一知识点上的掌握情况不容乐观,时常会出现一些错误.所以,笔者认为有必要在阐述其相关内容的基础上,对常见错误类型及其错因进行深入分析,并提出相应的解决策略.
1 最简分式相关概念
当分式的分子和分母没有公因式时,这样的分式称为最简分式.在化简分式的过程中,通常要让结果成为最简分式或整式[1].要准确理解最简分式的概念,需从以下几点入手:
第一,分子和分母中没有公因式,是判断分式为最简分式的关键.由此可见,最简分式的化简与分式约分中的公因式有关.
第二,分式及分式的运算结果,一定是最简分式或整式.所以,在运算的最后一定要记住化简[2].
例1下列选项中是最简分式的是( ).
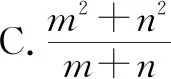
分析:一个分式经过约分得到的化简结果就是最简分式,所以最简分式的分子与分母不再存在公因式,即分子分母不能再约分.若分子和分母都为单项式,那么它们可直接约分得到最简分式,如A选项.若分子分母中有多项式的,应先因式分解,然后再约分,如B,D选项.综上所述,C选项是最简分式,因为m2+n2≠(m+n)2,所以分子分母没有公因式.
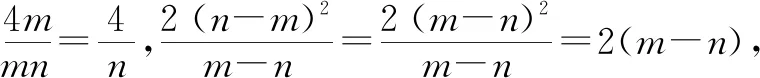
故选答案:C.
例2将下列各分式化简:
分析:约分作为获得最简分式的直接方法,对学生牢固掌握最简分式来说非常关键.约分首先要找准分子分母的公因式,方法是——系数取最大公约数,字母(或式)取分子分母中都出现的,次数取最低.
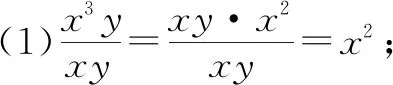
2 错题例析
结合一线实际教学情况,学生在以下几方面容易出错.
2.1 约分不彻底
例3化简下列分式:
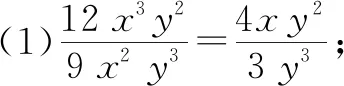
分析:本题的解题过程出现了约分不彻底的情况,是学生将分式化成最简分式时常见的错误,其根源就在于没有牢固掌握找公因式的方法.

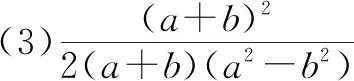
2.2 公式应用错误
例4化简下列分式:
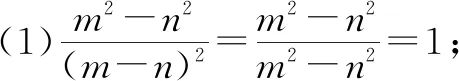

=x+4.
分析:将分式化成最简分式时,一定要注意公式是否应用正确.学生将(1)中的(m-n)2看成了m2-n2,这也是学生经常出现的错误.(2)中既没有将4-x2根据平方差公式因式分解,又出现了代数式的变形处理错误.
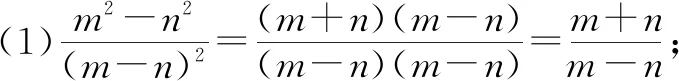

2.3 约分后漏项

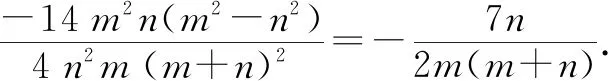
分析:像这种字母多、指数多的约分问题学生极易出错,因为他们对分子分母约分后各剩下哪些部分不够清楚,在比较复杂的情况下极易混淆.

2.4 不先因式分解而直接消去相同的字母
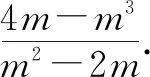
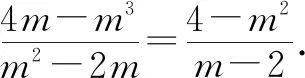
分析:在一些后进生当中,他们时常会将分子分母中相同的字母直接消去,而不因式分解.这种做法是容易出现错误的.

=-m-2.
3 避错策略
想要避免以上这些错误,笔者认为除了养成仔细检查的习惯外,还需从以下几个方面着手.
其次,巩固平方差公式和完全平方公式仍非常重要[3].除了理解和掌握“(a+b)(a-b)=a2-b2”,“(a±b)2=a2±2ab+b2”外,还需将其中的a,b转换成多项式进行灵活变换,如(2a+3b)(2a-3b)=(2a)2-(3b)2=4a2-9b2,[(x+1)±(x-1)]2=(x+1)2±2(x+1)(x-1)+(x-1)2等.如此一来,对培养学生的数感也非常有帮助.在这里,笔者再次提醒a2+b2≠(a+b)2.
再次,针对约分后漏项的错误,笔者的做法是在训练时使用不同颜色的笔消去相应部分,然后对分子、分母从左到右逐项查找剩下的部分,再核对一遍后才书写化简后的结果.这里的关键步骤是“对分子、分母从左到右逐项查找剩下的部分”,希望教师教学和学生学习中都注意该点.
最后,针对不经过因式分解而直接消去这种易出错的做法,需要教师耐心讲解,一旦这部分学生解决了这一问题,他们的化简能力将大大提升.
综上所述,作为分式中比较基础的一个知识点,化简分式依然存在许多易错点.作为一线数学教师,首先要善于观察和收集学生的错题并进行分类和分析,然后探索一些有效的策略帮助学生避错[4].作为一名初中生,更需要在平时的学习与训练中养成良好的学习习惯,从上文中提出的四点策略出发尝试改变这个知识点中存在的错误.

