精讲习题注重转化技巧 提高思维减轻作业负担

［摘  要］ 文章剖析了小学生解决问题能力薄弱的原因，提出在教学实践中要关注学生思维角度的转化，即从情境、条件、句式、数量关系这四个维度进行转换，加强学生数学解题技巧的训练，提升学生的解题能力，为学生减负提供现实抓手。

［关键词］ 数学解题；转换；解题能力；减负

解决问题是小学数学教学的重点与难点，但现实中有部分学生在解决综合性强、思维性强的实际问题时总是“毫无头绪”和感到苦恼。究竟是什么原因导致了学生思维受阻呢？笔者认为，主要原因是学生思维角度的错位，没有领悟这类问题的思维特征与基本思想，探寻不到条件与条件、条件与问题间的联系，对题目中的关键性条件与关系不能准确地转化。针对上述现象，笔者在教学实践中着重关注学生思维角度的转化，加强学生数学解题技巧的训练，收到了良好的教学效果。

一、分析情境，转化成熟悉的情境，让学生在顿悟中解题

在做題时，学生常常觉得每一道题目都很陌生；而在讲评时，教师稍做点拨学生就觉得非常熟悉。这是为什么呢？事实上是因为编题者所设计的陌生情境让学生无法弄清题目的条件。因此，在教学中教师需要引导学生深入分析情境和学会将陌生情境巧妙地转化为熟悉情境，才能让学生看清问题的本质，在顿悟中解题和提升解题能力。

例1  星期五，全校卫生清理日，三年级（3）班开始打扫卫生，学生带来了抹布擦洗瓷砖（男女生都有）。若男女生都擦洗，每个人要擦洗6块；若让所有女生擦洗，每个人要擦洗18块。若只让所有男生擦洗，每个男生要完成多少块？

分析：初看题目，不少学生会认为这是一道整数应用题，认真读题后却发现本题条件不清楚，比如总人数不知、瓷砖数量不知、男生人数不知、女生人数也不知，这些“不知”让学生深感棘手。此时，教师可以点拨学生转化题目的情境，试着将其转化为数量关系相同的问题来探寻解决问题的思路。

这里，教师鼓励学生变陌生为熟悉，将一道陌生情境问题改编成一道典型的工程问题，使得后续的分析和解题变得简单，在教会学生解题技巧的同时培养了学生“化生为熟”的思维品质。

二、分析条件，转化成简单的关系，探寻解题的突破口

解决问题的过程是不断去变化题目的过程。转化思想就是转化观察的角度、转化思考的方式、转化表达的语言、转化处理的观点，在朝着利于问题解决的方向不断转化的过程中，将条件间的关系转化得更加简单，直至探寻到解决问题的突破口。教学中，不少学生常常抱怨分数的实际应用问题条件繁杂，不易解决，在练习中频频出错。尤其是面对条件中“1”分率单位不同时，学生往往会思维卡壳，完全找不到解决问题的入口。

因此在教学中教师应教会学生分析条件，找寻到不变的量来统一条件中的单位“1”，这样就可以将复杂的条件关系转化成简单的关系，以获得解决问题的思路。

分析：读题后，发现例2中有两个条件中包含分率，分别以芳芳和红红带的钱为单位“1”，而当芳芳借了红红60元之后，两个人身上的钱就都有了变化，使得学生的解题难度又增加了。该如何解决呢？显然，根据上述条件，教师需提醒学生解决本题时要牢牢把握其中不变的量，是什么呢？再次读题后，学生可以得出一直不变的量是“红红与芳芳两人钱的总数”。探究到此，只需要转化条件就可以让问题迎刃而解了。

就这样，师生通过深入分析条件，把握住条件中不变的量，进一步完成由复杂到简单的转化，在不改变题意的情况下让变化的量转化为一定的量，让问题变得简单易懂，让解题事半功倍。

三、分析句式，转化成相同的句式，让问题本质明朗化

可见，分数实际应用问题数量关系复杂，尤其是当单位“1”各不相同时学生理解起来难度较大。但借助于分析句式，并将其转化为相同的句式，可以使得问题本质明朗化，让学生轻松解题。

四、分析数量关系，转化成直观的图形，让问题轻松获解

一般来说，若能将一个特定问题转化为一个图形，则可以整体把握住解决问题的思路，从而创造性地获得解决问题的解法，这即为“数形结合”思想。小学生的抽象思维并不发达，在解决问题中，倘若能以形象性的图形作为引线，则可以让抽象的问题变得直观，让问题轻松获解。因此，在解题中，教师需指导学生分析数量关系，合理利用数形结合将抽象的数量关系转化为直观的图形，去简化解题过程，达到良好的解题效果。

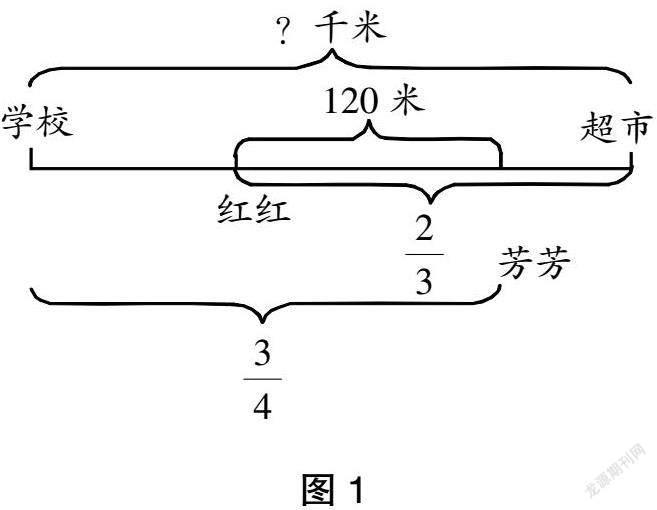
分析：本例是一道典型的行程问题，其中关键点有“同时”“两地”“相向”。深入分析这些关键条件，可以得出芳芳和红红相遇后继续向前行驶且都没有到达目的地。事实上，此类题目学生很少遇到，自然无法理清题目中复杂的数量关系，陷入了解题困境。而此时若能作出线段图，则可以直观探寻到120米的对应分率，让复杂的数量关系变得直观形象，使问题轻松获解。

于是，教师点拨学生作出如图1所示的线段图，这样一来，题目中的数量关系变得一目了然，学生可以很快从多个角度入手列出算式，获得答案“288米”。

“数”抽象概括，“形”形象具体。上例中，教师从小学生的思维特征入手，引导学生巧妙利用数形结合，将抽象的数量关系转化为直观的线段图，充分发挥直观对抽象的作用，触及问题的本质，方便问题的分析与解决。

总之，数学解决问题虽然情境复杂、综合性强，但绝大多数题目有法可依、有路可循。在日常教学中，教师需要一以贯之地培养学生的转化意识，强调转化情境、转化条件、转化句式、转化数量关系。这样可以让解题“峰回路转”，能够训练和培养学生解决问题的技巧，提升和发展学生的解题能力和思维能力，从而切实减轻学生数学作业负担。

作者简介：唐海林（1984—），中小学一级教师，从事小学数学教学工作。