“归纳推理”在数学教学实践中的应用研究

［摘  要］ 归纳推理作為逻辑推理的重要组成部分，在小学数学的教学设计、教学活动实施以及解题活动中都有重要意义。文章从归纳推理的理论基础出发，着重梳理了归纳推理在小学数学教学中的实施目标，并提出在教学中的具体实施措施。

［关键词］ 归纳推理；推理；目标

数学逻辑推理能力被新课标作为六大核心素养之一，不论在教学设计、教学活动实施还是解题中都有重要意义。归纳推理能力对小学生解决数学问题有着重要的作用。笔者着眼于小学数学课堂教学，基于大量的教学实践来探讨归纳推理能力的内涵与实际应用价值。

一、理论基础

逻辑推理从结构出发，可以分为演绎推理、归纳推理和溯因推理三种。其中，演绎推理是指从已知的定理、定义或确定的规则出发，从逻辑推理的程序进行计算与证明的过程，包括从一般到特殊与从特殊到一般两类，又被称为唯一能获得确定结论的推理方式。归纳推理主要是指在实践中寻找问题间存在的规律，并通过猜想获得一般模式，从而提出一般性结论的过程［１］。

为了让人们能区分出这三类推理方法，皮尔逊借助法则、实例与结论三个要素，对每种类型的推理分别进行了描述。法则是指一种情况发生，另一种情况必然会出现的命题；实例指在一定条件下，观察事物的特点与联系；结论与实例类似，但又包含法则。

不同类型的推理，其着重点有着一定的区别。法则为演绎推理的核心，而实例为归纳推理的基础，溯因推理则借助相应的法则与结论来解释实例。康纳尔（Conner）等人又进一步将该理论与图尔明的一般论证结合在一起，更加明晰了各种类型推理的关系，充分展示了法则、实例与结论在各个推理类型中的角色。

二、实施措施

（一）过程要素分析

归纳推理的过程要素主要有：①研究数学对象的性质特征与对象之间的关系；②认识数学对象之间的异同点；③建立概念、运算法则，发现研究对象的性质与规律等；④用精准的文字、语言符号清晰地表达归纳过程。

（二）实施目标梳理

任何能力的培养都需遵循由浅入深、循序渐进的过程，想要培养学生的归纳推理能力，必须从学生的实际出发，符合学生的认知发展规律。实践证明，归纳推理的实施一般遵循以下四个阶段：

1. 前归纳阶段

此阶段主要是培养学生的观察习惯，让学生在观察与分析中积累一定的数学经验，适用于一年级学生的教学。其过程为：学生经历数学活动，从中积累一定的经验，对研究对象产生直观或感性认识；当学生再次遇到类似的问题情境时，就会激活认知，形成自己的判断。

案例1  “加法交换律”的教学

学生从自己的认知经验出发，能计算类似于“7+5=12、5+7=12”之类的题。虽然学生还不了解“加法交换律”，但在反复的练习训练中，仍然能形成“两个加数的位置发生交换，所获得的结论还是一样”的隐性认知经验。这个简单的模式识别式的推理，就属于潜意识中的归纳推理前归纳阶段。

前归纳阶段应结合学生的认知特征，以具体的生活实物、数量与图形为载体，让学生在直观感知中获得相应的认知，从而达成以下几个目标：①初步学会观察方法，形成良好的观察习惯；②学会简单的比较与分析，发现所观察对象的异同点，学会简单的分类，切身感知规律的含义；③积累相应的比较、分析、分类的经验。

2. 初级阶段

该阶段主要培养学生分类与探寻规律的能力，主要适用于二三年级学生的教学。学生在前归纳阶段的基础上，进行简单、系统的归纳推理。然后结合数的认识、几何图形的学习，在操作、观察中对研究对象进行比较、分析，从而发现事物之间的异同点。从内容上来看，主要侧重于图形与数量性质等方面的探究，利用枚举法推理出相应的结论，并能用恰当的语言符号来表达。

案例2  “有余数的除法”的教学

教学时，教师要引导学生在分发物品的活动中，发现“有余数”的现象，从而建立“余数”与“有余数除法”的概念。教学活动中，教师可鼓励学生摆一摆，学会对除法算式分类：有余数和没有余数两大类，通过归纳发现4根小棒可以摆出一个正方形，而无法摆成正方形的小棒分别有1、2、3根，据此发现“余数＜除数”的规律。

初级阶段应达到的目标为：①根据标准进行合理分类；②对规律形成基本认识，能提出简单的猜想，并能用语言符号进行表示；③积累互动经验，为完善推理奠定基础。

3. 完善阶段

归纳推理的完善阶段即检验评估与反例验证阶段，与四五年级学生的认知相匹配。此阶段的学生已经有了一定的推理经验，教师利用数形结合思维，能进一步强化学生对数学现象的观察、分类、分析与比较等能力，让学生对自身所猜想的结论进行客观的评估，且能用反例法来论证错误结论。

学生在此阶段既关注研究对象的数量或图形的性质等，又对数量或图形之间的关系有了进一步的探索。而教师应引导学生在感知数学对象的表面特征上，通过思维加工其本质、内在特征等，并能用枚举法获得相应的结论，用精准的语言或符号进行表达。

案例3  “三角形三边关系”的教学

教学时，教师提供一些长短不一的小棒，让学生任选3根摆成三角形的形状，并对摆放过程进行思考与分析，在比较中形成初步猜想。在此基础上，鼓励学生任意画三角形，让学生在“量、算”的过程中验证自己的猜想，并自主获得以下结论：任意三角形的任意两边长度之和，必须大于第三条边。

教师可带领学生一起探究：三角形的两边之和为什么不能等于或小于第三条边呢？鼓励学生应用反例进行验证，以完善自己的认知。

归纳推理的完善阶段需要达到以下目标：①加强学生应用枚举归纳法获得猜想，尤其要学会应用这种方法促进运算法则与各种规律的建构；②错误猜想的应用，让学生感知枚举归纳法所获得的猜想或结论具有或然性，验证猜想是必不可少的环节，并学会运用反例法来推翻错误的猜想。

4. 前演绎阶段

此阶段是學生明白“是什么”“为什么”的环节，适用于六年级学生的教学。在该阶段，教师应引导学生应用数形结合思想，深入观察、比较、分类、分析活动过程，形成相应的猜想或结论，并确定猜想的合理性与相应的数学意义，也就是做到知其然且知其所以然。

案例4  “长方体的体积”的计算公式

活动1：教师组织学生进行小组合作学习，每个小组用若干个1cm3的正方体自主摆出各种各样的长方体，并绘制表格，记录相应的数据。

活动2：要求学生用小正方体摆放出指定尺寸的长方体。

根据两次探究活动所形成的数据进行归纳推理，鼓励学生自主分析出长方体体积计算公式。分析过程中，学生应用了枚举归纳法，自主获得了该公式“是什么”。对于小学高年级的学生而言，知道“是什么”还远远不够，只有发现长方体长、宽、高之间的内在联系与计算公式的“为什么”才算完成教学任务。

鉴于此，教师可适当地增加演绎推理的教学，引导学生用科学归纳法理解1cm3为单位体积，将一个大长方体分割成一个个1cm3的小正方体，则为该长方体的体积。如此可强化学生对长方体体积的认识，让学生从真正意义上理解该公式的内涵。

归纳推理的前演绎阶段应达到的目标为：能用枚举归纳法，促进运算规律与发展的形成，适当增加演绎成分；引入科学归纳法，让学生通过个例的分析，发现问题的因果联系，自主解释结论或猜想的过程，达到科学归纳的层次。枚举归纳法要获得“是什么”，科学归纳推理要达到“为什么”的层次。

纵观以上四个阶段，它们遵循由浅入深、循序渐进、逐渐深入的过程，而且四者是相辅相成、不可分割的，它们是互相推进的关系。结合学生智力与认知发展规律，在此阶段实施归纳推理目标，应有明显的层次性与阶梯性，为学生形成完整的归纳推理能力奠定基础。

三、实施策略

（一）明确推理目标，获得猜想方向

数学学科具有一定的复杂性与抽象性，对学生的想象力与逻辑推理能力要求较高。教学时，教师应引导学生明确推理目标，让学生能从自己的直觉出发，结合自身的认知经验，进行大胆猜想、推测与归纳。因此，目标是教学活动的“灯塔”，学生在目标的指引下，会迈出敢想、会想的第一步；同时，教师还要根据学生思维的实际情况，引导学生从问题的各个维度去猜想，获得更多、更完善的结论。

案例5  “积的变化规律”的教学

计算下列各式，并分析比较各式积的变化规律。

20×3=60；

20×（3×2）=（  ）；

20×（3×10）=（  ）；

（20×4）×3=（  ）。

教师如果直接提出：“通过以上计算，你发现了什么？”学生一般都会通过观察，提出结论：乘数×2，积也×2；乘数×10，积也×10等。这个结论没什么问题，但拘泥在具体数值上，学生就达不到对一般积的变化规律的认识。

因此，教师在学生观察之前，应提出一个明确的归纳推理方向。比如：“大家观察以上算式，说说两个乘数分别发生了怎样的变化？当一个乘数不变时，另一个乘数与几相乘积会发生怎样的改变？”

这样，学生自然而然地朝教师所提供的方向去猜想，所获得的结论就带有明确的目标性。当然，教师在预设目标时，并没有硬性的规定，而是一种引导，让学生感知规律的存在。值得注意的是，教师不能将自己的思路强加给学生，而要从启发的角度，引导学生进行全方位的思考。

（二）引导自主归纳，感知推理过程

史宁中教授认为归纳推理是一种智慧，这种智慧并非表现在经验结果上，它体现在思考与经验过程中［２］。归纳其实是学习者的直觉与逻辑思维交织互动的一个过程，因此有着一定的规律性。学生只有掌握了归纳推理的一般思维步骤，才能明晰自己接下来应该思考什么。

归纳推理的思维过程，主要遵循以下几个步骤：①综合分析素材；②明确归纳方向，总结出被研究素材的共性特征；③猜想共性因素与规律；④证明猜想。

案例6  “钉子板上的多边形”的教学

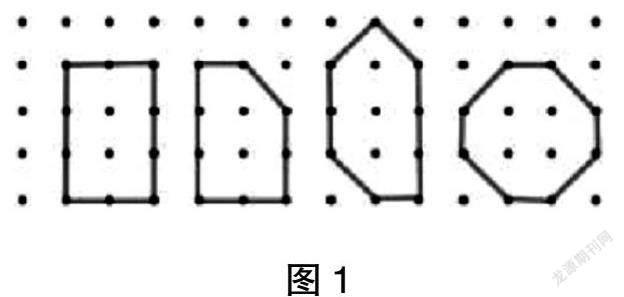
教师可引导学生先探究多边形中间有1颗钉子的情况，发现“面积都是多边形边上钉子数量的一半”的结论。如果离开这个前提，那么这个规律就不复存在。在此基础上，再引导学生探索多边形中间有2颗钉子的情况。

如图1，数一数多边形的钉子数量，计算面积，并对数据进行综合分析。随着问题的逐个突破，再引导学生探索、猜想多边形内部存在3、4、5……颗钉子的多边形面积与围成该多边形所需钉子数量的关系，让学生通过画一画、算一算，验证自己的猜想。

学生的思维随着问题的逐渐深入而发散，最后一段猜想关系的内容已经上升到演绎推理的范畴，对学生的思维要求更高。该活动过程不仅凸显了数学的本质，还让学生亲历了归纳推理的全过程。

（三）增强反思意识，积累推理经验

弗赖登塔尔认为：反思是学生思维活动的动力与核心。于学生而言，每个知识的学习都是一种经历，只有将这一个个经历上升为自己的经验时，才彰显出学习的价值与意义［３］。反思就是从一次次经历中总结经验的过程。问题的解决并不代表思维活动就此终止，很多时候是深入认识的起点。从感性认识上升到理性认知过程，反思充当了桥梁的作用，而缺乏反思的学习是不完整的学习过程。

培养学生的反思意识，促进反思习惯的形成，不仅能丰富教学活动过程，还能让学生在反思中积累推理经验和获得相应的思想方法。但反思习惯的形成离不开教师长期的引导与渗透，只有不断地给学生提供反思机会，才能让学生沉淀出相应的经验与方法。

总之，归纳推理贯穿于整个小学阶段，教师应明确每个阶段学生所适用的归纳推理目标，让学生在循序渐进中获得良好的学习方法与技巧，形成可持续性发展的学习能力，为学生数学核心素养的形成奠定基础。

参考文献：

［１］ 吴维维，邵光华. 逻辑推理核心素养在小学数学课堂如何落地［Ｊ］. 课程·教材·教法，２０１９，３９（０３）：８８－９５.

［２］ 史宁中. 试论数学推理过程的逻辑性——兼论什么是有逻辑的推理［Ｊ］. 数学教育学报，２０１６，２５（０４）：１－１６＋４６.

［３］ 弗赖登塔尔. 作为教育任务的数学［Ｍ］. 陈昌平等译. 上海：上海教育出版社，１９９５.

作者简介：马秋琦（1996—），本科学历，中小学二级教师，从事小学数学教学工作。