有趣的一笔画

小朋友，一笔画指的是在画一个图形时，笔尖从图上的某个点出发（笔尖不离纸），沿着图中的线开始画，每一条线只画一次，画出这个图形。

早在18 世纪，数学家欧拉就找到了画一笔画的规律。欧拉认为，能一笔画出的图形必须是连通图（连通图是指一个图形的各部分总是有线相连），但不是所有的连通图都可以一笔画完。能否一笔画完是由图形上奇点、偶点的数量来决定的。

什么是奇点和偶点呢？

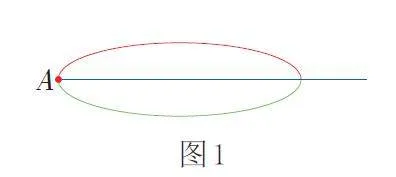
与奇数条线连接的点叫作奇点。例如： 如图1 所示，从A 点出发，可以引出3 条线，3 是奇数，所以A 点是奇点。

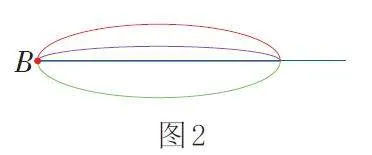
与偶数条线连接的点叫作偶点。例如： 如图2 所示，从B 点出发，可以引出4 条线，4 是偶数，所以B点是偶点。

画一笔画的规律是：

1.凡是由偶点组成的连通图，一定可以一笔画成。画图时可以把任一偶点作为起点，最后一定能以这个点为终点画完此图。

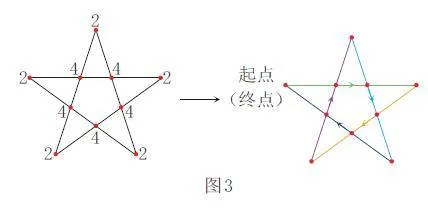
例如：图3 中的五角星形，图中所有的点都是偶点，从任意一个偶点出发，都可以一笔画出五角星形。

2.凡是只有两个奇点的连通图（其余的点都为偶点），一定可以一笔画成。画图时必须把一个奇点作为起点，另一个奇点作为终点。

例如：图4 中的图形，图中有两个奇点、两个偶点，把左边的奇点作为起点，右边的奇点作为终点，可以一笔画出这个图形。

3.其他情况的图都不能一笔画出。

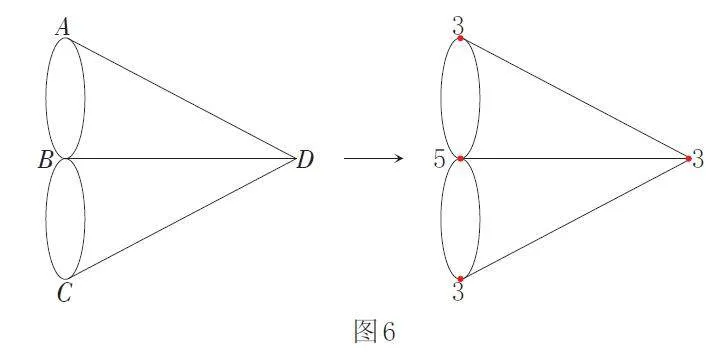
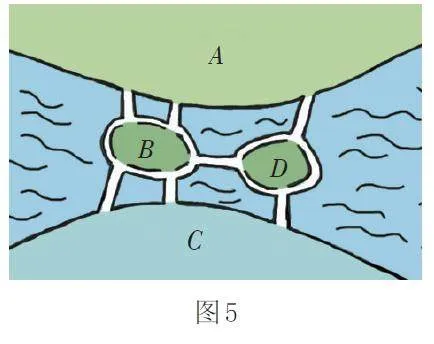
例如：著名的七桥问题。在一个公园里，有一条河穿过，河上有两座小岛，有七座桥把两座岛与河岸连接起来（如图5）。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点？

把七桥问题转化成一笔画问题（如图6），我们可以看到，从A 点、B点、C 点、D 点引出的线的条数均为奇数条，当奇点超过2 个时，是不能一笔画成的，所以，找不到能一次走过每座桥而不重复的路线。

小朋友，赶紧试试这一笔画的小妙招吧！