入水角度对球体高速入水空泡特性影响研究
李利剑,张敏弟,王占莹,黄彪,刘思华,谭镇坤
(1.北京理工大学 机械与车辆学院,北京 100081;2.北京宇航系统工程研究所,北京 100076)
入水过程是指物体以一定初速度从空气穿过气水交界面进入水中的过程,也就是从物体触及水面直至进入水中且在水中稳定运动到水底[1-2]的整个过程。入水现象在自然学科、工业生产、仿生技术、航空航天[3]以及海战装备和海洋开发[4-5]等领域都有广泛的应用。随着人们对能源需求的日益增长,世界各国开始重视起海洋资源开发,在海洋开发过程中,都会涉及到入水问题。如船锚入水、海洋钻井采油平台、水下生产设备吊装入水等[6]。由于入水运动涉及固、液、气的三相耦合作用,是一个具有强瞬态和非定常特性的过程,同时还伴随着湍动、相变、可压缩、介质突变等复杂流动现象[7-10],极易造成物体运动过程中结构的破坏及内部组件损坏、失灵和运动失稳等故障。因此,研究物体入水过程中空泡演化及其流体动力特性对于优化水下生产设备的设计,提升海洋开发机械的入水品质,以及推动水动力学基础理论的发展都具有非常重要的意义。
早在19 世纪末期,Worthington 等[11-12]采用单闪照相机对物体入水过程进行了初次探索,获取了第一张入水运动的照片,首次系统地描述了入水过程中产生的喷溅、生成的空泡和空泡闭合等流动现象,定性分析了入水空泡的演化过程及影响空泡生成的部分因素。之后40 年对入水现象的试验研究都是基于Worthington 的研究方法进行模仿或者改进,而且他对入水现象的部分定义一直沿用至今。对于入水问题的研究主要集中在入水空泡发展过程研究、入水冲击与水动力研究以及射弹入水稳定性研究3 个方面。
对于物体入水空泡演化方面,May 等[13-15]展开了大量具有军事应用背景的入水机理试验研究,开展了球体几何外形、傅汝德数等因素对球体高速入水过程中空泡形态及球体所受阻力的影响研究。Truscott 等[16]开展了密度和表面润湿性对球体垂直入水时空泡的发展规律及流体动力特性影响的研究,并且基于图像处理技术获取了入水过程中球体的位移、速度等运动参数,分析了流体动力特性。张孝石等[17]通过水洞试验对通气空泡的溃灭特性进行了研究,结果表明,在航行体停止通气后,空泡经历了空泡凹陷、空泡断裂、空泡脱落和溃灭4 个阶段。空泡脱落时,在脱落空泡区域形成射流,航行体表面承受冲击波压力,随后冲击波压力迅速衰减。李达钦等[18-19]采用试验观测和数值计算相结合的方法,对不同密度比的疏水性球体垂直入水空泡形态及水下流体动力特性进行了研究,此外还分析了旋转球体入水过程中空泡的演化历程,认识到角速度对空泡的喷溅、形态有显著影响,但对空泡夹断深度影响不大。
对于物体入水冲击载荷与弹道稳定性方面,El Malki Alaou 等[20]同样结合试验观测和数值模拟对不同锥角回转体入水过程开展了研究,重点关注了不同头部锥角回转体入水时的冲击载荷。黄鸿鑫等[21]通过数值模拟方法,从空泡形态、速度衰减以及俯仰角变化探讨了射弹头部形状和质心位置对高速入水稳定性的影响。胡青青[22]探讨了弹体高速时头型和长细比对入水弹道稳定性的影响,并分析了其对入水过程的影响。Moxnes 等[23]通过试验分析和数值模拟计算总结了不同类型的射弹在水中发生跳弹的规律。陈诚等[24]开展了入水角为20°时带圆盘空化器超空泡航行器倾斜入水试验,针对入水冲击载荷进行了研究。侯宇等[25]通过试验研究了射弹小角度高速入水过程中的弹道特性,分析了弹体不同侧滑角入水冲击过程的弹道轨迹、喷溅演变和水下压力波传播特征,发现在高速入水过程中,增大射弹侧滑角,会降低射弹入水弹道的稳定性。周可等[26]采用数值模拟的方法对跨介质航行器高速斜入水跳弹现象进行了研究,结果表明,航行器高速入水时,头尾两侧受力不均,形成了向上的偏力矩,改变了航行器的俯仰角,航行体入水角度越小,越容易发生跳弹现象。2021 年,田北晨等[27]针对入水参数对跨介质飞行器静水情况下近水面处滑跳运动过程进行了数值模拟,结果表明,跨介质飞行器在近水面处滑跳运动可分为稳定滑跳阶段及水面滑行阶段。稳定滑跳阶段飞行器的运动轨迹呈类正弦规律波动,逐次入水砰击瞬间,飞行器均会受到较大的砰击载荷。跨介质飞行器近水面滑跳运动过程中,入水速度越大,砰击载荷越大,稳定滑跳次数越多,稳定滑跳距离越远。
入水过程对于反潜武器能否成功入水并准确打击目标起着至关重要的作用。目前对于射弹高速入水稳定性的研究主要是从入水冲击载荷和弹体头型等方面进行,针对入水角度对弹道稳定性的影响也开展了一定的研究。但是,在研究入水角度对弹道稳定性影响的过程中,从入水空泡演化的角度进行的研究还不充分,而入水空泡的演化对反潜武器入水瞬间的流体动力特性和水下弹道的稳定性具有重大的影响。因此,本文针对球体,结合试验观测与数值模拟讨论了高速运动的球体以不同入水角度入水时空泡的演化过程,分析明确入水角度对空泡流动特性的影响。
1 试验系统及数值计算方法
1.1 试验系统
基于高速摄像机搭建的球体入水观测平台如图1所示,平台由发射系统、水箱、图像采集和处理系统组成。其中,发射系统主要由角度调节装置和发射装置组成。角度调节装置由支撑板、支架上的定位孔和支撑轴组成,试验中通过将支撑板固定到不同的定位孔实现球体以不同角度入水。发射装置由空气压缩机、电磁阀、安全阀和发射管组成,试验中打开安全阀,通过压气机提供高压气体膨胀做功提供驱动力,在电磁阀开启瞬间,球体在高压气体的驱动下,经由发射管中加速发射。通过调节压气机内高压气体压力和流量控制球体的速度。高压气缸内气体压力与速度的关系[28]为:
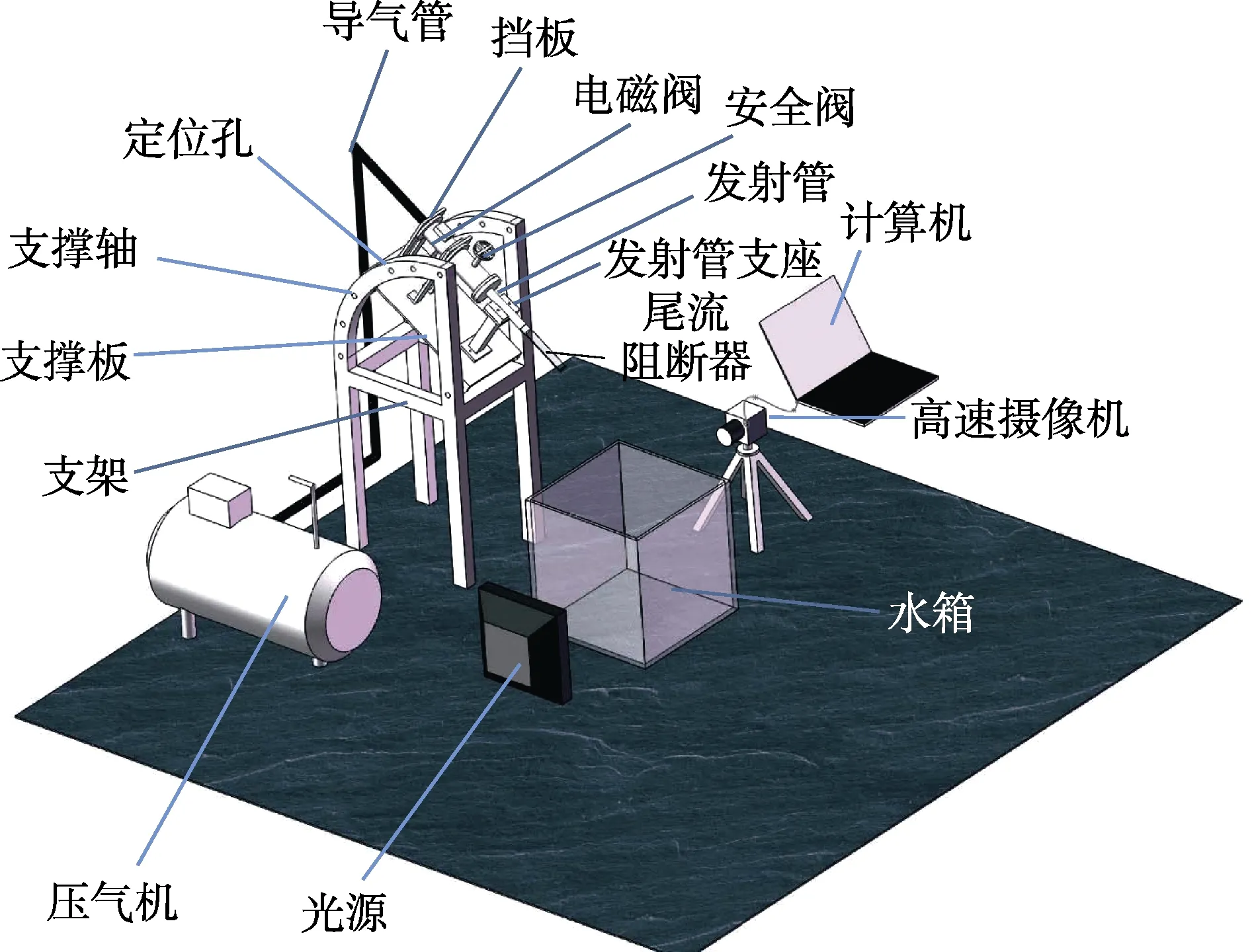
图1 球体入水观测平台 Fig.1 Water entry observation platform of sphere
式中:P1为压气机内压力;V为压气机容积;k为气体绝热指数;L为发射管长度;A为发射管面积;P为大气压力;Mdan为球体质量;φ为次要功系数,用于能量损耗的修正,一般为1.02~1.1;v为球体运动速度。
试验水箱尺寸为0.6 m×0.6 m×0.6 m,四周及底面均为10 mm 厚的有机玻璃,在水箱底部垫有厚度为0.1 m 的缓冲层,防止球体高速入水时与水箱底部发生撞击而损伤水箱。试验球体直径为D=5 mm,密度为7 850 kg/m3。图像采集和处理系统由高速摄像机、光源和计算机组成。试验中,将高速摄像机放置在试验水箱正前方,采集频率设为4 000 fps。采用多通道同步触发器同步触发电磁阀和高速摄像机,实现球体入水过程的实时记录和实时显示。光源布置为阴影法布局,记录入水空泡演变过程形成阴影,进而分析提取空泡轮廓和流场流动结构。
1.2 数值计算方法
在入水过程中,存在气、液两相界面的运动和变形。本文假定气、液两相为均相流动,采用VOF 方法通过容积跟踪法对相界面进行追踪。控制方程为:
式中:ρm为混合介质的密度;μm为混合动力黏性系数;p为静压强;g为重力加速度;μt为湍流黏性系数;ui、uj分别为i、j方向的速度分量。对于ρm和μm,其表达式为:
式中:α表示蒸汽体积率,表征水、汽两相之间的相变;ρ为介质的密度;下标v、g、l 分别表示蒸汽、空气和水。
湍流模型选择由Launder 和Spalding 提出的k-ε标准湍流模型,它把涡黏系数和湍动能k及湍动能耗散率ε联系在一起,控制方程为:
式中:Pt为湍动能生成项;σk、σε、Cε1、Cε2为常数,根据经验[29],取值分别为1.0、1.3、1.44、1.92。
球体在高速入水时会发生空化现象,基于质量传输的空化模型,其组分传输方程为:
式中:为单位体积质量传递速率;+为单位体积液体质量传递速率;为单位体积蒸汽质量传递速率。
Zwart-Gerber-Βelamri 空化模型结合泡间两相流动理论,重点考虑空穴生长和溃灭时气泡体积变化的影响,适用于空化的非定常过程。在该模型中,单位体积内的相间传输速率为:
式中:αnuc为汽核体积分数;RΒ为汽泡半径;pv为汽化压强;Fvap和Fcond分别为蒸发和凝结经验系数。
本文采用的计算域以及边界条件设置如图2 所示。设置球体直径D=5 mm,与试验所用球体直径一致,计算域长、宽、高分别为143.4D、120D、60D,其中空气域高43.4D,水域高100D,球体底部距离自由液面3D。球体周围及自由液面处网格进行加密,分离求解算法采用SIMPL 算法,压力项采用PRESTO格式,空间与时间离散采用一阶迎风格式。
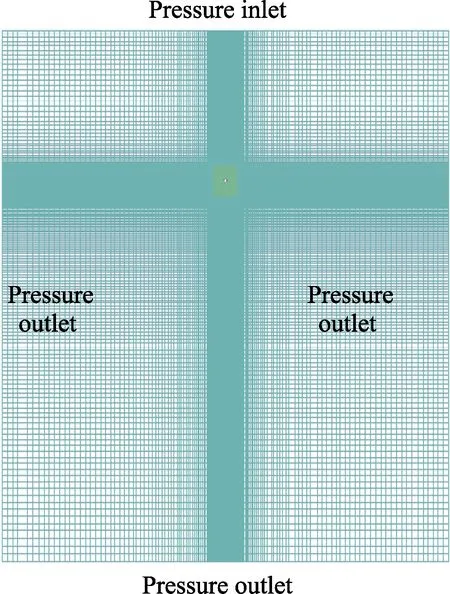
图2 计算域网格及边界条件设置 Fig.2 Settings of computational domain mesh and boundary condition
为了验证所采用的数值计算模型,对球体以30 m/s 垂直入水过程进行了数值模拟,并与试验结果进行对比。数值模拟与试验所得球体入水深度随时间变化曲线如图3 所示,数值模拟得到的球体位置与试验测得的位置误差在5%以内。试验观测和数值模拟得到的空泡闭合轮廓如图4 所示。由图4 可见。数值模拟提取的空泡轮廓与试验采集得到结果基本完全吻合。对比图3 和图4 结果可知,本文构建数值模拟方法可靠可信,能够用于后续研究。

图3 入水深度随时间变化曲线 Fig.3 Curve of water entry depth over time

图4 试验与数值模拟空泡闭合形态对比 Fig.4 Experimental and numerical simulation of cavity closure patterns
2 结果与分析
2.1 球体垂直入水空泡演化研究
2.1.1 演化过程
基于试验观测,本文根据球体入水过程中入水空泡的形态特征将入水过程分为入水冲击、空泡形成、空泡闭合和空泡溃灭 4 个阶段。速度v=30 m/s时球体入水空泡演化过程如图5 所示。在t=0 ms 时刻,球体撞击水面,与水体产生动量交换,使得水体排向周围,在与球体的接触面处发生流动分离,形成喷溅。随着球体入水深度的增加,喷溅水膜的厚度也逐渐增大,进一步发展成对称的水冠。同时,球体在运动过程中挤压周围水体,在水中形成空泡,空气流入空泡内部,空泡逐渐被拉长。在空泡闭合阶段,随着动能逐渐耗尽,液膜在重力、压差阻力以及表面张力的作用下逐渐收缩闭合,从而切断了外界空气与空泡的联系。当球体继续向下运动时,空泡受到球体的作用,脱离自由液面,进一步发生面闭合,并产生较强的回射流。空泡闭合时产生的回射流会冲击空泡壁面,导致壁面不稳定,同时因空泡尾部动能耗尽而不断收缩,导致空泡夹断溃灭。然而,空泡溃灭夹断时也会产生回射流,进一步引起空泡的溃灭。
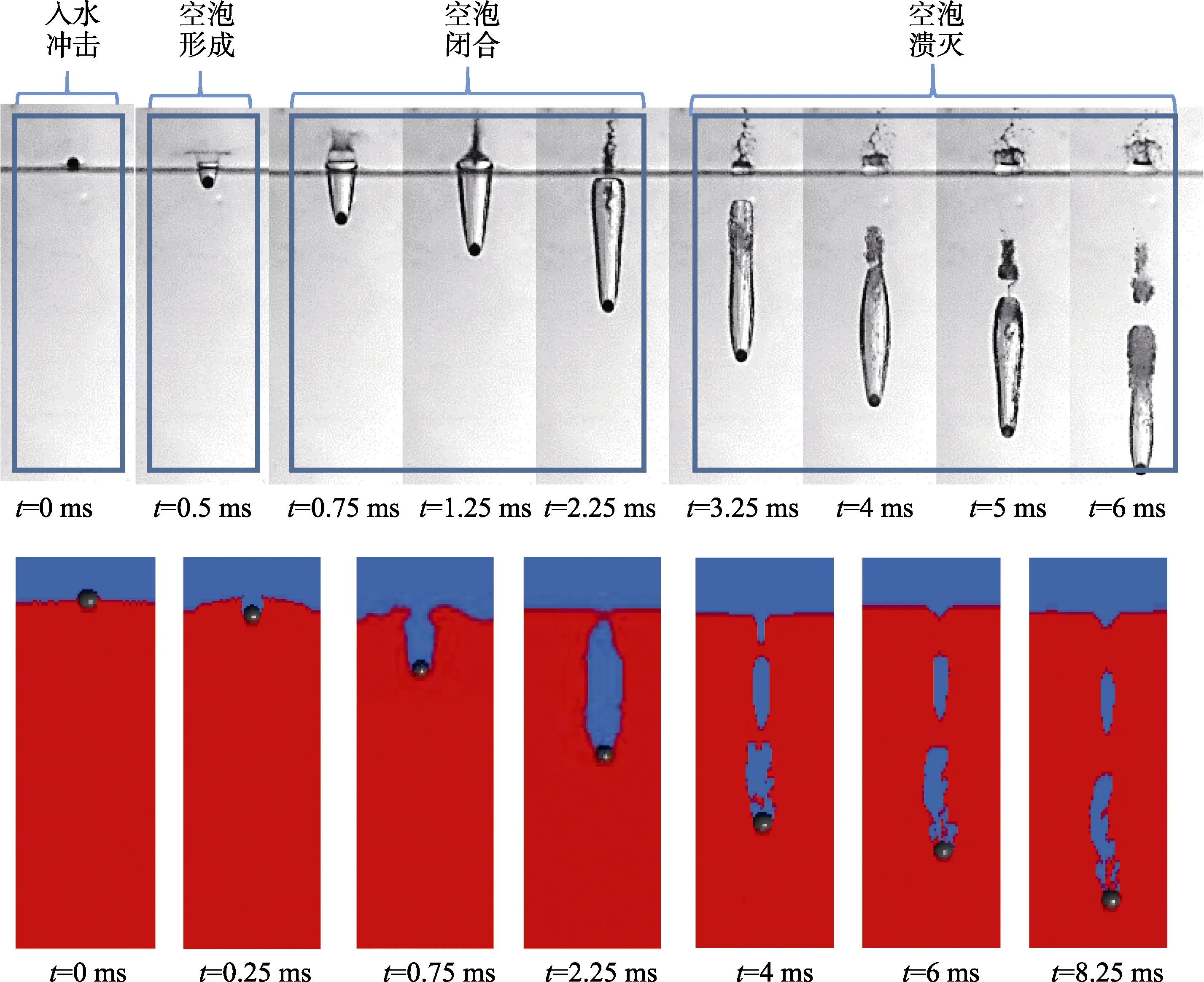
图5 球体入水空泡演化过程 Fig.5 Evolution process of sphere’s water entry cavity
2.1.2 演化特性分析
在入水冲击阶段,球体撞击自由液面,与周围流体接触,并发生动量交换,周围流体获得动量,形成喷溅。入水冲击阶段和空泡形成阶段的流场图像和压力分布云图如图6 和图7 所示,球体入水时喷溅的受力分析如图8 所示。由图6 压力场可知,球体与水面接触部分压力明显高于周围流场压力,而在球体未接触水面部分形成了对称的低压区域。这是由于高速运动的球体扰动周围空气,使周围空气流速增大,压力降低。根据压力分布云图可知,水体在接触球体位置压力最大,高达0.638 MPa,离球体越远,压力越小。随着入水深度的增大,水体与球体发生流动分离,形成水冠,由于球体周围压力较低,空气流入空泡内部,球体开始携带空泡向下运动,且入水空泡始终与大气相连。由图7 压力与矢量分布可知,空泡内部出现明显的低压区,气体高速流入空泡内部,同时球体头部的高压区域也明显减小,此时球体头部的压力为0.357 MPa,比入水冲击时减小44.0%。图8 中,Uwater为液膜顶端运动速度,对应加速度为as,液膜所承受的主要受力包括自身重力Fgs、由于气流高速运动所产生的压差力FΔp、流动阻力Fd以及阻碍液膜运动的表面张力Fσ。取一液膜微元,质量记为ms,可建立受力平衡方程如下:

图6 入水冲击成阶段试验图像与压力分布云图 Fig.6 Experimental image and pressure distribution pattern during water entry impact
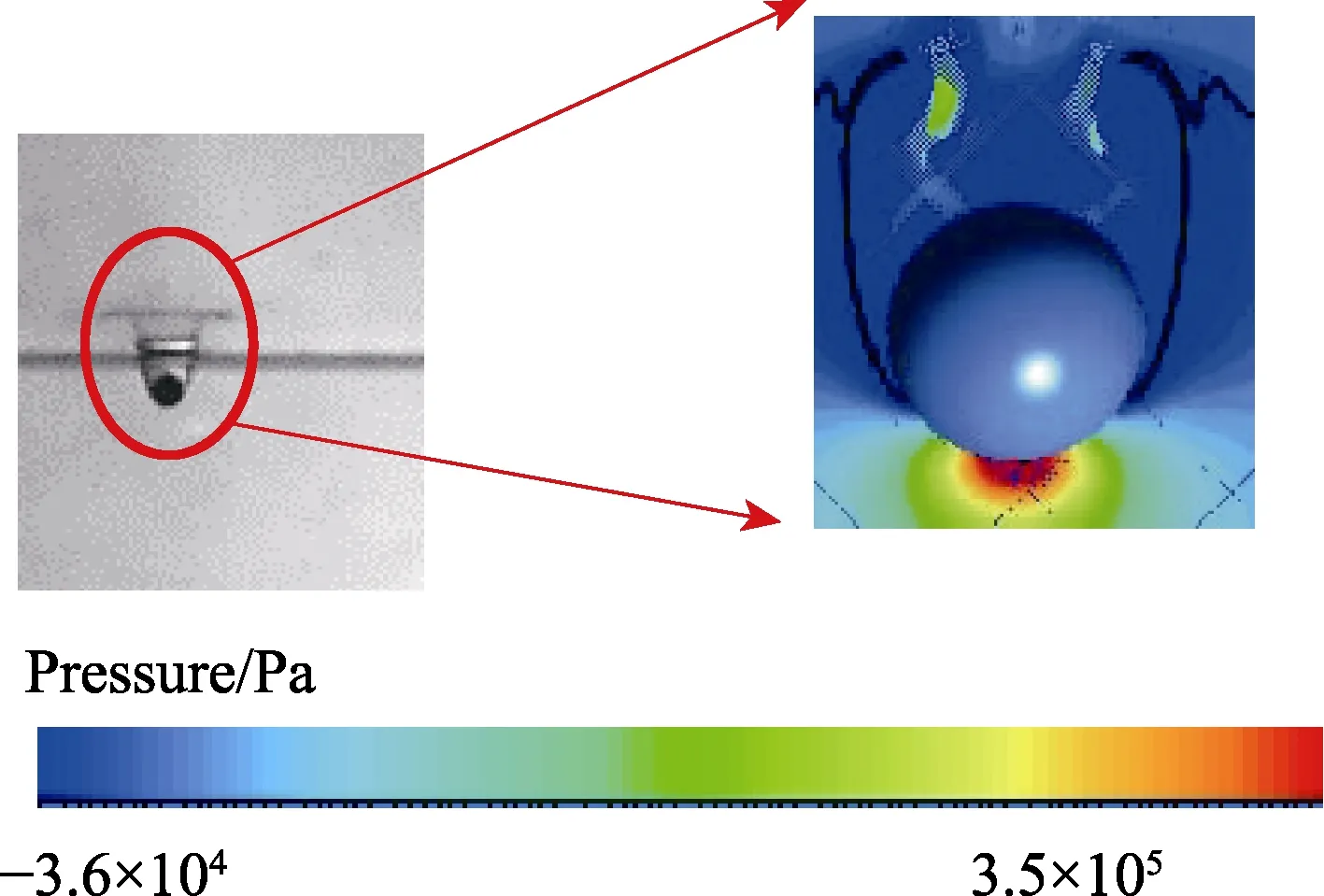
图7 空泡形成阶试验图像与压力分布云图 Fig.7 Experimental image and pressure distribution pattern during cavity formation
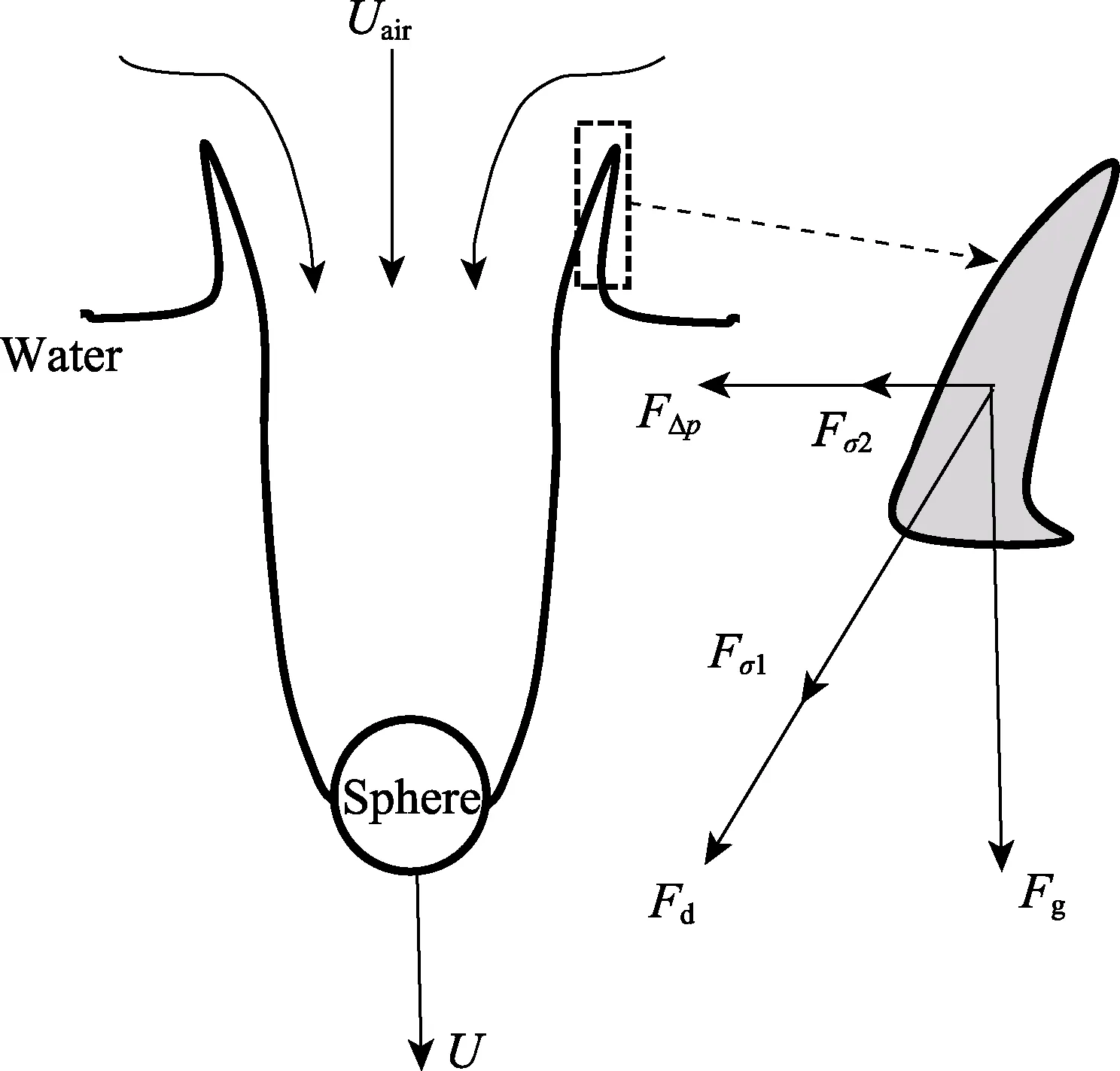
图8 喷溅受力分析 Fig.8 Analysis of splash force
式中:流动阻力Fd与速度平方成正比,压差力FΔp的定义为:
式中:ΔAs为液膜微元的截面积;ps为喷溅内压强;p∞为环境压强,p∞=101 325 Pa;ρg为气体密度;Uair为当地气流速度;dVc入水空泡体积增量成;Ds为空泡直径。由以上分析可知,喷溅的形状与运动与空气流速Uair有关,空气流速Uair越大,压差力FΔp越大,向内收缩越快。
由图9 可知,在空泡闭合过程中,空泡内部压力较低,空泡周围喷溅区域的外侧压力较高,在内外压差的作用下,空泡不断向中间收缩,此时向空泡内部运动的气体的最大速度也降低到2 m/s,远远小于空 泡形成阶段的气体流速。进一步分析此时流场受力分布情况,并绘制了空泡形成阶段出现喷溅时的受力示意图(图10)。图10 中,Uwater为液膜顶端运动速度,对应的加速度为ac,液膜所承受的主要受力包括重力Fgc、气流高速运动所产生的压差力FΔp、流动阻力Fd以及阻碍液膜运动的表面张力Fσ。取一液膜微元,质量记为mc,可建立如下受力平衡方程:
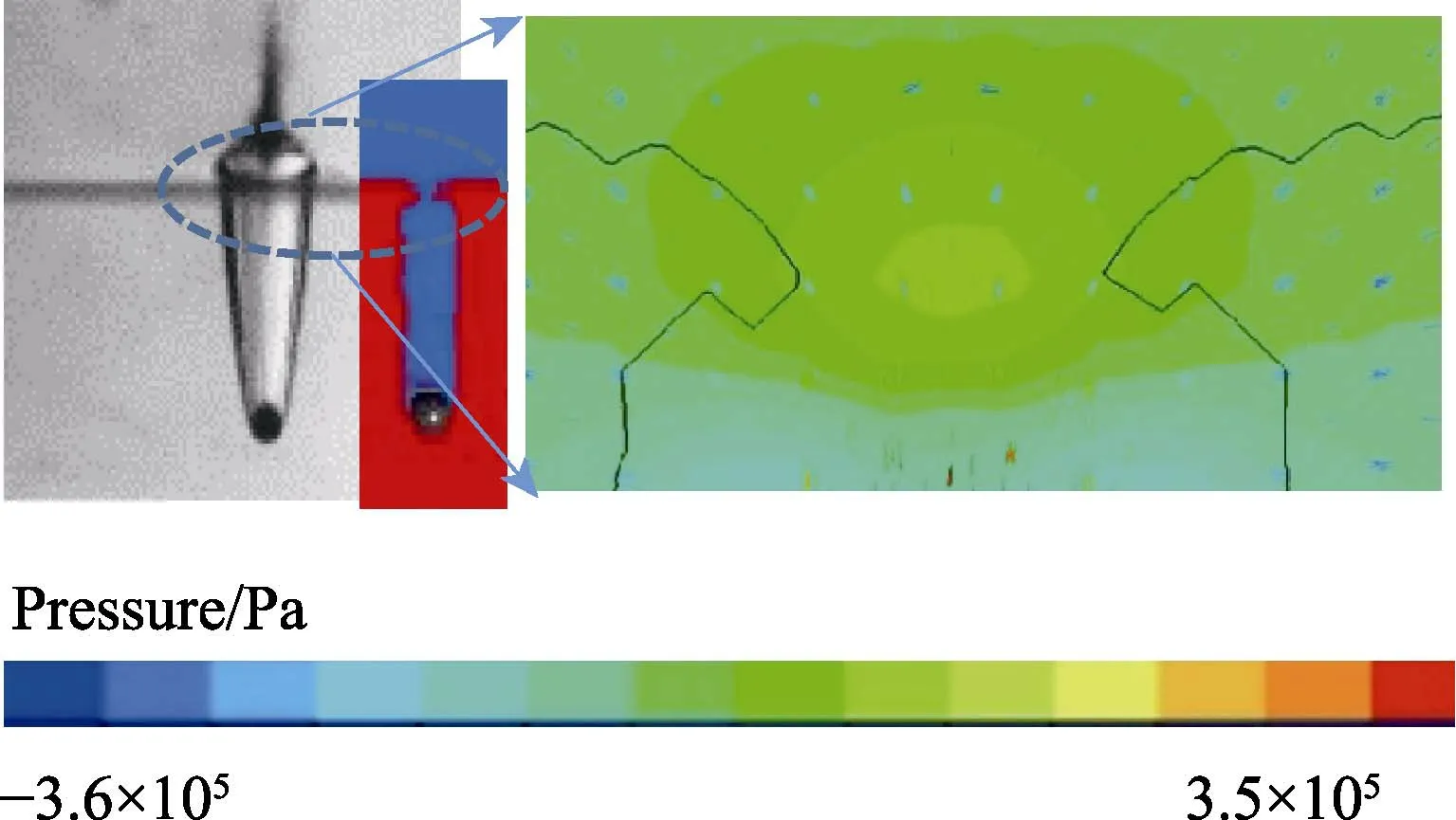
图9 空泡闭合过程试验图像与压力、速度矢量分布 Fig.9 Experimental image and distribution of pressure and velocity vectors during cavity closure
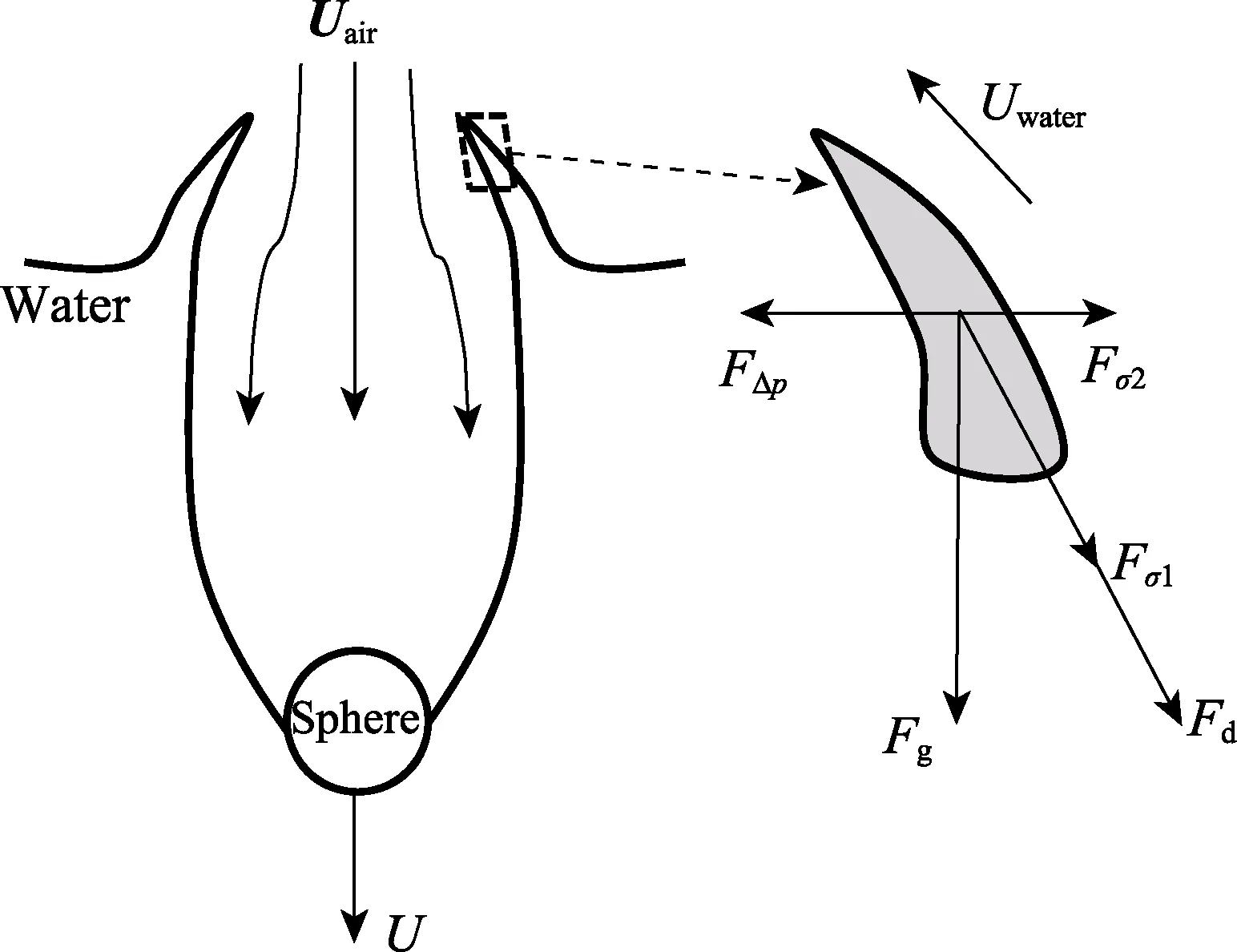
图10 空泡闭合阶段受力分析 Fig.10 Force analysis during cavity closure
式(14)中,压差力FΔp的计算方法与空泡形成阶段相同。由以上分析可知,空气的流速在空泡闭合阶段起着非常重要的作用,流入空泡内部空气的流速越大,压差越大,空泡闭合越快。此外,空泡闭合还受到液膜速度的影响,液膜速度越快,受到的流动阻力Fd越大。液膜速度、空气流速都与球体的运动有关,因此球体的运动参数(如角度、速度)对空泡的闭合起着至关重要的作用。
空泡溃灭阶段的试验图像与压力、速度分布云图如图11 所示。随着球体继续向下运动,空泡尾部水体向四周扩张的速度小于0.5 m/s,空泡尾部壁面动能耗尽,发生溃灭。由图11 可见,球体头部压力仍明显高于其他区域的压力,但由于球体运动速度减小,球体头部的压力也发生了减小,此时球体头部压力为0.18 MPa,减小到入水冲击时压力的36%,空泡形成阶段压力的71.8%。另外,在空泡的收缩处压力较高,而收缩段下方压力明显低于其他区域。进一步对收缩段流场进行受力分析,收缩段空泡形态特征如图12 所示。在空泡脱离自由液面后,随球体向下运动的空泡的不同区域会同时存在收缩和膨胀2 种状态。造成这种现象的原因主要是,空泡闭合后不再有空气进入空泡内部,随着球体向下运动,空泡在拉扯力的作用下会趋于细长,同时静压强随着入水深度逐渐增大,空泡会在某一动能小于压能的位置处迅速收缩,并与静压强平衡,此时收缩处空泡直径变小,气体只有流入其他空泡区域,且导致体积增加。

图11 空泡溃灭时的试验图像和局部压力、速度分布云图 Fig.11 Experimental image and local pressure and velocity distribution pattern during cavity collapse

图12 空泡收缩段形态特征 Fig.12 Morphological characteristics of cavity contraction segment
2.2 入水角度对入水空泡演化的影响
速度为30 m/s 的球体以不同角度入水的空泡演化过程如图13 所示。图13a 中,t=0 ms 时,球体先撞击液面形成喷溅。t=0.5 ms 时,喷溅继续扩展,形成了对称的水冠,水冠在重力、表面张力以及内外压差的作用下开始收缩,直至喷溅发生闭合,阻断了外部空气的进入(t=0.75~1.25 ms)。随着球体继续向下运动,入水空泡也随着球体向下运动,已经切断了和空气连接的空泡受到向下拉扯的作用力,当作用力大于空泡所受到的表面张力时,空泡就会从自由液面脱落,发生面闭合,并产生比较强的回射流(t=2.25 ms)。回射流的冲击会导致空泡壁面不稳定,同时在静水压的作用下,空泡尾部开始收缩溃灭,此时空泡形状呈梭形(t=2.25~4 ms)。在空泡溃灭夹断时,也会产生回射流,从而进一步地引起入水空泡的溃灭(t=5~ 6 ms)。球体在斜射入水时,空泡演变过程与垂直入水相似,均存在入水冲击、空泡形成、空泡闭合和空泡溃灭几个阶段,且都在空泡闭合时发生面闭合。但由于斜射入水时球体水平方向分速度的存在,导致其迎流面的喷溅较高、背流面的喷溅较低,进而影响了水冠的形态(如图13 b、c 所示)。其次,在入水空泡发生面闭合时,与垂直入水也有所区别,入水角度为60°时,空泡在t=3.25 ms 发生了面闭合,闭合时产生了微弱回射流。球体入水角度为30°时,入水空泡在t=9.5 ms 时发生了面闭合,此时空泡闭合没有产生回射流。随着入水角度的减小,空泡闭合时间逐渐增加,且产生的回射流在逐渐减弱。在入水角度为30°时,空泡面闭合不再产生回射流。入水角度为60°和30°球体第一次溃灭夹断的时间分别为t=7.5 ms、t=36.5 ms,溃灭时间随着入水角度的减小而逐渐延迟。在空泡第一次溃灭时,都是以小尺度气泡团的形式溃灭。球体入水角度为60°的入水空泡与垂直入水时的入水空泡一样,第一次溃灭都产生了回射流,但以30°入水时,入水空泡第一次溃灭并未产生回射流。此时,入水角度为30°的入水空泡也与之前不同,空泡发生了抖动,不再呈现出梭形(图 13c 中t=36.5 ms)。入水角度为30°的入水空泡在第二次溃灭时与第一次不同,第二次溃灭不再以小尺度气泡团的方式溃灭,而是断裂成多个尺度更大的气腔从空泡上脱离。

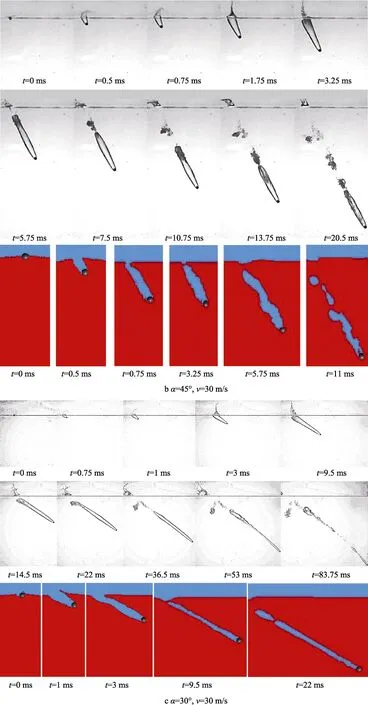
图13 球体以不同入水角度入水空泡演化过程 Fig.13 Evolution process of sphere’s water entry cavity at different water entry angles
由于球体的运动参数对空泡的闭合起着至关重要的作用,本文开展了球体以不同角度入水过程中空泡演化过程研究。球体入水位移、速度和加速度的时间变化曲线如图14—16 所示。这些曲线是依据对多组连续试验图像进行图像处理后,确定球体位置,进而结合记录频率,提取球体运动速度和加速度绘制而成的。对比图14 中各条曲线可知,球体斜射入水时都发生了不同程度的偏离,并且偏离程度随着入水角度增大而减小,入水角度为30°时最大,入水角度90°时,几乎没有发生偏离。图15 中球体的速度总体上呈现减小的趋势,但在空泡闭合以及溃灭时出现了不同程度的增加,并且增加幅度随着入水角度的增大逐渐减小。在空泡溃灭阶段,球体以90°和60°入水产生的空泡在溃灭夹断时都产生了回射流,导致球体速度增加。空泡夹断溃灭时,球体90°入水形成空泡的回射流强度更大,速度增大也更多。入水角度为90°时球体速度相比溃灭前增加了2.08 m/s,入水角度为60°时,球体速度在夹断溃灭时相比溃灭前增加了1.403 m/s。
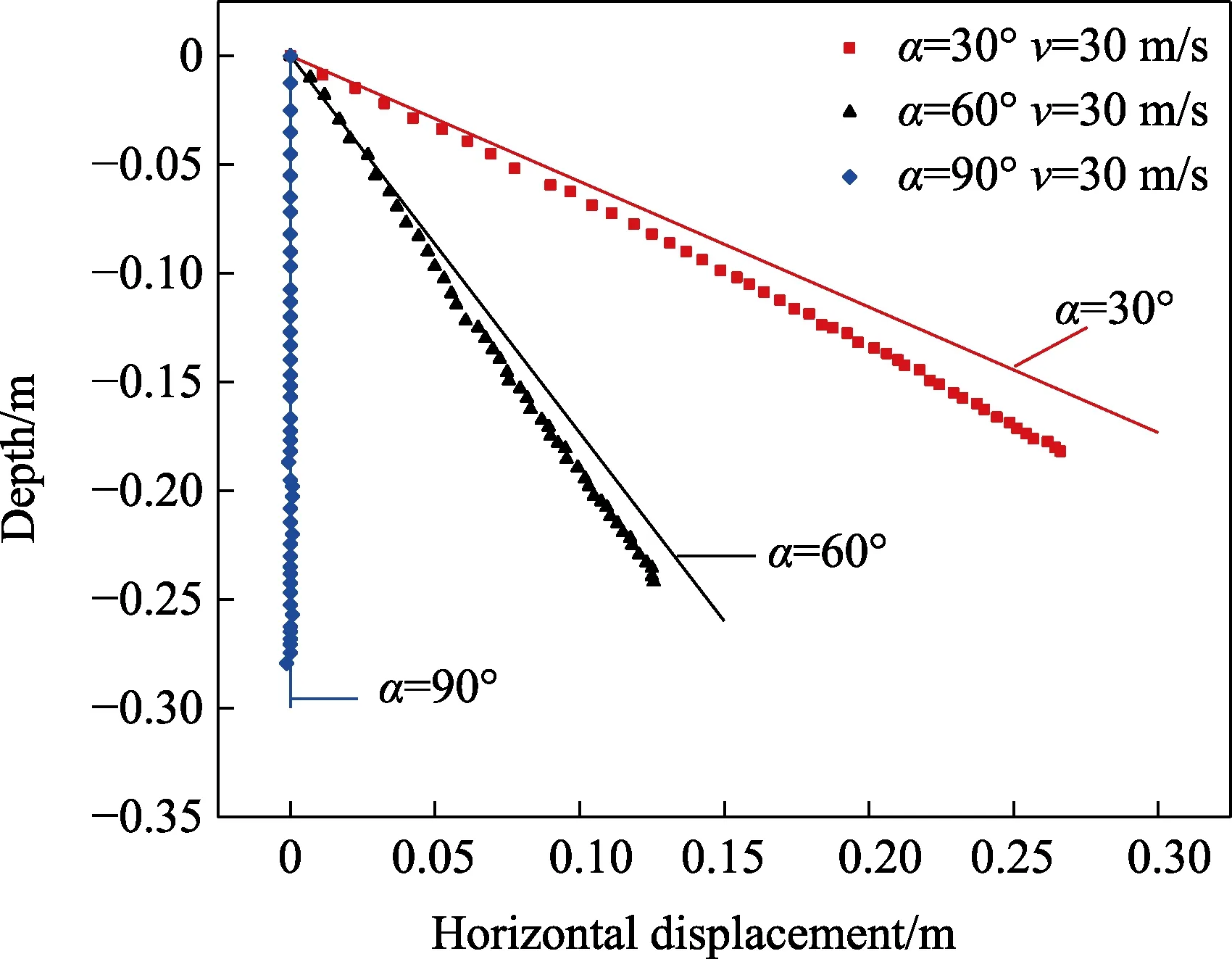
图14 球体以不同角度入水后坐标变化曲线 Fig.14 Coordinates of sphere after entering water at different angles

图15 球体以不同角度入水后速度随时间变化曲线 Fig.15 Velocity of sphere over time after entering water at different angles
对比图16 中各条曲线可知,所有工况下球体加速度的绝对值都在入水的瞬间达到最大,且随着角度的增大,加速度峰值也在增大。不同入水角度下球体 入水5 ms 内加速度的波动范围见表1。由表1 可知,随着入水角度的增大,加速度波动越来越剧烈。加速度最大绝对值(即球体入水冲击时刻加速度的绝对值)随角度的变化曲线如图17 所示。由图17 可知,30°时加速度是最大绝对值为7 039 m/s2,60°时加速度的最大绝对值为14 215 m/s2,90°时为15 166 m/s2。对比各值可知,加速度最大绝对值随入水角度的增大而增大,但其增长速度随角度的增大而减小。
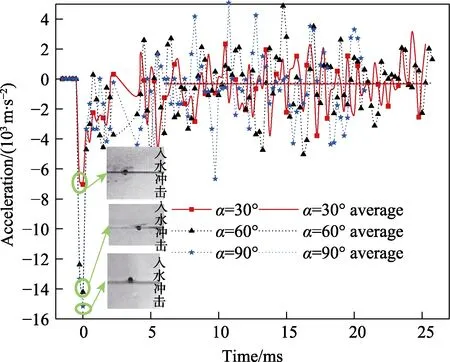
图16 球体以不同角度入水后加速度随时间变化曲线 Fig.16 Acceleration curve of sphere after entering water at different angles
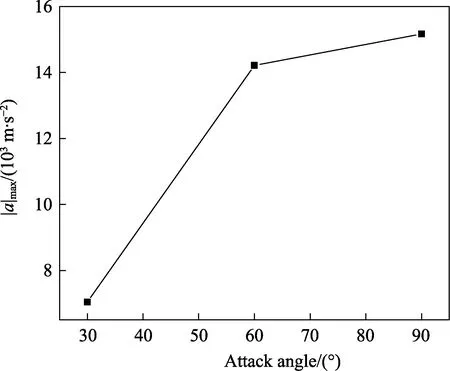
图17 球体加速度最大绝对值随入水角度变化曲线 Fig.17 Maximum absolute acceleration curve of sphere at different water entry angles

表1 不同入水角度球体入水5 ms 后的加速度波动的范围 Tab.1 Range of acceleration fluctuations of sphere 5 ms after entering water at different angles
2.2.1 入水角度对入水冲击和空泡形成的影响
球体以不同角度入水过程中,流场图像与压力分布云图如图18 所示。对比图18 中各图可知,随着入水角度的减小,球体头部沾湿处压力逐渐减小,沾湿区域的最大压力也随着入水角度的减小而减小。球体以90°入水时,头部压力为0.638 MPa;60°时球体头部压力减小到0.51 MPa,相比90°时减小了20.1%;球体30°入水时,球体头部压力仅为0.443 MPa,相比90°时减小30.6%。球体未沾湿处的低压区出现明显变化,球体以90°入水时,低压区在球体周围对称分布,两侧低压区面积相同。球体斜射入水时,低压区分布不再对称。球体入水角度为60°和30°时,球体迎流面低压区域的面积比背流面小,而迎流面区域的压力高于背流面压力。
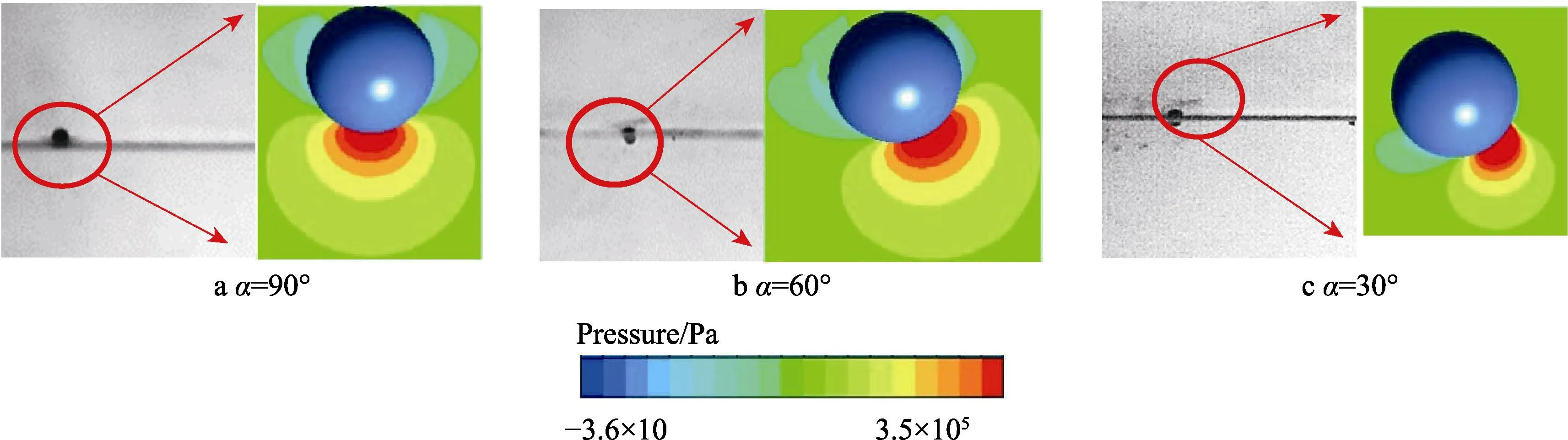
图18 入水冲击阶段试验图像和局部压力分布云图 Fig.18 Experimental image and local pressure distribution pattern during water entry impact
球体以不同角度入水时,空泡形成阶段的流场图像与压力分布云图如图19 所示。对比图19 中各幅图像可知,球体以不同角度入水时,在空泡形成阶段,球体头部沾湿区域都承受极高压力,随着入水角度的减小,球体头部沾湿处压力逐渐减小。球体以90°入水时,头部压力为0.357 MPa,相比入水冲击时减小44.0%;入水角度为 60°时,球体头部压力减小到0.349 MPa,相比入水冲击时减小31.6%;入水角度为30°的球体,头部压力仅为0.323 MPa,相比入水冲击时减小27.1%。空泡内部的压力低于水面上方的空气压力,气流高速流入空泡内部。球体以90°入水 时,空泡内的高速气流对称分布,随着入水角度的变化,高速气流的分布不再均匀。30°入水时,空泡内部高速气流仅分布在球体的左下侧。同时,随着入水角度的减小,流入空泡内气体的流速反而增加。球体以90°入水时,流入空泡内气体的最高流速为51 m/s;60°时气体的最高流速为73 m/s,相比90°入水增加43.1%;30°时气体的最高流速为132 m/s,相比90°入水增加158.8%。
2.2.2 入水角度对空泡闭合和溃灭的影响
球体以不同角度入水时,空泡闭合阶段的流场图像与压力分布云图如图20 所示。对比图20 中各图可 知,入水角度为90°和60°时,当空泡处于闭合过程中,液膜向中间收缩,流入空泡内的空气不断减少,在闭合处形成高压区域;球体以30°入水形成空泡后,在空泡闭合时,水体也向中间收缩,但由于流入空泡内气体的流速较低,未在闭合处形成高压区。
球体以不同角度入水时,溃灭阶段过程中的流场图像与压力分布云图如图21 所示。对比图21 中各图可知,球体以90°和60°入水时,入水空泡在尾部以小尺度气泡团的形式溃灭,同时在溃灭夹断处产生了回射流。当球体以30°入水时,空泡溃灭方式截然不同,没有出现小尺度的气泡团,而是断裂成较大的气腔,夹断处也没有回射流。由压力分布云图可知,球体入水角度为90°,当空泡溃灭时,收缩处的压力高于空泡内部其他区域压力,溃灭产生的回射流冲击到球体表面,气腔内部冲击区域的压力升高;球体入水角度为60°,入水空泡在溃灭时产生的回射流冲向空泡壁,导致气腔壁处压力升高;球体入水角度为30°,空泡溃灭时没有产生回射流,在空泡断裂处的压力与周围水体的压力基本一致。

图21 空泡溃灭阶段试验图像和局部压力分布云图 Fig.21 Experimental image and local pressure distribution pattern during cavity collapse
进一步对球体入水后的空泡进行分析,分别绘制了球体直径和最大截面面积随时间的变化曲线,如图22 和图23 所示。对比图22 中的各条曲线可知,球体以不同角度入水过程中,在空泡闭合时,泡径达到最大值,且空泡直径随着入水角度的增大反而减小。球体90°入水后,空泡闭合时的直径为2.2D;60°空泡闭合时的直径为3.03D,是90°空泡直径的1.38 倍;30°空泡闭合直径为5.32D,是90°空泡的2.42 倍。对比图23 中的各条曲线可知,球体入水角度为30°时,空泡分别在9、22、35 ms 出现了闭合、一次夹断溃灭和二次溃灭。在0~9 ms、9~22 ms、22~3 ms 时,空泡面积不断增加,但增加幅度各不相同。在9、22、35 ms 时,区域空泡面积达到极大值,35 ms 之后,残余空泡不断收缩溃灭。当球体入水角度为60°和90°时,空泡面积不断波动,与入水角度30°时空泡面积的变化趋势相似。在空泡闭合后,入水角度为60°和90°时,空泡面积远小于30°时的空泡面积,且随着入水角度的增大反而减小。球体在水下运动的受力分析如图24 所示。空泡闭合后,球体在水下运动时,受到的力主要有自身的重力mg、附加质量力Fa、浮力Fb、与运动速度平方成正比且与速度方向相反的流动阻力Fd以及空泡壁面的表面张力Fσ。受力平衡方程为:
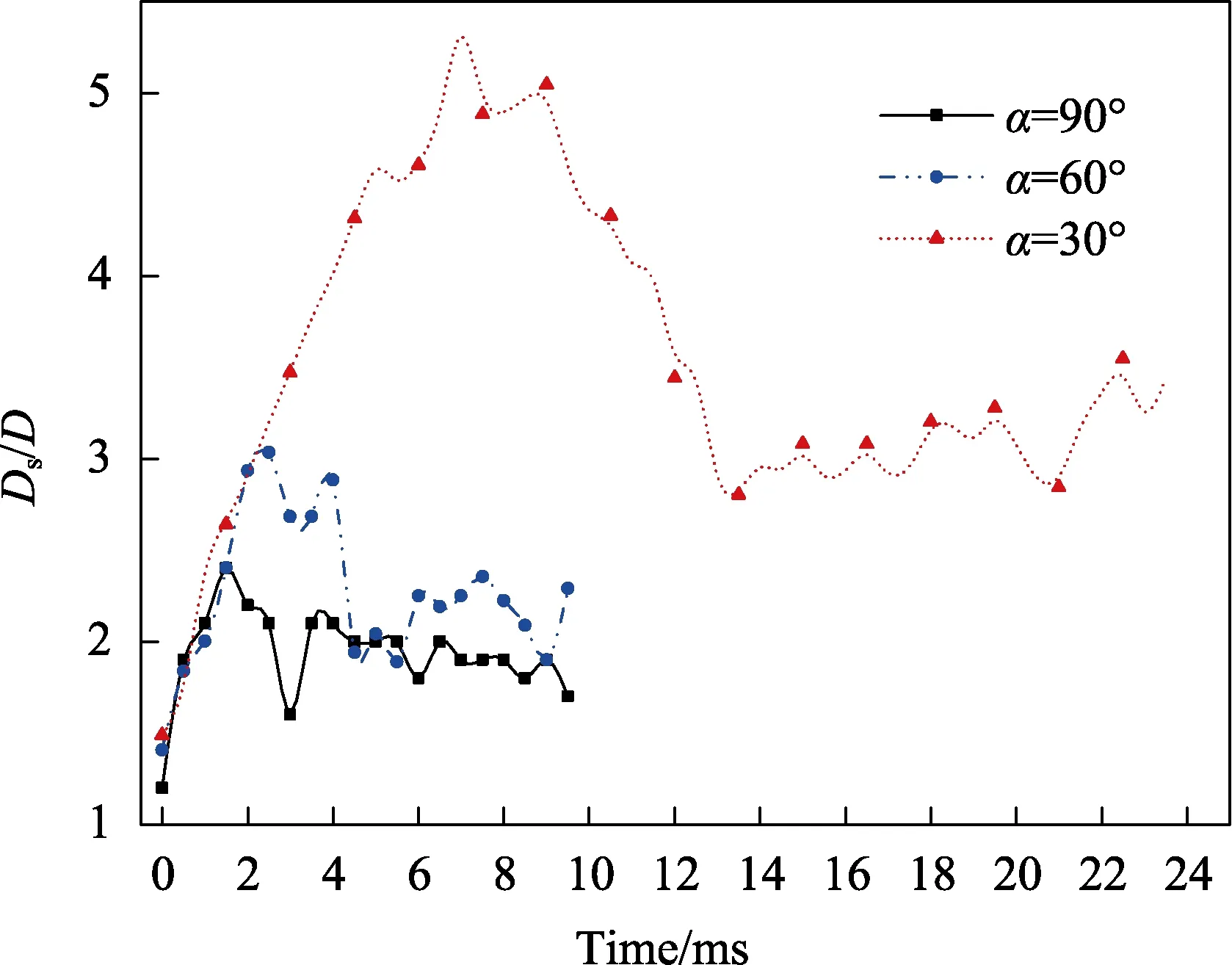
图22 空泡直径随时间变化曲线 Fig.22 Cavity diameter curve over time
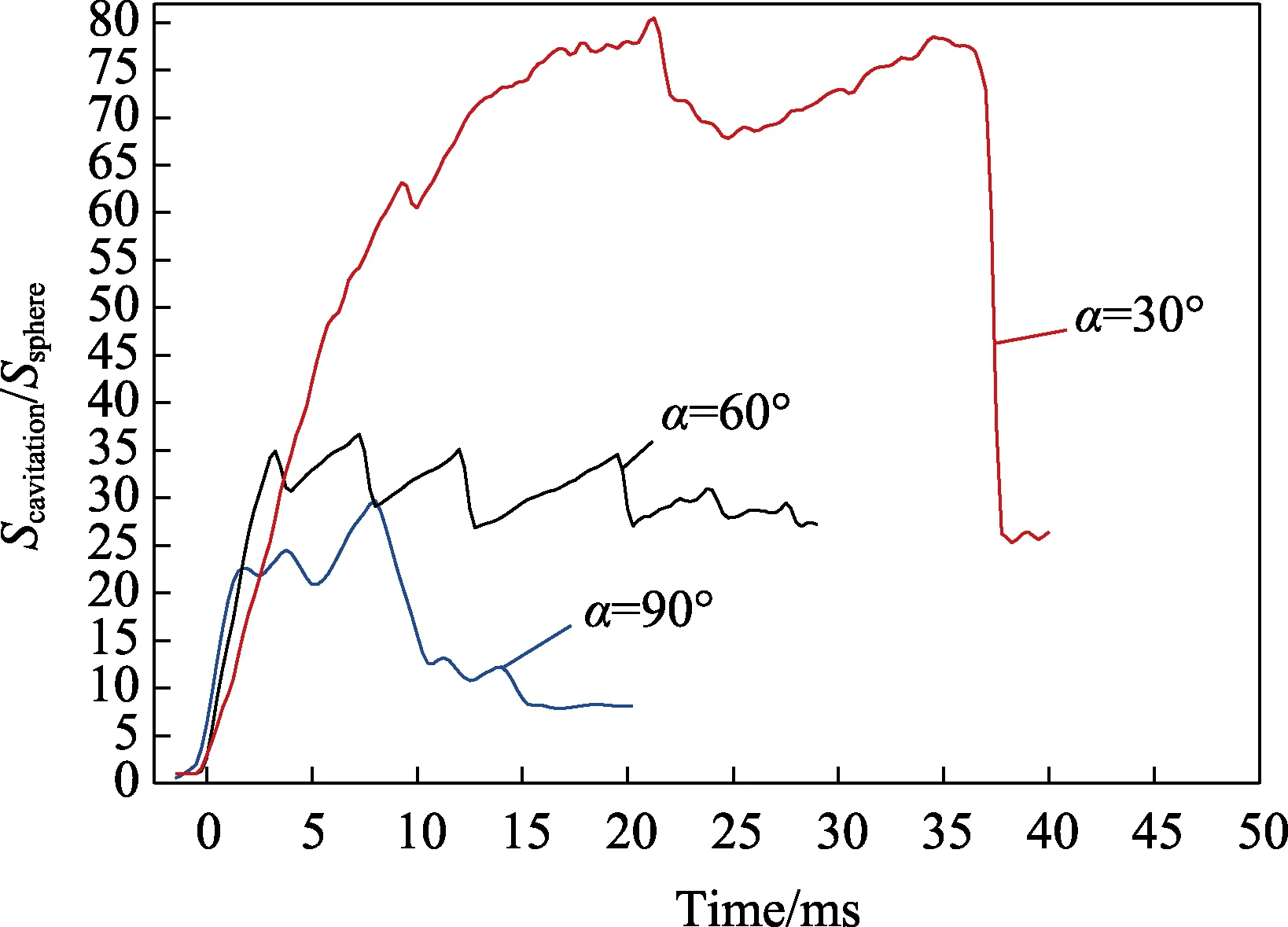
图23 空泡面积随时间变化曲线 Fig.23 Curve of cavity area over time

图24 球体水下运动受力分析 Fig.24 Force analysis of sphere in underwater motion
式中:m为球体质量;a为球体运动加速度。Fd、Fa、Fb、Fσ合力方向与运动方向相反,被称为总流体阻力F(t)。由于球体在水下运动时,表面张力Fσ对球体运动的影响非常微弱,可以忽略不计。根据以往学者的研究[30-31],附加质量力Fa可以定义为:
式中:Cm为附加质量系数;ρl为液体密度;V为球体体积;Vc为空泡体积;a为球体加速度。式(15)可以表示为:
因此,总流动阻力系数为:
由以上分析可知,球体在水下携带空泡运动的总流体阻力系数与空泡的体积有关,空泡体积越大,阻力系数越大。又由于空泡的体积与空泡的最大截面积呈正相关,因此空泡最大截面积越大,球体水下运动时的总流动阻力系数越大。由图23 可知,在空泡闭合后,入水角度越小,空泡最大截面积越大,总流动阻力系数Cd越大。
3 结论
本文结合高速观测技术与数值模拟开展了入水角度对球体入水空泡演化过程影响研究,探讨了球体入水空泡的演化特性,分析了入水角度对入水空泡的影响。主要结论如下:
1)依据球体入水过程中空泡的形态特征,将整个过程分为入水冲击、空泡形成、空泡闭合和空泡溃灭4 个阶段。在入水冲击阶段,球体头部冲击水面,生成对称的水冠;在空泡形成阶段,球体运动挤压水体,在水中形成空泡,空泡在球体的运动下不断被拉长;在空泡闭合阶段,水冠向中间收缩,直至发生面闭合,断开空泡与外界空气的连接,并且空泡在球体拉扯下脱离水面;空泡溃灭阶段,入水空泡尾部以小尺度气泡团的形式泄气溃灭,同时在溃灭夹断处产生回射流,回射流冲击空泡壁面,造成空泡进一步溃灭。
2)球体入水过程中,空泡不断发展,同时整个流场压力也在不断发生明显变化。在入水冲击阶段,球体冲击水面,水体与球体接触区域压力急剧升高,球体受到极大的冲击力导致其速度迅速减小。在空泡形成阶段,空泡内部压力低于水面气压,气体连续流入空泡内部,同时球体头部区域水体的压力比入水冲击时更低。在空泡闭合阶段,喷溅内、外侧压力存在压差,内部较低,外侧较高,在内外压差作用下,喷溅向中间收缩,并实现闭合,且进入空泡的空气流速越高,压力差越大,空泡闭合也越快。在空泡溃灭时,夹断溃灭产生的回射流导致球体速度出现波动。
3)球体入水过程中,入水角度对空泡形态以及球体阻力系数的影响较大,且球体的运动速度和所受冲击载荷因入水角度不同存在较大差异。当球体斜射入水时,产生的水冠不对称。在空泡闭合后,空泡面积随入水角度的增大而减小,拖带着空泡的球体在运动时,总流体阻力系数随入水角度的增大而不断减小。在夹断溃灭阶段,空泡夹断产生的回射流强度随着入水角度的增大而增大。在入水冲击时,随入水角度增大,球体头部压力和其加速度最大绝对值不断增大。

