卷积码盲识别树图遍历算法研究与仿真实验

付卫红，刘乃安，郑靖轩

（西安电子科技大学 通信工程学院，陕西 西安 710071）

0 引言

在现代数字通信系统中，信道编码能够有效地增强信息传输的稳定性和可靠性，但是需要通信双方预先约定好所采用的信道编码，极大地限制了通信系统的灵活性。若接收方能够对发送方所采用的信道编码进行盲识别，则能够在不损害稳定性和可靠性的情况下增加通信系统的灵活性，并提高信道资源的利用率。

卷积码是一种广泛应用于各类场景下的信道编码，对卷积码进行盲识别[1-5]不仅能够提高信道利用率，也能为其他线性信道编码提供新的识别思路。

目前，对于卷积码的盲识别算法主要包括：高斯解方程法、欧几里德算法、Walsh-Hadamard 变换算法等。

高斯解方程法利用卷积码之间的校验关系求解校验矩阵，算法复杂度为O(N3)。文献[6]借助快速合冲算法的理论将高斯解方程的算法复杂度降低到O(N2)。基于快速合冲的编码识别方法的核心思想是Gröbner 基本理论[7-8]，将12 码率卷积码的盲识别问题转化为求解F[x,y]模型中具有良好性质的生成元问题，从而建立起了12 码率卷积码的结构化模型，但该算法只能在无误码情况下完成识别。基于欧几里德算法的编码识别方法[9]则是通过先建立(2,1,m)类卷积码的校验模型，而借助多项式的辗转相除法求得源码的生成矩阵，该方法同样只适用于无误码下的12 卷积码。基于Walsh-Hadamard 变换的卷积码识别算法[10]的原理是根据Hadamard 方阵的元素为各行各列相乘后模2 结果的特征，借助卷积码码字和校验矩阵间的关系，利用Hadamard 矩阵和统计码字向量共同构造Walsh 谱函数，从而求解得到校验矩阵。Walsh-Hadamard 变换法具有较高的抗误码能力，但需要获知编码码率和接收序列起始点。基于对数似然比的卷积码识别算法属于软判决识别算法[11]，其主要思想为：通过对接收序列中包含的可靠度信息进行分析，计算接收序列的后验校验概率的对数似然比，在一定的编码候选集合中，通过计算该集合中各种编码方式的软信息，从而在该集合中寻找到发送端采用的编码方式。该方法仅需利用一段接收序列就可实现编码方式的快速识别，但是需要预先设置一个包含发送端采用的编码方式的封闭集合。

1 卷积码编码原理与盲识别问题

通常用(n,k,m)表示一个卷积码，其中：n代表每个时钟节拍所输出的比特数，又称码长；k代表每个时钟节拍所输入的比特数，又称信息位长度；m代表卷积码生成多项式的最高幂次，又称最大约束长度。卷积码的生成矩阵表示如下：

生成矩阵的每个元素可表示为：

假设输入序列为u=(u0,u1,u2,…,ul-1)，并将其按照每k个比特为一行的方式填充成为一个矩阵，此时将该矩阵的每一列化为多项式形式，得到输入多项式向量u(D)=(u0(D),u1(D),u2(D),…,uk(D))。同 样 地，假设编码输出序列为c=(c0,c1,c2,…,cl-1)，按照每n个比特为一行的方式得到输出多项式向量c(D)=(c0(D),c1(D),c2(D),…,cn(D))。那么根据卷积码的编码原理，有：

将卷积码的校验矩阵记作H(D)，为一个(n-k)×n维矩阵。能够令：

此时由式（3）和式（4）可得：

现有识别算法[12-17]一般通过求解卷积码的校验矩阵来反推出生成矩阵，但对于不同的生成矩阵，校验矩阵可能是相同的。如生成矩阵为：

和

的两个（2,1,2）卷积码，其校验矩阵均可以为：

这说明校验矩阵和生成矩阵并非一一对应的关系。此时，在识别出校验向量后，不能依据校验向量完成生成矩阵识别工作。因此，需要另辟新的方向，以对卷积码进行盲识别。卷积码的盲识别问题可划分为两个子问题：n，k，m三个参数的识别问题；卷积码的生成矩阵识别问题。由于目前对卷积码的n，k，m三个参数的识别已经较为成熟，因此着重讨论对卷积码的生成矩阵盲识别问题。

2 卷积码的树图遍历识别法

2.1 基于树图遍历算法的卷积码输入-状态-输出转移表识别

一般地，可以将卷积码的状态转移用de Bruijn 图进行标识，可以较好地描述卷积码的状态和输出随输入变化而变化的情况。但是de Bruijn 图不能很好地描述卷积码的输入序列，本文采用树图对卷积码进行表示，如图1 所示。

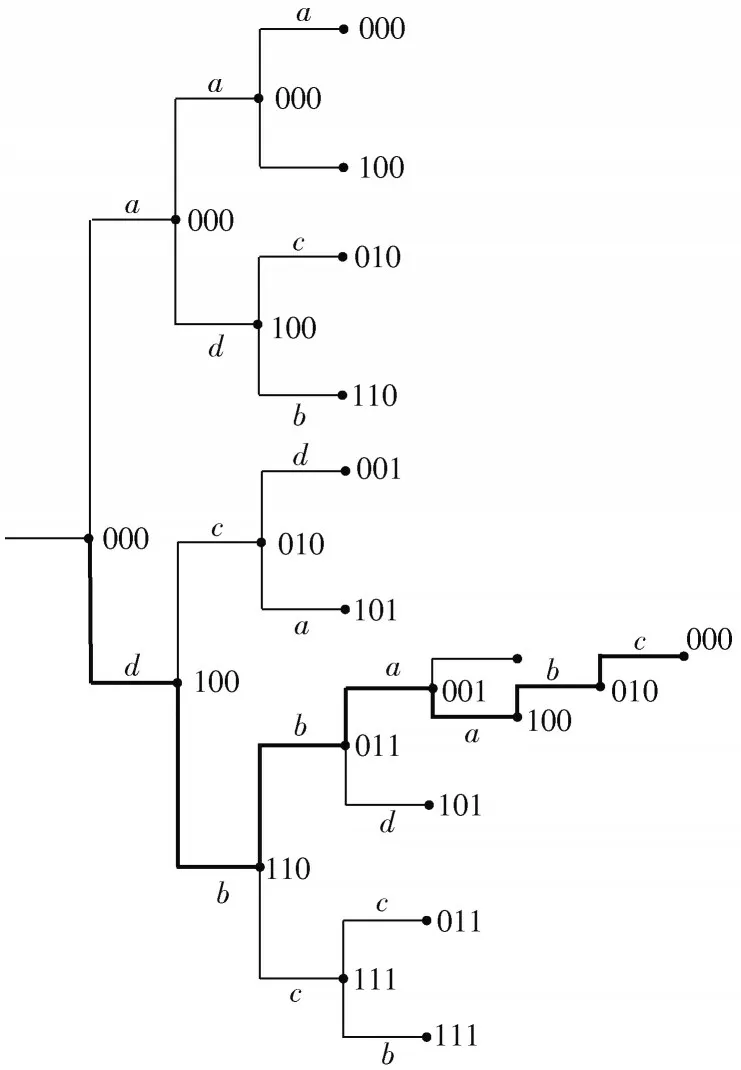
图1 （2，1，3）卷积码的树图表示

卷积码的树图表示中，字母代表输出：a=00，b=01，c=10，d=11；数字代表状态，每个分支向上走代表输入为零，向下走代表输入为1。加粗部分为示例用卷积码的实际路径。用树图表示能够较为完全地表现出卷积码的输入-状态-输出转移情况，对于一个确定的卷积码，这种转移情况是有限的，因此可以将其表示至表1。

表1 输入-状态-输出转移表

对于每一个长度为len 的接收序列，其对应树图中唯一的路径。若输入任意改变一个比特，则路径也随之改变。因此，可以通过已知的接收序列反推输入序列。若采用最大似然的思想，那么应当将当前接收码字译为所有可能输入和状态中后验概率最大的输入和状态。这也是Viterbi 算法[18]的思路。但Viterbi 译码算法需要知道卷积码的生成结构，而这正是本文所要识别的内容。

显然，对于一个(n,k,m) 卷积码，它的每一路输入对应的状态均具有2 种后续状态，对应该路输入比特的2 种可能。当目前输入I和当前状态Sc确定后，卷积码的下一状态Sn也就唯一确定。例如：对于(2,1,3) 卷积码编码器，若当前状态为010，输入为1，则编码器的下一状态必定为101。可以将卷积码结构抽象为两个函数：

那么，第p个输出为：

式中：O(p)表示第p个输出；I(p)表示第p个输入；S0代表初始状态；函数f需要嵌套p层。

由卷积码的编码结构可知：(n,k,m)卷积码中任意一路输入对应的状态转移公式为：

式中gf为反馈向量。非递归卷积码的反馈向量为零，而递归卷积码的反馈向量不为零。

易知，卷积码的状态具有遍历性。记(n,k,m)卷积码在t时刻(t≫m)的第a路输入元素为I(a)(t)，第a路状态为：

由于S(a)(t)具有遍历性，说明本文能够采用递推的方式对卷积码的输入序列进行识别，不必担心一些状态无法被遍历到。此外，对于(n,k,m)卷积码编码器整体而言，每一路输入对应的输入-状态对综合作用才会产生一个输出，具有唯一性。因此，可以利用遍历中产生的冲突来识别卷积码的内部构造，具体思路如下：

1）根据信息位长度和最大约束长度构造转移表，每一行对应一组输入-状态组合。而后，根据当前组合计算出下一状态，填入对应的列中，从零开始遍历初始状态，逐次加1。

此时，将接收序列按每n个比特进行分组，将这n个比特视为一个二进制数字，并将其转化为十进制，得到输出序列；类似地，将输入序列作为全零序列，每k个比特变为一个十进制数字。此外，还可以额外加入一个输出校正序列，其初始状态等于接收序列。

2）开始遍历输入序列和输出校正序列。在转移表中查到当前输入和状态对应的行，在该行中找到“输出”单元格。此时，单元格中的值有三种可能性：空值、等于此时接收值和不等于此时接收值。当为空值和等于此时接收值时，找到下一状态值，并与下一输入值一起重复查表过程；若单元格值等于此时接收值，处理方式与空值时一致；当不等于实际接收值时，情况会相对复杂。

由于在实际通信中，误比特率相对较低，因此优先考虑输入估计错误的问题。当单元格中的值不等于实际接收值时，先令当前输入加1，再重新检查输入-状态组合对应的接收值。全部不符合，那么说明可能出现误比特。

如果出现误比特，则需要根据当前对应的输出值构建候选集，候选集中的元素由与输出值的二进制形式的汉明重量相差1 的二进制数的十进制形式组成。然后，将候选集中的元素作为当前输出值进行遍历，直至出现单元格为空或其值与当前输出值相等为止，将此时的输出值填入输出校正序列中，与输出序列进行比特级的对比，若出现连续两个比特不同，则说明此时的序列估计有误，回退至上一个输入不等于实际接收值状态。若状态一直回退至初始状态，那么初始状态加1 后继续遍历，直至初始状态达到状态的最大值。

3）当遍历完输入序列所有元素后，检查表格是否填充完毕。若填充完毕，则输出转移表，算法结束。

2.2 卷积码的生成矩阵识别算法

用I表示当前输入，Ii表示当前输入左起第i个比特；用S(i)表示当前对应于Ii的状态，表示当前状态左起第j个比特；用O表示当前输出，Oh表示输出的左起第h个比特。那么，可以根据卷积码编码器的结构得到如下关系式：

考虑到卷积码的状态由前序输入唯一决定，即第t时刻的状态由第t-m～t-1 时刻的m个比特的输入构成，即满足：

此时只要识别出矩阵A，即可得到卷积码的生成矩阵。根据识别出的状态转移表即可构造出方程组，以解出矩阵A的各个元素。

3 卷积码盲识别算法仿真实验

在仿真中，利用随机函数构造一个0，1 等概率出现的随机序列，其长度为20 000 bit。对该序列进行编码后得到编码序列。根据编码序列的长度，依照误比特率构造出错误序列，并与编码序列进行比特异或，得到接收序列。将接收序列输入算法进行整体盲识别。每种编码类型在每个误码率下循环1 000 次，统计识别概率。仿真所使用的卷积码如表2 所示。

表2 仿真所使用的卷积码

图2 为本文提出的卷积码盲识别算法对不同形式的卷积码识别结果。从图中可以看出，对于卷积码的4种可能的形式：系统递归卷积码、递归非系统卷积码、系统非递归卷积码和非系统非递归卷积码，本文所提出的算法均能够进行识别和分析。同时，在误比特率为0.01时，算法仍能够保持90%以上的识别正确率，说明算法在工程实践中具有可行性。此外，当误比特率相同时，信息位长度或约束长度越长，则其识别性能越差。原因在于，仿真中采用的接收序列长度是一定的，当码长越长时，接收序列中含有的完整码字就越短，所包含的编码信息就越少。而信息位长度和最大延迟的大小与识别性能呈负相关的原因则是当接收序列长度一定时，本文接收到的接收信息量是一定的，但是信息位长度或最大延迟的值越大，那么需要识别的编码信息就越多，因此会导致识别性能的下降。

图2 本文所提卷积码盲识别算法识别正确率曲线

图3给出了本文所提算法与现有的Walsh-Hadamard算法识别性能对比。可以看到本文所用的算法在误比特率不大于0.01 时，与Walsh-Hadamard 算法的性能相差无几，但在误比特率大于0.01 时，性能弱于原有的Walsh-Hadamard 算法。但是，Walsh-Hadamard 算法具有极高的时间复杂度和空间复杂度，在算法效率上远不及本文提出的基于树图遍历的算法。

图3 卷积码的不同盲识别算法识别正确率曲线

4 结语

本文提出了一种基于树图遍历的卷积码盲识别算法，其原理是遍历卷积码所有可能的初始状态和输入序列，结合卷积码的马尔可夫性，依据接收到的码字序列，不断排除不符合卷积码编码器结构特性的输入序列和初始状态，并最终得到卷积码的输入-状态-输出转移表。之后，根据该表构建方程组，解得卷积码的生成矩阵，完成卷积码的盲识别。最后对算法进行了仿真实验，结果表明，该算法在误比特率为1%时，仍然保持着90%以上的正确率，这说明算法在工程上是可行的。